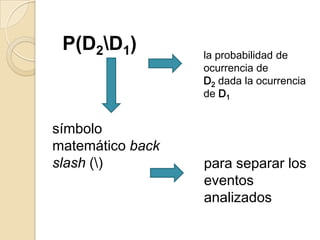
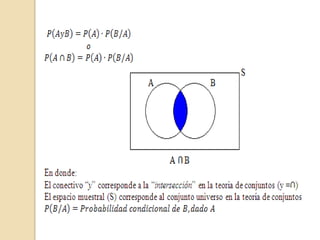
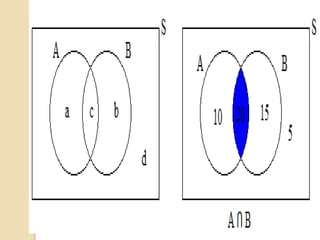
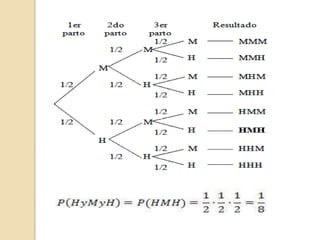
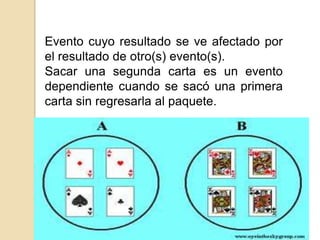
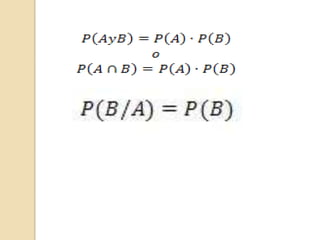Este documento presenta los conceptos de probabilidad condicional, regla de la multiplicación y eventos dependientes e independientes. Explica que la probabilidad condicional calcula la probabilidad de ocurrencia de un evento D2 dado que ocurrió un evento D1. La regla de la multiplicación establece que para eventos independientes la probabilidad conjunta es el producto de las probabilidades individuales, mientras que para eventos dependientes usa la probabilidad condicional. Finalmente, provee ejemplos para ilustrar estas nociones.

1. Presentada por:
Erika Rincón
Andrés Chivata
Leonardo Arroyo
José Gabriel Gómez

2. TEMAS A TRATAR
 Probabilidad Condicional
 Regla de la multiplicación
 Evento dependiente

3. Establece una condición que ha de
cumplirse para que otra sea
verdadera.

4. Para que Sirve??
 justamente sirve para calcular los
chances de ocurrencia de un evento
D2 dada la ocurrencia de un evento
D1, teniendo en cuenta si los eventos
en cuestión son dependientes o
independientes entre sí, y
generalmente este tipo de
probabilidad se expresa mediante la
fórmula

5. P(D2D1)
símbolo
matemático back
slash ()
la probabilidad de
ocurrencia de
D2 dada la ocurrencia
de D1
para separar los
eventos
analizados

6. Ejemplo: se tira un dado y sabemos que la probabilidad
de que salga un 2 es 1/6 (probabilidad a priori). Si
incorporamos nueva información (por ejemplo, alguien
nos dice que el resultado ha sido un número par)
entonces la probabilidad de que el resultado sea el 2 ya
no es 1/6.
Las probabilidades condicionadas se calculan aplicando la
siguiente fórmula:
Donde:
P (B/A) es la probabilidad de que se de el suceso B condicionada a
que se haya dado el suceso A.
P (B A) es la probabilidad del suceso simultáneo de A y de B
P (A) es la probabilidad a priori del suceso A

7. En el ejemplo que hemos visto:
P (B/A) es la probabilidad de que salga el número 2
(suceso B) condicionada a que haya salido un número
par (suceso A).
P (B A) es la probabilidad de que salga el dos y
número par.
P (A) es la probabilidad a priori de que salga un
número par.
Por lo tanto:

8. Ejemplos
Sean A y B dos sucesos aleatorios con p(A) =
1/2, p(B) = 1/3, p(A B)= 1/4. Determinar:
FORMULA:

9. REGLA DE LA
MULTIPLICACION
Si se tienen varios eventos sucesivos
e independientes entre sí, la
probabilidad de que ocurran todos
ellos a la vez corresponde a la
multiplicación de las probabilidades de
cada uno de los eventos.

10. La regla de multiplicación requiere que
dos eventos A y B sean
independientes.
Dos eventos A y B son independientes
si la ocurrencia de una no afecta la
probabilidad de ocurrencia del otro.
La regla especial se escribe: P(A y B) =
P(A) * P(B).

11. Existen dos tipos de regla:
1) Si los eventos de independientes:
P(A y B ) = P( A ∩ B ) = P(A)P(B)
2) Si los eventos son dependientes:
Es la probabilidad de A multiplicada
por la probabilidad condicional de B
dado A.
P(A y B) = P(A)P(B|A)

12. EVENTOS DEPENDIENTES
Si A y B son dos eventos
dependientes, es decir, si la
ocurrencia de A afecta la probabilidad
de ocurrencia de
B, entonces, dicha probabilidad de
calcula empleando la siguiente regla:

14. EJEMPLOS
En una clase de 50 alumnos, 10
alumnos tienen como preferencia
solamente la asignatura
de Matemática, 15 prefieren
solamente Estadística y 5 no tienen
preferencia por ninguna de estas
asignaturas. Calcular la probabilidad que
de un alumno de la clase seleccionado
al azar tenga preferencia por:
Matemática y Estadística.
Estadística y Matemática

16. Datos y cálculos:
a = 10
b = 15
c = S - a - b - d = 50 - 10 - 15 - 5 = 20
d = 5
S = 50
Matemática y Estadística.

17. -Si una moneda equilibrada se lanza dos veces, la
probabilidad de que ambos lanzamientos den por
resultado una “cara” es :
(1/2) x (1/2) = (1/4)
-Chris posee dos inventarios independientes uno de
otro.
La probabilidad de que el inventario A aumente su
valor el próximo año es .5. La probabilidad de que el
B aumente el suyo es .7.
¿Cuál es la probabilidad de que ambos aumenten su
valor el próximo año?
P(A y B) = (.5)(.7) = .35

18. EVENTOS INDEPENDIENTES
Si A y B son dos eventos
independientes, es decir, si
el conocimiento de la incidencia de
uno de ellos no tiene efecto en la
probabilidad de ocurrencia del otro,
entonces, para calcular la probabilidad
de dichos eventos se aplica la
siguiente regla:

20. Una pareja de esposos desean tener 3 hijos.
Suponiendo que las probabilidades de tener un
niño o una niña son iguales, calcular la
probabilidad de éxito en tener hombre en el
primer nacimiento, mujer en el segundo
nacimiento y hombre en el tercer nacimiento.
Solución:
M = mujer
H = hombre
Elaborando un diagrama de árbol se tiene todas
las probabilidades:

22. EVENTO DEPENDIENTE
 Evento cuyo resultado no tiene que ver
con el resultado de otro(s) evento(s).
 Por ejemplo, el resultado de lanzar una
moneda, y que caiga de cualquier
lado, no depende del resultado de
ninguno de los lanzamientos anteriores.
Por lo tanto, cada lanzamiento es un
evento independiente.

24. Evento cuyo resultado se ve afectado por
el resultado de otro(s) evento(s).
Sacar una segunda carta es un evento
dependiente cuando se sacó una primera
carta sin regresarla al paquete.

25. Por definición, A es independiente de B si y
sólo si:A es independiente de B si y sólo si:
(PnA)=P(A)P(B)

26. CONCLUSIONES
Dos (o más) eventos son independientes si la ocurrencia de
un evento no cambia la probabilidad de que otro evento
ocurra. Existen dos tipos de situaciones cuando esto
sucede:
1) Cuando la acción aleatoria no elimina un resultado (como
al lanzar un dado o una moneda varias veces, o realizar
acciones aleatorias que no tienen conexión una con otra
como sacar una carta y luego lanzar un dado); y
2)Cuando la acción aleatoria sí elimina un resultado
posible, pero el resultado es reemplazado antes de que la
acción vuelva a suceder (como sacar una carta y devolverla
al mazo).
3)Cuando los eventos son independientes, la probabilidad
de que todos ocurran es igual a la multiplicación de las
probabilidades de que ocurran los eventos individuales.