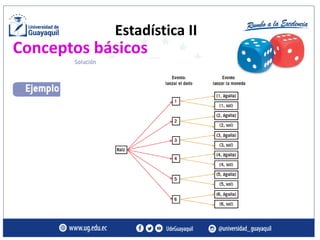
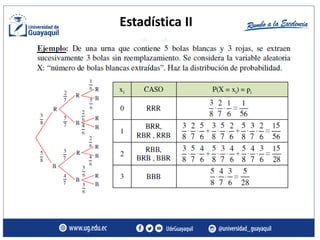
Este documento presenta conceptos básicos de probabilidad y estadística, incluyendo variables aleatorias discretas y continuas. Explica que una variable aleatoria es una función que asocia números reales a los resultados posibles de un experimento aleatorio, y que pueden ser discretas, tomando valores específicos, o continuas, tomando cualquier valor en un rango. También define conceptos como espacio muestral, evento, y función de probabilidad, y proporciona ejemplos de variables aleatorias discretas y continuas.