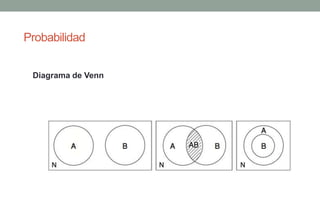
Este documento presenta conceptos básicos de probabilidad. Define probabilidad como la frecuencia relativa de ocurrencia de un evento al repetir un experimento. Explica que un evento es un subconjunto de resultados posibles de un experimento. Describe reglas para calcular la probabilidad de la unión, intersección y complemento de eventos. Finalmente, introduce la noción de probabilidad condicionada como la probabilidad de un evento dado que otro evento ha ocurrido.

1. BIOESTADÍSTICA
Probabilidad
Yerko Bravo; basado en clases de Francisco Javier Barón, Universidad de Málaga

2. • ¿Cuál es la probabilidad de aprobar Bioestadística?
• ¿Cuál es la probabilidad de no encontrarme una congestión
vehicular cuando voy a clase?
• Todos los días nos hacemos preguntas sobre probabilidad e incluso
con lo que se ha visto poco de la materia en cursos anteriores, se
puede tener una idea intuitiva lo suficientemente correcta para lo
que necesitamos de ella en este curso.
• En este tema vamos a:
• Recordar qué entendemos por probabilidad.
• Recordar algunas reglas de cálculo.
Yerko Bravo; basado en clases de Francisco Javier Barón, Universidad de Málaga

3. Nociones de probabilidad
• Hay dos maneras principales de entender la probabilidad:
• Frecuentista (objetiva): Probabilidad de un suceso es la frecuencia
relativa (%) de veces que ocurriría el suceso al realizar un experimento
repetidas veces.
• Subjetiva (bayesiana): Grado de certeza que se posee sobre un suceso.
Es personal.
• En ambos tipos de definiciones aparece el concepto de
suceso o evento. Vamos a recordar qué son y algunas
operaciones que se pueden realizar con sucesos.

4. Sucesos o eventos
• Cuando se realiza un experimento aleatorio diversos resultados son
posibles. El conjunto de todos los resultados posibles se llama E espacio muestral
espacio muestral (E).
• Se llama suceso a un subconjunto de dichos resultados.
• Se llama suceso contrario (complementario) de un suceso A, A’, al
formado por los elementos que no están en A
• Se llama suceso unión de A y B, AUB, al formado por los resultados E espacio muestral
experimentales que están en A o en B (incluyendo los que están en
ambos).
A
• Se llama suceso intersección de A y B, A∩B o simplemente AB, al A’
formado por los resultados experimentales que están
simultáneamente en A y B
E espacio muestral E espacio muestral E espacio muestral
UNIÓN INTERSEC.
A A A
B B B

5. Sucesos o eventos
• Ejemplo:
Una moneda tiene dos lados y cuando se lanza al aire caerá
“cara” o “cruz” pero no ambos.
Un dado tiene seis lados y si se lanza caerá en 1,2,3,4,5 ó 6.
“Cada posible resultado es un evento“.
Ejemplo: dos monedas son lanzadas al aire, hay dos
posibles resultados en cada caso. Por lo tanto, K1= 2 y
K2= 2 y existen (K1) (K2) = (2) (2) = 4 posibles resultados
en el lanzamiento de ambas monedas.

6. Sucesos o eventos
El número de veces para que todas las n cosas ocurran
juntas es
(K1) (K2) (K3) ……….(Kn)
Si tres monedas son lanzadas al aire, cada lanzamiento
resultaría en uno de dos posibles resultados, por lo tanto hay
un total de
(K1) (K2) (K3) = (2) (2) (2) = 8 posibles resultados para los
tres lanzamientos.

7. Teoría de Conjuntos
Conjunto, Elemento, Subconjunto
En un experimento hay un conjunto de posibles resultados:
el Conjunto de Resultados o espacio muestral.
Ejemplo: Lanzar dos monedas.
Conjunto: cuatro elementos = cara, cara; cara, cruz; cruz,
cara; cruz, cruz.
Subconjunto (evento): los lados de un dado = 1,2,3,4,5 ó 6
Intersección: el evento (2,4,6) y el evento (5,6): elemento
común (6).
A (2,4,6) y B (5,6) es A B (6)

8. Teoría de Conjuntos
Mutualmente excluyentes: los eventos números par y
números impar.
Unión de los dos eventos.
A (2,4,6) y B (1,3,5) entonces A B (2,4,6,1,3,5).

9. Probabilidad
La probabilidad es importante para la inferencia estadística.
La probabilidad nos dice qué esperar en términos de
variación de muestra a muestra (cuando se repite un
experimento). Nos ayuda a evaluar la exactitud de nuestra
inferencia.
Evento: colección de posibles resultados de un experimento.
Probabilidad de un evento: frecuencias relativas de la
ocurrencia de ese evento en las repeticiones del
experimento.

10. Probabilidad
Frecuencia relativa:
n° de veces que el evento ocurre/n° de experimentos o,
frecuencia del evento/número total de eventos (f/n).
Ejemplo:

11. Probabilidad
Suma de Probabilidades
Si los eventos son mutuamente excluyentes, la probabilidad de que
ocurra el evento A o el evento B es la suma de las probabilidades de
los dos eventos:
P(A o B) = P(A) + P(B)
Por ejemplo, P(cara o cruz) = P(cara) + P(cruz) = ½ + ½ = 1.
Si los eventos no son mutualmente excluyentes,
P(A o B) = P(A) + P(B) - P(A y B)
Ejemplo lo veremos en clase.

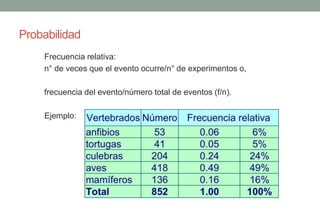
12. Probabilidad
Multiplicación de Probabilidades
Si dos o más eventos se intersectan, la probabilidad asociada con la
intersección es el producto de las probabilidades de los eventos
individuales.
P (A y B) = [P(A)][P(B)]
P (A, B y C) = [P(A)][P(B)] [P(C)]
Por ejemplo, la probabilidad de una moneda salga cara es ½. Si dos
monedas son lanzadas, la probabilidad de que ambas salgan caras es
P (cara, cara) = [P(cara)][P(cara)] = (1/2) (1/2) = (1/4) = 0,25
Donde P (cara,cara) es un resultado de cuatro posibles resultados.

13. Definición de probabilidad
• Se llama probabilidad a cualquier función, P, que asigna a
cada suceso A un valor numérico P(A), verificando las
siguientes reglas (axiomas)
E espacio muestral
• P(E)=1
100%
E espacio muestral
• 0≤P(A) ≤1 A
• P(AUB)=P(A)+P(B) si A∩B=Ø B
• Ø es el conjunto vacío.
• Imaginar la probabilidad de un subconjunto como el tamaño
relativo con respecto al total (suceso seguro)

14. Probabilidad
Multiplicación de Probabilidades
Ejemplo: La tasa de mortalidad por un ataque al corazón en una
unidad coronaria es 15%. (¿cuál es la probabilidad que un paciente
sobreviva?). Otra pregunta: si dos pacientes ingresan a unidad
coronaria en un mismo día y definimos que A es la probabilidad de
que el primer hombre muera y B es la probabilidad de que el
segundo hombre fallezca, ¿Cuál es la probabilidad de que ambos
mueran?

15. Probabilidad
Diagrama de Venn

16. Probabilidad condicionada
Es la probabilidad de ocurrencia de un evento, dado la probabilidad de ocurrencia
de un segundo evento. Es decir que ocurra el primer evento es dependiente de la
ocurrencia del segundo evento.
En estadística, probabilidad de A dado que B ha ocurrido se denomina
probabilidad condicional de A dado B.
Volviendo al Diagrama de Venn
Por lo tanto,

17. Probabilidad condicionada
Si dividimos ambos, numerador y denominador por N, el número total de
todos los posible eventos. Se obtiene:
Por lo tanto…

18. Probabilidad condicionada
• Se llama probabilidad de A condicionada a B, o
probabilidad de A sabiendo que pasa B:
E espacio muestral
P(A Ç B)
P(A | B) = A
P(B) B
 Error frecuentíiiiiiisimo:
 No confundir probabilidad condicionada con intersección.
 En ambos medimos efectivamente la intersección, pero…
 En P(A∩B) con respecto a P(E)=1
 En P(A|B) con respecto a P(B)

19. ¿Qué hemos visto?
• Álgebra de sucesos
• Unión, intersección, complemento
• Probabilidad
• Nociones
• Frecuentista
• Subjetiva o Bayesiana
• Reglas de cálculo
• Complementario, Unión, Intersección
• Algunos ejemplos