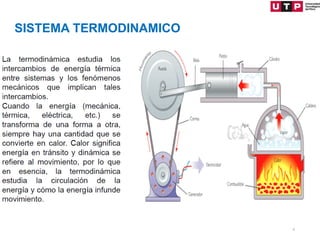
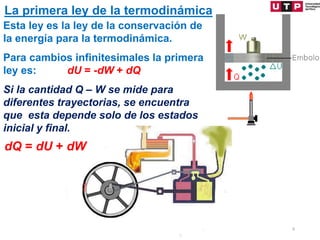
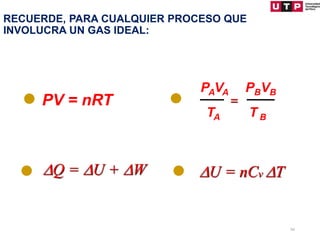
1) El documento describe los conceptos fundamentales de la primera ley de la termodinámica. 2) La primera ley establece que el cambio en la energía interna de un sistema es igual al calor agregado menos el trabajo realizado. 3) Se explican algunas consecuencias de la primera ley como que para un sistema aislado o un proceso cíclico, el cambio en la energía interna es cero.

1. Termodinámica
Primera Ley
Prof. Msc. Ing. Alberto Pacci
1

2. 2
SISTEMA TERMODINAMICO

3. 3
SISTEMA TERMODINAMICO

4. 4
ENERGÍA INTERNA

5. 5

6. 6

7. 7

8. La primera ley de la termodinámica
Esta ley es la ley de la conservación de
la energía para la termodinámica.
Para cambios infinitesimales la primera
ley es: dU = -dW + dQ
Si la cantidad Q – W se mide para
diferentes trayectorias, se encuentra
que esta depende solo de los estados
inicial y final.
8
dQ = dU + dW

9. Consecuencias de la 1a. ley
9
Para un sistema aislado el cambio en la energía interna es
cero.
Puesto que para un sistema aislado Q = W = 0, ΔU = 0.
En un proceso cíclico el cambio
en la energía interna es cero.
En consecuencia el calor Q
agregado al sistema es igual al
trabajo W realizado.
Q = W, ΔU = 0
En un proceso cíclico el trabajo
neto realizado por ciclo es igual al
área encerrada por la trayectoria
que representa el proceso sobre
un diagrama PV.
P
Trabajo = Calor = Área
V
W

10. Aplicaciones de la primera ley
10
Un trabajo es adiabático si no
entra o sale energía térmica del
sistemas, es decir, si Q = 0. En
tal caso: ΔU = - W Expansión libre adiabática
Para la expansión libre adiabática
Q = 0 y W = 0, ΔU = 0
La temperatura de un gas ideal que
sufre una expansión libre permanece
constante.
Como el volumen del gas cambia, la
energía interna debe ser
independiente del volumen, por lo
tanto
Uideal = U(T)
vacío
Gas a Ti
membrana
Muro
aislante
Tf = Ti
membrana

11. LA PRIMERA LEY DE LA
TERMODINÁMICA:
• La entrada neta de calor en un
sistema es igual al cambio en
energía interna del sistema más el
trabajo realizado POR el sistema.
Q = U + W  = (final - inicial)
• Por el contrario, el
trabajo realizado
SOBRE un sistema es
igual al cambio en
energía interna más la
pérdida de calor en el
proceso.
11

12. CONVENCIONES DE SIGNOS
PARA LA PRIMERA LEY
• ENTRADA de calor Q es positiva
Q = U + W  = (final - inicial)
• SALIDA de calor es negativa
• Trabajo POR un gas es positivo
• Trabajo SOBRE un gas es negativo
+Qin
+Wout
+U
-Win
-Qout
−U
12

13. 13
CONVENCIONES DE
SIGNOS PARA LA
PRIMERA LEY

14. APLICACIÓN DE LA PRIMERA LEY
DE LA TERMODINÁMICA
Ejemplo 1: En la figura, el gas absorbe 400 J
de calor y al mismo tiempo realiza 120 J de
trabajo sobre el pistón. ¿Cuál es el cambio en
energía interna del sistema?
14

15. Ejemplo 1: En la figura, el gas absorbe 400 J de calor y al
mismo tiempo realiza 120 J de trabajo sobre el pistón. ¿Cuál
es el cambio en energía interna del sistema?
Q = U + W
Solución
Aplicando la primera ley:
Qin
400 J
Wout =120 J
15
ΔW es positivo: +120 J (trabajo SALE)
Q = U + W U = Q - W
ΔQ es positivo: +400 J (calor ENTRA)
ΔU = Δ Q - Δ W
= (+400 J) - (+120 J)
= +280 J U = +280 J
El aumento en
energía interna es:

16. CUATRO PROCESOS TERMODINÁMICOS:
•Proceso isocórico: ΔV = 0, ΔW = 0
•Proceso isobárico: ΔP = 0
•Proceso isotérmico: ΔT = 0, ΔU = 0
•Proceso adiabático: ΔQ = 0
Q = U + W
16

17. 17

18. CAPACIDAD CALORÍFICA MOLAR
TRATAMIENTO OPCIONAL
La capacidad calorífica molar C se define como al calor
por unidad de mol por grado Celsius.
18
El “mol” es una mejor referencia para gases que el
“kilogramo.” Por tanto, la capacidad calorífica
específica molar se define como:
Por ejemplo, un volumen constante de oxígeno
requiere 21,1 J para elevar la temperatura de un mol
en un grado kelvin.
C =
Q
n T

19. CAPACIDAD CALORÍFICA ESPECÍFICA A
VOLUMEN CONSTANTE
¿Cuánto calor se requiere para
elevar la temperatura de 2
moles de O2 de 0oC a 100oC?
Q = (2 mol)(21,1 J/mol K)(373 K - 273 K)
Q = nCv T
Q = + 4 220 J
19

20. CAPACIDAD CALORÍFICA ESPECÍFICA
A VOLUMEN CONSTANTE (Cont.)
Puesto que el volumen no
cambia, no se realiza trabajo.
Todos los 4 220 J van a aumentar
la energía interna, ΔU.
Q = U = nCv T = 4 220 J
U = nCv T
Por tanto, ΔU se determina
mediante el cambio de temperatura
y el calor específico a volumen
constante.
20

21. CAPACIDAD CALORÍFICA ESPECÍFICA A
PRESIÓN CONSTANTE
Acaba de ver que se necesitaban
4220 J de calor a volumen
constante. Suponga que también
quiere realizar 1000 J de trabajo a
presión constante
Q = U + W
Q = 4 220 J +   J
Q = 5 220 J Cp > Cv
Igual
21

22. CAPACIDAD CALORÍFICA (Cont.)
Cp > Cv
Para presión constante
Q = U + W
nCpT = nCvT + P V
U = nCvT
El calor para elevar la
temperatura de un gas ideal,
ΔU, es el mismo para cualquier
proceso.
Cp
Cv
 =
22

23. 23
MOVIMIENTOS DE UNA PARTÍCULA. EQUIPARTICIÓN DE ENERGÍA

24. 24
MOVIMIENTOS DE UNA PARTÍCULA. EQUIPARTICIÓN DE ENERGÍA

25. 25

26. 26

27. 27
CAPACIDADES CALORIFICAS MOLARES
PARA ALGUNOS GASES

28. 28

29. RECUERDE, PARA CUALQUIER PROCESO QUE
INVOLUCRA UN GAS IDEAL:
PV = nRT
U = nCv T
Q = U + W
PAVA PBVB
TA T B
=
29

30. 30
1. Un gas inicialmente a 300 K se somete a una expansión isobárica a
2,5 kPa. Si el volumen aumenta de 1 m3 a 3 m3, y si 12,5 kJ de energía
se transfieren por calor, calcular:
a) El cambio en la energía interna
b) Su temperatura final.

31. 31
1. Un gas inicialmente a 300 K se somete a una expansión isobárica a
2,5 kPa. Si el volumen aumenta de 1 m3 a 3 m3, y si 12,5 kJ de energía
se transfieren por calor, calcular:
a) El cambio en la energía interna
b) Su temperatura final.
SOLUCIÓN
W = P(Vf – Vi) = 2,5k(3 – 1) = 5 kJ
ΔU = – W + Q = – 5kJ + 12,5 kJ = 7,5 kJ
piVi /Ti = pf Vf /Tf , entonces
Tf = Ti pf Vf /(piVi) = (300)(2,5k)(3)/(2,5k)(1) = 900 K

32. 32
EJERCICIO.- En cierto proceso, 5 moles de gas monoatómico
incrementan su temperatura de 50 hasta 90 °C. Hallar la variación de la
energía interna que experimenta el gas.
SOLUCIÓN

33. 33
EJERCICIO.- En cierto proceso, 5 moles de gas monoatómico
incrementan su temperatura de 50 hasta 90 °C. Hallar la variación de la
energía interna que experimenta el gas.
SOLUCIÓN

34. 34
EJERCICIO.- El diagrama P-V muestra el proceso termodinámico
de cierto gas, del estado 1 donde U1 = 400 J hasta el estado 2
donde U2 = 600 J. Halle el calor suministrado en el proceso 1 → 2.
SOLUCIÓN

35. 35
EJERCICIO.- El diagrama P-V muestra el proceso termodinámico
de cierto gas, del estado 1 donde U1 = 400 J hasta el estado 2
donde U2 = 600 J. Halle el calor suministrado en el proceso 1 → 2.
SOLUCIÓN

36. 36
EJERCICIO.- En el diagrama P-V se representa el proceso
termodinámico de cierto gas. La energía interna en A es 10 J,
encuentre la energía interna en C sabiendo que el calor
suministrado en el proceso A - B - C es 120 J.
SOLUCIÓN

37. 37
EJERCICIO.- En el diagrama P-V se representa el proceso
termodinámico de cierto gas. La energía interna en A es 10 J,
encuentre la energía interna en C sabiendo que el calor
suministrado en el proceso A - B - C es 120 J.
SOLUCIÓN

38. 38
EJERCICIO.- En el diagrama P-V se muestra el proceso de 1 a
2 de un gas ideal cuando recibe 900 J de energía calorífica. Encuentre
el incremento de su energía interna.
SOLUCIÓN

39. 39
EJERCICIO.- En el diagrama P-V se muestra el proceso de 1 a
2 de un gas ideal cuando recibe 900 J de energía calorífica. Encuentre
el incremento de su energía interna.
SOLUCIÓN

40. 40
EJERCICIO.- Un gas ideal experimenta un proceso a presión
constante (P = 2 x 105 N/m2) desde un volumen inicial de 1 litro hasta
un volumen final de 5 litros. Si el calor transferido es 1 kJ, halle la
variación de la energía interna que experimenta el gas.
SOLUCIÓN

41. 41
EJERCICIO.- Un gas ideal experimenta un proceso a presión
constante (P = 2 x 105 N/m2) desde un volumen inicial de 1 litro hasta
un volumen final de 5 litros. Si el calor transferido es 1 kJ, halle la
variación de la energía interna que experimenta el gas.
SOLUCIÓN

42. 42
EJERCICIO.- En un diagrama P-V se muestra un proceso A -B -C,
donde AB: isócoro y BC: isobárico, de 3 mol de cierto gas
monoatómico. Hallar la cantidad de calor suministrado en todo el
proceso. CV = 3 cal/mol.K y CP = 5 cal/mol.K
SOLUCIÓN

43. 43
EJERCICIO.- En un diagrama P-V se muestra un proceso A -B -C,
donde AB: isócoro y BC: isobárico, de 3 mol de cierto gas
monoatómico. Hallar la cantidad de calor suministrado en todo el
proceso. CV = 3 cal/mol.K y CP = 5 cal/mol.K
SOLUCIÓN

44. 44
EJERCICIO.- En el diagrama P-V se muestra dos procesos. En
el proceso C1 se suministra 400 J y el gas ideal realiza un trabajo
de 150 J. Halle el calor suministrado en el proceso C2 sabiendo
que el gas realizó un trabajo de 120 J en dicho proceso.
SOLUCIÓN

45. 45
EJERCICIO.- En el diagrama P-V se muestra dos procesos. En
el proceso C1 se suministra 400 J y el gas ideal realiza un trabajo
de 150 J. Halle el calor suministrado en el proceso C2 sabiendo
que el gas realizó un trabajo de 120 J en dicho proceso.
SOLUCIÓN

46. 46
EJERCICIO.- En el sistema termodinámico mostrado se produce
un proceso isotérmico (T = constante). El pistón desciende 0,5 m.
Hallar el calor disipado al medio ambiente. El bloque tiene una
masa M = 400 kg y desprecie el peso del pistón, (g = 10 N/kg)
SOLUCIÓN

47. 47
EJERCICIO.- En el sistema termodinámico mostrado se produce
un proceso isotérmico (T = constante). El pistón desciende 0,5 m.
Hallar el calor disipado al medio ambiente. El bloque tiene una
masa M = 400 kg y desprecie el peso del pistón, (g = 10 N/kg)
SOLUCIÓN

48. 48
EJERCICIO.- Un sistema termodinámico evoluciona desde un
estado (1), P1 = 10 kN/m2; V1 = 2 m3, hasta un estado (2); V2 = 8 m3,
isobáricamente. Si recibe una cantidad de calor: Q = 100 kJ, hallar
el cambio de energía interna del sistema.)
SOLUCIÓN

49. 49
EJERCICIO.- Un sistema termodinámico evoluciona desde un
estado (1), P1 = 10 kN/m2; V1 = 2 m3, hasta un estado (2); V2 = 8 m3,
isobáricamente. Si recibe una cantidad de calor: Q = 100 kJ, hallar
el cambio de energía interna del sistema.)
SOLUCIÓN

50. 50
EJERCICIO.- Un sistema termodinámico realiza un proceso isocoro
(V = constante) obteniendo calor de una resistencia eléctrica R =
20 Ω por el cual circula una corriente i = 10 amperes, durante 1
minuto. Hallar la variación de la energía interna del sistema.
SOLUCIÓN

51. 51
EJERCICIO.- Un sistema termodinámico realiza un proceso isocoro
(V = constante) obteniendo calor de una resistencia eléctrica R =
20 Ω por el cual circula una corriente i = 10 amperes, durante 1
minuto. Hallar la variación de la energía interna del sistema.
SOLUCIÓN

52. 52
EJERCICIO.- La figura representa en el diagrama P-V el ciclo
experimentado por un gas ideal. La energía interna en A es de 10 J
y en B es 15 J.
a) ¿Cuál es el trabajo efectuado por el gas de A a B?
b) ¿Cuál es el calor suministrado al gas de A a B?
c) ¿Cuál es el trabajo realizado por el gas de C a A?
d) ¿Cuál es el trabajo efectuado por el gas en este ciclo?
SOLUCIÓN

53. 53
EJERCICIO.- La figura representa en el
diagrama P-V el ciclo experimentado por
un gas ideal. La energía interna en A es
de 10 J y en B es 15 J.
a) ¿Cuál es el trabajo efectuado por el
gas de A a B?
b) ¿Cuál es el calor suministrado al
gas de A a B?
c) ¿Cuál es el trabajo realizado por el
gas de C a A?
d) ¿Cuál es el trabajo efectuado por el
gas en este ciclo?
SOLUCIÓN

54. 54

55. 55
2. Un gas se comprime a presión constante de 0,800 atm de 9,00 L a
2,00 L. En el proceso salen 400 J de energía de gas por calor,
a) ¿Cuál es el trabajo efectuado por el gas?
b) ¿Cuál es el cambio en su energía interna?
SOLUCIÓN

56. 56
2. Un gas se comprime a presión constante de 0,800 atm de 9,00 L a
2,00 L. En el proceso salen 400 J de energía de gas por calor,
a) ¿Cuál es el trabajo efectuado por el gas?
b) ¿Cuál es el cambio en su energía interna?
SOLUCIÓN
Q = - 400 J
a) W = P.(V2-V1) = 0,8 atm.(2-9)L
W = 0,8x101325 Pa(-7) x10-3m3
W= - 567,42 J
b) ΔU = Q - W
ΔU= - 400 – (-567,42)
ΔU= 167,42 J

57. Problemas propuestos
57
1. Una bala de plomo de 45 g, que viaja a 200 m/s, se
detiene en un blanco, ¿Cuánto aumentará la
temperatura del plomo si el 80% de la energía se emplea
en calentarlo? La masa de 1 mol de Pb es 208 g.
2. Un trozo de cobre de 100 g se calienta de 0°C hasta
100°C, a la presión atmosférica. ¿Cuál es el cambio de
su energía interna?
3. El gas de un cilindro se deja expandir desde un
volumen de 1,0 x 10–3 m3 hasta uno de 2,5 x 10–3 m3 y, al
mismo tiempo, la presión varía linealmente con
respecto al volumen, desde 1,3 atm iniciales, hasta una
presión final de 0,85 atm. ¿Cuál es el trabajo efectuado
por el gas?
4. Se llevan tres moles de gas por un ciclo termodinámico
de la figura. El ciclo consta de 1) una expansión
isotérmica de A → B a una temperatura de 400K, y una
presión pA = 6,5 atm; 2) una compresión isobárica de B
→ C a 1 atm; y 3) un aumento isocórico de presión C →
A. ¿Qué trabajo se efectúa sobre el gas por ciclo?
6,5
1
T = 400K
A
B
C
p
V

58. Q = 0
EJERCICIO: Un gas diatómico a 300 K y 1 atm se comprime
adiabáticamente, lo que disminuye su volumen por 1/12. (VA
= 12VB). ¿Cuáles son la nueva presión y temperatura? ( =
1,4)
58
SOLUCIÓN

59. Q = 0
A
B
PB
VB VA
PA
PAVA PBVB
TA T B
=
PAVA = PBVB
 
EJERCICIO: Un gas diatómico a 300 K y 1 atm se comprime
adiabáticamente, lo que disminuye su volumen por 1/12. (VA
= 12VB). ¿Cuáles son la nueva presión y temperatura? ( =
1,4)
59
SOLUCIÓN

60. Cálculo de PB
Q = 0
PB = 32,4 atm
o 3 284 kPa
1.4
12 B
B A
B
V
P P
V
 
=  
 
1.4
(1 atm)(12)
B
P =
PAVA = PBVB
 
A
B
PB
VB 12VB
1 atm
300 K Resolver para PB:
A
B A
B
V
P P
V

 
=  
 
60

61. Cálculo de TB
Q = 0
TB = 810 K
(1 atm)(12VB) (32,4 atm)(1 VB)
(300 K) T B
=
A
B
32,4 atm
VB 12VB
1 atm
300 K
Resuelva para TB
TB=?
A A B B
A B
P V P V
T T
=
61

62. Continuación: Si VA= 96 cm3 y VB= 8 cm3,
calcular W
Q = 0
62

63. Continuación: Si VA= 96 cm3 y VB= 8 cm3,
calcular W
Q = 0
W = - U = - nCV T y CV= 21,1 j/mol K
A
B
32,4 atm
1 atm
300 K
810 K
Dado que
Q = 0,
W = - U
8 cm3 96 cm3
Encuentre n
del punto A
PV = nRT
PV
RT
n =
63

64. (Cont.): Si VA = 96 cm3 y VB = 8 cm3,
Calcular ΔW
A
B
32,4 atm
1 atm
300 K
810 K
8 cm3 96 cm3
PV
RT
n = =
(101 300 Pa)(96 x10-6 m3)
(8,314 J/mol K)(300 K)
n = 0,00384 mol y CV= 21,1 j/mol K
T = 810 - 300 = 510 K
W = - U = - nCV T
W = - 41,3 J
64

65. Problema ejemplo:
• AB: se calienta a V constante a 400 K.
Una muestra de 2 L de gas oxígeno tiene
temperatura y presión iniciales de 200 K y 1 atm. El
gas experimenta cuatro procesos:
• BC: se calienta a P constante a 800 K.
• CD: se enfría a V constante de vuelta a 1 atm.
• DA: se enfría a P constante de vuelta a 200 K.
Completar la siguiente tabla:
65
B
A
PB
2 L
1 atm
200 K
400 K 800 K
C
D

66. DIAGRAMA PV PARA PROBLEMA
B
A
PB
2 L
1 atm
200 K
400 K 800 K
¿Cuántas moles
de O2 hay
presentes?
Considere el punto
A:
PV = nRT
66

67. PROCESO AB: ISOCÓRICO
¿Cuál es la presión
en el punto B?
PA PB
TA T B
=
1 atm PB
200 K 400 K
=
PB = 2 atm
ó 203 kPa
B
A
PB
2 L
1 atm
200 K
400 K 800 K
67

68. PROCESO AB: Q = U + W
Analice la primera
ley para el proceso
ISOCÓRICO AB.
W = 0
Q = U = nCv T
U = (0,122 mol)(21,1 J/mol K)(400 K - 200 K)
B
A
PB
2 L
1 atm
200 K
400 K 800 K
Q = +514 J W = 0
U = +514 J
68

69. PROCESO BC: ISOBÁRICO
¿Cuál es el
volumen en el
punto C (y D)?
VB V C
TB T C
=
2 L V C
400 K 800 K
=
B
C
PB
2 L
1 atm
200 K
400 K 800 K
D
4 L
V C = V D = 4 L
69

70. ENCUENTRE ΔU PARA EL
PROCESO BC.
El proceso BC es
ISOBÁRICO.
P = 0
U = nCv T
U = (0,122 mol)(21,1 J/mol K)(800 K - 400 K)
U = +1028 J
B
C
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
70

71. ENCUENTRAR ΔW PARA EL PROCESO BC:
El trabajo
depende del
cambio en V.
P = 0
Trabajo = PV
ΔW = (2 atm)(4 L - 2 L) = 4 atm L = 405 J
W = +405 J
B
C
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
71

72. ENCUENTRE ΔQ PARA EL
PROCESO BC.
Analice la
primera ley para
BC.
Q = U + W
Q = +1028 J + 405 J
Q = +1433 J
Q = 1433 J W = +405 J
B
C
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
U = 1028 J
72

73. PROCESO CD: ISOCÓRICO
¿Cuál es la
temperatura en el
punto D?
PC PD
TC T D
=
2 atm 1 atm
800 K TD
= T D = 400 K
B
A
PB
2 L
1 atm
200 K
400 K 800 K
C
D
73

74. PROCESO CD: ΔQ = ΔU + ΔW
Analice la
primera ley para
el proceso
ISOCÓRICO CD.
W = 0
Q = U = nCv T
U = (0,122 mol)(21,1 J/mol K)(400 K - 800 K)
Q = -1 028 J W = 0
U = -1 028 J
C
D
PB
2 L
1 atm
200 K
400 K 800 K
400 K
74

75. ENCUENTRE ΔU PARA EL PROCESO DA
El proceso DA
es ISOBÁRICO.
P = 0
U = nCv T
U = (0,122 mol)(21,1 J/mol K)(200 K - 400 K)
U = - 514 J
A
D
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
400 K
75

76. ENCUENTRE ΔW PARA EL
PROCESO DA
El trabajo
depende del
cambio en V.
P = 0
Trabajo = PV
W = (1 atm)(2 L - 4 L) = - 2 atm L = - 203 J
W = - 203 J
A
D
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
400 K
76

77. ENCUENTRE ΔQ PARA EL
PROCESO DA
Analice la primera
ley para DA.
Q = U + W
Q = -514 J - 203 J
Q = -717 J
Q = -717 J W = -203 J
U = -514 J
A
D
2 L
1 atm
200 K
400 K 800 K
4 L
2 atm
400 K
77

78. RESUMEN DEL PROBLEMA
Q = U + W
Para todos
los
procesos:
Proceso Q U W
AB 514 J 514 J 0
BC 1433 J 1028 J 405 J
CD -1028 J -1028 J 0
DA -717 J -514 J -203 J
Total 202 J 0 202 J
78

79. TRABAJO NETO PARA CICLOS
COMPLETOS ES ÁREA ENCERRADA
B C
2 L
1 atm
4 L
2 atm
+404 J B C
2 L
1 atm
4 L
2 atm
-202 J
área = (1 atm)(2 L)
trabajo neto = 2 atm L = 202 J
2 L 4 L
B C
1 atm
2 atm
79

80. 80
ENTALPÍA

81. 81
ENTALPÍA

82. •Absorbe calor Qhot
•Realiza trabajo Wout
•Liberación de calor Qcold
Una máquina térmica
es cualquier
dispositivo que pasa
por un proceso cíclico:
Dep. frío TC
Máquina
Dep. Caliente TH
Qhot
Wout
Qcold
MÁQUINAS TÉRMICAS
82

83. 83

84. LA SEGUNDA LEY DE LA
TERMODINÁMICA
Es imposible construir una
máquina que, al operar en
un ciclo, no produzca
efectos distintos a la
extracción de calor de un
depósito y la realización de
una cantidad equivalente de
trabajo.
No sólo no puede ganar (1a ley); ¡ni siquiera
puede empatar (2a ley)!
Wout
Dep. frío TC
Máquina
Dep. caliente TH
Qhot
Qcold
84

85. LA SEGUNDA LEY DE LA
TERMODINÁMICA
Dep. frío TC
Máquina
Dep. caliente TH
400 J
300 J
100 J
• Máquina posible. • Máquina
IMPOSIBLE.
Dep. frío TC
Máquina
Dep. caliente TH
400 J
400 J
85

86. EFICIENCIA DE UNA MÁQUINA
Dep. frío TC
Máquina
Dep. caliente TH
QH W
QC
La eficiencia de una máquina
térmica es la razón del
trabajo neto realizado W a la
entrada de calor QH.
e = 1 -
QC
QH
e = =
W
QH
QH- QC
QH
86

87. EJEMPLO DE EFICIENCIA
Dep. frío TC
Máquin
a
Dep. caliente TH
800 J W
600 J
Una máquina absorbe 800 J
y desecha 600 J cada ciclo.
¿Cuál es la eficiencia?
e = 1 -
600 J
800 J
e = 1 -
QC
QH
e = 25%
Pregunta: ¿Cuántos joules de trabajo se
realizan?
87

88. EFICIENCIA DE UNA MÁQUINA
IDEAL (máquina de Carnot)
Para una máquina perfecta, las
cantidades Q de calor ganado y
perdido son proporcionales a
las temperaturas absolutas T.
e = 1 -
TC
TH
e =
TH- TC
TH
Dep. frío TC
Máquina
Dep. caliente TH
QH W
QC
88

89. Ejemplo 3: Una máquina de vapor absorbe 600 J
de calor a 500 K y la temperatura de escape es 300
K. Si la eficiencia real sólo es la mitad de la
eficiencia ideal, ¿cuánto trabajo se realiza durante
cada ciclo?
e = 1 -
TC
TH
e = 1 -
300 K
500 K
e = 40%
e real = 0,5 ei = 20%
e =
W
QH
W = e QH = 0,20 (600 J)
Trabajo = 120 J
89

90. GRACIAS POR SU
ATENCIÓN
90