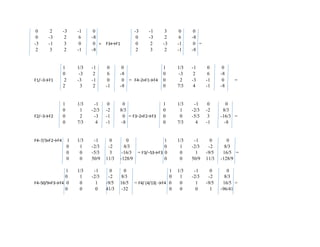
El documento presenta 5 ejercicios de álgebra lineal resueltos por un estudiante. El primer ejercicio pide dar un ejemplo de sistemas de ecuaciones lineales equivalentes con distinto número de ecuaciones. El segundo ejercicio resuelve un sistema de 4 ecuaciones y 4 incógnitas mediante el método de Gauss-Jordán. El tercer ejercicio aplica la eliminación gaussiana modificada a una matriz. El cuarto ejercicio determina el rango y columnas básicas de una matriz. El quinto ejercicio determina si un sistema

1. INSTITUTO UNIVERSITARIO POLITÉCNICO “SANTIAGO MARIÑO”
EXTENSION BARINAS
CATEDRA: Análisis Numérico
ACTIVIDAD 4
Resolver los ejercicios dados. Identifica con tu nombre, cedula y graba en formato Word o
pdf. (Ponderación 15 puntos, 3 cada puntos cada ejercicio) , debes ser organizado en
presentación de la resolución , especificar cada paso que hagas.
Nombre: JOSE CAMEJO
Cedula: 21.022.444
1. Dar un ejemplo de dos sistemas de ecuaciones lineales equivalentes con distinto
número de Ecuaciones.
Solución:
Para discutir un sistema de ecuaciones lineales, determinamos los rangos de la matriz
de coeficientes y de la ampliada y aplicamos el teorema de Rouché.
Puesto que det(A) = -64, podemos afirmar que el rango de A es 3 y la matriz ampliada,
al no poder superar este rango, también resulta de rango 3. Como coincide con el
número de incógnitas, el sistema es compatible determinado.
Para resolverlo, como es compatible determinado, podemos aplicar los dos métodos
indicados anteriormente:
Si calculamos la inversa de A, obtenemos:
Luego la solución del sistema es:

2. Es decir, x=-3, y=1, z=2.
Solución
En este caso el número de ecuaciones es mayor que el número de incógnitas, por lo que
sobra alguna ecuación y por lo tanto hemos de eliminarla del sistema.
Pero ¿cuántasy cuáles eliminamos? La respuesta viene dadopor el rangode las matrices
de coeficientes y ampliada: Si el sistema tiene solución nos quedaremos con un número
de ecuaciones igual al rango de la matriz de coeficientes: cuantas. Las que nos
quedaremos serán aquellas que han dado lugar al rango, es decir, las que sean
independientes: cuales.
En nuestro caso, de las cuatro ecuaciones sólo dos son independientes (luego hemos de
eliminar otras dos). Como el rango de la matriz formada por los coeficientes de las dos
primeras ecuaciones es 2 entonces nos quedamos con las dos primeras ecuaciones.
El sistema queda entonces:
Sistema compatible e indeterminado cuyas infinitas soluciones vienen dadas:
2. Resuelva por Gauss Jordán el siguiente sistema de ecuaciones Lineales

4. 0 2 -3 -1 0 -3 -1 3 0 0
0 -3 2 6 -8 0 -3 2 6 -8
-3 -1 3 0 0 = F3↔F1 0 2 -3 -1 0 =
2 3 2 -1 -8 2 3 2 -1 -8
1 1/3 -1 0 0 1 1/3 -1 0 0
0 -3 2 6 -8 0 -3 2 6 -8
F1/−3→F1 2 -3 -1 0 0 = F4−2×F1→F4 0 2 -3 -1 0 =
2 3 2 -1 -8 0 7/3 4 -1 -8
1 1/3 -1 0 0 1 1/3 -1 0 0
0 1 -2/3 -2 8/3 0 1 -2/3 -2 8/3
F2/−3→F2 0 2 -3 -1 0 = F3−2×F2→F3 0 0 -5/3 3 -16/3 =
0 7/3 4 -1 -8 0 7/3 4 -1 -8
F4−7/3×F2→F4 1 1/3 -1 0 0 1 1/3 -1 0 0
0 1 -2/3 -2 8/3 0 1 -2/3 -2 8/3
0 0 -5/3 3 -16/3 = F3/−53→F3 0 0 1 -9/5 16/5 =
0 0 50/9 11/3 -128/9 0 0 50/9 11/3 -128/9
1 1/3 -1 0 0 1 1/3 -1 0 0
0 1 -2/3 -2 8/3 0 1 -2/3 -2 8/3
F4−50/9×F3→F4 0 0 1 -9/5 16/5 = F4/ (4/13) →F4 0 0 1 -9/5 16/5 =
0 0 0 41/3 -32 0 0 0 1 -96/41

5. F3−(−9/5) F4→F3 1 1/3 -1 0 0 F2−(−2) F4→F2 1 1/3 -1 0 0
0 1 -2/3 -2 8/3 0 1 -2/3 0 -248/12
0 0 1 0 -208/205 = 0 0 1 0 -208/205 =
0 0 0 1 -96/41 0 0 0 1 -96/41
F2−(−2/3)F3→F2 1 1/3 -1 0 0 F1−(−1) F3→F1 1 1/3 0 0 -208/205
0 1 0 0 -552/205 0 1 0 0 -552/205
0 0 1 0 -208/205 = 0 0 1 0 -208/205
0 0 0 1 -96/41 0 0 0 1 -96/41
F1(−1/3) F2→F1 1 0 0 0 -24/205
0 1 0 0 -552/205
0 0 1 0 -208/205
0 0 0 1 -96/41
 De la ecuación 4 del sistema (1) encontramos con la variable x4:
x4=−96/41
 De la ecuación 3 del sistema (1) encontramos con la variable x3:
x3=−208/205
 De la ecuación 2 del sistema (1) encontramos con la variable x2:
x2=−552/205

6.  De la ecuación 1 del sistema (1) encontramos con la variable x1:
x1=−24/205
La respuesta:
 x1=−24/205
 x2=−552/205
 x3=−208/205
 x4=−96/41

7. 3. Aplicar la eliminación Gaussiana modificada a la Matriz dada
1 2 1 3 3
2 4 0 4 4
1 2 3 5 5
2 4 0 4 7
X1 X2 X3 X4 b
1 1 2 1 3 3
2 2 4 0 4 4
3 1 2 3 5 5
4 2 4 0 4 7
Encuentra el pivote en la columna número 1 en la fila número 1
X1 X2 X3 X4 b
1 1 2 1 3 3
2 2 4 0 4 4
3 1 2 3 5 5
4 2 4 0 4 7
Multiplica la fila numero 1 por 2
X1 X2 X3 X4 b
1 2 4 2 6 6
2 2 4 0 4 4
3 1 2 3 5 5
4 2 4 0 4 7

8. Sustrae la fila numero 1 de la fila numero 2 y restaurarla
X1 X2 X3 X4 b
1 1 2 1 3 3
2 0 0 -2 -2 -2
3 1 2 3 5 5
4 2 4 0 4 7
Resta la fila numero 1 por la fila numero 3
X1 X2 X3 X4 b
1 1 2 1 3 3
2 0 0 -2 -2 -2
3 0 0 2 2 2
4 2 4 0 4 7
Multiplica la fila numero 1 por 2
X1 X2 X3 X4 b
1 2 4 2 6 6
2 0 0 -2 -2 -2
3 0 0 2 2 2
4 2 4 0 4 7
Sustrae la fila numero 1 de la fila numero 4 y restaurarla
X1 X2 X3 X4 b

9. 1 1 2 1 3 3
2 0 0 -2 -2 -2
3 0 0 2 2 2
4 0 0 -2 -2 1
Encuentra el pivote en la columna número 3 dividiendo la fila número 2 entre -2
X1 X2 X3 X4 b
1 1 2 1 3 3
2 0 0 1 1 1
3 0 0 2 2 2
4 0 0 -2 -2 1
Resta la fila numero 2 por la fila numero 1
X1 X2 X3 X4 b
1 1 2 0 2 2
2 0 0 1 1 1
3 0 0 2 2 2
4 0 0 -2 -2 1
Multiplica la fila numero 2 por 2
X1 X2 X3 X4 b
1 1 2 0 2 2
2 0 0 2 2 2

10. 3 0 0 2 2 2
4 0 0 -2 -2 1
Resta la fila numero 2 por la fila numero 3
X1 X2 X3 X4 b
1 1 2 0 2 2
2 0 0 2 2 2
3 0 0 0 0 0
4 0 0 -2 -2 1
Multiplicar la fila numero 2 por -1
X1 X2 X3 X4 b
1 1 2 0 2 2
2 0 0 -2 -2 -2
3 0 0 0 0 0
4 0 0 -2 -2 1
Sustrae la fila numero 2 de la fila numero 4 y restaurarla
X1 X2 X3 X4 b
1 1 2 0 2 2
2 0 0 1 1 1
3 0 0 0 0 0
4 0 0 0 0 3
El sistema es inconsistente

11. 4. Determine el Rango y columnas básicas del siguiente Matriz
1 2 1 2
2 4 3 1
3 1 2 4
Solución:
1 2 1 2
2 4 3 1
3 1 2 4
de 2; 3 filas sustraigamos la1 línea, multiplicada respectivamente por 2; 3
1 2 1 2
0 0 1 -3
0 -5 -1 -2
cambiemos de lugares 2-ésimo y3-ésimo
1 2 1 2
0 -5 -1 -2
0 0 1 -3
Dividamos 2-ésimo por -5
1 2 1 2
0 1 0.2 0.4
0 0 1 -3
de 1 filas sustraigamos la 2 línea, multiplicadarespectivamente por 2
1 0 0.6 1.2
0 1 0.2 0.4
0 0 1 -3
de 1; 2 filas sustraigamos la3 línea, multiplicada respectivamente por 0.6;0.2
1 0 0 3
0 1 0 1
0 0 1 -3
Resultado. Calcular el rango de una matriz. Así que hay 3 filas no nulas,
entonces Rank(A) = 3.

12. 5. Determine si el sistema es compatible