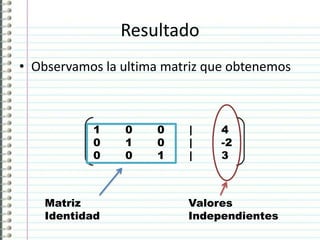
El método de Gauss-Jordán permite resolver sistemas de ecuaciones lineales y encontrar matrices inversas. Se convierte el sistema en una matriz aumentada y luego se aplican transformaciones como multiplicar filas por escalares y sumar/restar filas para convertirla en una matriz identidad, cuya solución proporciona los valores de las incógnitas o la matriz inversa original.

1. Eliminación de
Gauss-Jordán
Por:
Hernández Castillo Leo Zuriel
Salinas Villaseñor Cesar Ivan

2. Definición
• - El Método de Gauss – Jordán o también
llamado eliminación de Gauss – Jordán, es un
método por el cual pueden resolverse
sistemas de ecuaciones lineales con n
números de variables, encontrar matrices y
matrices inversas

3. Resolver sistema de ecuaciones
por el método de Gauss - Jordán

4. • Antes de resolver el sistema de
ecuaciones, hay que convertirlo a una “Matriz
Aumentada” que es la que se obtiene al
combinar dos matrices (o un sistema de
ecuaciones y sus resultados), tal y como se
muestra aquí:

5. Transformaciones Básicas
• Existen 3 reglas o “pasos” que nos pueden
ayudar a resolver las matrices aumentadas, y
convertirlas en identidad:
• Multiplicar o dividir filas por escalares
Fi  (c)Fi
• Sumar o restar filas
Fj  Fj + (c)Fi
• Intercambiar filas entre ellas
Fi   Fj

6. Resolución de una Eliminación de
Gauss – Jordán (paso a paso)

7. Resolver
el sistema de ecuaciones:
-2x +4y +6z = 18
4x+5y +6z = 24
3x + y -2z = 4

8. Paso 1
• Primero, hay que pasar el sistema de
ecuaciones a una matriz aumentada
2x +4y +6z = 18
4x +5y +6z = 24
3x + y -2z = 4
2 4 6 | 18
4 5 6 | 24
3 1 -2 | 4

9. Paso 2
• Dividir la primer fila para hacer el coeficiente
de X = 1
F1  (1/2)F1
1 2 3 | 9
4 5 6 | 24
3 1 -2 | 4

10. Paso 3
• Eliminar los términos de X de las demás filas;
multiplicando la primera fila por los números
adecuados y sumándola/restándola a la segunda y
tercer fila
F2  F2 – (4)F1
F3  F3 – (3)F1
1 2 3 | 9
0 -3 -6 | -12
0 -5 -11 | -23

11. Paso 4
• Dividimos la segunda fila para hacer el
coeficiente de Y = 1
F2  (-1/3)F2
1 2 3 | 9
0 1 2 | 4
0 -5 -11 | -23

12. Paso 5
• Hacemos 0 los coeficientes de Y en las filas 1 y
3
F1  F1 – (2)F2
F3  F3 – (5)F2
1 0 -1 | 1
0 1 2 | 4
0 0 -1 | -3

13. Paso 6
• Multiplicamos la tercer fila para hacer el
coeficiente de Z igual a 1
F3  (-1)F3
1 0 -1 | 1
0 1 2 | 4
0 0 1 | 3

14. Paso 7
• Hacemos 0 los coeficientes de Z en las filas 1 y
2
F1  F1 + F3
F2  F2 – (2)F3
1 0 0 | 4
0 1 0 | -2
0 0 1 | 3

15. Resultado
• Observamos la ultima matriz que obtenemos
Matriz
Identidad
Valores
Independientes

16. Solución
“X” “Y” “Z”
Ecuación 1 1 0 0 | 4
Ecuación 2 0 1 0 | -2
Ecuación 3 0 0 1 | 3
“X” = 4
“Y” = -2
“Z” = 3
Solución:

17. Resolución de una Inversa con
Gauss- Jordán (Paso a Paso)

18. Los pasos son:
• Colocar junto a la matriz dada la matriz unidad
• Conseguir hacer 0´s todos los elementos
debajo de la diagonal principal
• Hacer 1´s en la diagonal principal
• Hacer ceros todos los elementos por encima
de la diagonal principal

19. Transformaciones Básicas
• Las operaciones que se utilizan en este caso
son:
• Intercambiar filas
Fi   Fj
• Multiplicar una fila por un escalara
Fi = (c)Fi

20. Encontrar la matriz inversa de:
1 2 1
0 1 1
2 1 0
A =

21. Paso 1
• Crear una matriz aumentada con la matriz
original y una matriz identidad del mismo
orden
1 2 1 | 1 0 0
0 1 1 | 0 1 0
2 1 0 | 0 0 1

22. Paso 2
• Volver “0” los terminos de la primera columna
que no sean la primera fila
F3  F3 – (2)F1
1 2 1 | 1 0 0
0 1 1 | 0 1 0
0 -3 -2 | -2 0 1

23. Paso 3
• Convertir en 0´s los elementos de la segunda
columna, a excepción del de la segunda fila
F1  F1 – (2)F2
F3  F3 + (3)F2
1 0 -1 | 1 -2 0
0 1 1 | 0 1 0
0 0 1 | -2 3 1

24. Paso 4
• Convertir en 0’s los elementos de la tercera
columna, excepto el de la fila 3
F1  F1 + F3
F2  F2 – F3
1 0 0 | -1 1 1
0 1 0 | 2 -2 -1
0 0 1 | -2 3 1

25. Solución
• Para dar por concluido, la parte izquierda de la
matriz aumentada debe ser una matriz
identidad; y con esto podemos decir que la
parte derecha es la matriz inversa de “A”

26. A | (Id) =
Id = Identidad
= (Id) | A-1