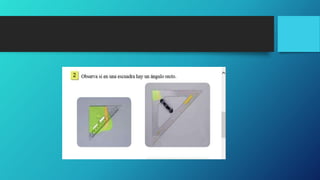
1. El documento presenta información sobre figuras geométricas como triángulos, cuadrados y ángulos. 2. Explica las características de diferentes tipos de triángulos y cuadriláteros y cómo medir y construir ángulos. 3. El objetivo es que los estudiantes reconozcan y comprendan las figuras geométricas a través de actividades prácticas.

1. CENTRO REGIONAL DE EDUCACIÓN NORMAL
DR. GONZALO AGUIRRE BELTRÁN
LIC. EN EDUCACIÓN PREESCOLAR
MATERIA: FORMA, ESPACIO Y MEDIDA
MTRA: DRA. HERCY BAÉZ CRUZ
INTEGRANTES:
GRUPO: “A” GRADO: 2° SEMESTRE
FECHA: 26 DE FEBRERO DEL 2015
• ESTAMBULI GUTIERREZ VIRGINIA GUADALUPE
• DILIEGROS CAMPILLO KAREN LIZBETH
• MÉNDEZ CHAMORRO ANDREA MAGDALENA
• TENORIO OLIVAREZ CARMEN JAQUELIN
• TRINIDAD AMBROCIO YANELY
• ZARATE MONTIEL JESSICA KRISTELL

2. FIGURAS GEOMÉTRICAS

3. ¿QUÉ SON LAS FIGURAS GEOMÉTRICAS?
Son las representaciones planas con determinados
números de lados y características definidas.
De igual manera una figura geométrica es
un conjunto no vacío cuyos elementos son puntos.

4. LADOS Y VÉRTICES
PUNTO (VÉRTICE) LINEA RECTA (LADOS)

5. Al unir los puntos con líneas rectas el alumno se
dará cuenta que se formara una figura (plano) .
Identificara cuantos puntos y líneas rectas tiene la
figura geométrica
Comprenderá que el número de puntos , son el
número de vértices y el numero de líneas rectas
son los lados que tienen las figuras. Es decir
identificará las propiedades o características.

6. ÁNGULO RECTO
• Un ángulo recto es aquel que mide 90°.Sus dos lados son
dos semirrectas perpendiculares, y el vértice es el origen de
dichas semirrectas.

7. Los ángulos rectos se encuentran en algunas figuras
geométricas planas, por ejemplo:
• Un triángulo rectángulo tiene un ángulo recto.
• Un cuadrado tiene cuatro ángulos rectos.

11. RECTÁNGULOS Y CUADRADOS
Cuadrilátero se define por
Cuatro-lados.
• Ángulos rectos
Un ángulo recto es un ángulo que mide
exactamente 90°
Hay 5 tipos distintos de cuadriláteros
• Cuadrado
• Rectángulo
• Rombo
• Romboide
• trapecio

12. Cuadrado Rectángulo Romboide Rombo
Trapecio

16. ESTOS SON LOS
CUADRILÁTEROS
QUE EL NIÑO DEBE
ENCONTRAR.

17. RELACIONANDO LAS
FIGURAS CON EL
ENTORNO.
CREACIÓN DE
OTRAS FIGURAS
MEDIANTE UNA.

18. TRIÁNGULO RECTÁNGULO
Un ángulo de 90 grados.
Triángulo rectángulo
isósceles
Triángulo rectángulo
escaleno

19. TRIÁNGULO
RECTÁNGULO

20. El triángulo es un polígono de tres lados.
TRIÁNGULOS

21. • Esta figura geométrica se logra a
partir de la unión de tres rectas
que se interceptan en tres puntos
desalineados. Cada uno de estos
puntos donde las rectas se unen
recibe el nombre de vértice,
mientras que los segmentos que
se pueden apreciar en la figura
reciben el nombre de lados.

22. TRIÁNGULO ESCALENO
El triángulo escaleno o también
denominado triángulo desigual,
se caracteriza porque todos sus
lados disponen de extensiones
diferentes. En ningún triángulo
de este tipo habrá dos ángulos
que dispongan de la medida.
Entonces en este ángulo no hay ni
ángulos ni lados idénticos.

23. CARACTERÍSTICAS
● Sus lados tienen longitudes diferentes.
● En un triángulo escaleno no hay dos ángulos que tengan la misma
medida.

24. TRIÁNGULO ISÓSCELES
• El triángulo isósceles es un polígono
de tres lados, siendo dos iguales y el
otro desigual.
• Por lo tanto, los ángulos también
serán dos iguales (α) y el otro
diferente (β), siendo éste el ángulo
que forman los dos lados iguales (a).
• La altura (h) del triángulo isósceles
se puede calcular a partir del
teorema de Pitágoras.

25. TRIÁNGULO EQUILÁTERO
• En geometría, un triángulo
equilátero, es un polígono regular
con tres lados iguales.
• En la geometría euclídea tradicional,
los triángulos equiláteros también
son equiangulares, es decir, los tres
ángulos internos también son
congruentes entre sí, cada ángulo
vale 60°.

27. 1.-Cada ángulo mide menos
de 90°
2.- Solo dos ángulos miden
los mismo en un triángulo
isósceles
3.- En un triángulo
equilátero sus tres lados
miden lo mismo.

28. Triángulo Equilátero:
Tres lados iguales
Tres ángulos iguales, todos 60°
Triángulo Escaleno:
No hay lados iguales
No hay ángulos iguales
Triángulo Isósceles:
Dos lados iguales
Dos ángulos iguales

29. COMO TRAZAR
TRIÁNGULOS
★ Localizar dos punto en el
espacio y trazar una recta
llamada BC (3 cm), con
ayuda de la regla
localizar el vértice A (4
cm).
★ Trazar una línea recta de
3 cm llamado segmento
BC, esta vez con ayuda de
tu compás abrir 4 cm y
encontrar el vértice A.

30. ACTIVIDADES
d) Isósceles
e)Equilátero
f) Escaleno

31. MEDIDA

32. MEDIDA
•La medida es el resultado de una medición.
•En este sentido, podemos medir por ejemplo, el tamaño
de un objeto o la distancia entre dos puntos.
•Se conoce como medida al resultado de medir una
cantidad desconocida.

33. MEDIR
•Se refiere a la acción de determinar el valor de una magnitud
•Lo que hacemos es comparar una cosa con otra, es decir, comparamos
una magnitud con respecto a otra.
•¡Eso es medir, comparar!
•Hemos medido nuestra estatura con otro compañero, la velocidad en
una carrera, el tiempo que nos lleva realizar un trabajo, la cantidad de
agua que cabe en una botella, la temperatura de nuestro cuerpo, etc.

34. MEDICIÓN DIRECTA
Medida directa es aquella que se realiza aplicando un aparato para
medir una magnitud, por ejemplo, medir una longitud.
Ejemplo:

35. MEDICIÓN INDIRECTA
La medida indirecta se da cuando se calcula el valor de la medida
mediante una fórmula.
Expresión matemática.
El cálculo de la fórmula se da por medio de las medidas directas.
†Área
†Perímetro
†Volumen

36. INSTRUMENTOS DE MEDICIÓN
 Regla y Metro
 Escuadras
 Transportador
 Balanza
 Bascula
 Espectrómetro
 Calendario
 Reloj
 Termómetro
 Barómetro

37. TIPOS DE ÁNGULOS

39. EL TRANSPORTADOR DE ÁNGULOS O
GINIÓMETRO
El transportador de ángulos es una herramienta de dibujo que nos
permite medir y construir ángulos. Consiste en un semicírculo
graduado de 180° con el que podemos medir ángulos convexos.
También hay transportadores que consisten en un círculo graduado
de 360°.

40. ¿CÓMO CONSTRUIR ÁNGULOS UTLIZANDO
TRANSPORTADOR?
• Trazamos una recta y señalamos sobre ella el vértice de ángulo que se
desea construir.
• El centro del transportador tiene que coincidir con el vértice del ángulo.
• Identificamos la medida del ángulo que vamos construir y marcamos los
grados que queremos, para posteriormente con ayuda de la regla unir esa
marca con el vértice del ángulo

41. EJEMPLO

42. ¿CÓMO MEDIR ÁNGULOS USANDO
TRANSPORTADOR?
1. El centro del transportador se coloca sobre el vértice
del ángulo que se va a medir.
2. Se hace coincidir uno de los lados del ángulo con la
línea horizontal del transportador y se lee en el
semicírculo o círculo graduado el valor marcado por el
otro lado del ángulo.

43. EJEMPLO

45. TAMAÑO DE LOS ÁNGULOS

49. CONCLUSIÓN
Logramos darnos cuenta respecto a las actividades anteriores
que las figuras geométricas se encuentran en nuestro
alrededor, ya sea en nuestras casas, lugares de trabajo, etc.
El niño puede llegar a la creación de figuras mediante el punto
y la línea recta, como las actividades mencionadas
anteriormente.
Y mediante estas, refuerza los conocimientos previos que tiene
a cerca de las figuras geométricas, ya que hace mención de
las características de las mismas, utilizando las herramientas
que encuentra a su alrededor, por ejemplo material concreto.