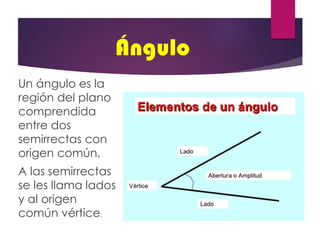
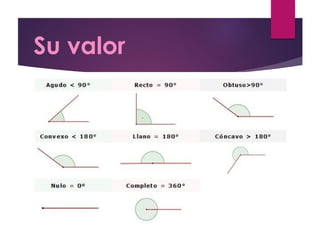
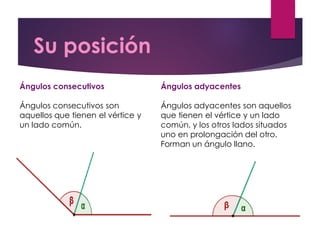
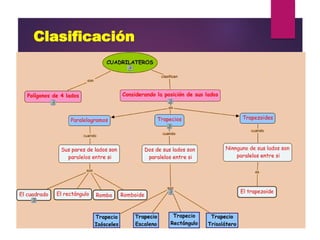
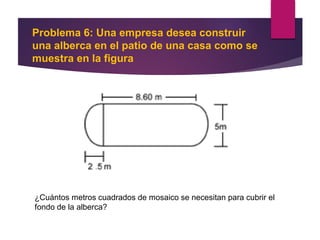
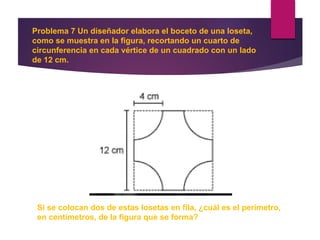
Este documento presenta información sobre geometría, incluyendo definiciones y propiedades de puntos, líneas, ángulos, polígonos, circunferencias y figuras geométricas. El propósito es que los estudiantes amplíen sus conocimientos sobre estos conceptos geométricos y sus aplicaciones en la vida cotidiana. Incluye ejercicios y actividades para practicar.