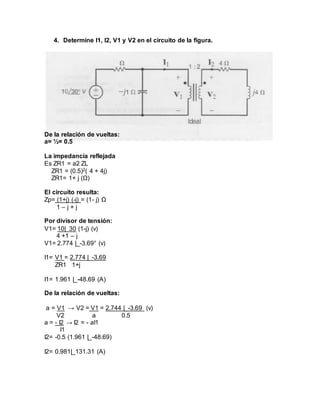
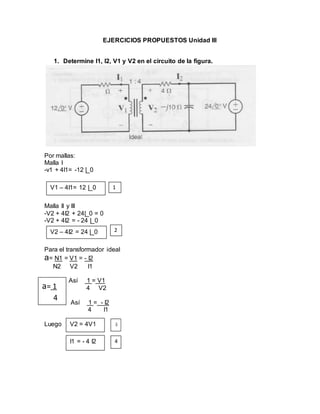
Este resumen describe los ejercicios propuestos en la unidad III de Circuitos Eléctricos II para la alumna María Daniela Álvarez. El primer ejercicio involucra determinar las corrientes e intensidades en un circuito dado utilizando las leyes de mallas. El segundo ejercicio pide hallar la corriente Io en un circuito dado utilizando las leyes de mallas y nodos. El tercer ejercicio solicita encontrar el voltaje Vo aplicando las leyes de mallas y Ohm. El cuarto ejercicio pide determinar las corrientes

1. UNIVERSIDAD “FERMIN TORO”
VICERRECTORADO ACADEMICO
FACULTAD DE INGENIERIA
CABUDARE EDO. LARA
CIRCUITOS ELECTRICOS II
Alumna:
María Daniela Álvarez
CI: 17784337
Cabudare, Julio 2015

2. EJERCICIOS PROPUESTOS Unidad III
1. Determine I1, I2, V1 y V2 en el circuito de la figura.
Por mallas:
Malla I
-v1 + 4I1= -12 |_0
Malla II y III
-V2 + 4I2 + 24|_0 = 0
-V2 + 4I2 = - 24 |_0
Para el transformador ideal
a= N1 = V1 = - I2
N2 V2 I1
Así 1 = V1
4 V2
Así 1 = - I2
4 I1
Luego
a= 1
4
V2 = 4V1
I1 = - 4 I2 4
V2 – 4I2 = 24 |_0 2
V1 – 4I1= 12 |_0 1

3. Sustituimos 3 en 2 y 4 en 1
V1 – 4(-4I2) = 12|_0
4 x 5 + 6 {16 V1 – 16 I2 = 96 |_0
V1 + 16 I2 = 12|_0
→ 17 V1 = 108|_0
V1 = 108 |_0
17
V1 = 6.353 |_0
Con lo cual
V2 = 4V1= 4(6.353|_0)
V2= 25.412 |_0 (v)
De 6:
I2 = 12|_0 – V1
16
= 12|_0 – 6.353 |_0
16
I2 = 0.353 |_0 (A)
De 4:
I1 = - 4 (0.353 |_0) A
I1= 1.412|_180° (A)
4V1 – 4I2 = 24|_0 5
V1 + 16 I2 = 12 |_0 6

4. 2. En el circuito mostrado, halle Io
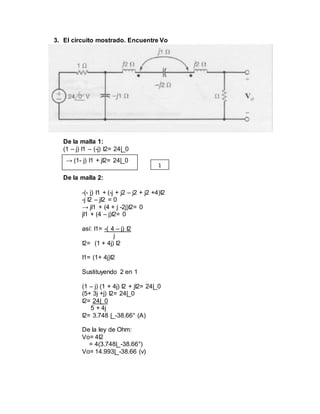
De la malla 1
(2 – j4 + j2 +4 ) I1 – 4I2 – jI2= 32|_0
De la malla 2
-4I1 + (4+ j2 – j2 +3) I2 – jI1= 0
→ - (4 + j)I1 + (7I2) = 0
→
Sustituyendo 2 en 1
(6 – j2) I1 – (4+j) (4+j / 7)I1= 32|_0
→ [(6 – j2) – 2.143 – 1.143j] I1= 32|_0
→ (3.857 – 3.143j)I1 = 32 |_0
→I1= 32|_0
3.857 – 3.143j
I1 = 6.432 |_39.18° (A)
De 2:
I2= (4+j / 7) 6.432 |_39.18
I2= 3.788 |_53.21 (A)
Finalmente Io = I2 = 3.788|_ 53.21°
→ (6 – j2) I1 – ( 4 + j) I2 = 32 |_0
1
I2 = (4+ j / 7) I1 2

5. 3. El circuito mostrado. Encuentre Vo
De la malla 1:
(1 – j) I1 – (-j) I2= 24|_0
De la malla 2:
-(- j) I1 + (-j + j2 – j2 + j2 +4)I2
-j I2 – jI2 = 0
→ jI1 + (4 + j -2j)I2= 0
jI1 + (4 – j)I2= 0
así: I1= -( 4 – j) I2
j
I2= (1 + 4j) I2
I1= (1+ 4j)I2
Sustituyendo 2 en 1
(1 – j) (1 + 4j) I2 + jI2= 24|_0
(5+ 3j +j) I2= 24|_0
I2= 24|_0
5 + 4j
I2= 3.748 |_-38.66° (A)
De la ley de Ohm:
Vo= 4I2
= 4(3.748|_-38.66°)
Vo= 14.993|_-38.66 (v)
→ (1- j) I1 + jI2= 24|_0
1

6. 4. Determine I1, I2, V1 y V2 en el circuito de la figura.
De la relación de vueltas:
a= ½= 0.5
La impedancia reflejada
Es ZR1 = a2 ZL
ZR1 = (0.5)2( 4 + 4j)
ZR1= 1+ j (Ω)
El circuito resulta:
Zp= (1+j) (-j) = (1- j) Ω
1 – j + j
Por divisor de tensión:
V1= 10|_30 (1-j) (v)
4 +1 – j
V1= 2.774 |_-3.69° (v)
I1= V1 = 2.774 |_-3.69
ZR1 1+j
I1= 1.961 |_-48.69 (A)
De la relación de vueltas:
a = V1 → V2 = V1 = 2.744 |_-3.69 (v)
V2 a 0.5
a = - I2 → I2 = - aI1
I1
I2= -0.5 (1.961 |_-48.69)
I2= 0.981|_131.31 (A)

7. NOTA:
a- El valor de la resistencia faltante es el 5to dígito de su número de cédula,
si es cero escoja el inmediato superior.
b- Cada ejercicio debe ser realizado paso por paso y explicado.