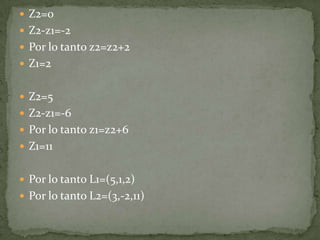
Este documento presenta dos problemas de cálculo vectorial. El primer problema involucra calcular el ángulo entre dos líneas rectas paramétricas. El segundo problema involucra calcular el ángulo entre dos vectores dados sus coordenadas. Ambos problemas se resuelven aplicando fórmulas de cálculo vectorial como el producto punto y la norma de un vector.

1. TECNOLOGICO DE ESTUDIOS
SUPERIOES DE JILOTEPEC
Alumnos: ALEJANDRO COLIN
ESTRADA Y EDGAR RAMIREZ
FLORES
MAESTRO: ING. RODOLFO
ALCANTARA ROSALES
MATERIA: CALCULO VECTORIAL
NOMBRE DE LA ACTIVIDAD:
PROBLEMAS

2.  EL PRESENTE TRABAJO CONTIENE DOS
PROBLEMAS, LOS CUALES SON SOBRE SACAR LOS
ANGULOS QUE FORMAN LAS LINEAS RECTAS
PARAMETRICAS, Y CON EL CUAL SE PRETENDE
PONERLO EN PRACTICA EN LA VIDA DSIARIA, YA
QUE EN LA CARRERA DE INGENIERIA CIVIL ES
MUY UTIL SABER SACAR ANGULOS.

3.  A) X1=4-t X2=5+2s
 Y1= 3+2t Y2=1+3s
 Z1=-2t Z2=5-6s
 X=x1+ta
 Y=x2+ta
 Y=(x2, y2, z2)+t(x2-x1,y2-y1,z2,z1)
 X=x2+t(x2-x1)
 Y=y2+t(y2-y1)
 Z= z2+t(z2-z1)

4.  X2=4 y2=3
 X2-x1=-1 y2-y1=2
 Por lo tanto x1=x2+1 por lo tanto y1=y2-2
 X1= 5 y1=1
 X=x2+5(x2-x1) y2=1
 X2=5 y2-y1=3
 X2-x1=2 por lo tanto y1=y2-3
 Por lo tanto x1= x2-2 y1=-2
 X1=3

5.  Z2=0
 Z2-z1=-2
 Por lo tanto z2=z2+2
 Z1=2
 Z2=5
 Z2-z1=-6
 Por lo tanto z1=z2+6
 Z1=11
 Por lo tanto L1=(5,1,2)
 Por lo tanto L2=(3,-2,11)

6.  PRODUCTO PUNTO
 L1-L2=(5*3)+(1x-2)+(2*1)
 =15-2+22
 =35
 Ѳ= arc cos 35 = 35 =0.553=56º25”30”
 (5.47)(11.57) 63.28
 L1= √x² + y² + z² L2= √x² + y² + z²
 L1= √25 + 1 + 4 L2= √9 + 4 + 121
 L1= √30 L2= √134
 L1= 5.47 L2= 11.57

7. 

 X-2 = y-5 = z-1
2 7 -1
x+3 = y-4 = z
-2 4
Formula
X= x ₂ +t(x ₂ -x ₁)
Y= y₂ + t(y 2 –y1)
Z= z2 +t(z2 -z1

8.  x2 - x1 = y2 - y1 = z2 - z1
 x2 - x1 y2 - y1 z2 - z1
 Despejando a t de la ecuación 1
 t= x2 - x1
 x2 - x1
 Para λ= x2= 1
 x2 - x1 = 2
 x= 1

9.  Despejando a t de la ecuación 2
 y2 - y1
 y2 - y1
 Para λ= y2=-5
 y2 – y1 =7
 y = -12
 Despejando a t de la ecuación 3
 z2 - z1
 z2 - z1
 Para λ=z2=1 λ1=(-2,-12,2)
 z2 – z1 = -1
 z =2

10.  PARA λ ₂
 X2 = 3
 X2 – X1=-2 X= -1
 Y2 = 9
 Y2– y1 = 1 y =8 λ₂ =(-2, 8, -4)
 Z2 = 0
 Z2 – z1 =4 z=-4

11.  r= r1+ t a vectorial
 X= x2 + t(x2 –x1)
 Y= y2 +t(y2 – y1 )
 Z= z2 + t(z2 – z1 )
 Producto punto
 λ1= (-2, -12, 2)
 λ2=(-1 , 8, -4 )
 Θ=arcos[λ1* λ2]
 ll λ1ll λ2 ll
 Θ=arccos-0.95
 Θ=161.98

12.  En estos ejercicios que realizamos de calculo
vectorial nos ayuda mucho en la realización para
nuestra carrera para sacar ángulos a partir de
coordenadas rectangulares o polares etc.