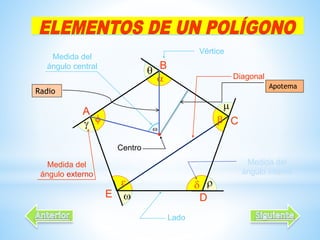
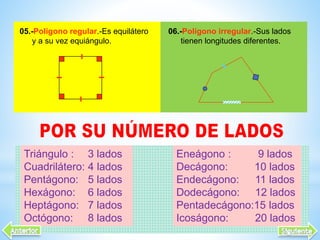
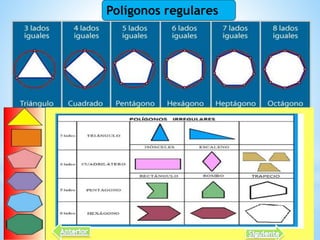
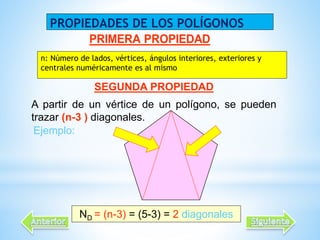
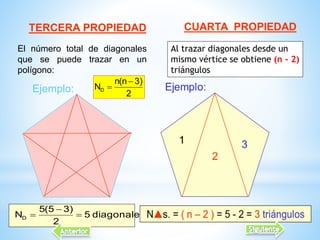
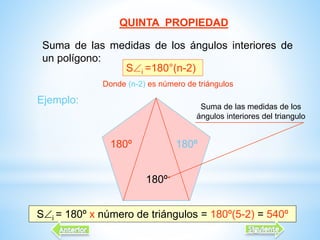
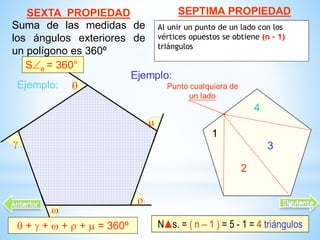
Este documento describe las propiedades de los polígonos. Define los diferentes tipos de polígonos como convexos, cóncavos, equiláteros y equiángulos. Explica que un polígono se forma uniendo segmentos de línea recta por sus extremos. Luego enumera las propiedades de los polígonos como el número de lados, diagonales, ángulos internos y externos. Finalmente, da ejemplos de fórmulas para calcular estas propiedades en polígonos regulares.

1. BENITO EUFEMIO HUAYNA AGUILAR
Grupo n° 01 Aula n° 101

3. Es la figura que esta formado por segmento de
recta unido por sus extremos dos a dos.

4. Medida del
ángulo central

A
B
C
DE








 Diagonal
Vértice
Medida del
ángulo
Lado
Medida del
ángulo interno
Centro
Apotema
Radio

5. 01.-Polígono convexo.-Las medidas
de sus ángulos interiores son
agudos.
02.-Polígono cóncavo.-La medida
de uno o mas de sus ángulos
interiores es cóncavo.
03.-Polígono equilátero.-Sus lados
son congruentes.
04.-Polígono equiángulo.-Las medidas
de sus ángulos interiores son
congruentes.

6. Triángulo : 3 lados
Cuadrilátero: 4 lados
Pentágono: 5 lados
Hexágono: 6 lados
Heptágono: 7 lados
Octógono: 8 lados
Eneágono : 9 lados
Decágono: 10 lados
Endecágono: 11 lados
Dodecágono: 12 lados
Pentadecágono:15 lados
Icoságono: 20 lados
05.-Polígono regular.-Es equilátero
y a su vez equiángulo.
06.-Polígono irregular.-Sus lados
tienen longitudes diferentes.

7. Polígonos regulares

8. SEGUNDA PROPIEDAD
A partir de un vértice de un polígono, se pueden
trazar (n-3 ) diagonales.
Ejemplo:
ND = (n-3) = (5-3) = 2 diagonales
PROPIEDADES DE LOS POLÍGONOS
n: Número de lados, vértices, ángulos interiores, exteriores y
centrales numéricamente es al mismo

9. TERCERA PROPIEDAD
El número total de diagonales
que se puede trazar en un
polígono:
2
)3n(n
ND

Ejemplo:
diagonales5
2
)35(5
ND 


Al trazar diagonales desde un
mismo vértice se obtiene (n - 2)
triángulos

10. QUINTA PROPIEDAD
Suma de las medidas de los ángulos interiores de
un polígono:
Si =180°(n-2)
Ejemplo:
180º
180º
180º
Si = 180º x número de triángulos = 180º(5-2) = 540º
Donde (n-2) es número de triángulos
Suma de las medidas de los
ángulos interiores del triangulo

11. SEXTA PROPIEDAD
Suma de las medidas de
los ángulos exteriores de
un polígono es 360º
Se = 360°





 +  +  +  +  = 360º
Ejemplo:
Al unir un punto de un lado con los
vértices opuestos se obtiene (n – 1)
triángulos

12. NOVENA PROPIEDAD
Número de diagonales
trazadas desde “V” vértices
consecutivos, se obtiene con
la siguiente fómula.
2
)2V)(1V(
nVND


Ejemplo:
2
1

13. 1ra. Propiedad 2da. Propiedad
3ra. Propiedad 4ta. Propiedad
Suma de las medidas de los
ángulos centrales.
Sc = 360°
Medida de un ángulo interior de
un polígono regular o polígono
equiángulo.
n
)2n(180
m
i


Medida de un ángulo exterior de
un polígono regular o polígono
equiángulo.
n
360
em


Medida de un ángulo central de
un polígono regular.
n
360
cm



14. Polígonos en la vida diaria