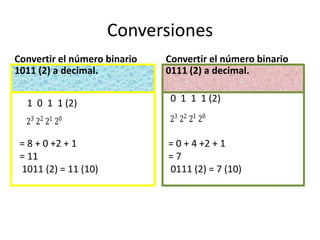
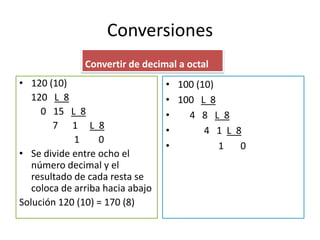
El documento explica los sistemas numéricos binario, octal y hexadecimal que utiliza la computadora para representar información como texto, datos, sonidos e imágenes mediante dígitos binarios. Describe que el sistema binario utiliza los símbolos 0 y 1, mientras que el hexadecimal utiliza 16 símbolos y el octal 8 símbolos. También cubre cómo convertir entre los sistemas decimal, binario, octal y hexadecimal.

2. Representación de la Información
• La computadora solo puede reconocer dos estados: apagado ó encendido,
los cuales se representan a través de los dígitos 0 y 1.
• Los cuatro tipos de información existentes textos, datos numéricos,
sonidos e imágenes son un conjunto de dígitos, es decir 0 y 1.

3. Sistemas Numéricos
• El estudio de las computadoras y del procesamiento de datos requiere
algún conocimiento de los sistemas numéricos, ya que éstos constituyen la
base de todas las transformaciones de información que ocurren en el
interior de la computadora.
• Entre estos sistemas tenemos los siguientes: sistema binario, sistema
octal, y sistema hexadecimal.

4. Sistema Binario
• El sistema binario, compuesto por los símbolos 1 y 0, es el que utiliza la
computadora en su funcionamiento interno. La computadora opera en
binario debido a que sus componentes físicos, pueden representar
solamente dos estados de condición: apagado/prendido, abierto/cerrado,
magnetizado/no magnetizado, etc. Estados de condición a los que se les
asigna el valor 1 ó 0.

5. Bit
• El bit es la unidad mínima de información empleada en informática, en
cualquier dispositivo digital, o en la teoría de la información. Es un dígito
del sistema de numeración binario.
• Un bit o dígito binario puede representar uno de esos dos valores, 0
(apagado) ó 1 (encendido).

6. Byte
• Unidad de información formada por ocho bits. Según cómo estén
combinados los bits (ceros o unos), formarán un byte y, por lo tanto,
un carácter cualquiera. Por ejemplo: la letra “a”, el número "2", incluso
un espacio.
• La forma en que se representan los bytes en la computadora se conoce
como código binario.
• a = 01100001

7. Conversión Decimal - Binario
• Para convertir números enteros de decimal a binario, la forma más simple
es dividir sucesivamente el número decimal y los cocientes que se van
obteniendo por 2, hasta que el cociente en una de las divisiones se haga 0.
• La unión de todos los restos obtenidos escritos en orden inverso nos
proporciona el número inicial expresado en el sistema binario.

8. Conversiones
Convertir el número decimal 10 a
binario
Convertir el numero decimal 26 a
binario
• 26 L 2
0 13 L 2
1 6 L 2
0 3 L 2
1 1 L 2
1 0
• 10 L 2
0 5 L 2
1 2 L 2
0 1 L 2
1 0
Solución 10 (10) = 1010 (2)

9. Sistema Decimal
• Utiliza como base el 10, que corresponde al número del
símbolo que comprende para la representación de
cantidades; estos símbolos son:
0 1 2 3 4 5 6 7 8 9

10. Binario a decimal
• El valor de cada posición es el de una potencia
de base 2, elevada a un exponente, los cuales
se colocan de derecha a izquierda. Una vez
realizado el cálculo de las potencias se suman
las cantidades.

11. Conversiones
0 1 1 1 (2)
23
22
21
20
1 0 1 1 (2)
= 8 + 0 +2 + 1
= 11
1011 (2) = 11 (10)
Convertir el número binario
1011 (2) a decimal.
Convertir el número binario
0111 (2) a decimal.
23
22
21
20
= 0 + 4 +2 + 1
= 7
0111 (2) = 7 (10)

12. Sistema Hexadecimal
• Es un sistema posicional de numeración en el que su base es 16, por tanto,
utilizara 16 símbolos para la representación de cantidades. Estos símbolos
son:
0 1 2 3 4 5 6 7 8 9 A B C D E F
SIMBOLOS VALOR ABSOLUTO
A 10
B 11
C 12
D 13
E 14
F 15

13. Binario a hexadecimal
• Análogamente, la conversión entre números hexadecimales y binarios se
realiza "expandiendo" o "contrayendo" cada dígito hexadecimal a cuatro
dígitos binarios.
• En caso de que los dígitos binarios no formen grupos completos (de tres o
cuatro dígitos, según corresponda), se deben añadir ceros a la izquierda
hasta completar el último grupo.

14. Conversiones
Convertir 101001110011
(2) a hexadecimal
• 101001110011 (2)
1010-0111-0011
A 7 3 (16)
Convertir 101001110011 (2) a
hexadecimal
• 111100000010 (2)
1111-0000-0010
F 0 2 (16)

15. Conversiones
Convertir de decimal a
hexadecimal
• 76 (10)
76 L 2
0 38 L 2
0 19 L 2
1 9 L 2
1 4 L 2
0 2 L 2
0 1 L 2
1 0
Primero convertimos el decimal a binario, luego
empezamos desde la derecha y tomamos 4
bits y los elevamos a la potencia, hacemos lo
mismo con los bits que restan.
1001100 (2)
100- 1100 = 4C
Solución 76 (10) = 4C (16)
Convertir de decimal a hexadecimal
• 50 (10)
50 L 2
0 25 L 2
1 12 L 2
0 6 L 2
0 3 L 2
1 1 L 2
1 0
110010 (2)
11 – 0010= 32
Solución 50 (10) = 32 (16)

16. Conversiones
Convertir de decimal a octal
• 120 (10)
120 L 8
0 15 L 8
7 1 L 8
1 0
• Se divide entre ocho el
número decimal y el
resultado de cada resta se
coloca de arriba hacia abajo
Solución 120 (10) = 170 (8)
• 100 (10)
• 100 L 8
• 4 8 L 8
• 4 1 L 8
• 1 0

17. Webgrafía
• https://es.wikipedia.org/wiki/Bit
• http://www.alegsa.com.ar/Dic/byte.php
• http://www.xtec.cat/~bfiguera/cucodigo.htm