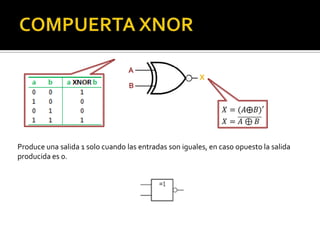
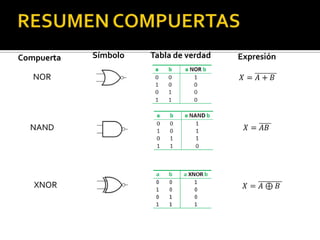
Este documento describe los conceptos fundamentales del álgebra booleana desarrollada por George Boole. En pocas oraciones: El álgebra booleana permite representar operaciones lógicas mediante símbolos algebraicos y tablas de verdad, lo que facilita el análisis y diseño de circuitos digitales basados en compuertas lógicas como AND, OR y NOT.

2. George Boole
¿Como es que se realizan decisiones lógicas con base en
circunstancias verdaderas o falsas (casos)?
Una investigación sobre las leyes del
pensamiento.
LOGICA

3. ALGEBRA
BOOLEANA
Símbolos
+
Operadores
A

4. Nivel lógico
Algebra
tradicional
Variables
Representan
números reales
Operadores Retornan números
Algebra
booleana
0 lógico
1 lógico
Falso
Verdadero
Representan solo 0
o 1.
Apagado
Encendido
Bajo
Alto
Retornan solo 0 o 1.
No
Si
Interruptor abierto
Interruptor cerrado
reales.
Operadores básicos
AND, OR, NOT
Ejemplo:
Don Ramón se pone bravo si doña Florinda le pega o el chavo le da bomba y la
chilindrina no lo consuela.
• F: Don Ramón se pone bravo. (F=1, don Ramón bravo; F=0 don Ramón
calmado).
• A: El chavo le da bomba a don Ramón.
• B: Doña florinda le pega a don Ramón.
• C: La chilindrina consuela a don Ramón.
F = (A OR
B)AND(NOT(C))
Expresión booleana

5. • Algebra booleana: Sistema algebraico que opera sobre variables booleanas. La
naturaleza binaria (de 2 estados) del algebra booleana la hace apta para el análisis,
simplificación y diseño de circuitos lógicos.
• Variables booleana: Variable que puede tomar
solo dos posibles valores, tales como
HIGH/LOW, 1/0, On/Off o TRUE/FALSE.
• Expresión booleana: Expresión algebraica
compuesta por variables booleanas y
operadores tales como AND, OR o NOT.
También es conocida como función booleana
o función lógica.
F = (A OR
B)AND(NOT(C))

6. OPERADORES
BOOLEANOS
LOGICOS BASICOS
AND
OR
Este operador retorna V solo
cuando ambas entradas son V.
Este operador retorna V
cuando cualquiera de las
entradas es V.
Ejemplo:
Dada la función lógica mostrada a continuación.
¿Cuál es su valor si A=1, B=0, D=0, C=0 y E=1?
NOT
Este operador retorna como
salida el valor opuesto a la
entrada.

7. Es una herramienta para describir la forma en que la salida de una función o
circuito lógico depende de los niveles lógicos presentes a la entrada.
Entradas (3) Salida
A
B
C
Circuito
lógico
x
Filas (8)
Para N entradas existen un total
de 2^N combinaciones posibles y
por ende 2^N filas en la tabla de
verdad asociada a la función que
esta se encuentra representando.
Ejemplo:
Se tiene un circuito con 3 entradas el cual se
enciende en los siguientes casos:
• Cuando dos de las entradas se encuentran en
alto.
• Cuando las tres entradas son iguales.
Llene la tabla de verdad asociada a este circuito.

8. Las funciones lógicas pueden representar circuitos lógicos.
Tabla de verdad
Función booleana
Circuito lógico
Compuerta lógica
Circuito electrónico que realiza una
función lógica booleana.

9. Compuerta AND
Inversor
A
A
B
Z
Compuerta NOR
A
B
Z
Compuerta NAND
Z
A
B
Compuerta OR
A
B
Z
Compuerta XOR
A
B
Z
Z

10. A
La operación NOT produce una salida cuyo valor
es el opuesto al valor de su entrada.
X

11. A
B
La operación AND produce una salida de
1 solo cuando todas sus entradas son 1.
En cualquier otro caso la salida es 0.
X

12. A
B
La operación OR produce una salida de 1
siempre que cualquiera de sus entradas
sea 0. En cualquier otro caso la salida es
0.
X

14. A
X
B
La operación NOR produce una salida de 1 solo cuando todas sus entradas son 0.
En cualquier otro caso la salida es 0.

15. A
X
B
La operación NAND produce una salida de 0 solo cuando todas sus entradas son 1. En
cualquier otro caso la salida es 1.

16. A
B
X
La operación XOR produce una salida de 1 cuando sus entradas son diferentes. En
cualquier otro caso la salida es 0.

17. A
X
B
Produce una salida 1 solo cuando las entradas son iguales, en caso opuesto la salida
producida es 0.

18. Compuerta
AND
OR
NOT
Símbolo
Tabla de verdad
Expresión

19. Compuerta
NOR
NAND
XNOR
Símbolo
Tabla de verdad
Expresión

20. Compuerta
XOR
Símbolo
Tabla de verdad
Expresión

21. Ejemplo 1: Determine la forma de onda de salida para la compuerta OR, cuando
se tiene la siguiente entrada a estas:

22. Ejemplo 2: Para la compuerta OR de 3 entradas mostrada a continuación,
determine la forma de onda a la salida.
Ejemplo 3: Como seria la salida si lo
que se tuviera fuera una compuerta
AND de 3 entradas

23. • ¿Cual es el único conjunto de condiciones de entrada que producirán
una salida baja en cualquier compuerta OR?
• ¿Escriba la expresión booleana para una compuerta OR de 6
entradas?
• ¿Si la entrada A del punto anterior permaneciera en alto, cual seria el
resultado de a la salida?
• ¿Cual es la única combinación de entradas que producirá un ALTO a la
salida de una compuerta AND de 5 entradas?
• ¿Cual es el nivel lógico que debería ser aplicado a la segunda entrada
de una compuerta AND de 2 entradas si la señal lógica en la primera
entrada es inhibida de buscar la salida?
• Cierto o falso: ¿ La salida de una compuerta AND siempre diferirá de
la salida de una compuerta OR para las mismas condiciones de
entrada?

24. • Cualquier circuito lógico, sin importar su complejidad, pueden ser
completamente descritos usando las tres operaciones básicas: OR, AND y
NOT.
¿Como se interpreta AB + C?
Se aplica un OR
entre A.B y el
termino C
Se aplica un AND
entre A y el termino
B+C
ORDEN DE PROCEDENCIA

25. • Las operaciones AND se hace antes que las operaciones OR
Los paréntesis hacen mas clara la
precedencia pero no son necesarios para el
caso anterior
• Cuando in inversor esta presente en un diagrama de circuito lógico, su expresión de
salida simplemente es igual a la expresión de entrada con una barra sobre esta.

26. La siguiente tabla muestra el orden de precedencia, siendo
la mas alta la que va de primero.

27. Evalué las siguientes expresiones booleanas, asumiendo que
a=1, b = 1, c = 0 y d = 1.
1. F = a*b + c
Respuesta: * tiene precedencia sobre +, así que cuando se
evalúa la expresión se tiene que F=(1*1) + 0 = 1 + 0 = 1.
2. F = ab + c
Respuesta: El problema es similar al anterior +, solo que en
este caso se usa la notación alternativa para la operación AND.
3. F = ab’
Respuesta: Primero debe evaluarse b’ por que el NOT tiene
precedencia sobre el AND, esto resulta en: F=1*(1’)=1*(0)=1*0=0.
4. F = (ac)’
Respuesta: Primero se evalúa lo que esta dentro de paréntesis para
luego se negar el resultado: F=(1*0)’=(0)’=0’=1.

28. Evalué las siguientes expresiones booleanas, asumiendo que
A=0, B = 1, C = 1 y D = 1.

29. Siempre que se tenga un circuito lógico combinacional y
desee saber como funciona, la mejor manera de analizarlo
es mediante el uso de una tabla se verdad.
Salid
a
Entrada
s
Nodos intermedios: No son
entradas ni salidas son solo
conexiones entre la salida de
una compuerta y la entrada
de otra

30. Ejercicio:
Muestre la tabla de verdad asociada a la siguiente función
lógica:

31. Cuando la operación de un circuito esta definida por una
función booleana, nosotros podemos dibujar el circuito
directamente de la expresión.

32. Dibuje el circuito que implementa la siguiente función
lógica:
Dibuje nuevamente el circuito pero esta vez asuma como
restricción que este no puede tener compuertas de mas de 3
entradas.

33. Dibuje el circuito que implementa la siguiente función
lógica:
Como restricción use compuertas que no tengan mas de dos
entradas.
Ahora siguiendo la misma restricción implemente en un
circuito digital la siguiente función lógica.

35. Postulados de Huntington
Las operaciones en algebra booleana están basadas en los siguientes
postulados:
x+y=y+x ;
xy = yx
En aplicación en los circuitos digitales podríamos decir que no importa el
orden de conexión de las entradas a una compuerta OR o AND.

36. x + (y+z) = (x + y)+z ;
x.(y.z) = (x.y).z
x + (y.z) = (x + y).(x+z) ; x.(y+z) = x.y + x.z

37. Postulado 5 (Identidades): En el conjunto S existen dos elementos 1
(uno) y 0 (cero), únicos, tales que:
x + 0 = x ; x.1 = x
x
0
x
x
1
x

38. Principio de dualidad:
Cualquier expresión algebraica derivada de los axiomas continua siendo
valida cuando los operandos AND y OR, y los elementos 1 y 0 son
intercambiados.

39. Teoremas
Teorema 1: Los elementos de identidad 0 y 1 son unicos.
Teorema 2 (Idempotencia):
(i) x + x = x
(ii) x.x = x
Teorema 3 (Elemento nulo):
(i) x + 1 = 1
(ii) x.0 = 0
Teorema 4 (Leyes de absorción):
(i) x + xy = x
(ii) x(x+y) = x
Teorema 5: Cada elemento en el conjunto S tiene un único complemento.

40. El cual generalizado para mas elementos mas de dos elementos será:

42. P5. Identidades: x.1 = x
P4. Propiedad distributiva: x(y+z) = xy + xz
T3. x + 1 = 1
P5. x.1 = x
P4. Propiedad distributiva: x+y.z = (x+y)(x+z)
P5. Identidades: x+1 = x
P4. Propiedad distributiva: x+y.z = (x+y)(x+z)

43. Una las principales aplicaciones es la simplificación de funciones lógicas, lo
cual tiene un efecto en la disminución del numero de compuertas que tendrá
al circuito lógico asociado a la función en cuestión. A este proceso se le
conoce como manipulación algebraica.
Ejemplo 1:
Simplifique la siguiente expresión utilizando las leyes y reglas de boole.
ab + a(b+c) + b (b+c) = ab + ab + ac + b + bc
= ab + ac + b (1+ c)
= ab + ac + b  1
= ab + ac + b
= b (a +1) + ac
= b  1 + ac
= b +ac

44. Ejemplo 2:
Simplifique la siguiente expresión utilizando las leyes y reglas de Boole.
Solución:
Forma 1
[ab.(c+bd) +ab]c = [b.(a.(c+bd)+a)].c
=b.a.c
Forma 2
[abc + abbd + ab]c = [abc + a(bb)d + ab]c
= [abc + a(1)d + ab]c
= (abc + ad + ab)bc
= (ab+ad)bc
= abbc + adbc
= abc + abcd
= abc

46. Ejemplo:
Use una tabla de verdad para definir una función F(a,b,c) que sea 1 cuando el numero
binario abc sea mayor o igual a 5.

47. • Podemos convertir desde una representación cualquiera a otra.
Circuito
Evaluar la ecuación para cada
combinación de entrada (fila).
Crear columnas
intermedias
ayuda
Tabla de
verdad
Ecuación
Hacer un OR de cada
termino de entrada cuya
salida sea 1

48. Una función puede ser representada en diferentes formas