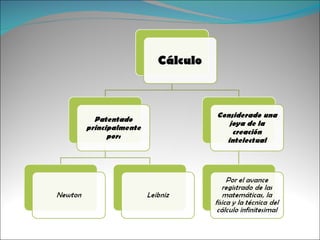
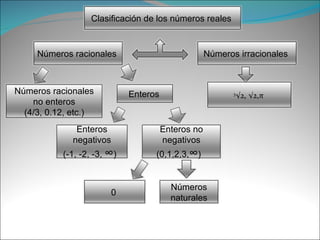
El documento presenta los temas a tratar sobre el cálculo diferencial e integral. Brevemente resume la historia del cálculo desde los siglos XVII al XX, destacando figuras como Euler, Cauchy y Dedekind. Explica la clasificación de los números reales y la notación de desigualdades. Finalmente, incluye ejercicios resueltos de desigualdades cuadráticas y lineales.

1. Temas a presentar:
Antecedentes del cálculo
Los números reales
Notación de Desigualdades
Ejercicios y Soluciones de Desigualdades

4. El siglo XVII y las
disputas por la
creación del cálculo
Se desarrollaron 4
problemas Dada una
Encontrar
científicos y fórmula de la
la tangente
matemáticos distancia
a una curva
en punto recorrida por un
cuerpo en
cualquier
Encontrar el tiempo conocido
valor máximo Encontrar la
ó mínimo de longitud de una
una cantidad curva, el área de
una región y el
volumen de un
sólido

5. El siglo XVIII y siglo XIX
El gran matemático de En este siglo un problema fue
este siglo fue el suizo definir el significado de la
Euler palabra función
Algunos personajes
Aportando ideas sobre propusieron pero en 1821
el cálculo y ramas de Cauchy consiguió un enfoque
las matemáticas y sus lógico del cálculo y esto llevo
aplicaciones aun problema nuevo el de la
definición de la lógica real.
Esto sirvió para acentuar Aunque la definición de
la falta de un desarrollo Cauchy estaba basado en
adecuado y justificado de este concepto el alemán
las ideas básicas del Dedekind quien encontró la
cálculo definición adecuada

6. El siglo XX y nuestros días
Durante la conferencia internacional de Matemáticas el
alemán David Hilbert retomo 23 problemas matemáticos ,
estos problemas fueron un estimulo de trabajos
matemáticos.
Se creo un avance digital que dio a impulsar a ciertas ramas
de la matemática. El ordenador permitió solucionar varios
problemas matemáticos que no se habían podido resolver
anterior mente .
Aunque la mayoría de los problemas mas importantes han
sido resueltos, otros siguen sin solución. Al mismo tiempo
aparecen nuevos problemas.

8. Clasificación de los números reales
Números racionales Números irracionales
Números racionales Enteros 3
√2, √2,π
no enteros
(4/3, 0.12, etc.)
Enteros Enteros no
negativos negativos
(-1, -2, -3, ∞) (0,1,2,3,∞)
Números
0
naturales

9. Notación de desigualdades
•Supongamos que A y B son dos números reales y a < b. Se usara la
notación a < x < b para decir que x es un número entre a y b, la expresión
a < x < b es equivalente a dos desigualdades.
•Intervalos
Se han a y b dos números reales con a < b, un intervalo cerrado,
denotado por [a , b], consiste en todos los números reales x para los
cuales a ≤ x≤ b, un intervalo abierto, denotado por (a , b), consiste en
todos los números reales x para lo que a < x < b.
•Intervalos semiabierto o semicerrado
(a , b] que consiste en todos los números reales x para lo que a < x ≤ b
[a , b) que consiste en todos los números reales x para los que a ≤ x < b.
Ejemplo:
X=[3,7) x= {3, 4, 5, 6, 6.99……} Se incluye el 3 pero el 7 no

10. •Ecuaciones y desigualdades que incluyen valor absoluto
Si a es un número real positivo y si u es cualquier expresión algebraica,
entonces:
|u| = a es equivalente a: u = a o u = -a
•Desigualdades que incluyen valor absoluto
Si a es un número real positivo y u una expresión algebraica, entonces:
|u| < a es equivalente a: –a < u < a (1)
|u| ≤ a es equivalente a: –a ≤ u ≤ a (2)
|u| > a es equivalente a: u > a ó u < -a (3)
|u| ≥ a es equivalente a: u ≥ a ó u ≤ -a (4)

11. i ón de
Sol uc
s y ades
ic i o ald
E jerc sigu
de

12. Se despeja
la x
para resol
A) 7 − 2 Χ ≥ −3 desiguald
ver la
ad
− 2 Χ ≥ −3 − 7 Cuando u
n numero Por ultimo se
negativo
− 2 Χ ≥ −10 multiplic
se pasa
ando o
grafica el
intervalo en
dividiend
−10 invierte e
o se la recta.
Χ≤ de la des
l símbolo
−2 igualdad.
Χ≤5
0
Intervalo : 1 2 3 4 5
[ − ∞,5]

13. Aquí se usa la forma de la
proposición(1): donde la
expresión u= 4x+2 que se
encuentra dentro de las
B) 4 Χ + 2 < 10 barras de valor absoluto.
El 2 pasa restando a
los dos lados de la
− 10 < 4 Χ + 2 < 10 desigualdad, al igual
que el 4 pasa
− 10 − 2 < 4 Χ < 10 − 2 dividiendo.
Se grafica el
intervalo
− 12 < 4 Χ < 8
− 12 8
<Χ<
4 4 (
-4 -3 -2 -1 1
)
2 3
0
−3< Χ < 2
Intervalo :
( − 3,2)

14. C) 0 ≤ 4 Χ − 1 ≤ −2 Al despejar x se
suma 1 en cada
lado y se dividen
entre 4 para poder
despejar la x.
0 + 1 ≤ 4Χ ≤ −2 + 1
Se grafica el
1 ≤ 4 Χ ≤ −1 intervalo.
1 −1
≤Χ≤
4 4
-1 0 1
Intervalo : -0.25 0.25
[ − 0.25,0.25]

15. Las desigualdades
cuadráticas se
D) Χ − 10 Χ − 200 ≤ 0
2
resuelven como
( Χ + 10)( Χ − 20) ≤ 0
ecuaciones
cuadráticas, en este
caso por el método de
Χ + 10 = 0 Χ − 20 = 0 factorización
Y ahora
Χ = − 10 Χ = 20 graficamos
Se le da un valor
-30 -20 -10 arbitrario a la x entre
0 10 20 30
los valores
Si X es igual a: 19 encontrados para
Sustituyendo: comprobar la
desigualdad.
La proposición es
( 0)2
−10( 0 ) −200 ≤ 0
verdadera, quiere
decir que los
0 −0 −200 ≤ 0 corchetes van
encontrados.
−200 ≤ 0 ; X=[-10 , 20]

16. Elaborado por:
Castillo García Marco Antonio
García Carrillo Paola
García Reyes Adrian Alfonso
Serna González Alicia
Serna González Rosamelia
Maestro Asesor: Luis Enrique Valadez Morales