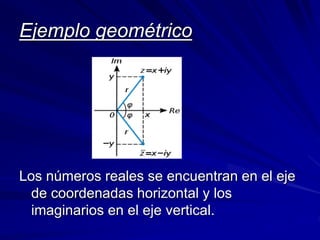
Este documento describe la historia y uso de los números complejos. Los números complejos se desarrollaron durante el Renacimiento para resolver raíces cuadradas de números negativos. Se representan con el símbolo i, donde i^2 = -1. Los números complejos se pueden sumar, multiplicar y usar para calcular impedancias eléctricas y resolver ecuaciones diferenciales.

1. Números complejos
Análisis Matemático
Profesor: Miguel Díaz

2. Historia
Los números complejos se crearon en Italia,
durante el periodo del renacimiento,
cuando por vez primera los algebristas se
dedican a investigar seriamente estos
números y penetran el lado misterioso en
que se hallaban envueltos desde la
antigüedad, los matemáticos se
encontraron con el problema de resolver
la raíz cuadrada de un numero negativo.

3. Explicación:
Como no todos los problemas pueden resolverse
con números reales, se aprendió que era
posible calcular la raíz cúbica de -1 o de -8.
Sabemos por ejemplo, que la raíz cúbica de -1
es igual a -1.
Simplemente porque (ahora al revés) (-1)^3 = -1.

4. Pero cuando se quiere obtener la raíz de -4
por ejemplo
si probamos con 2 no puede ser
porque 2^2 = 4, y si probamos con -2,
tampoco es porque(-2)^2=4, también da 4.
Por este inconveniente se inventaron los
números complejos

5. El símbolo que se utiliza para simbolizarlos es la
letra (i), de imaginarios, porque son números que
no se pueden representar en la coordenadas reales
como hacemos habitualmente.
i^2=-1
Entonces para el ejemplo anterior, en donde se
desea obtener, la raíz cuadrada de -4, la
respuesta es: i2 de tal manera que si hacemos al
revés, es decir, 2i . 2i = 4. i^2 = 4. (-1)= -4

6. Por otro lado, si vamos a tener un
producto asociativo, conmutativo y
distributivo
respecto de la suma, se deberá tener
(a + bi)(c + di) = ac + bdi^2 + adi + bci = ac
- bd + (ad + bc)i.
Con esto ya sabríamos sumar y
multiplicar complejos.

7. Operación de números complejos
Suma y diferencia: Se realiza sumando y
restando partes reales entre sí y partes
imaginarias entre sí
(5+2 i) + (-8+3 i)-(4-2 i)=
=(5-8-4) + (2+3+2) i = -7+7i
Multiplicación: el producto de los números
complejos se realiza aplicando la propiedad
distributiva del producto respecto de la suma y
teniendo en cuenta que i ^2 = −1
(5+2 i) . (2-3 i)=
=10-15 i +4 i-6 i ^2=10-11 i +6= 16-11 i

8. Ejemplo geométrico
Los números reales se encuentran en el eje
de coordenadas horizontal y los
imaginarios en el eje vertical.

9. Aplicación de los números
complejos en la electricidad
Una aplicación de los números complejos es el cálculo
de impedancias equivalentes en redes eléctricas a
corriente alterna. La “impedancia” eléctrica es la
oposición al flujo de la corriente eléctrica de cualquier
circuito. Por lo general, en los textos, la magnitud de la
impedancia Z se denota como /Z/

10. La principal utilización para los
números complejos es en los
cálculos eléctricos de circuitos.
También tienen muchas aplicación
en las ramas de la ingeniería.

11. Otros usos de los números
complejos
Los números complejos son usados en:
• Operaciones vectoriales
• Representación de magnitud
• Facilitan el manejo de funciones de ondas
• Para simplificar cuentas
• Resolución de ecuaciones diferenciales
• Para el procesamiento digital de señales

12. Alumnos:
Martín Perez, Nahuel Muñoz y
Mauricio Novasad