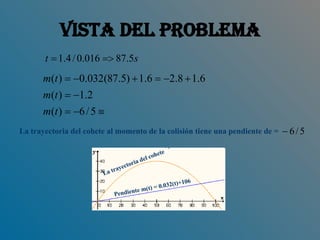
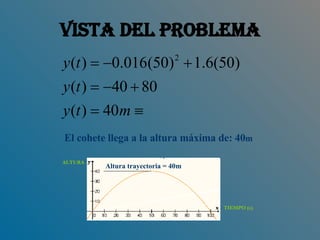
Este documento resume la resolución de un ejercicio de cálculo diferencial que involucra el movimiento de un cohete disparado desde la base de una colina. Se calcula la pendiente de la trayectoria del cohete en el momento del disparo, cuando choca contra la colina, y su altura máxima sobre el suelo utilizando conceptos como la regla del cociente, la suma y la diferencia, y las potencias.

1. APLICACION DE CALCULO DIFERENCIAL EN EL SIGUEINTE EJERCICIO:

2. EJERCICIO Un cohete que se tiene emplazado al pie de una colina cuya pendiente es 1/5 (y=x/5) se dispara hacia la loma y sigue una trayectoria dad por : Resolver: a. Cual es la pendiente de la trayectoria del cohete en el momento del disparo? b. Cual es la pendiente de la trayectoria cuando choca contra la colina? c. Calcule la altura máxima del cohete sobre el suelo?

3. Análisis del ejercicio Datos: Teorema 2.8: La Regla del Cociente:

4. SOLUCION DEL EJERCICIO a.) Pendiente de la trayectoria del cohete en el momento del disparo Teorema 2.8: La regla de la suma y la diferencia: Teorema 2.3: La regla de las Potencias:

5. VISTA DEL PROBLEMA La pendiente de la trayectoria del cohete al momento del disparo es = Pendiente m(x)= -0.032x+1.6 =8/5 Trayectoria del cohete Punto de origen (x)=0

6. SOLUCION DEL EJERCICIO b.) Pendiente de la trayectoria del cohete en el momento de la colisión Se Aplica Algebra común: Debemos conocer el tiempo (t) al momento del impacto por lo que se iguala las ecuaciones

7. VISTA DEL PROBLEMA La trayectoria del cohete al momento de la colisión tiene una pendiente de = La trayectoria del cohete Pendiente m(t) = 0.032(t)+106

8. SOLUCION DEL EJERCICIO c.) Altura máxima del cohete sobre el suelo Al alcanzar el cohete la altura máxima la recta tangente es = 0 Teorema 2.3 La regla de las Potencias Debemos conocer el tiempo (t) cuando el cohete llega a su altura máxima

9. VISTA DEL PROBLEMA El cohete llega a la altura máxima de: 40 m Altura trayectoria = 40m ALTURA TIEMPO (s)

10. Teoremas empleados

11. Teorema 2.8 : La Regla del cociente

12. Teorema 2.5 : La Regla de la suma y la diferencia Teorema 2.3 : La Regla de las potencias

13. Pendiente de una gráfica: m => m’(x)=0 Recta Tangente con pendiente m: y – y 1 = m (x –x 1 ) Aplicaciones Usadas

14. GRACIAS...!!!