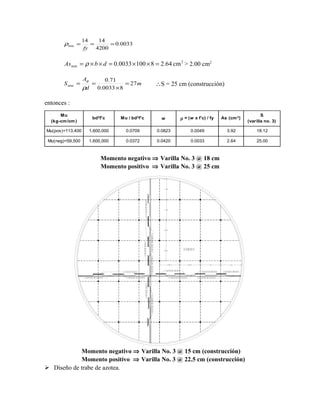
Este documento presenta los cálculos estructurales para un tanque circular de concreto armado con un diámetro de 44.2 metros y una altura de 3 metros. Se calculan las dimensiones, presiones del agua, espesor del muro, área de acero y diseño de la losa y trabes de la azotea. El tanque tiene una capacidad de 4,600 m3 y resistirá una carga máxima de 55,250 kg.

1. MEMORIA DE CALCULO ESTRUCTURAL DEL PROYECTO DE TANQUE
CIRCULAR DE CONCRETO ARMADO, PARA ALMACENAR 4,600 m3
.
CONSTANTES DE DISEÑO
Concreto f’c = 250 kg/cm2
Acero de refuerzo fy = 4,200 kg/cm2
Peso volumétrico del concreto γ = 2,400 kg/m3
Peso volumétrico del agua γ = 1,000 kg/m3
Capacidad mínima de carga del suelo γ = 1,800 kg/m3
Cargas vivas 250 kg/m2
 Calculo de las dimensiones del tanque.
Altura propuesta (H) = 3.00 m
2
33.1533
3
4600
m
H
Vol
Area fondo ===
m44.2018.44
33.153344
⇒=
×
=
×
= m
Area
D
fondo
ππ
DIMENSIONES DEL TANQUE
Volumen de diseño 4,600 m3
Diámetro interior (D) 44.20 m
Nivel máximo de agua 3.00 m
Altura máxima de los muros hasta la losa 3.40 m
Bordo libre 0.40 m
 Cálculo de las presiones del agua a diferentes profundidades.

2. 2
h
P
γ
=
Para h1 = 3.00 m, h2 = 2.00 m y h3 = 1.00 m :
2
21
1
hh
P
γγ +
= ⇒
( ) 2
1 /500,2
2
)21000(31000
cmkgP =
×+×
=
2
2
2
h
P
γ
= ⇒
2
2 /500,1
2
31000
cmkgP =
×
=
2
3
3
h
P
γ
= ⇒
2
3 /500
2
11000
cmkgP =
×
=
2
PD
T =
2
1
1
DP
T = ⇒ kgT 250,55
2
20.44500,2
1 =
×
=
2
2
2
DP
T = ⇒ kgT 150,33
2
20.44500,1
2 =
×
=
2
3
3
DP
T = ⇒ kgT 050,11
2
20.44500
3 =
×
=
Por lo tanto
TMAX = 55,250 kg

3.        
         



4.  Calculo del espesor mínimo del muro circular.
max
100
T
fctfs
nfctfscEs
h
×
−+
=
c = 0.0003
fs = 1,500 kg/cm2
fct = 26 kg/cm2
TMAX = 55,250 kg
Es = 2.10 x 106
kg/cm2
n = 9
m
x
h 86.26250,55
26500,1100
)269(500,1)1010.20003.0( 6
=×





××
×−+×
=
∴ Espesor = 27 cm
 Calculo del area de acero del muro considerando articulación plástica en la unión del
muro con el fondo, lo cual nos da una mayor seguridad.
Para T1 = 55,250 kg
colocados en dos capas será φ ¾” @ 14 cm por parrilla.
Para T2 = 33,150 kg
colocados en dos capas será φ ¾ ” @ 18 cm por parrilla.
Para T2 = 11,050 kg
fs
T
As =
2
1 83.36
500,1
250,55
cmAs ==
2
2 10.22
500,1
150,33
cmAs ==

5. colocados en dos capas será φ 5/8” @ 18 cm por parrilla.
Nota. El colocar un poco más de acero aumenta su vida útil para la corrosión.
D E T A L L E D E L A R M A D O D E L M U R O
 Diseño estructural de la losa de azotea del tanque.
2
3 37.7
500,1
050,11
cmAs ==

6. Análisis de cargas.
Peso propio de losa (12 cm) =288 kg/m2
Impermeabilizantes y enjarres = 32 kg/m2
wm = 320 kg/m2
Cargas vivas wv = 250 kg/m2
1==
lb
la
m
Donde:
la = lado corto
lb = lado largo
50.0
1
1
41 =
+
=
m
k
50.0
1 4
4
2 =
+
=
m
m
k
Por lo tanto:
wm = 0.50 x 320 =160 kg/m
wv = 0.50 x 250 =125 kg/m
6 claros @ 5.50 m = 33.00 m
2 claros @ 5.60 m = 11.20 m
= 44.20 m
Para el cálculo estructural se procedió a utilizar el programa “General Frame
Análisis v2.05”, del cual nos proporciona las fuerzas axiales, cortantes y momentos
máximos y mínimos para las condiciones de cargas ilustradas en la figura. Tomando en
cuenta la siguiente consideración:
La resistencia requerida WT que debe resistir la carga muerta (wm) y la carga viva
(wv) deberá ser por lo menos igual a (Reglamento ACI 318 “9.2.1.”) :
WT = 1.4 wm + 1.7wv
Datos
5.60 m 5.50 m 5.50 m 5.50 m 5.50 m 5.50 m 5.50 m 5.60 m 3.40 m
w1
= k1
wu
w2
= k2
wu
5.50 m
5.50 m

7. f’c = 250 kg/cm2
E = 210,000 kg/cm2
f’y = 4,200 kg/cm2
Muros A = 2,700 cm2
d = 8 cm I = 164,000 cm4
h = 12 cm Losa 12 cm A = 1,200 cm2
b = 100 cm I = 14,400 cm4
Nodo ⇒
Elemento ⇒
Resultados.
Momento negativo.
m/m-kg134,1=negMu
Momento positivo.
m/m-kg595=posMu
Por lo tanto,
cfbd
Mu
w
'
88.1
718.0847.0 2
−−=
dbAs ××=ρ
d
A
S
ρ
φ
=
como:
Mu
(kg-cm/cm)
bd2
f'c Mu / bd2
f'c w ρ = (w x f'c) / fy As (cm2
)
S
(varilla no. 3)
Mu(pos)=113,400 1,600,000 0.0709 0.0823 0.0049 3.92 18.12
Mu(neg)=59,500 1,600,000 0.0372 0.0420 0.0025 2.00 35.53
1 2
3 4 5 6 7 8 9 10 11
3
1
4 5 6 7 8 9 10
2
1
1

8. 0033.0
4200
1414
min ===
fy
ρ
2
min cm64.281000033.0 =××=××= dbAs ρ > 2.00 cm2
m
d
A
S 27
80033.0
71.0
min =
×
==
ρ
φ
∴S = 25 cm (construcción)
entonces :
Momento negativo ⇒ Varilla No. 3 @ 18 cm
Momento positivo ⇒ Varilla No. 3 @ 25 cm
Momento negativo ⇒ Varilla No. 3 @ 15 cm (construcción)
Momento positivo ⇒ Varilla No. 3 @ 22.5 cm (construcción)
 Diseño de trabe de azotea.
Mu
(kg-cm/cm)
bd2
f'c Mu / bd2
f'c w ρ = (w x f'c) / fy As (cm2
)
S
(varilla no. 3)
Mu(pos)=113,400 1,600,000 0.0709 0.0823 0.0049 3.92 18.12
Mu(neg)=59,500 1,600,000 0.0372 0.0420 0.0033 2.64 25.00
    
  
  
            
                 
      



   
        
      
        

9. wm = 1,250 kg/m
wv = 550 kg/m
Para el cálculo estructural se procedió a utilizar el programa “General Frame
Análisis v2.05”, del cual nos proporciona las fuerzas axiales, cortantes y momentos
máximos y mínimos para las condiciones de cargas ilustradas en la figura.
Datos
b = 25 cm Trabes A = 1,175 cm2
h = 47 cm I = 216,297 cm4
d = 42 cm Columnas A = 900 cm2
f’c = 250 kg/cm2
I = 67,500 cm4
fy = 4,200 kg/cm2
Muros A = 2,700 cm2
E = 210,000 kg/cm2
I = 164,025 cm4
Nodo ⇒
Elemento ⇒
Resultados.
Momento negativo.
m/m-kg837,7=negMu
Momento positivo.
1
1
5.60 m 5.50 m 5.50 m 5.50 m 5.50 m 5.50 m 5.50 m 5.60 m 3.40 m
4800 Kg
1 9
10 11 12 13 14 15 16 17
2 3 4 5 6 7 8
10 11 12 13 14 15 16 17 18
2 3 4 8 97651

10. m/m-kg641,4=posMu
como:
0033.0
4200
1414
min ===
fy
ρ
2
min cm47.342250033.0 =××=××= dbAs ρ > 2.98 cm2
entonces :
⇒ Doblemente reforzada con 2 varillas No. 5 y 1 varilla No. 4
Cortante máximo actuante.
Vu = 8,186 Kg
Por lo tanto,
φ = 0.85
kg799,8422525053.0'53.0 =××== bdcfVc
kg832
85.0
)879985.0(8186
=
×−
=
−
=
φ
φVcVu
Vs
Según el Reglamento ACI 318 “11.5.4.” se tiene que si:
Mu
(kg-cm/cm)
bd2
f'c Mu / bd2
f'c w ρ = (w x f'c) / fy As (cm2
)
No. de barras
(varilla no. 4 y 5)
Mu(pos)=783,700 11,025,000 0.0711 0.0826 0.0049 5.16 1 y 2
Mu(neg)=464,100 11,025,000 0.0421 0.0477 0.0028 2.98 -----
Mu
(kg-cm/cm)
bd2
f'c Mu / bd2
f'c w ρ = (w x f'c) / fy As (cm2
)
No. de barras
(varilla no. 4 y 5)
Mu(pos)=783,700 11,025,000 0.0711 0.0826 0.0049 5.16 1 y 2
Mu(neg)=464,100 11,025,000 0.0421 0.0477 0.0033 3.47 1 y 2

11. 2
d
S =
4
d
S =
bdcfVs '1.1< ⇒ S = 60 cm bdcfVs '1.1> ⇒ S = 30 cm
b
Avfy
S
5.3
=
b
Avfy
S
5.3
=
como:
kg262,1842252501.1'1.1 =××=bdcf
entonces :
cm21
2
42
S ==
262,18832 < ⇒ S = 60 cm ∴S = 25 cm (construcción)
cm72.30
255.3
4200)32.0(2
=
×
×
=S
⇒ Estribos para amarre No. 2 @ 25 cm.
D E T A L L E D E L A R M A D O D E L A S T R A B E S
 Diseño estructural de la columna y zapata (ver calculo)
   
    
  
         
  

12. D E T A L L E D E L A R M A D O D E C O L U M N A Y Z A P A T A