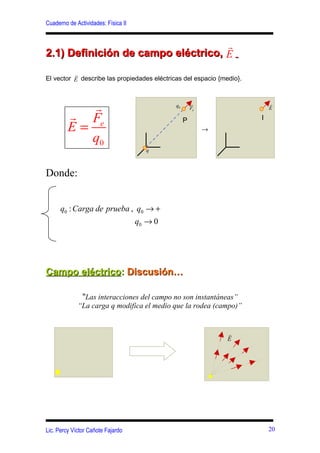
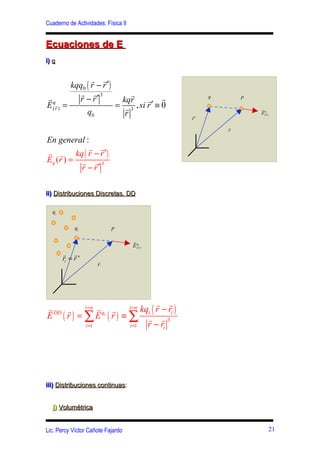
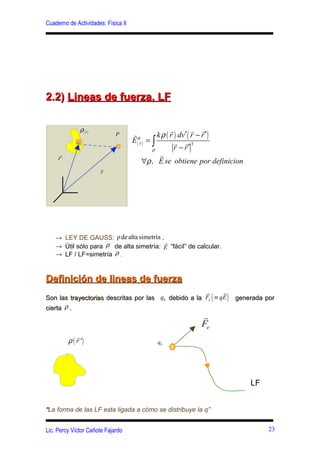
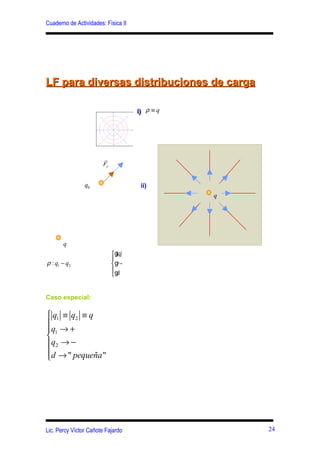
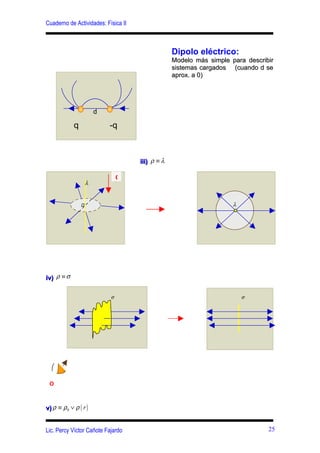
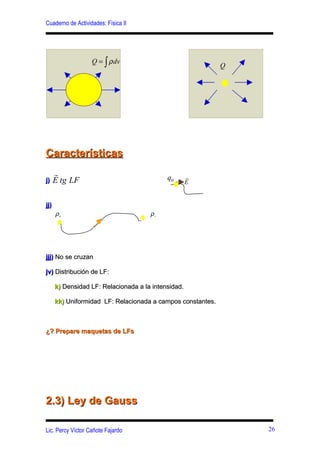
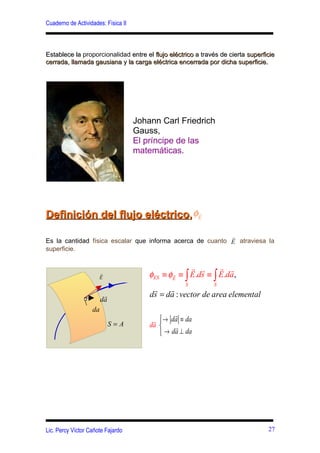
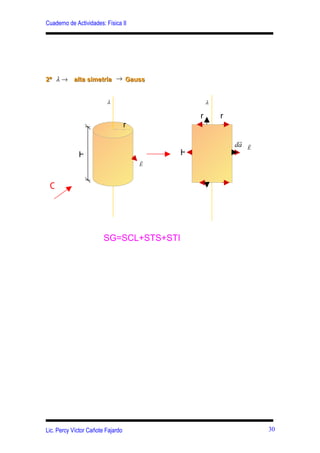
Este documento presenta conceptos clave sobre el campo eléctrico y la ley de Gauss, incluyendo: (1) la definición del campo eléctrico y sus ecuaciones para diferentes distribuciones de carga, (2) la introducción de las líneas de fuerza eléctricas y sus características para varias distribuciones de carga, y (3) la definición del flujo eléctrico y la formulación matemática de la ley de Gauss.