CENTRO DE MASA O GRAVEDAD

INTRODUCCIÓN
En este trabajo
buscamos dar a
conocer las
utilidades de la
derivada aplicada
a la física.
 Que tiene como tema
principal el centro de
masa. El centro de
masa de un objeto
se deriva de la
posición del punto de
la posición del centro
de gravedad.

Definición
 Es el punto donde
puede considerarse
que está concentrada
toda la masa de un
cuerpo para estudiar
determinados
aspectos de su
movimiento.
 Para tratar de
comprender y calcular
el movimiento de un
objeto, suele resultar
más sencillo fijar la
atención en el centro
de masa.

PROPIEDADES DEL CENTRO DE
GRAVEDAD

Un objeto apoyado
sobre una base
plana estará en
equilibrio estable si
la vertical que pasa
por el centro de
gravedad corta a la
base de apoyo
 El centro de gravedad puede
caer fuera de la base de
apoyo y, en estas
condiciones, no habrá un
momento restaurador y el
cuerpo abandona
definitivamente la posición de
equilibrio inicial mediante
una rotación que le llevará a
una nueva posición de
equilibrio.

Cálculo del centro de gravedad
 El centro de gravedad de un cuerpo
viene dado por el único vector que
cumple que:
Donde M es la masa total del cuerpo y x
denota el producto vectorial.

 En un campo gravitatorio
uniforme, es decir, uno en
que el vector de campo
gravitatorio g es el mismo
en todos los puntos, la
definición anterior se
reduce a la definición del
centro de masas:
 En el campo gravitatorio
creado por un cuerpo material
cuya distancia al objeto
considerado sea muy grande
comparado con las
dimensiones del cuerpo y del
propio objeto, el centro de
gravedad del objeto viene
dado por:

MÉTODO DE INTEGRACIÓN DIRECTA:
 Para calcular el centroide de una figura
plana que está limitada por arriba por la
función “f(x)” , por debajo por la función
“g(x)”, por la izquierda por la recta “X = a”
y por la derecha por la recta “X = b”; se
utilizan las siguientes fórmulas :
Donde “A” representa el área de
la figura plana a la que se le está
calculando el centroide.

EJERCICIOS RESUELTOS
 Ejercicio 1: Calcular la ubicación del Centroide
de la región acotada por “Y = X2” y “Y = X”
 Solución:
 El primer paso consiste en graficar las dos
funciones para determinar cuál queda ubicada
arriba y cuál debajo. Igualmente se deben
calcular los puntos de intersección de las dos
funciones para conocer los índices superior e
inferior de la integral definida.

 Una vez hecha la gráfica
podemos decir que:
 f(x) = “Y = X”
 g(x) = “Y = X2”
 a = 0
 b = 1
 Calculando el área de la región
acotada:

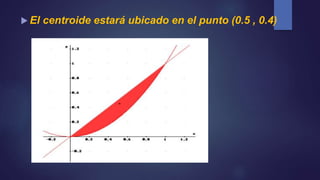
 El centroide estará ubicado en el punto (0.5 , 0.4)

 Ejercicio 2: Calcular la ubicación del Centroide de la región acotada
por “f (x)= 4-x2 “ y “g (x)= x+2” :
 Solución:
 El primer paso consiste en graficar las dos funciones para determinar
cuál queda ubicada arriba y cuál debajo. Igualmente se deben calcular
los puntos de intersección de las dos funciones para conocer los
índices superior e inferior de la integral definida.
Estas 2 curvas se cortan en (-2,0) y en (1,3),
por lo que el área es:

El centroide es: (-1/2,12/5)
El centroide es: (-0.5 , 2.4)

 Ejercicio 3: Calcular la ubicación del Centroide de la región
acotada por “Y = X2” y “Y = 8 – X2”
Como apuntamos al inicio de esta guía: Si una figura
geométrica posee un eje de simetría, el centroide de la
figura coincide con este eje.
Esta figura en particular posee un eje de simetría
horizontal y un eje de simetría vertical, luego su
centroide estará ubicado en el punto de intersección de
sus dos ejes de simetría.
Se recomienda que utilice los procedimientos explicados en
los dos ejercicios anteriores y verifique la ubicación del
centroide de la figura.

CENTRO DE MASA O GRAVEDAD

Más contenido relacionado

La actualidad más candente

Similar a CENTRO DE MASA O GRAVEDAD

Último

CENTRO DE MASA O GRAVEDAD