Este documento describe el cálculo de integrales dobles. Explica que una integral doble integra una función de dos variables sobre una región del plano, manteniendo una variable fija e integrando respecto a la otra. También cubre temas como los límites de integración, el teorema de Fubini y el uso del determinante jacobiano para realizar cambios de variable en integrales dobles.

1. Integrales dobles

2. La integral doble
 


R
ΔA
n
lim
1j
)jy,jf (x
n
y )dAf (x,
Sea f, continua en una región R del plano xy . Usando líneas paralelas a los ejes
para aproximar R por medio de n rectángulos de área A. Sea (xj,yj) un pto del j-
esimo rectángulo, entonces la integral doble de f sobre R es:
( xJ, xj+1)

3.  La integral doble es integrar funciones de dos variables f(x;y) para lo cual se emplearán las
mismas técnicas que se utilizaron en la evaluación de las Integrales simples. Sin embargo,
como se incluyen dos variables, se debe integrar f(x;y) manteniendo una variable fija e
integrando respecto a la otra.

4. La integral doble de f sobre la región R, está dada por el valor común de las dos
integrales iteradas.
Donde a, b, c y d son los límites de integración de la región R.
Para resolver la integral doble, se mantiene fija una variable y se integra con
respecto a la otra variable.
Cálculo de integrales dobles
   
b
a
d
c
d
c
b
a
R
y )dy dxf (x,y )dxdyf (x,y )dAf (x,

5. Propiedades
 
RR
y )dAf (x,Ky )dAK.f (x,a)
   
R RR
y )dAg(x,y )dAf (x,y )dAg(x,y )f (x,b)
 
R
0y )dAf (x,Ry )(x,0,y )f (x,Sic) ,
  


1 2R RR
y )dAf (x,y )dAf (x,y )dAf (x,
sobreponenseno2Ry1Rdonde,2R1RRSid)

6. Límites de integración
Secciones transversales verticales: Una figura horizontal implica el orden dydx, si
la región R está limitada por las gráficas de g1 y g2 en el intervalo [a, b]. Si R es
descrita por
R: a  x  b , g1(x)  y  g2(x)
y = g1(x)
y = g2(x)
a b
R
  
b
a
(x)g
(x)g
R
2
1
y )dy dxf (x,y )dAf (x,

7. Límites de integración
Secciones transversales horizontales: Una figura vertical implica el orden dxdy, si
la región R está limitada por las gráficas de h1 y h2 en el intervalo [c, d]. Si R es
descrita por
R: c  y  d , h1(y)  x  h2(y)
x = h1(x)
x = h2(x)
c
d
R
  
d
c
(y)h
(y)h
R
2
1
y )dxdyf (x,y )dAf (x,

8. Área de una región rectangular
))(( abcddydx
c
d
a
b

 dxy
a
b
dydx
c
d
a
b d
c 
dxcd
a
b
)(  
 b
axcd )( 
))(( abcd 

9. Calcular la integral de una integral o integral doble :
dxdyyyx
x







 )22(
11
2 22
 2
1
23
xxx  )1(2  3
dxyyx x
1
212
)]2(
1
2
 







 dxdyyyx
x
)22(
11
2 22
dxxx )132(
1
2 2
 -2x2(x-1)+x2-(-2x21-1+1)

10. Comparación de distinta forma de Integración
• Graficando el área de una región dado por la integral:
• Nos fijamos en los limites de la integración, vemos que.
y^2 ≤ x ≤ 4 (Limites interiores de integración)
• De modo que el área de la región esta acotada a la izquierda por la parábola x = y^2
y a la derecha por la recta x = 4. Además notamos que.
0 ≤ y ≤ 2 (Limites exteriores de integración)
∫ 2
Y^2
∫0
4
∂x∂y

11. Resolviendo las integrales:
∫
= 16 / 3
 Entonces el valor de esta integral se vera de la siguiente forma:
0
2
Y^2
4
∫ ∂x ∂y = ∫
2
0
x ]
4
Y^2
∂y
=
2
∫0
(4 – y^2) ∂y
4y – (y^3)/(3)]=
2
0

12. (4,2)
1 42 3
1
2
3
4 X = Y^2
ΔY
X
Y
AREA = ∫ 2
0
∫ Y^2
4
∂x . ∂y
0

13. Cambiando el orden de la integración: ∂y ∂x
 En este caso los limites de las variables “x” ; “y” cambiaran en la integración.
Si despejamos “y” :
x = y^2  y= x^(1/2)
 Concluimos que los limites interiores de integración serán:
0 ≤ y ≤ x^(1/2)
 Ahora en nuestra grafica el rectángulo horizontal cambiara en forma vertical.
 Por lo tanto las cotas varían en el intervalo:
0 ≤ x ≤ 4
 Sera un limite exterior de integración.

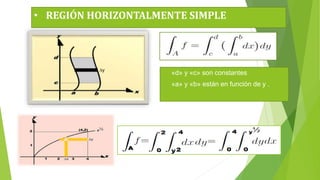
14. • Por lo tanto el área de la región se puede representar por:

 Calculando la integral comprobaremos que da el mismo valor que la integral original.
4
∫0
∫
X^1/2
0
∂x ∂y
∫ 0
4
∫
0
X^1/2
∂y ∂x =
4 X^1/2
∫ 0
Y]0
∂x
= ∫0
4
x^1/2 ∂x
16 / 3
0
4
](2/3)*x^3/2=
=
2

15. (4,2)
1 42 3
1
2
3
4
Y
X
ΔX
Y = X^1/2
AREA =∫
4
0
∫ 0
X^1/2
. ∂x∂y
0

16. TEOREMA FUBINI
Si “R”(región) es verticalmente simple u
horizontalmente simple, y si “f” es continua
en “R” (región), la integral doble de “f”
sobre “R” es igual a la integral iterada.
dx dy ↔ dy dx

17. REGION VERTICALMENTE Y
HORIZONTALMENTE SIMPLE
 REGIÓN VERTICALMENTE SIMPLE
• «a» y «b» son constantes
• «c» y «d» están en función de x ;en
donde d > c .
∆x

18. • REGIÓN HORIZONTALMENTE SIMPLE
 «d» y «c» son constantes
 «a» y «b» están en función de y .
∆y

19. FUBINI :
Si estas funciones son integrables, sus integrales se escribirían:
• Donde x es una constante, y la variable es y ϵ A2.
• Donde y es una constante y la variable es x ϵ A1.

20. EJEMPLO:
Hallar el volumen de la región R acotada por 0 ≤ x ≤ 1; 0 ≤ y ≤ 1 de la
función 1-(1/2)x² -(1/2)y² .

22. Introducción.
 Es útil para reducir la complejidad de la integral ,
cambiar una variable por otra resulte mas cómoda, sin
embargo esto exige el cambio de la región de
integración, además de añadir un factor de corrección
al diferencial conocido como determinante jacobiano.

23. Definición
Sean R y S regiones en los planos 𝒙𝒚 𝒚 𝒖𝒗 relacionadas por las ecuaciones𝒙 =
𝒈 𝒖, 𝒗 𝒆 𝒚 = 𝒉 𝒖, 𝒗 , tales que cada punto de R es imagen de un único punto de
S. si f es continua en R, g y h tienen derivadas parciales continuas en S,
𝝏 𝒙,𝒚
𝝏 𝒖,𝒗
Es no nula en S, entonces:
𝑹
𝒇 𝒙, 𝒚 𝒅𝒙. 𝒅𝒚 =
𝑺
𝒇 𝒈 𝒖, 𝒗 , 𝒉 𝒖, 𝒗 ⎜
𝒅 𝒙, 𝒚
𝒅 𝒖, 𝒗
⎜. 𝒅𝒖 𝒅𝒗

24.  En una integral simple
𝒂
𝒃
𝒇 𝒙 . 𝒅𝒙
Podemos cambiar de variable haciendo 𝒙 = 𝒈 𝒖 , con lo que 𝒅𝒙 =
𝒈° 𝒖 𝒅𝒖, 𝒚 𝒐𝒃𝒕𝒆𝒏𝒆𝒎𝒐𝒔
𝒂
𝒃
𝒇 𝒙 𝒅𝒙 = 𝒄
𝒅
𝒇 𝒈 𝒖 𝒈° 𝒖 𝒅𝒖
Donde a=g(c) y b=g (d). Nótese que el cambio de variable introduce un factor
adicional g°(u) en el integrando. Lo mismo ocurre en el caso de las integrales
dobles. jacobiano
𝑹 𝒇 𝒙, 𝒚 𝒅𝑨 = 𝒔 𝒇 𝒈 𝒖, 𝒗 , 𝒉 𝒖, 𝒗
𝒅𝒙
𝒅𝒖
𝒅𝒚
𝒅𝒗
−
𝒅𝒚
𝒅𝒖
𝒅𝒙
𝒅𝒗
dudv
Donde el cambio de variable 𝒙 = 𝒈 𝒖, 𝒗 , 𝒚 = 𝒖, 𝒗 introduce un factor que se
llama el jacobiano de 𝒙, 𝒚 respecto de 𝒖, 𝒗. Al definir el jacobiano conviene utilizar
la siguiente notación en términos de determinantes.

25. Definición del jacobiano.
Si 𝒙 = 𝒈 𝒖, 𝒗 𝒆 𝒚 = 𝒉(𝒖, 𝒗), el jacobiano de 𝒙, 𝒚 𝒓𝒆𝒔𝒑𝒆𝒄𝒕𝒐 𝒖, 𝒗, que se denota por el
símbolo
𝝏(𝒙,𝒚)
𝝏(𝒖,𝒗)
, es:
𝝏 𝒙,𝒚
𝝏(𝒖,𝒗)
= ⎜
𝒅𝒙/𝒅𝒖 𝒅𝒙/𝒅𝒗
𝒅𝒚/𝒅𝒖 𝒅𝒚/𝒅𝒗
⎜=
𝒅𝒙.𝒅𝒚
𝒅𝒖 𝒅𝒗
-
𝒅𝒚.𝒅𝒙
𝒅𝒖 𝒅𝒗
Problemas:
Calcular 𝑹
(𝒙 + 𝒚 + 𝟏)𝒅𝑨 , donde R es la región limitada por las rectas :
Y-x=1, y-x=-1, x+y=1 y x+y= 2
solución:
 Y-x =u y x+y=v
 J(u,v)=
𝟏
𝑱 𝒙,𝒚

26.  J(x, y)=det⎜
𝑑𝑢/𝑑𝑥 𝑑𝑢/𝑑𝑦
𝑑𝑣/𝑑𝑥 𝑑𝑣/𝑑𝑦
⎜ = 𝑑𝑒𝑡⎜
−1 1
1 1
⎜ = −2
v
y 2

-- 1
------
--------
-- x -1 1 u

27. 𝒙 + 𝒚 + 𝟏 𝒅𝑨
J(x,y) = -2
J(u,v) =
𝟏
𝑱(𝒙,𝒚)
= -
𝟏
𝟐
 𝟏
𝟐
( −𝟏
𝟏
𝒗 + 𝟏 ⎜ −
𝟏
𝟐
⎜𝒅𝒖)𝒅𝒗
1

𝟏
𝟐 −𝟏
𝟏
𝒗 + 𝟏 𝒅𝒖 =
𝟏
𝟐
(uv+u ) =
𝟏
𝟐
( 𝒗 + 𝟏 − −𝒗 − 𝟏 )
-1 =v+1
2
 𝟏
𝟐
𝒗 + 𝟏 𝒅𝒗 =(
𝒗 𝟐
𝟐
+ 𝐯) = (
𝟐 𝟐
𝟐
+2) –(
𝟏 𝟐
𝟐
+ 𝟐)
1
=
𝟓
𝟐

28. Conclusiones:
 Al resolver los ejercicios de integrales dobles
obtenemos como resultado, que el uso de la función
jacobiana y el cambio de variable reduce la dificultad
de los ejercicios.