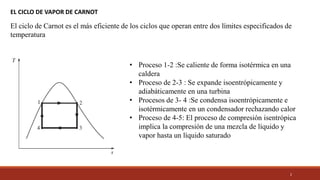
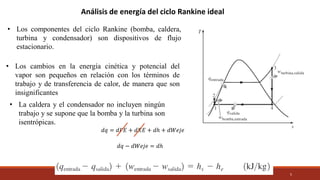
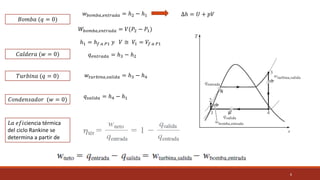
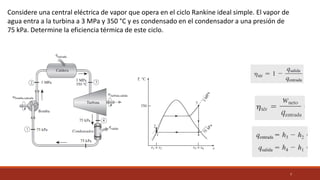
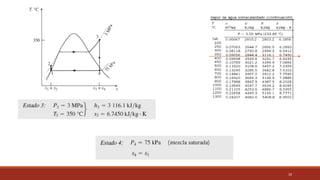
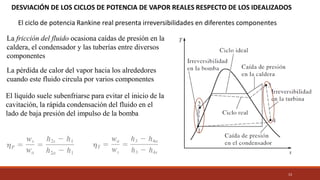
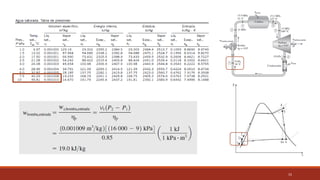
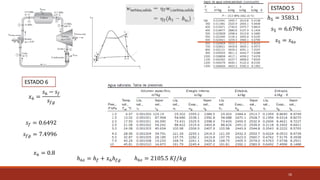
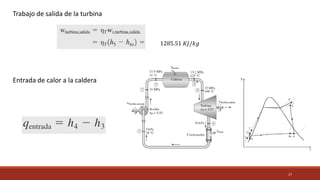
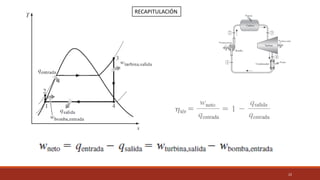
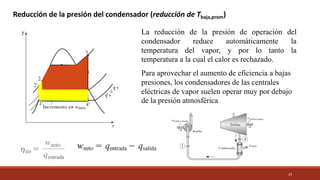
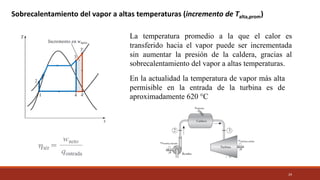
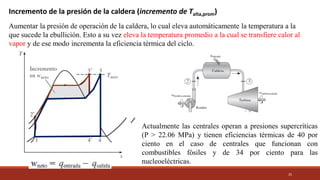
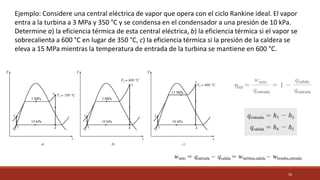
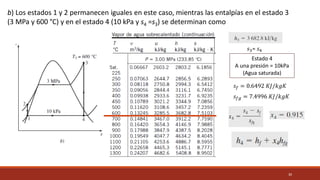
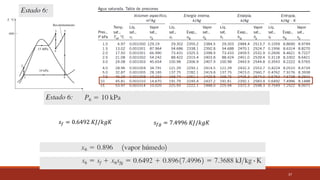
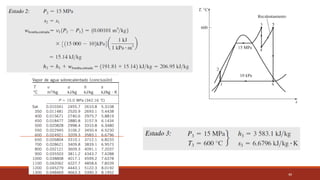
El documento detalla el ciclo Rankine, ideal para procesos de generación de energía en centrales térmicas, describiendo sus cuatro procesos principales y análisis de eficiencia térmica. Se discuten las diferencias entre ciclos ideales y reales, así como estrategias para incrementar la eficiencia térmica, como el aumento de presión y temperatura del vapor. Además, se presentan ejemplos prácticos de cálculos de eficiencia térmica y el impacto del recalentamiento del vapor en la operación de turbinas.

1. 1
Escuela Superior Politécnica de Chimborazo
FACULTAD DE MECÁNICA CARRERA DE INGENIERÍA INDUSTRIAL
Asignatura: Termodinámica
CICLO RANKINE
Profesora: Ing. Daniela Vásconez Núñez Ph.D.

2. 2
EL CICLO DE VAPOR DE CARNOT
El ciclo de Carnot es el más eficiente de los ciclos que operan entre dos límites especificados de
temperatura
• Proceso 1-2 :Se caliente de forma isotérmica en una
caldera
• Proceso de 2-3 : Se expande isoentrópicamente y
adiabáticamente en una turbina
• Procesos de 3- 4 :Se condensa isoentrópicamente e
isotérmicamente en un condensador rechazando calor
• Proceso de 4-5: El proceso de compresión isentrópica
implica la compresión de una mezcla de líquido y
vapor hasta un líquido saturado

3. 3
CICLO RANKINE: EL CICLO IDEAL PARA LOS CICLOS DE POTENCIA DE VAPOR
Es el ciclo ideal para las centrales térmicas de vapor.
El ciclo Rankine ideal no incluye ninguna irreversibilidad interna y está compuesto por cuatro procesos

4. 4

5. 5
Análisis de energía del ciclo Rankine ideal
• Los componentes del ciclo Rankine (bomba, caldera,
turbina y condensador) son dispositivos de flujo
estacionario.
• Los cambios en la energía cinética y potencial del
vapor son pequeños en relación con los términos de
trabajo y de transferencia de calor, de manera que son
insignificantes
• La caldera y el condensador no incluyen ningún
trabajo y se supone que la bomba y la turbina son
isentrópicas.
𝑑𝑞 = 𝑑𝑃𝐸 + 𝑑𝐾𝐸 + 𝑑ℎ + 𝑑𝑊𝑒𝑗𝑒
𝑑𝑞 − 𝑑𝑊𝑒𝑗𝑒 = 𝑑ℎ

6. 6
𝑊𝑏𝑜𝑚𝑏𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 𝑉(𝑃2 − 𝑃1)
ℎ1 = ℎ𝑓 𝑎 𝑃1 𝑦 𝑉 ≅ 𝑉1 = 𝑉𝑓 𝑎 𝑃1
𝐶𝑎𝑙𝑑𝑒𝑟𝑎 (𝑤 = 0)
𝑇𝑢𝑟𝑏𝑖𝑛𝑎 (𝑞 = 0)
𝐶𝑜𝑛𝑑𝑒𝑛𝑠𝑎𝑑𝑜𝑟 (𝑤 = 0)
𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = ℎ3 − ℎ2
𝑤𝑡𝑢𝑟𝑏𝑖𝑛𝑎,𝑠𝑎𝑙𝑖𝑑𝑎 = ℎ3 − ℎ4
𝑞𝑠𝑎𝑙𝑖𝑑𝑎 = ℎ4 − ℎ1
𝐿𝑎 𝑒𝑓𝑖ciencia térmica
del ciclo Rankine se
determina a partir de
𝐵𝑜𝑚𝑏𝑎 (𝑞 = 0)
𝑤𝑏𝑜𝑚𝑏𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = ℎ2 − ℎ1 ∆ℎ = 𝑈 + 𝑝𝑉

7. 7
Considere una central eléctrica de vapor que opera en el ciclo Rankine ideal simple. El vapor de
agua entra a la turbina a 3 MPa y 350 °C y es condensado en el condensador a una presión de
75 kPa. Determine la eficiencia térmica de este ciclo.

8. 8

9. 9
𝑊𝑏𝑜𝑚𝑏𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 𝑉(𝑃2 − 𝑃1)
𝑤𝑏𝑜𝑚𝑏𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = ℎ2 − ℎ1

10. 10

11. 11

12. 12
Esta central eléctrica convierte en trabajo neto 26 por ciento del calor que recibe de la caldera

13. 13
DESVIACIÓN DE LOS CICLOS DE POTENCIA DE VAPOR REALES RESPECTO DE LOS IDEALIZADOS
El ciclo de potencia Rankine real presenta irreversibilidades en diferentes componentes
La fricción del fluido ocasiona caídas de presión en la
caldera, el condensador y las tuberías entre diversos
componentes
La pérdida de calor del vapor hacia los alrededores
cuando este fluido circula por varios componentes
El líquido suele subenfriarse para evitar el inicio de la
cavitación, la rápida condensación del fluido en el
lado de baja presión del impulso de la bomba

14. 14
Una central eléctrica de vapor opera en el ciclo que se muestra en la figura. Si las eficiencias
isentrópicas de la turbina y la bomba son de 87 por ciento y de 85 por ciento, respectivamente,
determine a) la eficiencia térmica del ciclo y b) la salida de potencia neta de la central para un
flujo másico de 15 kg/s.

15. 15

16. 16
ℎ5 = 3583.1
𝑠5 = 𝑠6𝑠
𝑥6 =
𝑠6 − 𝑠𝑓
𝑠𝑓𝑔
ℎ6𝑠 = ℎ𝑓 + 𝑥6ℎ𝑓𝑔
𝑠5 = 6.6796
𝑠𝑓 = 0.6492
𝑠𝑓𝑔 = 7.4996
𝑥6 = 0.8
ℎ6𝑠 = 2105.5 𝐾𝐽/𝑘𝑔
ESTADO 6
ESTADO 5

17. 17
Trabajo de salida de la turbina
Entrada de calor a la caldera
1285.51 𝐾𝐽/𝑘𝑔

18. 18
T hP15 hP20
20 97.93 102.57
35 h(15) h(20)
40 180.77 185.16
P (T=35ºC) h
15 h(15)
15.9 hP15.9
20 h(20)
P h
15 160.06
15.9 hP15.9
20 164.51
ℎ3 = 160.86
𝑃𝑈𝑁𝑇𝑂 3

19. 19
𝐸𝑆𝑇𝐴𝐷𝑂 4

20. 20
Entrada de calor a la caldera
𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 3646 − 160.18 = 3485.14 𝐾𝐽/𝑘𝑔
Trabajo neto
Eficiencia térmica
𝑛𝑡é𝑟 =
𝑊𝑛𝑒𝑡𝑜
𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎
1266.51 𝐾𝐽/𝑘𝑔
3485.14 𝐾𝐽/𝑘𝑔
= 0.363 → 36.3%
La potencia neta producida por la central
1285.51 − 19 = 1266.51 𝐾𝐽/𝑘𝑔

21. 21
¿CÓMO INCREMENTAR LA EFICIENCIA DEL CICLO RANKINE?
Cualquier incremento en la eficiencia térmica pueden significar grandes ahorros en los
requerimientos de combustible.
• Incrementar la temperatura promedio a la que el calor se transfiere al fluido de
trabajo en la caldera.
• Disminuir la temperatura promedio a al que el calor se rechaza del fluido de trabajo
en el condensador
Tres manera de lograrlo:
• Reducción de la presión del condensador (reducción de Tbaja,prom)
• Sobrecalentamiento del vapor a altas temperaturas (incremento de Talta,prom )
• Incremento de la presión de la caldera (incremento de Talta,prom )

22. 22
RECAPITULACIÓN

23. 23
La reducción de la presión de operación del
condensador reduce automáticamente la
temperatura del vapor, y por lo tanto la
temperatura a la cual el calor es rechazado.
Para aprovechar el aumento de eficiencia a bajas
presiones, los condensadores de las centrales
eléctricas de vapor suelen operar muy por debajo
de la presión atmosférica
Reducción de la presión del condensador (reducción de Tbaja,prom)

24. 24
La temperatura promedio a la que el calor es
transferido hacia el vapor puede ser incrementada
sin aumentar la presión de la caldera, gracias al
sobrecalentamiento del vapor a altas temperaturas.
En la actualidad la temperatura de vapor más alta
permisible en la entrada de la turbina es de
aproximadamente 620 °C
Sobrecalentamiento del vapor a altas temperaturas (incremento de Talta,prom)

25. 25
Incremento de la presión de la caldera (incremento de Talta,prom)
Aumentar la presión de operación de la caldera, lo cual eleva automáticamente la temperatura a la
que sucede la ebullición. Esto a su vez eleva la temperatura promedio a la cual se transfiere calor al
vapor y de ese modo incrementa la eficiencia térmica del ciclo.
Actualmente las centrales operan a presiones supercríticas
(P > 22.06 MPa) y tienen eficiencias térmicas de 40 por
ciento en el caso de centrales que funcionan con
combustibles fósiles y de 34 por ciento para las
nucleoeléctricas.

26. 26
Ejemplo: Considere una central eléctrica de vapor que opera con el ciclo Rankine ideal. El vapor
entra a la turbina a 3 MPa y 350 °C y se condensa en el condensador a una presión de 10 kPa.
Determine a) la eficiencia térmica de esta central eléctrica, b) la eficiencia térmica si el vapor se
sobrecalienta a 600 °C en lugar de 350 °C, c) la eficiencia térmica si la presión de la caldera se
eleva a 15 MPa mientras la temperatura de entrada de la turbina se mantiene en 600 °C.

27. 27
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾
ℎ𝑓 = 191.81 𝐾𝐽/𝑘𝑔
a) la eficiencia térmica de esta central eléctrica
ESTADO 4
𝑊𝑏𝑜𝑚𝑏𝑎 = ℎ2 − ℎ1
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾
ℎ𝑓𝑔 = 2392.1 𝐾𝐽/𝑘𝑔

28. 28
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾
𝑠𝑓𝑔 = 7.4996 𝐾𝐽/𝑘𝑔𝐾
𝑠3= 𝑠4
𝑠4 = 𝑆𝑓 + 𝑥4𝑆𝑓𝑔

29. 29

30. 30
b) Los estados 1 y 2 permanecen iguales en este caso, mientras las entalpías en el estado 3
(3 MPa y 600 °C) y en el estado 4 (10 kPa y s4 =s3) se determinan como
𝑠3= 𝑠4
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾
𝑠𝑓𝑔 = 7.4996 𝐾𝐽/𝑘𝑔𝐾
Estado 4
A una presión = 10kPa
(Agua saturada)

31. 31
La eficiencia térmica aumenta de 33.4 a 37.3 por ciento como resultado de sobrecalentar el vapor
de 350 a 600°C.
Al mismo tiempo, la calidad del va por aumenta de 81.3 a 91.5 por ciento

32. 32
c) El estado 1 permanece igual en este caso, aunque los otros estados cambien. Las entalpías en los
estados 2 (15 MPa y s2 = s1), 3 (15 MPa y 600 °C) y 4 (10 kPa y s4 =s3) se determinan de manera
similar como
𝑠3= 𝑠4
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾
𝑠𝑓𝑔 = 7.4996 𝐾𝐽/𝑘𝑔𝐾

33. 33
La eficiencia térmica aumenta de 37.3 a 43.0 por ciento como consecuencia de elevar la presión
de la caldera de 3 a 15 MPa mientras se mantiene en 600 °C la temperatura a la entrada de la
turbina.
Sin embargo, al mismo tiempo la calidad del vapor disminuye de 91.5 a 80.4 por ciento (en otras
palabras, el contenido de humedad aumenta de 8.5 a 19.6 por ciento

34. 34
EL CICLO RANKINE IDEAL CON RECALENTAMIENTO
La presión de la caldera incrementa la eficiencia térmica del ciclo Rankine, pero que también incrementa
el contenido de humedad del vapor a niveles inaceptables.
1. Sobrecalentar el vapor a
temperaturas muy altas antes de que
entre a la turbina. → Ésta sería la
solución deseable porque la
temperatura promedio a la que se añade
calor también se incrementaría, lo cual
aumentaría la eficiencia del ciclo.
2. Expandir el vapor en la turbina en dos etapas y recalentarlo entre ellas.
El recalentamiento es una solución práctica al problema de humedad excesiva en turbinas y es comúnmente
utilizada en modernas centrales eléctricas de vapor.

35. 35
El único propósito del ciclo de recalentamiento es reducir el contenido de humedad del vapor en las
etapas finales del proceso de expansión.
Si se contara con materiales que soportaran temperaturas suficientemente altas, no habría necesidad del
ciclo de recalentamiento.

36. 36
Una central eléctrica de vapor que opera en el ciclo Rankine ideal con recalentamiento. El vapor entra a la turbina de
alta presión a 15 MPa y 600 °C y se condensa a una presión de 10 kPa. Si el contenido de humedad del vapor a la salida
de la turbina de baja presión no excede 10.4 porciento, determine a) la presión a la que el vapor se debe recalentar y b)
la eficiencia térmica del ciclo. Su ponga que el va por se recalienta hasta la temperatura de
entrada de la turbina de alta presión.
𝑠5 = 𝑠6
𝑇5

37. 37
𝑠𝑓 = 0.6492 𝐾𝐽/𝑘𝑔𝐾 𝑠𝑓𝑔 = 7.4996 𝐾𝐽/𝑘𝑔𝐾

38. 38
Por lo tanto, el vapor debe recalentarse a una presión de 4 MPa o menor para evitar un contenido
de humedad superior a 10.4 por ciento.
𝑠5 = 7.3688 𝐾𝐽/𝑘𝑔𝐾 𝑇5 = 600 º𝐶

39. 39
b) Para determinar la eficiencia térmica, es necesario saber las entalpías en todos los demás estados:

40. 40

41. 41
T h S
350 3093.3 6.5843
TX hX 6.6796
400 3214.5 6.7714

42. 42

43. 43
BÁSICA
Cengel, Y., Boles, M. (2015). Termodinámica. (8ª ed.) México D.F., México: McGraw-Hill. Disponible en la biblioteca de Mecánica
Disponible en la biblioteca de Mecánica
Moran, M. J. y Shapiro, H. N. (2015). Fundamentos de termodinámica técnica (2a. ed.). Barcelona, España: Editorial Reverté. Recuperado de
https://elibro.net/es/ereader/espoch/46771.
Disponible en la biblioteca virtual E-libro.
COMPLEMENTARIA
Barbosa Saldaña, J. G., Gutiérrez Torres, C. C. y Jiménez Bernal, J. A. (2015). Termodinámica para ingenieros. México, México: Grupo Editorial Patria.
Recuperado de https://elibro.net/es/ereader/espoch/40432.
Disponible en la biblioteca virtual E-libro.
Rolle, K. C. (2006). Termodinámica. Naucalpan de Juárez, México: Pearson Educación. Recuperado de https://elibro.net/es/ereader/espoch/74113.
Disponible en la biblioteca virtual E-libro.
Broatch Jacobi, A., Galindo Lucas J. y Payri Marín R. (2013). Problemas de ingeniería térmica. Valencia, España: Editorial de la Universidad Politécnica de
Valencia. Recuperado de https://elibro.net/es/ereader/espoch/54058.
Disponible en la biblioteca virtual E-libro.
Del Barrio, M. Bravo, E. y Lana, F. (2006). Termodinámica básica: ejercicios. Universitat Politècnica de Catalunya. https://elibro.net/es/ereader/espoch/61437.
Disponible en la biblioteca virtual E-libro.
Golden, M. (2011). Termodinámica para ingeniería. México D. F., México: Trillas.
Disponible en la biblioteca de Mecánica
BIBLIOGRAFÍA