El documento describe tres diseños de circuitos resonantes. El primero es un circuito resonante en paralelo con Rs=RL. El segundo es similar pero con Rs ≠ RL, por lo que se usa un circuito de acoplo tapped C. El tercero usa dos circuitos resonantes idénticos acoplados mediante un inductor.









![REFERENCIAS
[1] NI AWR Design Environment (14.0). (2018). [Software de Ordenador]. National
Instruments. https://www.awr.com/
[2] Briceño. E (2022) Emisores y Receptores [Diapositiva Power Point]. Disponible En
Cavas UTPL.
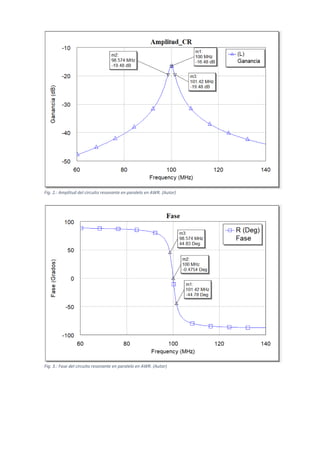
Fig. 8: Amplitud de un circuito resonante acoplado mediante un inductor con un circuito de acoplo Tapped C en AWR.
(Autor)](https://image.slidesharecdn.com/annotated-tarea21b-220828151513-0c644201/85/Circuitos-resonantes-11-320.jpg)