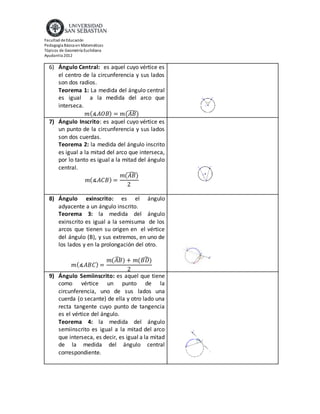
El documento describe los elementos básicos de la circunferencia como el centro, radio, cuerda, diámetro, arco, recta tangente y secante. Explica 11 propiedades de las circunferencias relacionadas con ángulos centrales, inscritos, exinscritos, semiinscritos, interiores y exteriores, y cómo se relacionan con los arcos. Finalmente, presenta 6 ejercicios prácticos para aplicar estos conceptos.

1. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
Guía de Aprendizaje N°2
Elementos y Propiedades de la Circunferencia
Definición: Una circunferencia es el conjunto de puntos en el plano que equidistan de un
punto fijo. El punto fijo se llama centro de la circunferencia.
Radio: es un segmento determinado por el centro de la circunferencia y un punto
cualquiera de ella. El segmento OP es un radio de la circunferencia, los radios se denotan
generalmente por la letra “r”.
Cuerda: es un segmento determinado por dos puntos de la circunferencia. El diámetro es
la cuerda que contiene al centro de la circunferencia. Es la cuerda de mayor longitud, en
una circunferencia existen infinitos diámetros.
𝑨𝑷̅̅̅̅, diámetro de la circunferencia.

2. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
Arco: es una parte continua de la circunferencia, se mide en grados o radianes y se
determina por puntos en la circunferencia. 𝐴𝐵̂ es un arco de la circunferencia. Cuando un
arco es menor a 180° o es contenido por un ángulo central, este es denotado por dos
puntos si es mayor a 180°, entonces es denotado por tres puntos.
En la figura arco 𝐴𝐵̂ y arco 𝐴𝐶𝐵̂
Recta Tangente: es la recta que interseca exactamente punto de una circunferencia. El
punto de intersección se llama punto de tangencia.
En la figura la recta L es tangente a la circunferencia de centro O en el punto T. entre el
punto de tangencia y el centro de la circunferencia el radio es perpendicular a la recta.
Recta Secante: es la recta que interseca a la circunferencia en dos puntos. La recta L es
secante a la circunferencia de centro O en los puntos A y B.

3. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
Propiedades de las circunferencias:
1) Si dos cuerdas son congruentes, entonces
los arcos determinados por ella son
congruentes:
Si 𝐴𝐵̅̅̅̅ ≅ 𝐷𝐸̅̅̅̅ entonces 𝐴𝐵̂ ≅ 𝐷𝐸̂
2) Si dos cuerdas son congruentes, entonces
los puntos medios de ellas equidistan del
centro y son perpendiculares al centro de
la circunferencia.
3) Si dos cuerdas de una circunferencia son
paralelas, los arcos comprendidos por
ellas son congruentes.
Si 𝐴𝐵̅̅̅̅ ∥ 𝐶𝐷̅̅̅̅, entonces 𝐴𝐵̂ ≅ 𝐶𝐷̂
4) Todo diámetro perpendicular a una
cuerda, lo dimidia y también dimidia los
arcos determinados por ella.
Si 𝐴𝐵̅̅̅̅ ⊥ 𝐶𝐷̅̅̅̅, entonces M, punto medio
de 𝐶𝐷̅̅̅̅
5) Si L y M son rectas que pasan por el
punto C y son tangentes a la
circunferencia de centro O en los puntos
A y B, entonces los segmentos AC̅̅̅̅y BC̅̅̅̅
son congruentes.

4. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
6) Ángulo Central: es aquel cuyo vértice es
el centro de la circunferencia y sus lados
son dos radios.
Teorema 1: La medida del ángulo central
es igual a la medida del arco que
interseca.
𝑚(∡𝐴𝑂𝐵) = 𝑚(𝐴𝐵)̂
7) Ángulo Inscrito: es aquel cuyo vértice es
un punto de la circunferencia y sus lados
son dos cuerdas.
Teorema 2: la medida del ángulo inscrito
es igual a la mitad del arco que interseca,
por lo tanto es igual a la mitad del ángulo
central.
𝑚(∡𝐴𝐶𝐵) =
𝑚(𝐴𝐵)̂
2
8) Ángulo exinscrito: es el ángulo
adyacente a un ángulo inscrito.
Teorema 3: la medida del ángulo
exinscrito es igual a la semisuma de los
arcos que tienen su origen en el vértice
del ángulo (B), y sus extremos, en uno de
los lados y en la prolongación del otro.
𝑚(∡𝐴𝐵𝐶) =
𝑚(𝐴𝐵̂ ) + 𝑚(𝐵𝐷)̂
2
9) Ángulo Semiinscrito: es aquel que tiene
como vértice un punto de la
circunferencia, uno de sus lados una
cuerda (o secante) de ella y otro lado una
recta tangente cuyo punto de tangencia
es el vértice del ángulo.
Teorema 4: la medida del ángulo
semiinscrito es igual a la mitad del arco
que interseca, es decir, es igual a la mitad
de la medida del ángulo central
correspondiente.

5. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
𝑚(∡𝐴𝐵𝐶) =
𝑚(𝐵𝐶)̂
2
10) Ángulo Interior: es cualquiera de los
ángulos formados por dos cuerdas que se
intersecan. El punto de intersección es el
vértice del ángulo.
Teorema 5: la medida del ángulo interior
es igual a la semisuma de las medidas de
los arcos determinados por las cuerdas
que forman el ángulo.
𝑚(∡𝐴𝑂𝐶) =
𝑚(𝐴𝐶̂ )+ 𝑚(𝐵𝐷)̂
2
11) Ángulo externo: es aquel ángulo
formado por dos secantes que se
intersecan en un punto fuera de la
circunferencia. El punto fuera de la
circunferencia es el vértice del ángulo.
Teorema 6: La medida del ángulo
exterior es igual a la semidiferencia de
los arcos determinados por las secantes
que lo forman.
𝑚(∡𝐵𝑃𝐶) =
𝑚(𝐴𝐷̂ ) − 𝑚(𝐵𝐶)̂
2
También son ángulos exteriores los
formados por una tangente y una
secante o los formados por dos
tangentes.
𝑚(∡𝑇𝑃𝐵) =
𝑚(𝐴𝑇̂ ) − 𝑚(𝐵𝑇)̂
2
𝑚(∡𝑇𝑃𝐴) =
𝑚(𝑇𝐶𝐴̂ ) − 𝑚(𝐴𝑇)̂
2

6. Facultad de Educación
Pedagogía Básica en Matemáticas
Tópicos de Geometría Euclidiana
Ayudantía 2012
Ejercicios
1) En la figura, 𝐴𝐵̅̅̅̅ es diámetro de la
circunferencia y el arco 𝐶𝐵̂ mide el doble
del arco 𝐴𝐶̂. ¿cuál es la medida del ángulo
ABC?
2) En la figura, la cuerdas 𝐴𝐵̅̅̅̅ y 𝐶𝐷̅̅̅̅ son
perpendiculares y el arco 𝐵𝐷̂ mide 35°.
¿Cuánto mide el arco 𝐴𝐶̂?
3) ¿Cuál es la medida del ángulo α de
acuerdo con los datos de la figura?
4) El triángulo ABC isósceles de base 𝐴𝐵̅̅̅̅ está
inscrito en la circunferencia y el arco 𝐵𝐶̂
mide 100° ¿cuál es la medida del ángulo
β?
5) Si se sabe que α=35° y β=45°, ¿cuál es la
medida del ángulo x de la figura?
6) Los arcos 𝐴𝐶̂ y 𝐷𝐵̂ de la figura miden 108°
y 62°, respectivamente. ¿Cuáles son los
valores de x e y?