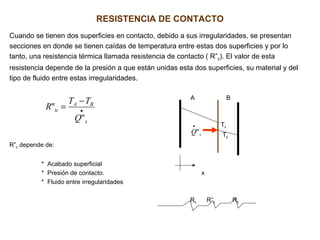
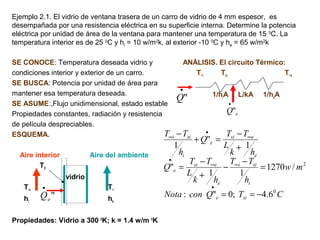
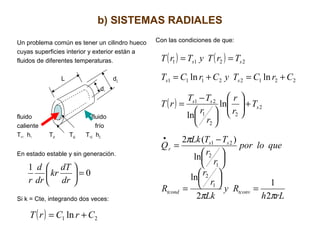
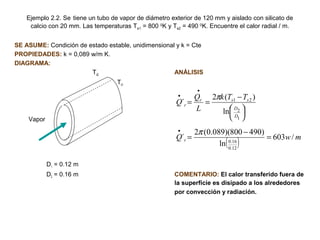
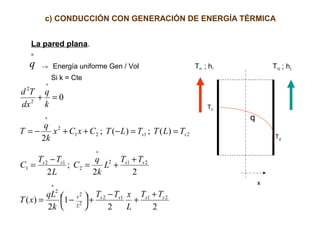
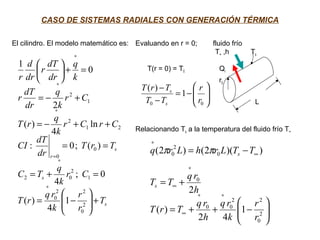
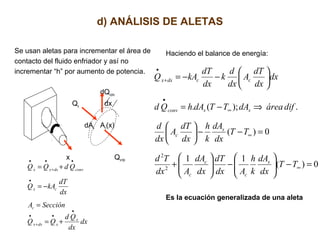
la conducción es una forma de la transferencia de calor siendo esta en estado estable, para asi saber su comportamiento en cada fluido.

1. 2. CONDUCCIÓN
UNIDIMENSIONAL EN ESTADO
ESTABLE.

2. a) LA PARED PLANA
En flujo estable con fuente no distribuida
de energía.
Fluido Fluido
Caliente Ts1 frío
Ts2
T∞1,h1 T∞2,h2
)("
)(
)(
21
21
1
12
12
112
ssx
ssx
s
ss
ss
s
TT
L
k
Q
TT
L
kA
dx
dT
kAQ
Tx
L
TT
xT
entonces
L
TT
CyTC
−=
−=−=
+
−
=
−
==
•
•
21
21
1
)()0(
)(
;,0
ss TLTyTTcony
CxCxT
C
dx
dT
Cteksi
dx
dT
k
dx
d
==
+=∴
===






3. RESISTENCIA TÉRMICA
Haciendo una analogía con el sistema eléctrico:
Re → Resistencia eléctrica; V → Voltaje; I → Intensidad de corriente eléctrica
Rt → Resistencia térmica; T → Temperatura; Q → Calor.
Ah
TT
kA
L
TT
Ah
TT
Q
anteriorcircuitoelEn
hAQ
TT
RconvecciónEn
kA
L
Q
TT
R
A
L
I
VV
R
ssss
x
s
tconv
x
ss
tconde
2
2221
1
11
2121
11
1
:
;
∞∞
•
•
∞
•
−
=
−
=
−
=
=
−
=
=
−
==
−
=
σ

4. CONTINUA RESISTENCIA TÉRMICA
Que representa la resistencia de un circuito de resistencias en serie.
T∞1 Ts1 Ts2 T∞2 T∞1 T∞2
1/h1A L/kA 1/h2A Rtot
AhkA
L
Ah
R
R
TT
Q
TTdeostérEn
tot
tot
x
21
21
21
11
)(
)(min
++=
−
=
−
∞∞
•
∞∞
•
xQ
•
xQ

5. PARED COMPUESTA
Para una pared compuesta.
A B C
Ts1 T2
T3 Ts2
T∞1, h1 T∞4;h4
fluido fluido
caliente x frío
Si; U = Coeficiente global de transferencia de
calor, se define:
•••=
−
=
−
=
++++=∑
∑
−
=
∞
•
∞∞
•
AkL
TT
Ah
TT
Q
AhAk
L
Ak
L
Ak
L
Ah
R
donde
R
TT
Q
AA
ss
x
C
C
B
B
A
A
t
t
x
21
1
11
41
41
1
11
;
UAQ
T
RR
hkLkLkLh
AR
U
x
ttot
CCBBAA
t
1
11
1
1
41
=
∆
==
++++
=
=
•∑
TUAQx ∆=
•

6. CIRCUITO TÉRMICO EN PARALELO
Una pared compuesta como se muestra
A B D
T1 T2
C
El circuito térmico es
RB
RA RD
T1 T2
RC
Se puede representar como:
RA Req RD
Donde.
Y también:
CB
CB
eq
RR
RR
R
+
=
DeqAtot RRRR ++=

7. RESISTENCIA DE CONTACTO
Cuando se tienen dos superficies en contacto, debido a sus irregularidades, se presentan
secciones en donde se tienen caídas de temperatura entre estas dos superficies y por lo
tanto, una resistencia térmica llamada resistencia de contacto ( R”tc). El valor de esta
resistencia depende de la presión a que están unidas esta dos superficies, su material y del
tipo de fluido entre estas irregularidades.
A B
TA
TB
R”tc depende de:
* Acabado superficial
* Presión de contacto. x
* Fluido entre irregularidades
RA R”tc RB
xQ"
•
•
−
=
x
BA
tc
Q
TT
R
"
"

8. Ejemplo 2.1. El vidrio de ventana trasera de un carro de vidrio de 4 mm espesor, es
desempañada por una resistencia eléctrica en su superficie interna. Determine la potencia
eléctrica por unidad de área de la ventana para mantener una temperatura de 15 0
C. La
temperatura interior es de 25 0
C y hi = 10 w/m2
k, al exterior -10 0
C y he = 65 w/m2
k
SE CONOCE: Temperatura deseada vidrio y
condiciones interior y exterior de un carro.
SE BUSCA: Potencia por unidad de área para
mantener esa temperatura deseada.
SE ASUME:,Flujo unidimensional, estado estable
Propiedades constantes, radiación y resistencia
de película despreciables.
ESQUEMA.
Aire interior Aire del ambiente
Td
vidrio
T∞i T∞
hi he
Propiedades: Vidrio a 300 0
K; k = 1.4 w/m 0
K
ANÁLISIS. El circuito Térmico:
T∞i Tsi T∞e
1/hiA L/kA 1/heA
"eQ
•
eQ"
•
•
"Q
CTQconNota
mw
h
TT
hk
L
TT
Q
hk
L
TT
Q
h
TT
sie
i
sii
e
esi
e
e
esi
e
i
sii
0
2
6.4;0":
/1270
11
"
1
"
1
−==
=
−
−
+
−
=
+
−
=+
−
•
∞∞
•
∞
•
∞

9. b) SISTEMAS RADIALES
Un problema común es tener un cilindro hueco
cuyas superficies interior y exterior están a
fluidos de diferentes temperaturas.
L d2
d1
fluido fluido
caliente frío
T∞1 h1 Ts1 Ts2 T∞2 h2
En estado estable y sin generación.
Si k = Cte, integrando dos veces:
Con las condiciones de que:
0
1
=





dr
dT
kr
dr
d
r
( ) 21 ln CrCrT +=
( ) ( )
( )
rLh
Ry
Lk
r
r
R
quelopor
r
r
TTLk
Q
T
r
r
r
r
TT
rT
CrCTyCrCT
TrTyTrT
tconvtcond
ss
r
s
ss
ss
ss
ππ
π
2
1
2
ln
ln
)(2
ln
ln
lnln
1
2
1
2
21
2
2
2
1
21
22122111
2211
=






=






−
=
+











−
=
+=+=
==
•

10. CILINDRO HUECO COMPUESTO (TUBO)
Un tubo con dos capas de otros materiales
T3 Ts4
T2 B C T∞4, h4
r1 A r2 r3
r4
T∞1, h1
Ts1
Considerando el concepto de resistencia
térmica en sistemas radiales, se puede
deducir la ecuación del calor radial como:
Otra forma:
44
3
4
2
3
1
2
11
41
2
1
2
ln
2
ln
2
ln
2
1
LhrLk
r
r
Lk
r
r
Lk
r
r
Lhr
TT
Q
CBA
r
πππππ
+






+






+






+
−
= ∞∞
•
( ) 1
44332211
1
lnlnln
1
1
41
41
:
)(
4
1
13
41
2
31
1
21
1
−
+





+





+





+
∞∞
∞∞
•
∑=
===
=
−=
−
=
t
r
r
hr
r
k
r
r
r
k
r
r
r
k
r
h
tot
r
R
AUAUAUAUquecumpleSe
U
TTUA
R
TT
Q
CBA

11. EL RADIO CRÍTICO
Cuando se usa un aislante en un cilindro o un tubo, se reducen las pérdidas de Calor, se incrementa la
resistencia de conducción. También se tiene el efecto de incrementar el área transferencia de calor por
convección reduciendo la resistencia exterior de la película. Estos efectos se deben cuando al variar el
radio exterior del aislante. Considerando un tubo con una capa de aislante.
T∞1h1 T∞3 , h3
ra
r2 L
Suponiendo que T1 = T2 = T∞t y que h1 y kt son muy grandes
T1 T2T3
r1
r
3
3
2
31
:
2
1
2
ln
∞
∞∞
•
==
+






−
=
h
k
rr
obtieneseceroaigualandoerarespectoderivando
LhrLk
r
r
TT
Q
a
críticoa
a
aa
a
r
ππ
aislanteytubodadesConductivikyk
LhrLk
r
r
Lk
r
r
Lhr
TT
Q
at
aa
a
t
r
3
21
2
11
31
2
1
2
ln
2
ln
2
1
ππππ
+






+






+
−
= ∞∞
•

12. LA ESFERA HUECA
Aplicando este método a una esfera
Hueca, para un volumen de control
Diferencial, la conservación de la energía
requiere que.
r
Ts1 Ts2
dr
En estado estable, unidireccional sin
generación de energía.
Si la Rt se define como la diferencia de
Temperaturas dividida por la razón de calor.
rQ
•
drrQ +
•
drrr QQ +
••
=
CteyrQQcon
dr
dT
rk
dr
dT
kAQ
r
r
)(
)4( 2
••
•
≠
−=−= π






+





−
−
=
=






−=






−





−
=
=−=
∞∞
•
•
•
∫ ∫
hrrrk
TT
Q
hr
R
rrk
R
rr
TTk
Q
CtekdTTk
r
drQ
tconv
tcond
ss
r
r
r
T
T
r
s
s
2
221
12
2
2
21
21
21
2
4
111
4
1
4
1
11
4
1
11
)(4
;)(
4
2
1
2
1
ππ
π
π
π
π

13. Ejemplo 2.2. Se tiene un tubo de vapor de diámetro exterior de 120 mm y aislado con silicato de
calcio con 20 mm. Las temperaturas Ts1 = 800 0
K y Ts2 = 490 0
K. Encuentre el calor radial / m.
SE ASUME: Condición de estado estable, unidimensional y k = Cte
PROPIEDADES: k = 0,089 w/m K.
DIAGRAMA:
Ts2 ANÁLISIS
Ts1
Vapor
D1 = 0.12 m
D2 = 0.16 m COMENTARIO: El calor transferido fuera de
la superficie es disipado a los alrededores
por convección y radiación.
( ) mwQ
TTk
L
Q
Q
r
D
D
ssr
r
/603
ln
)490800)(089.0(2
´
ln
)(2
´
12.0
16.0
1
2
21
=
−
=





−
==
•
•
•
π
π

14. c) CONDUCCIÓN CON GENERACIÓN DE ENERGÍA TÉRMICA
La pared plana.
→ Energía uniforme Gen / Vol T∞1 ; h1 T∞2 ; h2
Si k = Cte
Ts1
q
Ts2
x
∗
q
22
1
2
)(
22
;
2
)(;)(;
2
0
2112
2
2
2
212
2
12
1
2121
2
2
2
ssss
L
x
ssss
ss
TT
L
xTT
k
qL
xT
TT
L
k
q
C
L
TT
C
TLTTLTCxCx
k
q
T
k
q
dx
Td
+
+
−
+



 −=
+
+=
−
=
==−++−=
=+
∗
∗
∗
∗

15. CASO ESPECIAL
Cuando: Ts1 = Ts2 = Ts
-L x L
T∞ h q T∞ h
Qcond Qconv
T0
Ts Ts
Note que en x = 0 no hay transferencia de
Calor a través del plano, puede representarse por una
superficie adiabática. En x = L
Qcond Qconv
T0 q
Ts T∞ h
x L
2
0
0
2
0
2
2
2
)(
2
)0(
1
2
)(






=
−
−
+=≡
+



 −=
∗
∗
L
x
TT
TxT
T
k
qL
TT
T
k
qL
xT
s
s
sL
x
0
0
=
=xdx
dT
h
Lq
TT
L
x
k
qL
dx
dT
xTdoconsideranTTh
dx
dT
k
s
Lx
s
Lx
∗
∞
=
∗
∞
=
+=−=
−=−
;)
2
(
2
)()(
2
2

16. CASO DE SISTEMAS RADIALES CON GENERACIÓN TÉRMICA
El cilindro. El modelo matemático es: Evaluando en r = 0; fluido frío
T∞ ,h Ts
T(r = 0) = T0 Qr
r0
L
Relacionando Ts a la temperatura del fluido frío T∞
s
s
s
r
T
r
r
k
rq
rT
Cr
k
q
TC
TrT
dr
dT
CI
CrCr
k
q
rT
Cr
k
q
dr
dT
r
k
q
dr
dT
r
dr
d
r
+





−=
=+=
==
++−=
+−=
=+





∗
∗
=
∗
∗
∗
2
0
22
0
1
2
02
0
0
21
2
1
2
1
4
)(
0;
4
)(;0:
ln
4
)(
2
0
1






−=
−
−
00
1
)(
r
r
TT
TrT
s
s






−++=
+=
−=
∗∗
∞
∗
∞
∞
∗
2
0
22
00
0
0
2
0
1
42
)(
2
))(2()2(
r
r
k
rq
h
rq
TrT
h
rq
TT
TTLrhLrq
s
sππ

17. Ejemplo 2.3. Se tiene un conductor de cobre calibre 12 (2.33 mm de diámetro). La
resistividad del cobre es de 1.73 x 10-8
Ώm, la conductividad térmica es de 380 w/mK y el
coeficiente de transferencia de calor de 10 10 w/m2
k. Determine la ecuación en función
de la corriente eléctrica de la diferencia de temperaturas máxima y del ambiente.
Para un cilindro la temperatura T( r ) tiene
su valor máximo en el centro, cuando r = 0
Se puede calcular el radio crítico si se forra
el conductor con un material que tenga por
ejemplo una ka = 0.11 w/mK.
Es interesante evaluar ΔT para este caso
del conductor aislado.
( )
( )
( ) ( )
( )
( )
CeniT
xx
xi
T
hr
k
kr
i
TTT
r
i
Lr
Ri
qpero
k
rq
h
rq
TTrT
e
ee
0
2
3232
82
0
2
0
2
max
22
0
2
2
0
2
2
00
max
1079.0
10165.110
3802
1
38010165.14
1073.1
2
1
4
:
42
)0(
=∆






+=∆






+=∆=−
==
++===
−−
−
∞
∗
∗∗
∞
π
π
ρ
π
ρ
π
mm
h
k
R a
crítico 11
10
11.0
===

18. d) ANÁLISIS DE ALETAS
Se usan aletas para incrementar el área de
contacto del fluido enfriador y así no
incrementar “h” por aumento de potencia.
dQconv
Qx dx
dAx Ac(x)
x Qx+dx
Haciendo el balance de energía:
Es la ecuación generalizada de una aleta
dx
dx
Qd
QQ
SecciónA
dx
dT
kAQ
QdQQ
x
xdxx
c
cx
convdxxx
•
•
+
•
•
•
+
••
+=
=
−=
+= 0)(
11
0)(
.);(.
2
2
=−





−





+
=−−





⇒−=






−−=
∞
∞
∞
•
+
•
TT
dx
dA
k
h
Adx
dT
dx
dA
Adx
Td
TT
dx
dA
k
h
dx
dT
A
dx
d
difáreadATTdAhQd
dx
dx
dT
A
dx
d
k
dx
dT
kAQ
s
c
c
c
s
c
ssconv
ccdxx

19. ALETAS DE SECCIÓN UNIFORME
Cuando se tienen aletas como en el
Diagrama Qconv
fluido
T(0) = Tb ; T∞ → fluido T∞ , h
Tb t
Ac = Cte Ac
As = Px Qf w
x
L P = 2w+2t
P → Perímetro Qconv Ac= wt
d
As → área de base a “x” L P = πd
Qf Ac =πd2
/4
Def.
0)(
mod;0
2
2
=−−
=
∞TT
kA
hP
dx
Td
quedaeloel
dx
dA
c
c
:;
)0(
)(
;0
;)()(
21
22
2
tieneSeLxcony
TTCon
CCx
kA
hP
mm
dx
d
dx
dT
dx
d
TxTx
bb
mxmx
c
=
≡−=
+=
≡=−
=−≡
∞
−
∞
θθ
θ
θ
θ
θ
θ


20. CASO (A) Convección en el filo de la aleta
El calor fluye por conducción en la aleta y pasa
a convección en su filo como muestra la figura
Qconv
Tb
Qb = Qf
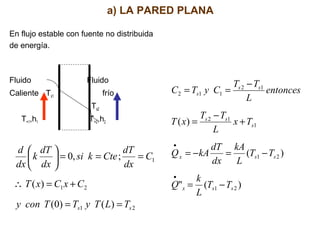
Resolviendo para C1 y C2
Se nota que el gradiente de temperatura
decrece con “x” por la pérdida continua de
calor por convección en caras de la aleta.
Af → Área total de aleta incluyendo el filo
de la aleta.
])([ ∞
=
−→− TLThA
dx
dT
kA c
Lx
c
)()(
)(
])([
2121
21
mLmLmLmL
b
Lx
Lx
cc
CCkmCCh
CC
dx
dT
kLh
dx
dT
kATLThA
−−
=
=
∞
−=+
+=
−=
−=−

θ
θ
mLSenh
mk
h
mLCosh
xLmSenh
mk
h
xLmCosh
b
..
)(.)(.






+
−





+−
=
θ
θ
[ ] s
AA
sf
bcf
x
c
x
cfb
dAxhdATxThQ
mLSenh
mk
h
mLCosh
mLCosh
mk
h
mLSenh
hPkAQ
dx
d
kA
dx
dT
kAQQ
ff
∫∫ =−=






+






+
=
−=−==
∞
•
•
==
••
)()(
..
..
00
θ
θ
θ

21. OTROS CASOS DEL ANÁLISIS DE LA ALETA
CASO (B). Si la convección en el filo del aleta
es despreciable, se trata como adiabático.
NOTA. Para usar los resultados del análisis
del CASO (A), se tiene que en la práctica es
válido si (mL) < 2.65. Si (mL) ≥ 2.65 se puede
usar la aproximación infinita.
CASO ( C). Θ(L) = θL
CASO ( D ). L → ∞ ; θL → omLTanhhPkAQ
mxCosh
xLmCosh
dx
d
bcf
b
Lx
.
.
)(.
0
θ
θ
θ
θ
=
−
=
=
•
=
( )
( )
mLSenh
mLCosh
hPkAQ
mLSenh
xLSenhmxSenh
bL
bcf
bL
b
.
.
.
)(.
θθ
θ
θθ
θ
θ
−
=
−+
=
•
bcf
mx
b
hPkAQ θ
θ
θ
=
=
•
−


22. EJEMPLO 2.4. Una barra de bronce de 0.1 m largo y 0.005 m diámetro, se extiende
horizontalmente de una fundición a Tb = 200 0
C.La barra está en el ambiente a T∞ = 200
C
y h = 30 w/m2
K. ¿ cual es la temperatura de la barra a 0.025, 0.050 y 0.1 m ?. Bronce a
110 0
C; k = 133 w/mK
Diagrama. L = 0.1 m
Aire a T∞ y h x1 = 0.025 m,
x2 = 0.050 m
Tb d
x1 x2 L
x :
Evaluando.
b
c
mLSeh
mk
h
mLCosh
xLmSenh
mk
h
xLmCosh
mLconm
x
x
kd
h
d
k
dh
kA
hP
m
θθ
π
π
..
)(.)(.
34.143.13
005.0133
304
4
4
1
21
21
21
2
21






+
−





+−
=
==





=






=


















=





=
−
)180(
07.2
)(.0168.0)(.
18020200:
0168.0
005.0133
30
78.1.;04.2.
xLmSehxLmCosh
cony
xmk
h
mLSenhmLCosh
b
−+−
=
=−=
=





=





≈≈
θ
θ
X(
m)
Cosh.
m(L-x)
Senh.
m(L-x)
θ T(0
)
X1 1.55 1.19 136.5 156.5
X2 1.24 0.725 108.9 128.9
L 1.00 0.00 87.0 107.0

23. RENDIMIENTO DE ALETAS
Rendimiento de una aleta
εf → Efectividad. Relación de la transferencia
de calor de la aleta a la razón de calor
transferido si no existiera la aleta. εf > 2 para
justificar las aletas.
En caso ( D )
El rendimiento se puede evaluar en términos
de resistencia térmica.
Acb → Área de sección transversal de aleta
en su base.
Eficiencia de una aleta “ηf”.
Af → Área de la superficie de la aleta.
Aleta recta, área transversal uniforma y filo
adiabático.
Filo adiabático, sección recta o cilíndrica
2
1






=
c
f
hA
kP
ε
tconv
tcond
f
cb
tconv
f
b
tcond
R
R
hA
Ry
Q
R
=
== •
ε
θ 1
ff
ff
f
hA
Q
Q
Q
θ
η
•
•
•
=≡
max
∞→≤≤== L
mL
mLTanh
hPL
mLMTanh
f
b
f ;10;
..
η
θ
η
c
c
f
bccf
c
c
mL
mLTanh
hPkAMmLMTanhQ
cilíndricaSecc
d
LL
rectaSecc
t
LL
.
.;.
4
2
=
==
→+=
→+=
•
η
θ

24. RENDIMIENTO DE ALETAS II
Errores con la aproximación despreciables si: Aleta sección transversal no-uniforme:
Caso de secc. anular; Ac = 2πrt, varía con “r ”
Reemplazando “r” por “x” en Ec. de calor.
2
3
2
1
2
1
2
1
2
1
2
2
2
0625.0
2
c
p
c
cp
c
c
cc
c
c
L
kA
h
mL
tLAcony
L
L
porndomultiplica
L
kt
h
L
kA
hP
mL
ywPtwSi
k
hd
ó
k
ht








=
=














=





=
≈⇒>>
≤
( )
clasesegundayprimera
ceroordenBesseldefuncionesKyI
mrKCmrICrsolución
m
dr
d
rdr
d
TTy
kt
mcon
SupladeÁrearrA
TT
kt
h
dr
dT
rdr
Td
s
00
0201
2
2
2
2
2
1
2
2
2
)()()(:
0
1
2
2
0)(
21
+=
=−+
−=≡
→−=
=−−+
∞
∞
θ
θ
θθ
θ
π
π

25. RENDIMIENTO DE ALETAS III
Eficiencia secc transversal no uniforme
t
r2c = r2 + t/2
r1 L Lc = L + t/2
Ap = Lct
r2
aletadetérmicasistencia
hA
R
mrKmrImrImrK
mrKmrImrImrK
rrm
r
rrh
Q
mrKmrImrImrK
mrKmrImrImrK
mtkr
dr
d
trk
dr
dT
kAQ
mrImrKmrKmrI
mrImrKmrKmrI
ff
taleta
b
f
f
b
rrrr
cbf
b
Re
1
)()()()(
)()()()(
)(
2
)(2
)()()()(
)()()()(
)2(
)2(
)()()()(
)()()()(
21102110
21112111
2
1
2
2
1
2
1
2
2
21102110
21112111
1
1
21102110
210210
11
→=
+
−
−
=
−
=
+
−
=
−=−=
+
+
=
•
==
•
η
θπ
η
θπ
θ
π
θ
θ

26. EFICIENCIA DE SUPERFICIE GLOBAL
Se tienen “N” aletas en un equipo térmico, la eficiencia de superficie global es:
)1(1
exp
max
f
T
f
o
bbbffT
T
bfT
f
bf
ff
o
A
NA
hAhANQ
ÁreaTotalA
aletasdeNúmeroN
ANAA
uestaporciónÁreaaletadeÁreaA
hA
Q
Q
Q
ηη
θθη
θ
η
−−=
+=
→
→
+=
+→
==
•
•
•
•

27. Problema: Vapor de agua fluye por tubo Dext = D1 = 3 Cm a T = 120 0
C. El tubo tiene aletas
circulares de Al (k = 180 w/m 0
C) de D2 = 6 Cm y espesor, t = 2 mm. El espacio entre aletas
es de 3 mm por lo que son 200 aletas/m. El aire exterior está a T∞ = 25 0
C, h = 60 W/m2
K.
Determine el incremento de la TC del tubo/m por la adición de las aletas.
Análisis:
Si no se tienen aletas:
Asa = πD1L = π (0.03)(1) = 0.0942 m2
Para aletas circulares sujetas a un tubo en
una gráfica se tiene:
Con estos datos en la gráfica de eficiencia para esta aleta:
η = 0.96
La TC en parte libre de aletas es:
W
TThAQ bsasa
537
)25120)(0942.0(60)(
=
−=−= ∞
•
07.2
)102.3(80
60
)016.0(
07.2
015.0
031.0
102.3)002.0(016.0
016.0015.0
031.003.0
015.)03.006.0()(
5
2
33
2
2
25
2
002.0
2
2
002.0
222
2
1
122
1
2
===
==
===
=+=+=
=+=+=
==−=−=
−
−
xkA
h
L
r
r
mxtLA
mLL
mrr
mDDL
p
c
cp
t
c
t
c
c
ξ
W
TThAQQ
mrrA
baletaaletaaletaaleta
caleta
3.25)25120)(004624.0)(60(96.0
)(
004624.0)015.0031.0(2)(2
max
2222
1
2
2
=−=
−==
=−=−=
∞
••
ηη
ππ
10
537
5380
48435375380
5380)6.13.25(200)(200
/200
6.1
)25120)(000283.0(60)(
000283.0)003.0)(03.0( 2
1
≈==
=−=−=
=+=+=
∴
=
−=−=
===
•
•
•••
•••
∞
•
sa
T
aleta
saTincremento
librealetaT
blibrelibre
libre
Q
Q
WQQQ
WQQQ
maletastienenSe
W
TThAQ
mSDA
ε
ππ