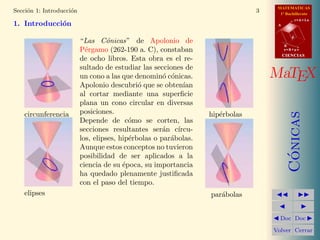
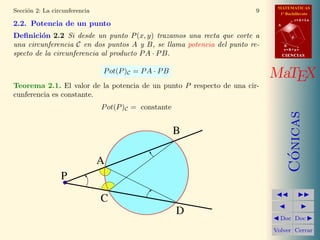
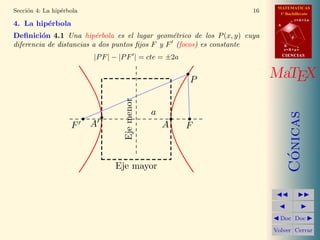
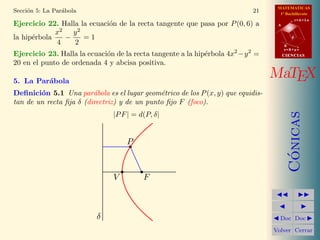
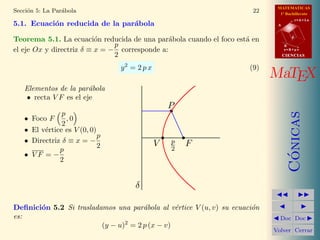
Este documento presenta información sobre las cónicas. Explica que las cónicas son las secciones cónicas de un cono y pueden ser círculos, elipses, hipérbolas o parábolas. Describe las ecuaciones reducidas de la circunferencia, elipse, hipérbola y parábola. También cubre conceptos como el centro, radio, vértices y focos de estas curvas.


















![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Secci´on 6: Expresi´on general de las c´onicas 24
6. Expresi´on general de las c´onicas
Empezaremos con un ejemplo. Considera la ecuaci´on de segundo grado
con dos inc´ognitas x e y siguiente:
2 x2
+ 3 y2
− 4 x − 12 y + 8 = 0
Para conseguir la ecuaci´on reducida de la c´onica se agrupan cuadrados de la
siguiente forma
2 x2
− 4 x = 2(x2
− 2x) = 2(x2
− 2x + 1 − 1) = 2[(x − 1)2
− 1]
3 y2
− 12 y = 3(y2
− 4y) = 3(y2
− 4y + 4 − 4) = 3[(y − 2)2
− 4]
sustituyendo en la expresi´on dada se obtiene
2[(x − 1)2
− 1] + 3[(y − 2)2
− 4] + 8 = 0
operando
2(x − 1)2
+ 3(y − 2)2
= 6
dividiendo por 6, se obtiene la ecuaci´on reducida de la elipse
(x − 1)2
3
+
(y − 2)2
2
= 1
Definici´on 6.1 La ecuaci´on general de segundo grado en x e y
A x2
+ B y2
+ C x + D y + E = 0 (11)
corresponde a una de las c´onicas: circunferencia, elipse, hip´erbola o par´abola.
Para llegar a su ecuaci´on reducida se agrupan cuadrados.](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-24-320.jpg)

















![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Prueba de los Teoremas 43
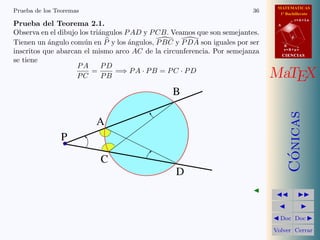
Prueba del Teorema 3.2.
Hallamos la derivada de
x2
a2
+
y2
b2
= 1
en el punto P(x0, y0)
2 x
a2
+
2 y y
b2
= 0 =⇒ y = −
b2
a2
·
x0
y0
y − y0 = m (x − x0) [m = y (x0)]
y − y0 = −
b2
a2
·
x0
y0
(x − x0) [operando]
b2
x0 x + a2
y0 y = b2
x2
0 + a2
y2
0 [b2
x2
0 + a2
y2
0 = 1]
ecuaci´on de la tangente
x0 x
a2
+
y0 y
b2
= 1](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-43-320.jpg)







![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Prueba de los Teoremas 51
Prueba del Teorema 4.2.
Hallamos la derivada de
x2
a2
−
y2
b2
= 1
en el punto P(x0, y0)
2 x
a2
−
2 y y
b2
= 0 =⇒ y =
b2
a2
·
x0
y0
y − y0 = m (x − x0) [m = y (x0)]
y − y0 =
b2
a2
·
x0
y0
(x − x0) [operando]
b2
x0 x − a2
y0 y = b2
x2
0 − a2
y2
0 [b2
x2
0 − a2
y2
0 = 1]
ecuaci´on de la tangente
x0 x
a2
−
y0 y
b2
= 1](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-51-320.jpg)







![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Prueba de los Teoremas 59
Prueba del Teorema 5.2.
Hallamos la derivada de y2
= 2 p x en el punto P(x0, y0)
2 y y = 2 p =⇒ y =
p
y0
y − y0 = m (x − x0) [m = y (x0)]
y − y0 =
p
y0
(x − x0) [operando]
y y0 − y2
0 = p (x − x0) [y2
0 = 2 p x0]
y y0 = p x + p x0
ecuaci´on de la tangente
y y0 = p x + p x0](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-59-320.jpg)

![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Soluciones a los Ejercicios 61
Ejercicio 29(a) Para conseguir la ecuaci´on reducida de la c´onica
9 x2
+ 16 y2
− 36x + 96y + 36 = 0
se agrupan cuadrados de la siguiente forma
9 x2
− 36 x = 9(x2
− 4x) = 9(x2
− 4x + 4 − 4) = 9[(x − 2)2
− 4]
16 y2
+ 96 y = 16(y2
+ 6y) = 16(y2
+ 6y + 9 − 9) = 16[(y + 3)2
− 9]
sustituyendo y operando en la expresi´on dada se obtiene
9(x − 2)2
+ 16(y + 3)2
= 144
dividiendo por 144, se obtiene la ecuaci´on reducida de la elipse
(x − 2)2
16
+
(y + 3)2
9
= 1
0(2, −3) a = 4 b = 3 c =
√
7 e =
√
7
4](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-61-320.jpg)

![MATEMATICAS
1º Bachillerato
A
s = B + m v
r = A + l u
B
d
CIENCIASCIENCIAS
MaTEX
C´onicas
Doc Doc
Volver Cerrar
Soluciones a los Ejercicios 63
Ejercicio 29(c) Para conseguir la ecuaci´on reducida de la c´onica
x2
+ 9 y2
− 36 y + 27 = 0
se agrupan cuadrados de la siguiente forma
9 y2
− 36 y = 9(y2
− 4y) = 9(y2
− 4y + 4 − 4) = 9[(y − 2)2
− 4]
sustituyendo y operando en la expresi´on dada se obtiene
x2
+ 9(y − 2)2
= 9
dividiendo por 9, se obtiene la ecuaci´on reducida de la elipse
x2
9
+
(y − 2)2
1
= 1
0(0, 2) a = 3 b = 1 c =
√
8 e =
√
8
3](https://image.slidesharecdn.com/conicas-180904220436/85/Conicas-63-320.jpg)
