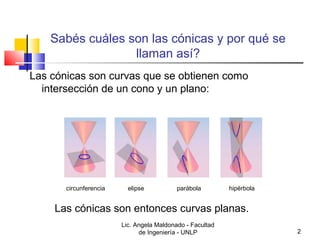
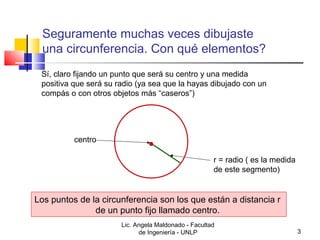
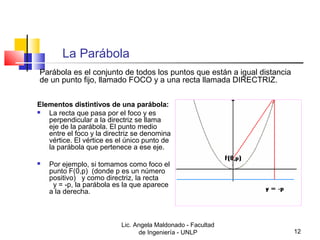
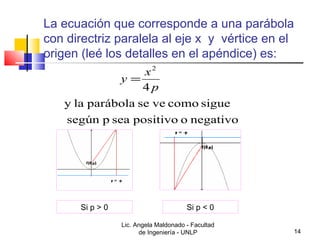
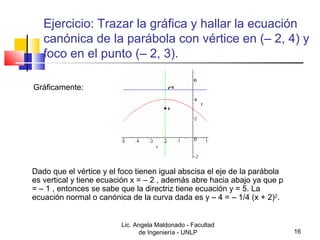
1) El documento trata sobre las cónicas, curvas planas obtenidas al cortar un cono circular recto con un plano. Describe cómo trazar circunferencias, parábolas, elipses e hipérbolas. 2) Explica cómo encontrar la ecuación de una circunferencia dados su centro y radio, y cómo determinar si un punto pertenece a una circunferencia. 3) Detalla los elementos que definen una parábola (foco, directriz, vértice) y cómo graficar una, así como también cómo encontrar su ecu

1. 1
Lectura de Cónicas

2. Sabés cuáles son las cónicas y por qué se
llaman así?
Las cónicas son curvas que se obtienen como
intersección de un cono y un plano:
circunferencia elipse parábola hipérbola
Las cónicas son entonces curvas planas.
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 2

3. Seguramente muchas veces dibujaste
una circunferencia. Con qué elementos?
Sí, claro fijando un punto que será su centro y una medida
positiva que será su radio (ya sea que la hayas dibujado con un
compás o con otros objetos más “caseros”)
r = radio ( es la medida
de este segmento)
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 3
centro
Los puntos de la circunferencia son los que están a distancia r
de un punto fijo llamado centro.

4. El punto (4,6) está en la circunferencia
de centro (3,5) y radio 1,4?
Qué te parece?, cómo harías para poder responder a esta
pregunta? ¿alcanza con que dibujes con un compás la
circunferencia?, si no lo hiciste, hacelo…el punto (4,6) está en la
circunferencia?, que respondiste?, que sí?............
¿te quedan dudas?, ¿cómo podrías hacer para resolver esta
situación y que no queden dudas?
¡¡Este es un gran momento!!:
graficar una situación no siempre resuelve las situaciones
que se nos plantean, por ello, como en este caso, es
necesario trabajar con la definición de circunferencia para
obtener una herramienta que permita resolver esta
situación
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 4

5. Cómo se establece una condición que satisfacen
todos los puntos de esa circunferencia y sólo
ellos?
La circunferencia de centro (3,5) y radio 1,4 es el conjunto de todos los
puntos del plano que están a distancia 1,4 del punto (3,5). Así que
podemos decir, sin lugar a dudas que:
El punto (x,y) es un punto de la circunferencia mencionada si y sólo si:
Distancia((x,y), (3,5)) = 1,4
Y por la definición de distancia entre dos puntos, esta ecuación es
equivalente a las siguientes:
(x - 3)2 + ( y - 5)2 =1,4
(x - 3)2 + ( y - 5)2 = (1,4)2
(x -3)2 +( y -5)2 =1,96
Esta es la ecuación de
la circunferencia de
centro (3,5) y radio 1,4
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 5

6. Así, ahora es fácil resolver nuestro problema (el
punto (4,6) está en la circunferencia de centro
(3,5) y radio 1,4?)
Cómo?, verificando si las coordenadas del punto (4,6) satisfacen la
ecuación que obtuvimos:
(4 - 3)2 + (6 - 5)2 =1,96
Pero está claro que esta ecuación no se satisface, ya que el miembro
de la izquierda es 2.
Podemos ahora responder sin dudas que el punto (4,6) no es un punto
de la circunferencia dada.
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 6

7. Así, la ecuación de la circunferencia con centro
en el punto (a,b) y de radio r es:
(x - a)2 + (y - b)2 = r2
Esta es la ecuación
estándar de la
circunferencia con
centro (a,b) y radio r
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 7

8. Si te doy las siguientes ecuaciones cuadráticas
en x e y, podrías decirme en cada caso si se
trata de la ecuación de una circunferencia?
a) x2 + y2 - 2x + 3y = 0
b) x2 + y2 - 2x + 3y = -4
c) x2 + 1 y2 - x + y =
2 3 0
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 8
2

9. Voy a hacer los dos primeros casos y el último
te lo dejo a vos (podés consultar con tu tutor)
a) x2 + y2 - 2x + 3y = 0
Completando cuadrados, se ve con claridad que la ecuación dada es
equivalente a las siguientes:
2
÷ø
2 ( 1) 3 3 3
÷ø
= 0 + ( - 1) + æ x - x + - + y + y + æ
1 9
( x - 1) + æ y +
3
ö çè
13
( x - 1) + æ y +
3
ö çè
Lic. Angela Maldonado - Facultad
2
2
de Ingeniería - UNLP 9
2 2 2
2
2
ö çè
ö çè
4
2
2
2 + = ÷ø
4
2
2
2 = ÷ø
Y esta es claramente la ecuación estándar de la circunferencia con centro
(1, -3/2) y radio
13
2

10. b) x2 + y2 - 2x + 3y = -4
Completando cuadrados, se ve con claridad que la ecuación dada es
equivalente a las siguientes:
2
÷ø
2 ( 1) 3 3 3
÷ø
= - 4 + ( - 1) + æ x - x + - + y + y + æ
4 1 9
( x - 1) + æ y +
3
ö çè
3
( x - 1) + æ y +
3
ö çè
Lic. Angela Maldonado - Facultad
2
2
de Ingeniería - UNLP 10
2 2 2
2
2
ö çè
ö çè
4
2
2
2 + + - = ÷ø
4
2
2
2 - = ÷ø
Y es claro que esta ecuación NO CORRESPONDE a una circunferencia!!
¿¿podés expresar con claridad por qué???

11. Hasta aquí, tenés que tener en claro
que la circunferencia:
 Es una curva plana que se obtienen al cortar un cono circular recto con
un plano (perpendicular al eje del cono) y tiene propiedades
geométricas que la definen y permiten su trazado con elementos
comunes (Un clavo un piolín y un lápiz, un compás, etc..)
 Todos y sólo los puntos de una circunferencia, pueden caracterizarse a
través de ecuaciones cuadráticas en x e y. La ecuación estándar de
una circunferencia muestra con claridad cuál es el centro y el radio de
la misma.
 Las ecuaciones de las cónicas son útiles para reconocerlas, resolver
situaciones de pertenencia, intersecciones con otras curvas, etc.
 La completación de cuadrados y el reconocimiento de la ecuación
estándar de una circunferencias son fundamentales a la hora de decidir
si una ecuación cuadrática en x e y es la ecuación de una
circunferencia.
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 11

12. Parábola es el conjunto de todos los puntos que están a igual distancia
de un punto fijo, llamado FOCO y a una recta llamada DIRECTRIZ.
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 12
La Parábola
Elementos distintivos de una parábola:
 La recta que pasa por el foco y es
perpendicular a la directriz se llama
eje de la parábola. El punto medio
entre el foco y la directriz se denomina
vértice. El vértice es el único punto de
la parábola que pertenece a ese eje.
 Por ejemplo, si tomamos como foco el
punto F(0,p) (donde p es un número
positivo) y como directriz, la recta
y = -p, la parábola es la que aparece
a la derecha.

13. No es tan conocido cómo graficar una
parábola, por eso ahí va la receta:
Para trazar una parábola necesitás:
 una regla,
 una escuadra,
 un lápiz,
 un piolín que tenga la medida exacta
de un cateto de la escuadra. El piolín
se sujeta al extremo del cateto que
corresponde al ángulo agudo y
 Un clavo o tachuela, que se clavará
en el “foco” de la parábola y que
sujetará el otro extremo del piolín.
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 13
Mirá la figura e intentálo!!!!

14. La ecuación que corresponde a una parábola
con directriz paralela al eje x y vértice en el
origen (leé los detalles en el apéndice) es:
y = x
4
2
p
y la parábola se ve como sigue
según p sea positivo o negativo
Si p > 0 Si p < 0
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 14

15. También podés ver en detalles que:
La ecuación que corresponde a una parábola con directriz
paralela al eje x y vértice en el punto (a,b) es:
( )
4
2
p
y - b = x - a
La ecuación que corresponde a una parábola con directriz
paralela al eje y y vértice en el punto (a,b) es:
( )
4
2
p
x - a = y -b
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 15

16. Ejercicio: Trazar la gráfica y hallar la ecuación
canónica de la parábola con vértice en (– 2, 4) y
foco en el punto (– 2, 3).
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 16
Gráficamente:
Dado que el vértice y el foco tienen igual abscisa el eje de la parábola
es vertical y tiene ecuación x = – 2 , además abre hacia abajo ya que p
= – 1 , entonces se sabe que la directriz tiene ecuación y = 5. La
ecuación normal o canónica de la curva dada es y – 4 = – 1/4 (x + 2)2.

17. La elipse, cómo puedo trazar una?
 Una elipse es el conjunto de los puntos del plano tales que la suma
de sus distancias a dos puntos fijos F’ y F, llamados focos, es
constante.
 El punto medio del segmento que une los focos se denomina centro.
 Para visualizar la definición de la elipse, basta imaginar dos chinches
clavados en los focos y un trozo de cuerda atada a ellos. Al ir
moviendo un lápiz que tensa esa cuerda, su trazo irá dibujando una
elipse, como se muestra en la siguiente figura:
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 17

18. La ecuación de la elipse con centro en el
origen:
La ecuación estándar de una elipse con centro en el origen y focos F
y F´ en el eje x como se muestra en la figura, es:
2
2
+ = =
Notá que a y b son las longitudes de los semiejes mayor y menor
respectivamente
2
+ =
x
Lic. Angela Maldonado - Facultad
2
y
de Ingeniería - UNLP 18
x
Gráficamente:
1, donde b2 a2 - c2
2
2
y
b
a
Si los focos están sobre el eje y, la ecuación es 1 y es claro
que el eje mayor estará sobre el eje y 2
2
a
b

19. La ecuación de la elipse con centro en el punto
(x0, y0):
 Si los focos están sobre una recta paralela al eje X
(x - x ) + ( - ) =1 , >
a b
y y
b
 Si los focos están sobre una recta paralela al eje y
(x - x ) + ( y - y
) = 1 , >
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 19
a
2
2
0
2
2
0
a b
a
b
2
2
0
2
2
0

20. Ejercicio: hallar una ecuación de la elipse de la
figura y determinar si el punto (- 5/2,2) está en
dicha elipse?
Está claro en el dibujo que:
 El centro de la elipse es el punto (-2,4)
 Los semiejes mayor y menor miden 3 y 1
( 4)
( 2)
2 2 2 2
- + + - = - + ( - 2)
= + ¹
9
( 1/ 2)
1
(2 4)
9
Lic. Angela Maldonado - Facultad
1
4
9
1
4
de Ingeniería - UNLP 20
respectivamente
 El eje mayor es paralelo al eje y
Entonces, la ecuación es:
1
( 4)
3
( ( 2))
1
2
2
2
2
x - - + y - = ó
1
9
1
2 2
x + + y - =
Ahora queda sólo verificar si el punto (-5/2,2) satisface la ecuación:
(( 5 / 2) 2)
1
Por lo que se concluye que (- 5/2,2) no es un punto de la elipse.

21. 2
- =
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 21
La Hipérbola
 Hipérbola es el conjunto de puntos del
plano para los que que el valor
absoluto de la diferencia de sus
distancias a dos puntos fijos F’ y F,
llamados focos, es constante. El punto
medio del segmento que une los focos
se denomina centro.
 La Ecuación de la hipérbola de la
figura (con centro en el origen y focos
sobre el eje x), es:
2
1 2
2
y
b
x
a
Notar que a y –a son las absisas de los puntos de la hipérbola sobre el eje x,
que c es la distancia de los focos al centro y que b2 = c2 - a2.

22. La ecuación de la hipérbola con centro en el
punto (x0, y0) es:
La ecuación de una hipérbola con centro en (x0, y0) y focos en el eje y = y0
2
y y
x x
( ) ( ) 1
2
0
x x
y y
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 22
2
2
- 0 - - =
b
a
Notar que x0+a y x0–a son las absisas de los puntos de la hipérbola sobre
el eje y = y0 , c es la distancia de los focos al centro y b2 = c2 - a2.
La ecuación de una hipérbola con centro en (x0, y0) y focos en el eje x = x0
( ) ( ) 1
2
2
0
2
2
- 0 - - =
b
a
Notar que y0+a e y0–a son las ordenadas de los puntos de la hipérbola
sobre el eje x = x0 , c es la distancia de los focos al centro y b2 = c2 - a2.

23. Ejercicio: hallar una ecuación de la hipérbola de
la figura y determinar si el punto (2,2) está en
dicha hipérbola?
Está claro en el dibujo que:
 El centro de la hipérbola es el punto (4,0)
 Los focos están en el eje X = 4
 a = 1, c = 2, b2 = 22-12 = 3
Entonces, la ecuación es:
1
( 0) ( 4)
2
1
- - - = - ¹
4 4
3
(2 0) (2 4)
2
3
Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 23
3
2
1
2
y - - x - =
Ahora queda sólo verificar si el punto (2,2) satisface la ecuación:
2
1
2
Por lo que se concluye que (2,2) no es un punto de la hipérbola dada.

24. Lic. Angela Maldonado - Facultad
de Ingeniería - UNLP 24
Conclusiones:
 Las cónicas son curvas planas que se obtienen al cortar un cono
circular recto con planos.
 Tienen propiedades geométricas que las definen y permiten su
trazado con elementos comunes (clavos, piolines,…)
 Todos y sólo los puntos de cada una de estas curvas, pueden
caracterizarse a través de ecuaciones.
 Las ecuaciones de las cónicas son útiles para reconocerlas, resolver
situaciones de pertenencia, intersecciones con otras curvas, etc.