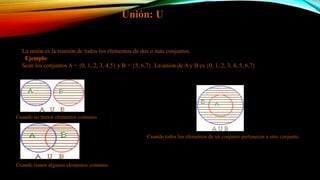
Este documento define y explica conceptos básicos de teoría de conjuntos, incluyendo unión, intersección, diferencia, complemento y diferencia simétrica. La unión combina los elementos de dos o más conjuntos en un solo conjunto. La intersección incluye solo los elementos comunes a dos conjuntos. La diferencia incluye los elementos de un conjunto que no pertenecen al otro. El complemento incluye los elementos fuera de un conjunto dentro de un universo dado. La diferencia simétrica incluye los elementos que no son comunes a dos conjuntos. Cada

1. REPUBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
EXTENSIÓN BARCELONA
BARCELONA- EDO. ANZOÁTEGUI
Profesor: Bachiller:
Asdrúbal Rodríguez Domínguez Argimiro
C.I:25245074
Bna,12/03/16

2. La unión es la reunión de todos los elementos de dos o más conjuntos.
Ejemplo:
Sean los conjuntos A = {0, 1, 2, 3, 4,5} y B = {5, 6,7}. La unión de A y B es {0, 1, 2, 3, 4, 5, 6,7}
Cuando no tienen elementos comunes
Cuando tienen algunos elementos comunes
Cuando todos los elementos de un conjunto pertenecen a otro conjunto
Unión: U

3. Se define como la aparición de un tercer conjunto compuesto por los elementos en común de los conjuntos de donde
proviene, sean dos conjuntos A y B.
Ejemplo:
1.Sea A definido así: A = {j, u, g, o, d, e}
2.Sea B definido así: B = {m, a, n, g, o}
3.La INTERSECCIÓN se representa así AÇB = {g, o}
Intersección: Ç

4. Se denomina diferencia de dos conjuntos A y B al conjunto formado por todos los elementos de A pero que no
pertenecen a B. La diferencia se denota por: A - B que se lee: A diferencia B o A menos B.
Ejemplo:
A ={1;2;3;4;5;6;7}yB={5;6;7;8;9}
A-B={1;2;3;4}
A-B={x/x ∈ A ^ x € B}
Diferencia: A-B-B
Cuando no tienen elementos comunes
Cuando todos los elementos de un conjunto
pertenecen al otro conjunto

5. Complemento: A∁
Son aquellos números que no se encuentran en el conjunto pero que existen en el Universo
Si el conjunto dado A = {1, 2, 3} y el conjunto universal U contiene todos los números naturales menores a
6, entonces el complemento del conjunto dado A = {4, 5}.
Ejemplo:
Si el conjunto universal es U = { a, b, c, d, e } y A = { b, c, d }, entonces el complementario de A respecto
de U está formado por los elementos del universal que no estén en A, esto es:
Al = { a, e }
Los conjuntos { a, e } y { b, c, d } son complementarios.
U={1;2;3;4;5} y A={1;2;5}
A’={3;4}
Los conjuntos {3;4} y {1;2;5} son complementarios

6. DIFERENCIA SIMÉTRICA: AΔ B
Es el conjunto formado por la parte no común de los conjuntos.
Ejemplo: A= {2;4;6;8;10} B= {2;4;5;7;9} AΔ B = (AUB) –(A∩B)
Ejemplo 2: A= {1;2;3;4;5;6;7} y B= {5;6;7;8;9}