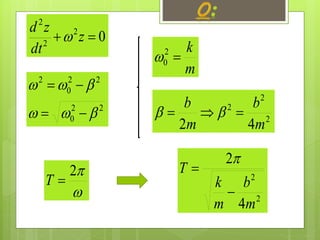
El documento presenta la resolución de una ecuación diferencial de segundo orden que describe el movimiento armónico simple de un oscilador. Se identifican tres casos posibles dependiendo de la relación entre los parámetros k y β del oscilador. Se obtienen expresiones analíticas para la solución en cada caso.

1. • Físico: Galarza Espinoza.
• moisesperu15@gmail.com

3. F  ky
F bv b  

4. ma   ky 
bv

F  ma
0
0
d y
d y
d y
2
2
2
2
2
2
  
dy
b
dy
  
y
k
dy
b
  
m
dt
m
dt
ky
dt
dt
m
dt
ky b
dt
m

5. 
 ma F
0
k
dy
b
b
  
2
y
dy
2 0
d y
d y
2 0
2
2
2
  
dt
dt
y
m
dt
m
dt
 
2 
m

6. • Haciendo un cambio de variable:
y z e t  
dy dz
   
   d y dz
d z
dz
              2
  t t t t e z e
dt
dt
e
dt
e
dt
2
2
2
2
t t z e
dt
e
dt

7. • Reemplazando en:
dy
2 0 2
d x
2 0
 2 2  0
d z
2 0
2
  z 
dt
 
2
  y 
dt
dt
 
• Tenemos:
2   
2 2
0
0 2
d z
2
2
 z 
dt


8. • Es un M.A.S:
0 2
d z
2
2
 z 
dt

  
• Analicemos : 2
• Analicemos cuando:
2 2
0
 
2 2
0
2
   

   

caso a
2 2
0
2 2
1 0
:
 

:

0
caso b

2 2
0
 

2 2
0
:
   

caso c
2 2
0
 

i

9. 2 2
0 • Caso a:       
0 z  ACos  t   2
d z
2
2
 z 
dt

• Recordando:
t y z e  
• Nuestra solución será:
       y Ae Cos t t
2 2
1 0

10. 0 2
d z
2
2
 z 
dt

2 2
0
   

2 2
0
2
   

2

T 
k
 2
0 
m
2
2
2
b
b
   
m
2 4m
2
2
b
4
2
m
k
m
T




11.        y Ae Cos t t
t Amplitud Ae  

12. 0 2
d z
2
2
 z 
dt

0 2 2
0     
• La ecuación se reduce a:
t y z e  
• Caso b:
d z
0 2
2

dt

13. • Operando:
z d
0 2
2

dt
z  ct  B
t y ze  
  t y B ct e   
• Recordando:
• La solución :

14. y ze t  
  t y B ct e   

15. 2 2
0
• Caso c:
      i 1
0 2
d z
2
2
 z 
dt
• La ecuación se reduce a:
0 2
d z
2
2
 z 
dt


16. • Operando:
d z
2
2
 z 
dt

z e t  
t y ze  
0 2
• Probando con:
t z e  
• La combinación también cumplirá:
t t z e e    
• Solución general:
t t z Be Ce    

17. • De la solución general:
t t z Be Ce    
• recordando:
y ze t  
• Solución buscada:
t  t t  y e Be Ce     

18. t  t t  y e Be Ce     