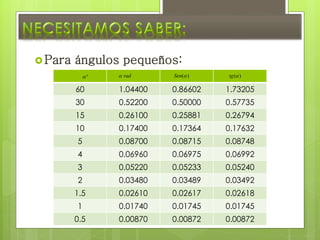
Este documento presenta varios problemas relacionados con la mecánica de materiales y la deformación de cuerpos elásticos. Incluye conceptos como la ley de Hooke, equilibrio de fuerzas, ángulos pequeños y problemas específicos sobre alambres, vigas, tensores y columnas sometidas a cargas y fuerzas.

1. • Físico: Galarza Espinoza.
• moisesperu15@gmail.com

5.  Ley de Hooke.
 Esfuerzo y Deformación Unitaria.
 
m
N
k
F
k
kF






0
0
0 


 






A
F

6. ndeformacio
esfuerzo
elasticomodulo


 A
F
Y



7.  1ra Condición de Equilibrio:
 2da condición de Equilibrio:
  0F










0
0
0
zF
yF
xF



  0













0
0
0
z
y
x




8.  Sumatoria:
 Coseno del doble:
  ....))(2)(1())(1()(11 321
 annnannana
n
  ....))(2)(1())(1()(11 321
 annnannana
n
  )(12 2
 SenCos 

9. Para ángulos pequeños:
  )(12 2
 SenCos 
60 1.04400 0.86602 1.73205
30 0.52200 0.50000 0.57735
15 0.26100 0.25881 0.26794
10 0.17400 0.17364 0.17632
5 0.08700 0.08715 0.08748
4 0.06960 0.06975 0.06992
3 0.05220 0.05233 0.05240
2 0.03480 0.03489 0.03492
1.5 0.02610 0.02617 0.02618
1 0.01740 0.01745 0.01745
0.5 0.00870 0.00872 0.00872
 rad )(Sen )(tg

10.  1.-Entre dos columnas
fue tendido un alambre de
longitud . En el alambre
exactamente al centro,
fue colgado un farol de
masa M. El área de la
sección transversal del
alambre es A, el modulo
de elasticidad es Y.
Determinar el ángulo ,
de pandeo del alambre,
considerándolo pequeño.
2


11.  2.-Se cuelga una viga
de 2000 Kg de dos
cables de la misma
sección, uno de
aluminio y otro de
acero. Al suspenderla,
ambos cables se
estiran lo mismo.
Calcular la tensión
que soporta cada uno.

12.  3.-En el sistema mostrado, ¿Cuánto bajara el
peso W respecto a la posición en la cual el
tensor no estaba deformado?.

13.  4.-Se tiene una columna de largo L, sección
transversal A, densidad , modulo de Young Y. se
jala sobre un piso liso de la manera como se
muestra en la figura. Calcule cuanto estira el
cuerpo.
