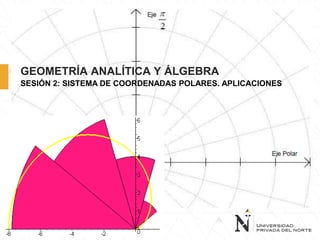
Este documento trata sobre el sistema de coordenadas polares y sus aplicaciones. Explica cómo las coordenadas polares simplifican cálculos en levantamientos topográficos y navegación marítima al utilizar ángulos y distancias. También presenta ejemplos de conversiones entre coordenadas polares y cartesianas, ecuaciones de curvas como circunferencias, parábolas, elipses e hipérbolas en el sistema polar, y resuelve un problema de aproximar el contorno de una piscina usando la ecuación de una cardiode.

1. GEOMETRÍA ANALÍTICA Y ÁLGEBRA
SESIÓN 2: SISTEMA DE COORDENADAS POLARES. APLICACIONES

2. CASO 1: APLICACIONES EN LEVANTAMIENTOS
TOPOGRÁFICOS
Las coordenadas polares tienen
mucha importancia a la
ingeniería civil, sobre todo en
casos de levantamientos
topográficos, pues su uso es por
medio del sistema de
coordenadas polares.
204/06/2015

3. Las coordenadas polares son interesantes al estudiar fenómenos relacionado
con distancias y ángulos .
Veamos a enumerar algunos:
CASO 2: EN LA NAVEGACIÓN
Ecuaciones de curvas: las coordenadas polares simplifican la ecuación
de ciertas curvas.
Navegación marítima: como la
navegación marítima se basa en
ángulos y distancias la utilización
de las coordenadas polares
simplifica mucho los cálculos
necesarios para realizar dicha
actividad.

4. ¿SABÍAS QUE?: En Los micrófonos, la directividad es la
característica que nos indica desde qué dirección recoge
mejor el sonido.
Micrófonos Unidireccionales.
Dentro de esta categoría se
encuentra el patrón más extendido
y usado en la mayor parte de
micrófonos, el cardiode. Como su
nombre indica, tiene forma de
corazón. Estos micrófonos reciben
mejor la señal al hablarles de
frente, aunque siempre recogen un
poco de sonido por la parte trasera
y lateral.
¿cómo calcular el área de un cardiode?

5. Un ingeniero civil desea construir
una piscina en su finca, y quiere el
modelo como se muestra en la
siguiente figura:
Si las únicas medidas que se
conocen son las que se señalan en
la figura
6 m
PROBLEMATIZACIÓN
¿Habrá alguna curva paramétrica
que se aproxime a la curva mostrada?
¿Habrá alguna cónica ya estudiada
que le permite aproximar el contorno
de la curva?
4m 6m

6. ¿Qué método es más adecuado para graficar una ecuación paramétrica?
RESPONDA A LAS SIGUIENTES INTERROGANTES
 ¿Cómo transformas una ecuación cartesiana a paramétrica o viceversa?
 ¿Qué es una ecuación polar?
 ¿Qué ecuación polar corresponde al contorno de la piscina?
 ¿Cómo graficas una ecuación polar?

7. LOGRO DE SESIÓN
Al finalizar la sesión, el estudiante
grafica y convierte curvas de
coordenadas polares a cartesianas y
viceversa, aplicando para ello
métodos gráficos por tabulación y/o
graficadora a las ecuaciones polares.

8. Los puntos en coordenadas polares tienen la forma P(r, θ),
donde r = radio, es la distancia dirigida desde el origen (0, 0)
al punto P, un punto dado en el plano y θ el ángulo. Si el lado
móvil del ángulo se mueve en dirección contraria al
movimiento de las manecillas del reloj, entonces la dirección
del ángulo es positiva.
Si el lado móvil del ángulo se mueve siguiendo el movimiento
de las manecillas del reloj, entonces la dirección del ángulo es
negativa.
COORDENADAS POLARES

9. COORDENADAS POLARES
9
A cada punto P(x,y) en el plano se le
asignan coordenadas polares (r,θ),
como sigue:
r = distancia dirigida de O a P
θ = ángulo dirigido, en sentido
contrario al de las manecillas del
reloj desde el eje polar hasta el
segmento OP
Ejemplo:

10. SISTEMA POLAR O ROSETA POLAR O PLANO POLAR
10
• Sistema Polar o Plano Polar consiste de circunferencias
concéntricas al origen y rectas concurrentes al origen con
diferentes ángulos de inclinación.
• Al eje horizontal se llama “eje polar”, y al eje vertical se llama “eje
π/2”. El punto de intersección entre estos dos ejes se lo llama
“Polo”.
30°
+
-
-
-

Fig: 2,4. Ángulo positivo
0°
90°
180°
60°
120°
150°
210°
240°
270°
300°
330°
360°

11. EJEMPLOS
11
Se muestra tres puntos en el sistema de coordenadas polares y vamos a
localizarlos a una retícula de circunferencias concéntricas interceptadas por
rectas radiales que pasan por el polo.

12. 12
De coordenadas
rectangulares a
polares
2 2
r x y
y
arctg
x

  

  
  
 
De coordenadas
polares a rectangulares
cosx r
y rsen





   , ,P r P x y 
y
x
r

CONVERSIÓN DE COORDENADAS POLARES A CARTESIANAS
Y VICEVERSA

13. 13
Encuentre las coordenadas polares del punto P(1,1).
Solución:
Representando el punto en el plano cartesiano, se tiene:
EJEMPLO 1

14. 14
Utilizando las transformaciones:
Además se podría utilizar otras equivalencias polares:
2 2 2 2
1 1 2
1
1 4
r x y r
y
arctgarctg
x


     
 
    
     
   
7 5 3
2, 2, 2, 2,
4 4 4 4
          
              
       
SOLUCIÓN DEL EJEMPLO 1

15. 15
EJEMPLO 2
a) Dado el punto    , 2,r  
cos 2cos 2
2 0
x r
y rsen sen
 
 
   

  
Luego, el punto coordenado es:    , 2,0x y  
b) Dado el punto  , 3,
6
r


 
  
 
3
3cos
6 2
3
3
6 2
x
y sen



 

  

Luego, el punto coordenado es:
 
3 3
, ,
2 2
x y
 
   
 
CONVERSIONES DE POLARES A CARTESIANAS

16. 16
EJEMPLO 3
a) Dado el punto en el segundo cuadrante    , 1,1x y  
 
3
tan 1 arctan arctan 1
4
y y
x x

  
 
         
 
Luego, el punto coordenado es:    , 2,0x y  
Como se eligió el ángulo en el mismo cuadrante que , se debe usar un
valor positivo para r.
 ,x y
2 2 2 2
( 1) (1) 2r x y     
Esto implica que un conjunto de coordenadas polares es  
3
, 2,
4
r


 
  
 

17. b) Dado que el punto se encuentra en el eje positivo, se elige
, y un conjunto de coordenadas polares es
   , 0,2x y 
, 2
2
y r

  
 , 2,
2
r


 
  
 

18. COORDENADAS POLARES DE LAS
CÓNICAS
• Recta
• Circunferencia
• Parábola, Elipse, Hipérbola
• Cardioide, etc

19. RECTAS QUE CONTIENEN AL POLO
y
x

y xm
y xm
Resulta, finalmente . 
Ejemplo. y
x

3y x
 
60
3 3y x arctg

  
 

20. r = 3sec r = 3cosec
RECTAS QUE CONTIENEN AL POLO

21. RECTAS QUE NO CONTIENEN AL POLO
Del triángulo tenemos:
Por tanto, sería:
 cos
d
r
 


 cos
d
r
  

22. • La ecuación: r = 2
CIRCUNFERENCIA CON CENTRO EN EL POLO

23. CIRCUNFERENCIA QUE PASA POR EL POLO

24. Se define a la parábola ( e =1), a la elipse ( 0 < e < 1)
y a la hipérbola ( e >1) como el conjunto de puntos
del plano tales que:
( , )
( , )
d P F
e
d P l

FORMA GENERAL DE LAS CÓNICAS

25. De acuerdo a lo mencionado se tiene:
Cónica horizontal derecha
Cónica horizontal izquierda
Cónica vertical arriba
Cónica vertical abajo
PARÁBOLA, ELIPSE E HIPÉRBOLA
 1 cos
ed
r
e  

 
1. Si tenemos
2. Si tenemos
3. Si tenemos
4. Si tenemos
0  
 1 cos
ed
r
e 


 
 1 cos
ed
r
e 


2

 
 1
ed
r
esen 


3
2

 
 1
ed
r
esen 



26. EL CARDIOIDE
2626Cardioide horizontal Cardioide vertical
Podemos observar que se distingue una figura como de un
corazón, razón por la cual se llama este gráfico cardioide.

27. CURVAS IMPORTANTES

28. Un ingeniero civil desea construir
una piscina en su finca, y quiere un
modelo como se muestra en la
siguiente figura:
Si las únicas medidas que se
conocen son las que se señalan,
diga: 4 m y 6m
6 m
PROBLEMATIZACIÓN: SOLUCIÓN
¿Habrá alguna curva paramétrica
que ayude a aproximar la medida del
contorno?
¿Habrá alguna cónica ya estudiada
que me permite aproximar el
contorno?

29. Solución:
Dada la ecuación de la cardiode de
la forma:
6 m
PROBLEMATIZACIÓN: SOLUCIÓN

30. Ejercicios
1. Graficar los siguientes puntos en un
sistema de coordenadas polares:
a) b)
2. Determinar la distancia entre los puntos
2,
3
 
 
 
3
3,
2
 
 
 
 1 1,P r   2 2,Q r 
.

31. REFERENCIAS BIBLIOGRAFICAS
N° CÓDIGO AUTOR TITULO EDITORIAL AÑO
1 516.3 OROZ
OROZCO MAYREN,
GILBERTO
Geometría Analítica: Teoría y
Aplicaciones
Trillas 2007
2
516.182
ESPI/E
ESPINOZA, RAMOS
EDUARDO
Geometría Vectorial en R3 2004, s.n. 2004
3
516.32
ESPI
ESPINOZA RAMOS,
EDUARDO
Geometría Analítica Plana
: Teórico-Práctico
S.n 2007