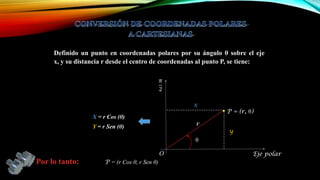
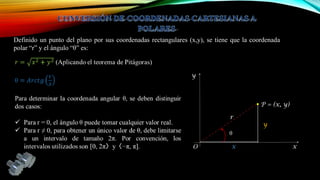
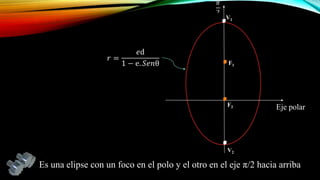
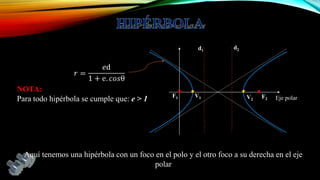
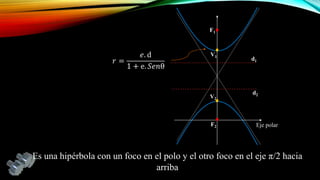
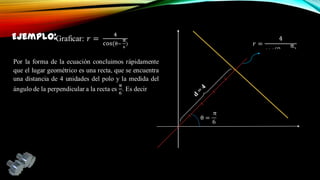
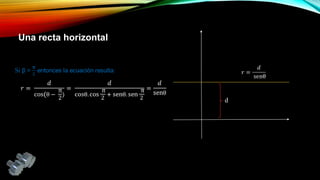
El documento presenta la geometría analítica plana enfocándose en el sistema de coordenadas polares, definiendo cómo se representa la posición de un punto en un plano mediante el par ordenado (r, θ). Se detallan transformaciones entre coordenadas polares y cartesianas, así como la clasificación de cónicas según su excentricidad. Además, se incluyen ejemplos prácticos y aplicaciones de estas transformaciones en geometría.

1. GEOMETRÍA ANALÍTICA PLANA
P=(r, θ)
r
θ
0
Eje Polar

2. COORDENADAS POLARES
DEFINICIÓN:
Es un sistema que define la posición de un punto en un
espacio bidimensional el cual está determinado por un
ángulo y una distancia.
Para todo punto P en el plano se le asignan coordenadas
polares (r, ) donde r es la distancia de P al origen O, y θ es
el ángulo formado entre el eje polar y la recta dirigida OP.
Si el punto P coincide con el origen, r = 0 y el ángulo θ no
tendrá un valor determinado

3. Donde:
P=(r, θ)
r
r = Distancia dirigida OP
θ = Ángulo dirigido, desde el
eje
polar al segmento OP
θ
0
Eje Polar
Si P es cualquier punto del plano, r la distancia de O a P, y θ (medido en radianes) el ángulo
formado por el eje polar y la recta OP. Entonces P está representado por el par ordenado (r, θ)
que son las coordenadas polares de P.
Por convención, θ es positivo si se mide en dirección contraria al movimiento de las agujas
del reloj y θ es negativo si se mide a favor del movimiento de las agujas del reloj.

4. Ejemplo:
El punto P1 se puede expresar
en las formas (-3,2π/3) o
(3,5π/3) o (3,- π/3).
P1
P1

5. PLANO POLAR
P1
P2
Eje polar
P3
P4
En el papel coordenado polar se ha trazado los siguientes puntos: P1 = (6,
P3 = (6,7π/6) y P4 = (5,11π/6)
π/4), P2 = (2,3π/4),

6. TRANSFORMACIÓN DE COORDENADAS POLARES A
CARTESIANAS Y VICEVERSA
Cartesiana a polar
y
P(r, θ)
P(x, y)
Polar a cartesiana
r
Y = r.Sen θ
θ
0
X = r.Cos θ
X = Eje Polar

7. Definido un punto en coordenadas polares por su ángulo θ sobre el eje
x, y su distancia r desde el centro de coordenadas al punto P, se tiene:
x
X = r Cos (θ)
r
Y = r Sen (θ)
.
P = (r, θ)
y
θ
O
Por lo tanto:
P = (r Cos θ, r Sen θ)
Eje polar

8. EJEMPLO 01:
Hallar las coordenadas rectangulares del punto P cuyas coordenadas polares son (4,
r = 4; θ = π/3
x = r Cos θ,
y = r Sen θ
x = 4Cos π/3,
y = 4 Sen 2π/3
x = 4(0.5)
y = 4(0.87)
x = 2,
y = 3.46
P = (2, 3.46)
x
.
π/3).
P = (r, 2π/3)
4
y
π/3
O
POR LO TANTO: el punto P en el sistema de coordenadas polares es (4,
coordenadas cartesianas es (2,3.46).
Eje polar
π/3), y en el sistema de

9. EJEMPLO 02:
Dada la ecuación polar r(3 - 2cosθ) = 2. Obtener la ecuación cartesiana.
POR LO TANTO: La ecuación obtenida representa a una elipse

10. Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada
polar “r” y el ángulo “θ” es:
y
.
r
P = (x, y)
y
θ
O
x
x

11. y
.
r
θ
O
1
x

12. EJEMPLO 02
Obtener la ecuación polar de la curva cuya ecuación es: 3 x + 4 y + 1 = 0 .

13. Circunferencia con centro en el polo
Su ecuación es: X2 + y2 = a2
.
Aplicando transformaciones tenemos:
x2 + y2 = a2
r=a
θ
Eje polar
De lo cual concluimos que:

14. Circunferencia con centro exterior al polo
P(r,θ)
.
a
Sea C(c, a) el centro de una circunferencia
cualquiera de radio “a”. Sea P = (r, θ) un punto
cualquiera de la circunferencia. Tracemos el radio
CP y los radios vectores de P y C, formando así el
triángulo OPC. De este triángulo, por la ley de
cosenos, resulta:
. C(c, a)
r
c
.
0
Eje polar

15. Directriz (l )
Clasificación de las cónicas de acuerdo con la
excentricidad
El conjunto de todos los puntos P con una
determinada excentricidad es una cónica.
1. La cónica es una elipse si 0 < e < 1.
2. La cónica es una parábola si e = 1.
3. La cónica es una hipérbola si e > 1.
Donde “e” es la excentricidad
.
C
r
D
.
V
.
.
O
B
Eje polar

17. Parábola cóncava a la izquierda
Directriz
X=d
Directriz vertical a la derecha
del polo
F
V
Eje polar
NOTA:
Para todo parábola se cumple que: e = 1
d

18. Parábola cóncava a la derecha
Directriz
X=-d
Directriz vertical a la izquierda
del polo
V
d
F
Eje polar

19. Parábola cóncava hacia abajo
Directriz
y=d
d
Directriz horizontal arriba del
polo
V
F
Eje polar

20. Parábola cóncava hacia arriba
F
Directriz horizontal abajo del
polo
Eje polar
d
V
Directriz
y=-d

21. l
l
una elipse con un foco en el polo y el otro a su
izquierda en el eje polar
.
V2
.
F2
NOTA:
Para todo elipse se cumple que: 0 < e < 1.
.
F1
.
V1
Eje polar

22. l
l
.
V2
F2
.
.
.
F1
V1
Eje polar
Es una elipse con un foco en el polo y el otro a su derecha en el eje polar

23. .
V1
.
F1
Eje polar
.
F2
.
V2
Es una elipse con un foco en el polo y el otro en el eje π/2 hacia abajo

24. .
V1
.
.
F1
F2
Eje polar
.
V2
Es una elipse con un foco en el polo y el otro en el eje π/2 hacia arriba

25. d1
NOTA:
Para todo hipérbola se cumple que: e > 1
. .V
F
1
1
d2
.
V2
.F
2
Eje polar
Aquí tenemos una hipérbola con un foco en el polo y el otro foco a su derecha en el eje
polar

26. d1
.
F
1
.V
1
d2
.
V
2
.F
2
Eje polar
Es una hipérbola con un foco en el polo y el otro foco a su izquierda
en el eje polar

27. F1
.
.
V
1
.
V2
.
F
2
d1
d2
Eje polar
Es una hipérbola con un foco en el polo y el otro foco en el eje π/2 hacia
arriba

28. .
F1
.
V
1
.
Eje polar
d1
d2
V2
F2
.
Es una hipérbola con un foco en el polo y el otro foco en el eje π/2
hacia abajo

29. Recta que contiene al polo
. P(r, θ)
Y = mx
Θ=β
0
Eje polar

30. RECTA QUE NO CONTIENE AL POLO Y SE ENCUENTRAN A UNA
DISTANCIA “d” DEL POLO
P(r, θ)
r
r
θ-β
d
θ-β
θ
0
β
d

31. Ejemplo:

32. UNA RECTA VERTICAL
d
Eje polar

33. Una recta horizontal
d

34. ROSA DE CUATRO HOJAS/PÉTALOS
PARÁBOLA
CIRCUNFERENCIA
y
x
LEMNISCATA
CARDIOIDES
ESPIRAL

35. GRACIAS
GENIOS POR SU
ATENCIÓN
Autor: Richard Portilla Pérez
Universidad Nacional de Cajamarca