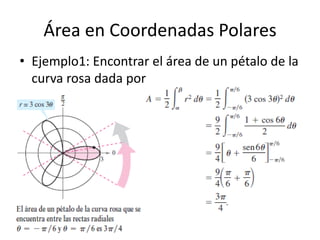
Este documento presenta una clase sobre coordenadas polares. La clase cubrirá el sistema de coordenadas polares, cómo expresar coordenadas y ecuaciones rectangulares en forma polar y viceversa, y cómo trazar gráficas de ecuaciones dadas en forma polar. La clase también cubrirá cómo calcular el área de una región limitada por una gráfica polar.

1. Prof. Emma Yendis
Clase del 11/05/2011 al 18/05/2011
COORDENADAS POLARES

2. Objetivos de la clase
• Comprender el sistema de coordenadas
polares.
• Expresar coordenadas y ecuaciones
rectangulares en forma polar y viceversa.
• Trazar la gráfica de una ecuación dada en
forma polar

3. Coordenadas Polares
Para formar el sistema de
coordenadas polares en el
plano, se fija un punto O,
llamado polo (u origen), y
a partir de O, se traza un
rayo inicial llamado eje
polar, como se muestra en
la figura. A continuación, a
cada punto P en el plano
se le asignan coordenadas
polares (r, ), como sigue:

4. Coordenadas Polares
•  es positivo cuando se mide en sentido contrario de las
agujas del reloj y negativo cuando se mide en sentido de las
manecillas
• El ángulo asociado con el punto no es único.
Ejemplo:
• Pueden tener valores r negativos.

5. Trazo de puntos en
Coordenadas Polares
• Ejemplos: Localice los puntos del siguiente
conjunto de coordenadas:

6. Relación entre Coordenadas Polares y cartesianas
Por identidades trigonométricas:

7. Relación entre Coordenadas Polares y Cartesianas
• Ecuaciones Equivalentes

8. Conversión de Coordenadas
• Encuentre una • Sustituya las siguientes
coordenada polar para el ecuaciones polares por sus
círculo
equivalentes cartesianas

9. Conversión de Coordenada Polar a Rectangular.

10. Trazo de Gráficas en
Coordenadas Polares
• Dibujar la gráfica de

11. Trazo de Gráficas en
Coordenadas Polares

12. Gráficas polares especiales
• Varios tipos importantes de gráficas tienen
ecuaciones que son más simples en forma
polar que en forma cartesiana. Por ejemplo, la
ecuación polar de un círculo de radio a y
centro en el origen es simplemente r= a.

13. Gráficas polares especiales

14. Gráficas polares especiales

15. Gráficas polares especiales

16. PLANO r

17. Prof. Emma Yendis
ÁREA EN COORDENADAS POLARES

18. Objetivo de la Clase
Hallar el área de una región limitada
por una gráfica polar.

19. Área en Coordenadas Polares
Obsérvese que el área de un sector circular
de radio r está dada por siempre que
esté dado en radianes.

20. Área en Coordenadas Polares
• Considérese la función dada por donde
es f continua y no negativa en el intervalo dado
por . La región limitada por la gráfica f
de y las rectas radiales.

21. Área en Coordenadas Polares

22. Preliminar

23. Área en Coordenadas Polares
• Ejemplo1: Encontrar el área de un pétalo de la
curva rosa dada por

24. Área en Coordenadas Polares
• EJEMPLO 2.
Hallar el área de la región comprendida entre los
lazos interior y exterior del caracol

25. Área en Coordenadas Polares

26. Referencias Bibliográficas
• Larson, R. y otros. Cálculo y Geometría
Analítica. Volumen II, 10ma. Edición.
– Capítulo 10, pág 739-740
• Thomas, G. Calculus. Part Two, Multiple
Variable. 11th Edition.
– Capítulo 10, pág 714-718 y 725 - 727