El documento trata sobre un cuaderno de trabajo de matemáticas para quinto grado de primaria. Presenta una estructura con una introducción, objetivos de aprendizaje, y secciones para demostrar lo aprendido, autoevaluarse y aplicar los conocimientos en ejercicios y problemas. El cuaderno aborda temas como conjuntos, números naturales, operaciones matemáticas, geometría y estadística, con el fin de desarrollar competencias matemáticas de manera secuencial en los estudiantes.

















































































![103
Cuaderno de trabajo
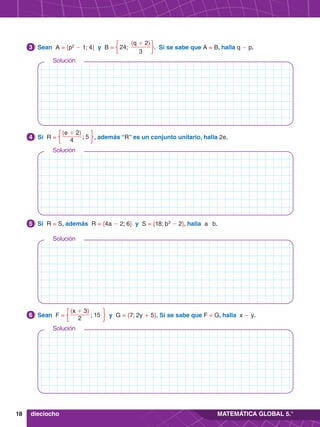
Solución
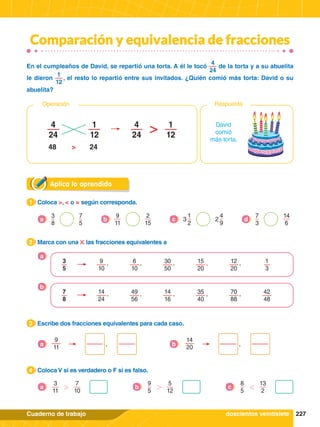
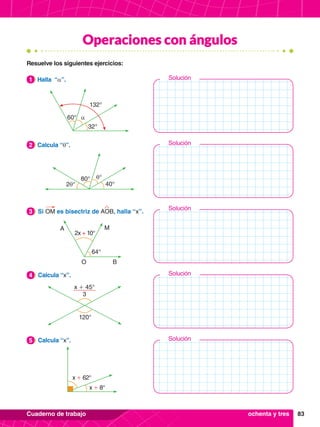
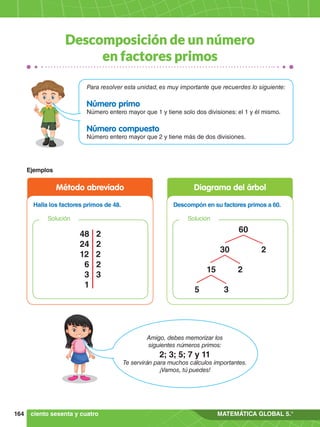
Operaciones combinadas
A + B = 40 + 3 = 43
B = 26
+ 201
- 34
B = 64 + 20 - 81
B = 84 - 81
B = 3
A = 43
- 52
+ 18°
A = 64 - 25 + 1
A = 39 + 1
A = 40
Si A = 43
- 52
+ 18° y B = 26
+ 201
- 34
,
halla A + B.
5
Para resolver operaciones combinadas debes tener en cuenta la jerarquía:
1.° Lo que está dentro de signos de colección
2.° Potencias
3.° Multiplicaciones y divisiones
4.° Sumas y restas de izquierda a derecha
Importante
32
+ 23
+ (120 ÷ 6)
9 + 8 + 20
17 + 20 = 37
1
23
+ [52
- (13 # 4 - 62
)]
8 # [25 - (52 - 36)]
8 # [25 - 16]
8 # 9 = 72
2
48 # 5 + 36
÷ 35
- 25
240 + 3 - 32
243 - 32 = 211
3
(36 ÷ 6 + 52
) + [32
# (102
- 92
)]
(6 + 25) + [9 # (100 - 81)]
31 + 171 = 202
4
6
16 # 3 - 3 # 8 - 550
48 - 24 - 1
24 - 1
23
7
510
58 + 32
- 5 # 6 +
36
32
52
+ 9 - 30 +
36
9
25 + 9 - 30 + 4
34 - 30 + 4
4 + 4
8
ciento tres
Ejemplos](https://image.slidesharecdn.com/cuadernodetrabajo5-210726050045/85/Cuaderno-de-trabajo-5-103-320.jpg)
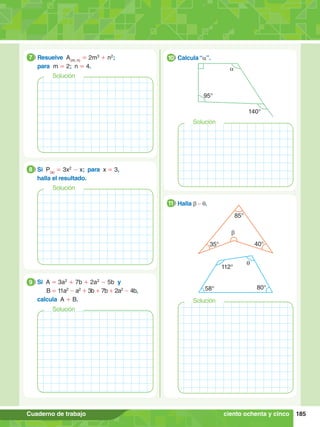
![104 MATEMÁTICA GLOBAL 5.°
Solución
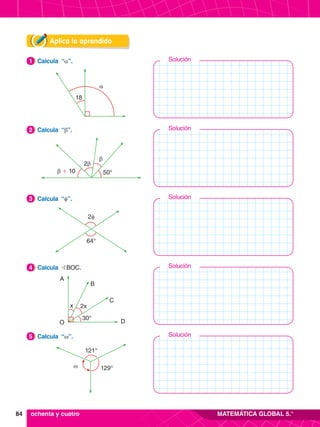
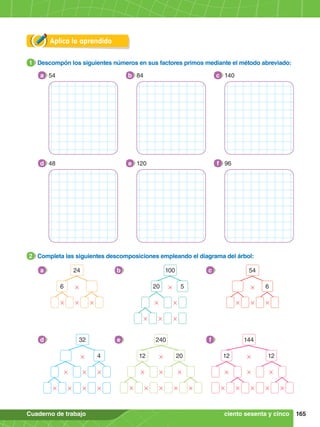
Aplica lo aprendido
1. Resuelve 33
- 24
+ (18 # 22
- 51
).
1
2. Efectúa 53
- 102
+ [31
# (124 ÷ 4 - 52
)].
2
3. Francisco dice:“Si quieres saber cuántos
años tengo, debes resolver la siguiente
operación combinada”:
122
+ 80
- (33
# 22
+ 42
)
3
4. Resuelve 32 ÷ 22
+ 112
- 43
+ (71
# 80
+ 51
).
4
4. Resuelve 53
+ 112
+ (81 - 6 ÷ 2)0
.
5
4. Resuelve
150
+ 1125
+ 82
- 91
3
.
6
ciento cuatro](https://image.slidesharecdn.com/cuadernodetrabajo5-210726050045/85/Cuaderno-de-trabajo-5-104-320.jpg)
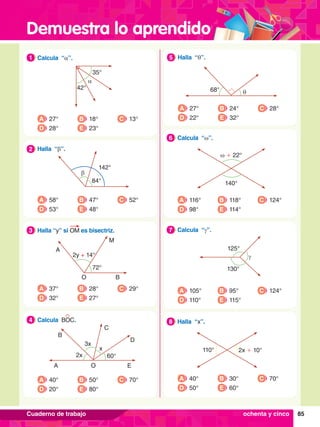
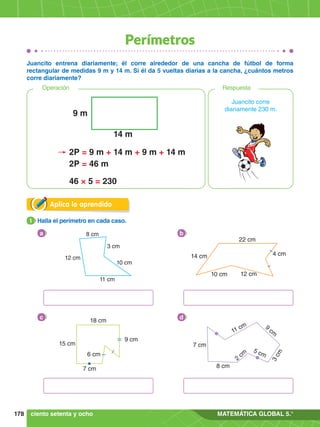
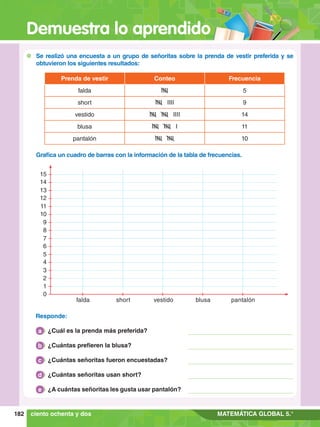
![Demuestra lo aprendido
105
Cuaderno de trabajo
1. Resuelve 36 ÷ 4 + 2 # 72
- 25
.
1
A 10
C 85
E 70
B 75
D 45
5. Efectúa 112
- 33
+ (24
- 32
)2
.
5
A 121
C 143
E 123
B 164
D 133
2. Si A = 52
– 24
+ 70
# 51
y
B = 32
+ (24 ÷ 22
),
halla A + B.
2
A 27
C 35
E 29
B 32
D 28
3. Nico dice: “Yo tengo una cantidad de
juguetes igual al resultado de
33
- 71
+ (14 ÷ 7 + 80
)”.
¿Cuántos juguetes le quedarán a Nico
si él decide regalar a su hermanito
8 juguetes?
3
A 18
B 17
C 15
D 12
E 14
4. Resuelve 43
- 25
+ [23
# (75 ÷ 5 - 51
)].
4
A 112
C 92
E 118
B 114
D 96
6. Si M = 92
- 43
+ (70
# 23
) y
N = 122
- 34
+ 111
,
calcula M + N.
6
A 99
D 79
B 84
E 87
C 69
7
. Micaela dice: “Yo tengo de edad el
resultado de 25 ÷ 5 + (26
- 43
) + 71
y
mi prima es 3 años mayor que yo”. ¿Cuál
es la edad de la prima Micaela?
7
A 11
B 12
C 15
D 14
E 10
4. Resuelve 53
– [82
– 33
– 101
].
9
7
. ¿Cuál es la edad que tengo si dentro de 10
años será igual al doble de mi edad actual?
8
Solución
ciento cinco](https://image.slidesharecdn.com/cuadernodetrabajo5-210726050045/85/Cuaderno-de-trabajo-5-105-320.jpg)
















![123
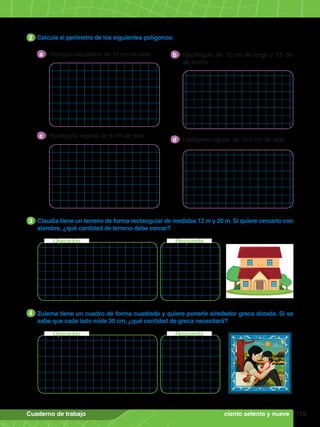
Evalúa tus conocimientos
Cuaderno de trabajo
3. Si P = 48 ÷ 22
+ 14 + 32
y Q = 130 - [72
- 25
] + 111, halla P + Q.
3
2. Efectúa lo siguiente y comprueba:
4
9 0 0 2 5
a b
2. Efectúa lo siguiente:
2
a b
35 ' 7 + (25
- 32
+ 50
) 125 ' 5 + 32
# [62
- (48 '2)]
1. Resuelve las siguientes divisiones y coloca sus elementos.
1
a b
3 5 2 8 1 2 6 5 9 2 3 2
Comprobación
2 0 5 7 1 7
Comprobación
ciento veintitrés
Solución](https://image.slidesharecdn.com/cuadernodetrabajo5-210726050045/85/Cuaderno-de-trabajo-5-123-320.jpg)



















































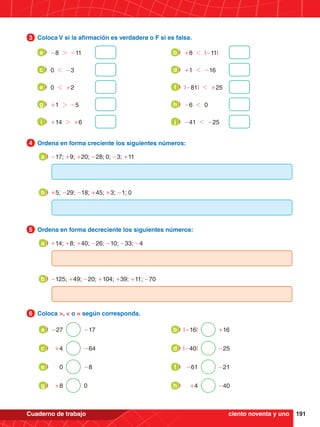




![196 MATEMÁTICA GLOBAL 5.°
1. Si R = (-18) + (-32) - (-50) y
Q = (-25) - (-32) + (+8),
halla el resultado de R + Q.
12
A +25
D -25
B -15
E +15
C +18
1. Coloca V si la afirmación es verdadera o
F si es falsa.
11
(+28) - (-30) = +58
a
(-25) - (-17) = -42
b
(+32) - (+8) = +40
c
(-14) - (+6) = -20
d
1. Efectúa 8 + 4 – [5 – 3 ( 3 ) – 3 (– 5)].
13
1. Efectúa – 3 – 8 + 5 – 16 – 32 + 15.
14
1. Efectúa + 15 + 2 – 17 – 32 + 45 – 3 – 15.
15
1. Efectúa 3 + 4 – 8 – (– 5 + 16) – 32 + 45.
16
1. Un señor tenía una cantidad de dinero,
pero luego le robaron S/ 130. Después le
regalaron S/ 75 y finalmente se encontró
S/ 50. ¿Al final le quedó más o menos
que al principio?
17
Solución
ciento noventa y seis](https://image.slidesharecdn.com/cuadernodetrabajo5-210726050045/85/Cuaderno-de-trabajo-5-196-320.jpg)