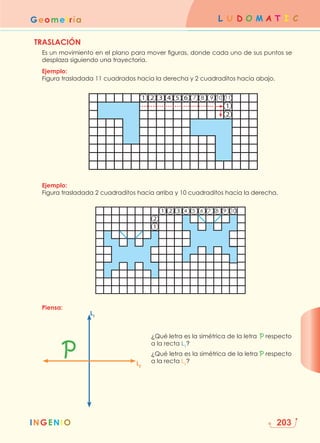
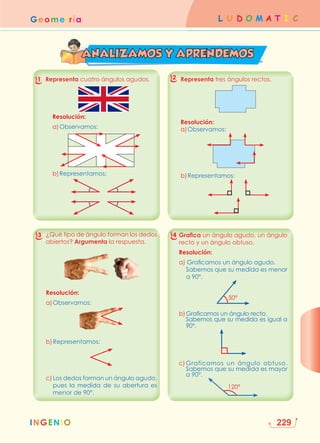
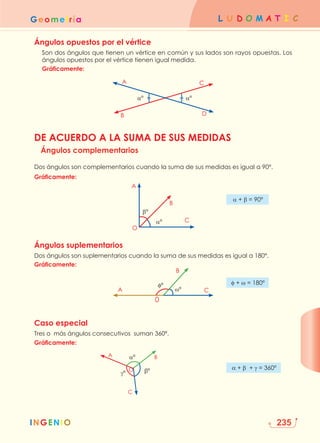
Este documento presenta la información de contacto y los derechos de autor de un libro de texto de matemáticas para cuarto grado de primaria. Incluye los nombres del equipo editorial y de producción, así como detalles sobre la impresión y distribución. Además, ofrece una breve descripción de las secciones y contenidos que componen el libro, centrados en el desarrollo del pensamiento lógico-matemático a través de actividades lúdicas.

1. LÓGICO MATEMÁTICO
Libro de consulta

2. LUDOMATIC 4.O
PRIMARIA
"Desarrolla tu capacidad con ingenio"
Título de la obra
Lógico Matemático. Ludomatic 4.º Grado
Directora editorial
Juana Mery Oblea Acosta
Apoyo editorial:
Elvis Valerio Solari
Carmen Isabel Inca Maldonado
Abel Ricardo Solis Alvarez
Editor
Juan Miranda Tipacti
Corrector de estilo
Roger Aponte Bonifaz
Diseño gráfico y diagramación:
Luisa Haydée Ronceros Ríos
Marco Antonio Lizárraga Podestá
Luis Alexis Tataje Flores
Fotos
Yuri Hernández Oblea
© Derechos de autor reservados
Juana Mery Oblea Acosta
© Derechos de edición reservados
Editorial Ingenio & YHO S.A.C.
Proyecto Editorial N.º 11501001500239
ISBN: 978-612-46772-6-7
Hecho el Depósito Legal en la Biblioteca Nacional del Perú N° 2015-02310
Nueva edición: Febrero 2015
Tiraje: 3000 ejemplares
Editado por:
Editorial Ingenio & YHO S.A.C.
Av. Tacna Nº 407 Of. 301 - Lima
Telefax: (511) 426–4853
www.editorialingenio.pe
E-mail: editorial.ingenio@hotmail.com
Impreso en:
Corporación Gráfica Navarrete S.A.
Carretera Central 759 – km 2 Santa Anita, Lima – Perú Teléfono: 362–0606
Prohibida la reproducción total o parcial de esta obra sin previa
autorización escrita del autor y de la editorial.

3. 3
Conoce tu libro
Conoce tu libro
El aprendizaje que lograrás al trabajar con tu libro LUDOMATIC te brindará herramientas para
dar solución a problemas cotidianos relacionados con las matemáticas.
Tu libro de Matemáticas consta de tres áreas que, mediante las actividades propuestas, te
brindarán estrategias para desarrollar tu pensamiento lógico matemático.
Las imágenes
tienen como
finalidad
promover el
análisis y
reflexión en
los alumnos.
Juegos para experimentar la
matemática de manera lúdica
Situaciones
que promueven
valores y
actitudes
Preguntas del
entorno que
involucran
el desarrollo
de los temas
transversales.
Aprendizajes
esperados que
se alcanzará a
lo largo de la
unidad
Observa la imagen y contesta.
UNIDAD
7
Aprendemos a
Cultivamos Valores
Educación en equidad de géneros
¿Sabes qué es la igualdad de géneros?
¿Hombres y mujeres tienen las mismas oportunidades?
• Educación para la
equidad de géneros
• Tolerancia
• Identificarlasdiferentesformasdeecuaciones.
• Resolver ecuaciones de la forma x + a = b;
x - a = b; ax = b; x/a = b; a x + b = c; a x - b = c.
• Interpretar y plantear ecuaciones.
• Resolver problemas de diferentes contextos
que impliquen el uso de las ecuaciones.
INGENIO
4.° primaria
L U D O M A T I C
194
INGENIO
NOCIONES BÁSICAS
DE GEOMETRÍA
El punto
Se representa por la marca que deja la punta de un lápiz sobre el papel y se denota
con letra mayúscula.
A
Se lee Punto A.
• Línea:
En una sucesión indefinida de puntos, obtenemos líneas que pueden ser rectas,
curvas, quebradas y mixtas.
Gráficamente:
Línea recta Línea curva
Línea mixta
Línea quebrada
TALLER
1
Nociones básicas de geometría
Son los elementos
básicos de la
Geometría.
¿Qué sabemos
del punto, recta
y plano?
¿El horizonte del mar forma una línea recta o curva?
¿El sol nos da la idea de un punto?
Sí, puedo
ver líneas y
curvas.
¿Lucero
observas el
horizonte?
Conflicto
cognitivo
Estructura de
los aprendizajes
esperados.
Sección donde
los estudiantes
ponen en práctica
sus habilidades
y destrezas
adquiridas a través
de situaciones
problemáticas.
INGENIO
L U D O M A T I C
Geometría
219
INGENIO
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1
2
4
3
Indicadores de evaluación
En qué punto está ubicado la pelota.
Argumenta tu respuesta.
1
1
2
3
4
5
y
2 3 4 5 6 7 8 x
0
Determina el valor de verdad de las
siguientes proposiciones.
a)Al eje “x” se le llama también eje
de las ordenadas.
( )
b)El par ordenado es un punto ( )
en el plano cartesiano.
c)El plano cartesiano está ( )
formado por 2 rectas
perpendiculares.
Observa y realiza lo siguiente:
a)Pinta de azul el eje de las abscisas.
b)Pinta de rojo el eje de las ordenadas.
c)Anota el punto donde se ubica la
muñeca.
y
x
1
1
2
3
4
5
6
7
8
2 3 4 5 6 7 8 9 10
0
Desplaza un objeto ubicado en el
punto (4; 3) hacia el punto (x + 2; y – 1).
Comunica su nueva ubicación.
y
x
1
1
2
3
4
5
6
7
2 3 4 5 6 7
0
Desarrollo de
actividades
relacionadas
a situaciones
cotidianas; es
decir, tienen
la oportunidad
de transferir
lo aprendido
a nuevas
situaciones.
Proyectos de
aprendizaje,
en donde los
estudiantes realizan
actividades que
los incitan a usar
sus conocimientos
matemáticos para
resolver problemas
del contexto
cotidiano.
PROYECTO DE APRENDIZAJE N.0
5
INGENIO
FRACCIONES
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1. Situación problemática
En las actividades que realizamos a diario encontramos diversas expresiones que
permiten comunicarnos y manifestar lo que deseamos, por ejemplo: "un cuarto de
pollo, medio litro de limonada, tres cuartos de fideos" etc. Estas expresiones hacen
referencia a las fracciones y por ello es sumamente importante conocerlas.
2. Finalidad
• Reconocer el uso de las fracciones en las actividades que realizamos a diario.
3. Recursos materiales
papelote
regla
cinta adhesiva
plumones
lapiceros
4. Etapas y actividades
5. Evaluación
1.ª etapa
2.ª etapa
Formamos grupos de 4 estudiantes.
Realizamos una lista de expresiones más
comunes donde se utilicen las fracciones.
Escribimos las expresiones en un papelote.
Matematizamos estas expresiones.
Ejemplo:
Un cuarto de pollo = 1/4 de pollo.
Exponen su trabajo y lo pegan en las
paredes del aula.
70
Materiales
concretos
para
manipular
Actividades para
desarrollar las
capacidades. En esta
parte, los estudiantes
exploran, investigan,
representan y
matematizan las
situaciones planteadas.

4. 4
CONTENIDOS
A R I T M É T I C A
1
8
7
6
4
5
3
2
Laboratorio 7: Jugamos con los meses .....................................83
Taller 16: Referentes temporales.................................................84
Taller 17: Equivalencias y canjes de monedas y billetes..........88
Proyecto de aprendizaje: Referentes temporales ...................91
Laboratorio 6: Habilidad numérica ...........................................72
Taller 14: Números decimales.....................................................73
Taller 15: Operaciones con decimales.......................................78
Proyecto de aprendizaje: Números decimales........................81
Laboratorio 5: Razonemos las operaciones combinadas ......58
Taller 11: Operaciones combinadas..........................................59
Taller 12: Fracciones......................................................................62
Taller 13: Operaciones con fracciones .....................................66
Proyecto de aprendizaje: Fracciones........................................70
Laboratorio 4: Armamos un rompecabezas.............................43
Taller 8: Multiplicación en N.........................................................44
Taller 9: Proporcionalidad............................................................49
Taller 10: División en N...................................................................52
Proyecto de aprendizaje: Operaciones con números naturales 56
Laboratorio 3: Jugamos y aprendemos ....................................33
Taller 6: Adición y sustracción.....................................................34
Taller 7: Sucesión con números naturales..................................38
Proyecto de aprendizaje: Números naturales ........................41
Laboratorio 1: Agrupamos los animales ......................................8
Taller 1: Conjuntos ..........................................................................9
Taller 2: Determinación de conjuntos.........................................13
Taller 3: Clases de conjuntos.......................................................16
Proyecto de aprendizaje: Conjuntos.........................................20
Laboratorio 2: Jugamos con números.......................................22
Taller 4: Sistema de numeración decimal..................................23
Taller 5: Descomposición polinómica ........................................27
(aproximación y comparación)
Proyecto de aprendizaje: Sistema de numeración..................31
Reciclar es amar el planeta
Aprendemos a
•
un conjunto y sus elementos.
• Representar l a determinación de u n
conjunto.
•
Cultivamos Valores
• Educación para la
prevención
• Educando para la
gestión de riesgos
Observa la imagen y contesta.
¿Cómo podemos contribuir a conservar nuestro medio ambiente?
¿Sabes qué otros materiales podemos agrupar y reciclar?
UNIDAD
1
Educación en prevención
SISTEMA DE
NUMERACIÓN
Aprendemos a
• Representar números naturales en l a
recta numérica.
• Descomponer números n aturales p or
el v alor d e las cifras y p or n otació n
desarrollada.
• Comparar números naturales.
• Aproximarnúmerosa la decena, centena
y millar más cercano.
Cultivamos Valores
• Educación p ara
gestión de riesgos
• Responsabilidad
Observa la imagen y contesta.
¿Consideras importante los simulacros de sismo?
¿En tu colegio realizan habitualmente simulacros de sismos?
UNIDAD
2
4.° primaria
L U D O M A T I C
32 INGENIO
Vivir en paz
NÚMEROS
NATURALES
Cultivamos Valores
• Educación p ara la
paz
• Tolerancia
Aprendemos a
• Resolverproblemasde adiciónysustracción
de números naturales.
• Interpretar y formular s ucesiones con
números naturales.
Observa la imagen y contesta.
¿Qué entiendes por vivir en paz?
¿Porqué crees que es importante vivir en paz y armonía?
UNIDAD
3
Convivir en igualdad y respeto
Cultivamos Valores
• Educación para la
convivencia,la paz
y la ciudadanía
• Educación para la
paz
Observa la imagen y contesta.
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es muy importante en tu familia?
UNIDAD
4
OPERACIONES
CON NÚMEROS
NATURALES
Aprendemos a
• Resolver e jercicios y problemas con
multiplicación de números naturales.
• Representar y r esolver problemas c on
proporcionalidad.
• Resolver e jercicios y problemas con
división de números naturales.
Educación en derechos humanos
Aprendemos a
• Resolveroperacionescombinadasen IN.
• Reconocer y representar fracciones.
• Calcular l a suma y l a diferencia d e
fracciones h eterogéneas utilizando
fracciones homogéneas.
Cultivamos Valores
• Educaciónpara los
derechoshumanos
• Respeto
Observa la imagen y contesta
.
¿Sabes cuáles son tus derechos como niño y como estudiante?
¿Consideras que es importante conocer los derechos humanos?
UNIDAD
5 FRACCIONES
Cultivamos Valores
• Educación par a
la e quidad d e
géneros
• Tolerancia
Aprendemos a
• Reconocer y utilizar l as unidades de
tiempo.
• Utilizar e quivalencias y c anjes con
monedas y billetes.
• Resolver operaciones d e referentes
temporales.
Observa la imagen y contesta.
¿Sabes qué es la igualdad de géneros?
¿Hombres y mujeres tienen las mismas oportunidades?
REFERENTES
TEMPORALES
Educación en equidad de géneros
UNIDAD
7
UNIDAD
Cultivamos Valores
• Educaciónen valores
y formación ética
• Tolerancia
Aprendemos a
•
decimales.
• Convertirycompararnúmerosdecimales.
• Resolver o peraciones con número s
decimales.
Observa la imagen y contesta.
¿Por qué es importante practicar los valores?
¿En tu vida diaria practicas valores? Indica cuáles.
6
NÚMEROS
DECIMALES
Educación en valores
Cultivamos Valores
• Educación para el
éxito.
• Responsabilidad.
ESTADÍSTICA
Aprendemos a
• Ordenar y representar cuadros de doble
entrada.
•
y pictogramas.
Observa la imagen y contesta.
¿Qué actitudes crees que debes tener para lograr el éxito?
Educación para el éxito
UNIDAD
8
Laboratorio 8: Jugamos con los dados .....................................93
Taller 18: Tabla de doble entrada .............................................94
Taller 19: Gráfico de barras y pictogramas...............................97
Taller 20: Sucesos y probabilidades.......................................... 101
Proyecto de aprendizaje: Estadística ...................................... 104

5. 5
Á L G E B R A
1
8
7
6
4
5
3
2
Laboratorio 1: Formamos cuadrados...........................................106
Taller 1: Potenciación.....................................................................107
Taller 2: Propiedades de la potenciación....................................110
Taller 3: Radicación........................................................................113
Proyecto de aprendizaje: Presupuesto para enlosar el aula....116
Laboratorio 2: Formamos expresiones con números y letras.....118
Taller 4: Término algebraico...........................................................119
Taller 5: Clases de expresiones algebraicas................................122
Proyecto de aprendizaje: Expresiones algebraicas en la vida diaria.....125
Laboratorio 3: Completamos el tablero......................................127
Taller 6: Valor numérico de una expresión algebraica..............128
Taller 7: Términos semejantes.........................................................131
Taller 8: Reducción de términos semejantes...............................134
Proyecto de aprendizaje: Calculamos valores numéricos........137
Laboratorio 4: Jugamos con dados.............................................139
Taller 9: Grado de un monomio....................................................140
Taller 10: Grado de un polinomio.................................................143
Proyecto de aprendizaje: Convivencia en la escuela..............146
Laboratorio 5: Volteamos tarjetas................................................148
Taller 11: Adición y sustracción de expresiones algebraicas....149
Taller 12: Operaciones combinadas ...........................................152
Proyecto de aprendizaje: En el mercado...................................155
Laboratorio 6: Ganamos tarjetas..................................................157
Taller 13: Multiplicación de un número por un polinomio..........158
Taller 14: Multiplicación de un monomio por un monomio.......161
Taller 15: Multiplicación de un polinomio por un monomio......164
Proyecto de aprendizaje: Elaboramos presupuestos................167
Laboratorio 7:Transformamos números........................................169
Taller 16: Ecuaciones de la forma: x + a = b ; x – a = b ; ax = b ; x/a = b...........170
Taller 17: Ecuaciones de la forma: ax + b = c ; ax – b = c.................174
Taller 18: Planteo de ecuaciones..................................................177
Proyecto de aprendizaje: Las ecuaciones en la vida diaria....180
Laboratorio 8: Balanceamos números.........................................182
Taller 19: Inecuaciones de la forma: x + a < b ; x + a > b.....................182
Taller 20: Inecuaciones de la forma: ax + b < c ; ax – b > c ; ax + b > c ; ax – b > c......187
Proyecto de aprendizaje: Las ecuaciones en la vida diaria....191
Observa la imagen y contesta
UNIDAD
1
Reciclar es amar al planeta
¿Sabes qué es reciclar?
¿Qué formas de reciclaje conoces?
¿Qué podemos hacer para preservar nuestro planeta?
Aprendemos a
Cultivamos Valores
• Educación para la
conciencia ambiental
• Responsabilidad
• los elementos de la potenciación
y la radicación.
• Aplicar las propiedades de la potenciación.
• Reconocer la relación entre los elementos
de la potenciación y radicación.
• Resolver problemas de diferentes contextos
que impliquen el uso de la potenciación
y la radicación.
Observa la imagen y contesta
UNIDAD
2
Aprendemos a
Cultivamos Valores
Estar prevenidos
• Educación para la
gestión de riesgos
• Responsabilidad
¿Sabes lo que es estar prevenidos frente a un sismo?
¿En tu colegio hay zonas de seguridad en caso de sismo?
•
algebraica.
•
acuerdo al número de términos.
• Expresar mediante lenguaje algebraico
enunciados en lenguaje usual.
• Resolver problemas de diferentes contextos
que impliquen el uso d e las expresiones
algebraicas.
EXPRESIONES
ALGEBRAICAS II
Cultivamos Valores
Educación para
la paz
Tolerancia
Aprendemos a
• Determinar el valor numérico de una expresión
algebraica.
•
• Resolver problemas de diferentes contextos que
impliquenel uso del valor numérico y los términos
semejantes.
Observa la imagen y contesta
¿Qué entiendes por vivir en paz?
¿Conoces cuál es el símbolo de la paz?
¿Cómo crees tú que podemos vivir en el mundo en paz y armonía?
Vivir en paz
Vivir en paz
UNIDAD
3
4.° primaria
L U D O M A T I C
Aprender a convivir
Cultivamos Valores
Educación para la
convivencia, la paz
y la ciudadanía
Tolerancia
GRADO DE UN
POLINOMIO
Aprendemos a
monomio y un polinomio.
Determinar el grado relativo y absoluto de un
monomio y un polinomio.
Resolver situaciones problemáticas aplicando
el grado de un monomio y un polinomio.
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es muy importante en tu familia?
UNIDAD
4
UNIDAD
5
Educación en derechos humanos
OPERACIONES CON
EXPRESIONES
ALGEBRAICAS I
Cultivamos Valores
• Educación para los
derecho humanos
• Respeto
Aprendemos a
• Reducir operaciones de adición y sustracción con
expresiones algebraicas.
• Plantear y resolver operaciones combinadas de
adición y sustracción con expresiones algebraicas.
• Resolver situaciones problemáticas que requieran
la aplicación de las operaciones de adición y
sustracción con expresiones algebraicas.
Observa la imagen y contesta
¿Sabes qué es la Declaración Universal sobre los Derechos Humanos?
¿Cuáles son tus derechos?
¿Cuándo se aprobó la Declaración Universal de Derechos Humanos?
ÁREA
VERD
E
Educación en valores
OPERACIONES
CON EXPRESIONES
ALGEBRAICAS II
Cultivamos Valores
• Educación en Valores y
Formación Ética
• Tolerancia
Aprendemos a
• Realizar diferentes tipos de multiplicación con
monomios.
• Reducir operaciones con multiplicaciones de
monomios.
• Resolver p roblemas d e diferentes contextos
que i mpliquen e l uso d e la multiplicación de
monomios.
Observa la imagen y contesta
¿Qué son los valores?
¿Qué valores practicas en casa y en el colegio?
¿Por qué son importantes los valores en nuestra convivencia diaría?
UNIDAD
6
Observa la imagen y contesta
UNIDAD
7
Aprendemos a
Cultivamos Valores
Educación en equidad de géneros
¿Sabes qué es la igualdad de géneros?
¿Hombres y mujeres tienen las mismas oportunidades?
• Educación para la
equidad de géneros
• Tolerancia
• las diferentesformasdeecuaciones
.
• Resolver ecuaciones de la forma x + a = b
;
x - a = b; ax = b; x/a = b; a x + b = c; a x - b = c.
• Interpretar y plantear ecuaciones.
• Resolver problemas de diferentes contextos
que
impliquen el uso de las ecuaciones.
Educación para el éxito
INECUACIONES
Cultivamos Valores
• Educación para el
éxito
• Respeto
Observa la imagen y contesta
¿Qué entiendes por tener éxito?
¿Es necesario la perseverancia para lograr el éxito ?
¿Qué debo hacer para triunfar en la vida?
Aprendiendo a
•
• Resolver diferentes tipos de inecuaciones.
• Interpretar y plantear inecuaciones.
• Resolver problemas de diferentes contextos que
• impliquen el uso de las inecuaciones.
UNIDAD
8

6. 6
G E O M E T R í A
1
8
7
6
4
5
3
2
Laboratorio 1: Puntos y cuadrados............................................193
Taller 1: Nociones básicas de geometría...................................194
Taller 2: Posiciones de recta en el plano...................................198
Taller 3: Simetría.............................................................................202
Proyecto de aprendizaje: La importancia de las líneas en mis dibujos..... 206
Laboratorio 2: Tres en raya..........................................................208
Taller 4: Segmentos de recta.......................................................209
Taller 5: Punto medio de un segmento......................................213
Taller 6: Plano cartesiano.............................................................217
Proyecto de aprendizaje: Uso de segmentos...........................220
Laboratorio 3: Diseñamos el transportador...............................222
Taller 7: Medición de ángulos......................................................223
Taller 8: Clasificación de ángulos I..............................................227
Proyecto de aprendizaje: Ángulos.............................................231
Laboratorio 4: Sumamos y restamos ángulos............................233
Taller 9: Clasificación de ángulos II.............................................234
Taller 10: Operaciones con ángulos...........................................238
Proyecto de aprendizaje: Ángulos.............................................242
Laboratorio 5: Armamos triángulos.............................................244
Taller 11: Triángulos I......................................................................245
Taller 12: Triángulos II.....................................................................249
Proyecto de aprendizaje: Triángulos..........................................253
Laboratorio 6: Formamos polígonos...........................................255
Taller 13: Cuadriláteros.................................................................256
Taller 14: Propiedades de los cuadriláteros...............................260
Proyecto de aprendizaje: Cuadriláteros....................................263
Laboratorio 7: Jugamos con pentominós..................................265
Taller 15: Unidad de medida: longitud.......................................266
Taller 16: Perímetro........................................................................270
Taller 17: Áreas...............................................................................273
Proyecto de aprendizaje: Perímetros.........................................276
Laboratorio 8: Construyamos poliedros.....................................278
Taller 18: Poliedros y cuerpos redondos.....................................279
Taller 19: Sólidos geométricos: volumen.....................................283
Proyecto de aprendizaje: Sólidos geométricos .......................287
Observa la imagen y contesta
UNIDAD
1
Aprendemos a
Cultivamos Valores
Reciclare sa mar el planeta
• Responsabilidad
• Educación par a
la c oncienci a
ambiental
• Entender y conocer los elementos básicos
de la geometría.
• Reconocer la idea de punto.
•
• Construir y representar rectas p aralelas ,
secantes y perpendiculares.
¿Cómo podemos contribuir a conservar nuestro medio ambiente?
¿Qué otros materiales podemos agrupar y reciclar?
Observa la imagen y contesta
UNIDAD
2
Aprendemos a
Cultivamos Valores
Educación para la prevención
Educación para la prevención
¿Sabes lo que es estar prevenidos frente a un sismo?
¿En tu colegio hay zonas de seguridad en caso de sismo?
• Educación para l a
prevención
• Educación para l a
gestión de riesgos
• Comprender la de un segmento
de recta.
• Realizar operaciones de adición y
sustracción con segmentos de recta.
• el punto medio en el segmento.
Observa la imagen y contesta
UNIDAD
3
Aprendemos a
Cultivamos Valores
Educación para la paz
¿Qué entiendes por vivir en paz?
¿Cómo crees tú que podemos vivir en un mundo de paz y armonia?
• Educación para l a
paz
• Tolerancia
•
• Representar la medida de los ángulos.
•
Observa la imagen y contesta
UNIDAD
4
Aprendemos a
Cultivamos Valores
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es importante en tu escuela? ¿Por qué?
• Educación para la
c onvivencia, la
paz ylaciudadanía
•
de los ángulos.
• Identificar, i nterpretar y r esolve r
operaciones con ángulos.
• Aplicar las propiedades para la
resolución de problemas.
Convivir en igualdad y respeto
TRIÁNGULOS
Educación en derechos humanos
Cultivamos Valores
• Educaciónpara los
derechos humanos
• Respeto
Aprendemos a
• Reconocera lostriángulosen nuestro
entorno y su importancia.
• y los .
s
o
l
u
g
n
á
i
r
t
Observa la imagen y contesta
Sabes qué es la Declaración Universal de los Derechos Humanos.
Conoces cuáles son tus derechos.
UNIDAD
5
UNIDAD
Educación en valores
Cultivamos Valores
• Educación en
Valores yFormación
Ética
• Tolerancia
Aprendemos a
• r
e
c
o
n
o
c
e
R y los elementos del
cuadrilátero.
• Aplicar y argumentar las propiedades
de los problemas.
Observa la imagen y contesta
¿Qué valores prácticas en casa y en el colegio?
¿Por qué son importantes los valores en nuestra convivencia diaría?
6 CUADRILÁTEROS
PERÍMETROS
Educación en equidad de géneros
Cultivamos Valores
• Educación para
la e quidad de
géneros
• Tolerancia
Aprendemos a
-
geométricas.
- Calcular el área de las regiones.
Observa la imagen y contesta.
¿Sabes qué es la igualdad de géneros?
¿Los hombres y mujeres tienen las mismas oportunidades?
7
UNIDAD
Cultivamos Valores
• Educación para el
éxito
• Respeto
Aprendemos a
• Reconocer los elementos básicos de
los poliedros.
• Calcular e l volumen d e los s ólidos
geométricos.
• Construirpoliedros y cuerpos redondos.
SÓLIDOS
GEOMÉTRICOS
Educación para el éxito
UNIDAD
8
Observa la imagen y contesta.
¿Es necesario la perseverancia para lograr el éxito?
¿Qué debo hacer para triunfar en la vida?

7. UNIDAD
1
Reciclar es amar el planeta
Aprendemos a:
•
Interpretar y profundizar la definición de
un conjunto y sus elementos.
•
Representar la determinación de un
conjunto.
•
Reconocer laclasificacióndelosconjuntos.
Cultivamos valores
•
Educación para la
prevención.
•
Educando para la
gestión de riesgos.
Observa la imagen y contesta.
¿Cómo podemos contribuir a conservar nuestro medio ambiente?
¿Sabes qué otros materiales podemos agrupar y reciclar?

8. INGENIO
8
LABORATORIO
1
1. Formamosequiposdecuatro(4)integrantes.
2. Cada equipo traerá una cartulina y láminas
con imágenes de diversos animales.
1. Cada equipo recortará las imágenes de
los animales.
2. Clasificamos los animales de la siguiente
manera:
• Los animales domésticos.
• Los animales salvajes.
• Los mamíferos.
• Los reptiles.
• Las aves, etc.
3. ¿Se te ocurre alguna otra forma de
clasificar a los animales? Sugiere dos (2)
nuevas formas y discútelas en grupo.
A G R U PAM O S
L O S A N I M A L E S
Nos organizamos
Jugamos y aprendemos
Gana el equipo
que demore
menos en resolver
los ejercicios.

9. INGENIO 9
NOCIÓN DE CONJUNTO
¿Qué es un conjunto?
Es una agrupación de
objetos que presentan
ciertas características
comunes.
En el Parque de las Leyendas de Lima, se ha agrupado a los animales por regiones;
entonces, tenemos la siguiente clasificación:
Conjunto de animales
de la costa
Conjunto de animales
de la sierra
Conjunto de animales
de la selva
CONJUNTOS
Aquí podemos ver
muchos animales
agrupados según
lasregionesdelpaís.
1
TALLER
Hoy visitaremos
el Parque de
las Leyendas.

10. INGENIO
4.° primaria
L U D O M A T I C
10
Todo aquello que forma parte de un conjunto se denomina: elemento.
Ejemplos:
• El pelícano es un elemento del conjunto de animales de la costa.
• El cóndor es un elemento del conjunto de animales de la sierra.
Representación de conjuntos
Los conjuntos se representan de dos formas:
• Entre llaves.
• Figuras geométricas cerradas (diagrama de Venn).
Entre llaves { }
Los conjuntos se denotan con letras mayúsculas: A, B, C,…, P, Q, R,…, Z; de la siguiente
manera:
A = {pelícano; pavo; pato; conejo; paloma}
B = {cóndor; llama; vicuña; puma}
C = {caimán; tortuga; tucán; culebra; mono}
Figuras geométricas cerradas
C
B
A
PERTENENCIA A UN CONJUNTO
Un elemento pertenece a un conjunto cuando forma parte de ese conjunto. Se denota
por el símbolo Î.
A B
El pelícano Î A
El pavo Î A
El conejo Î A
El pato Î A
La paloma Î A
La llama Î B
El cóndor Î B
La vicuña Î B
El puma Î B
Si un elemento no pertenece a un conjunto se denota por el símbolo: Ï.
C
La vicuña Ï C
La llama Ï C
El conejo Ï C

11. INGENIO
L U D O M A T I C
Aritmética
11
ANALIZAMOS Y APRENDEMOS
2
4
3
1. Dados los conjuntos:
A = {1; 2; 3; 4; 5}
B = {2; 4; 6; 8; 10}
Determina el valor de verdad de las
siguientes proposiciones y argumenta
tu respuesta.
a) 2 ∈ B ( ) b) 3 ∉ A ( )
c) 4 ∈ A ( ) d) 5 ∉ B ( )
Resolución:
a)
2 ∈ B es verdadero (V) porque 2 es
un elemento del conjunto B.
b)
3 ∉ A es falso (F) porque 3 es un
elemento del conjunto A.
c)
4 ∈ A es verdadero (V) porque 4 es
un elemento del conjunto A.
d)
5 ∉ B es verdadero (V) porque 5 no
es un elemento del conjunto B.
Dado el siguiente conjunto:
A
Representa el conjunto A mediante
llaves.
Resolución:
a)
Representamos entre llaves, el
conjunto A.
A = {}
; ; ;
Representa el conjunto B mediante llaves
y determina el valor de verdad de las
siguientes proposiciones. Argumenta tu
respuesta.
jueves
viernes
martes
lunes
miércoles
B
I) jueves ∈B ( )
II) sábado ∈ B ( )
III) domingo ∉B ( )
Resolución:
a)
El conjunto B se representa mediante
llaves.
B = {
lunes, martes, miércoles, jueves,
viernes}
b) Analizamos cada caso.
I)
Jueves ∈B es verdadero (V) porque
jueves es un elemento de B.
II)
Sábado ∈ B es falso (F) porque
sábado no es un elemento de B.
III)
Domingo∉Besverdadero(V)porque
domingo no es un elemento de B.
El conjunto B está formado por las
letras de la palabra murciélago.
Representa el conjunto B mediante
llaves y con una figura geométrica
cerrada.
Resolución:
a)
Representamos entre llaves al
conjunto B.
B = {m, u, r, c, i, e, l, a, g, o}
b)
Luego, lo representamos con una
figura geométrica cerrada.
B
m u r c i
e l a g o
1

12. INGENIO
4.° primaria
L U D O M A T I C
12
Indicadores de evaluación
Represento los conjuntos entre llaves y con figuras
geométricas cerradas.
Determino la pertenencia o no pertenencia de
elementos a un conjunto.
Determino la cantidad de elementos de un conjunto.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Se tiene los siguientes conjuntos:
A = {1; 2; 3; 4; 5}; B = {2; 4; 6; 8; 10}
Establece el valor de verdad de
las proposiciones y argumenta tu
respuesta.
I) 5 ∈ A ( )
II) 1 ∉ A ( )
III) 4 ∈ B ( )
IV) 6 ∉ B ( )
Si
8 9
10
7
14
11
13
12
A B
15
16
Determina el valor de verdad de las
siguientes proposiciones. Argumenta
tu respuesta.
I) 11 ∉ A II) 9 ∈ A III) 14∈B
IV) 6 ∈ B V) 6 ∈B
Dados los siguientes conjuntos:
R T S
Relaciona correctamente.
I) ∈ R
II) ∈ T
III) ∈ S
Representa, mediante una figura
geométrica cerrada, el conjunto E y
determina el número de elementos.
E = {}
; ; ;

13. INGENIO 13
FORMAS DE DETERMINAR CONJUNTOS
Por extensión
Se nombra cada uno de los elementos del conjunto.
Ejemplos:
A = {mosca, araña, zancudo, hormiga, cucaracha}
B = {Lunes, martes, miércoles, jueves, viernes, sábado, domingo}
C = {a, e, i, o, u}
Por comprensión
Se nombra la propiedad común de los elementos.
Ejemplos:
A = {
Los insectos} = {x/x es un insecto} y se lee: El conjunto A está constituido por todos los
elementos x tal que x es un insecto.
B =
{Los días de la semana} = {x/x es un día de la semana} y puede leerse también: El
conjunto B está formado por los elementos x que cumplen la condición de ser un
día de la semana.
C =
{Las vocales} = {x/x es una vocal} y se lee: El conjunto C está constituido por los elementos
x tal que x cumple con ser una vocal.
CARDINAL DE UN CONJUNTO
Es la cantidad de elementos diferentes que tiene un conjunto.
Se denota por Card( ) o n( ).
DETERMINACIÓN
DE CONJUNTOS
Asi es; este es
un conjunto
de insectos.
Mira este conjunto que está
formado por una araña; una
mosca; un zancudo; una
hormiga y una cucaracha.
¿Cómosedeterminan
los conjuntos?
Los conjuntos pueden
determinarse de dos
formas:
• Extensión
• Comprensión
B M
a e
i o
u
Card(B) = n(B) = 5 Card(M) = n(M) = 4
Recuerda
Conjunto de los
números naturales
(N)
N = {0; 1; 2; 3; 4; ...}
Importante :
Si un elemento
se repite varias
veces, se cuenta
solo una vez.
2
TALLER

14. INGENIO
4.° primaria
L U D O M A T I C
14
ANALIZAMOS Y APRENDEMOS
1
Representa por comprensión el
conjunto
A = {1; 2; 3; 4; 5}, y comunica tu
respuesta.
Resolución:
a)
El conjunto tiene por elementos a
los números: 1; 2; 3; 4; 5.
Estos son números naturales
mayores que cero y menores que
seis.
Lo representamos como:
0 x 6
b)
Por lo tanto:
A = { x/x ∈ N Ù 0 x 6}
2
Representa por extensión el conjunto.
A = {x/x ∈N Ù 1 £ x 8} y comunica
tu respuesta.
Resolución:
a)
Determinamos las características
del conjunto.
•
x ∈ N
•
1 £ x 8 x = 1; 2; 3; 4; 5; 6; 7
b) Luego, el conjunto B se representa
como:
B = {1; 2; 3; 4; 5; 6; 7}
3 4
Dado el siguiente conjunto:
R = {3; 2; 2; 1}
Determina el Card(R) y argumenta tu
respuesta.
Resolución:
Observamos que, al escribir en el
conjunto R, se repite el elemento 2 y
este debe ser contado una sola vez,
luego Card(R) = 3.
Se tiene el conjunto A = {1; 2; 2; 3; 4}
Determina el Card(A), comunica tu
respuesta.
Resolución:
Tenemos el conjunto:
A = {1; 2; 2; 3; 4}
Observamos que el elemento 2 se
repite dos veces.
Entonces Card(A) = 4.

15. INGENIO
L U D O M A T I C
Aritmética
15
P
∈
P
∈
Indicadores de evaluación
Represento por extensión los conjuntos.
Represento por comprensión los conjuntos.
Determino el cardinal de un conjunto.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Determina por extensión los
siguientes conjuntos, comunicando
tu respuesta.
A = { x/x ∈ N; x £ 6}
B = { x/x ∈ N; 5 £ x 12}
C = { x/x ∈ N; 1 x 10}
D = { x/x ∈ N; 12 x £ 25}
Dados los siguientes conjuntos:
A = { x/x ∈ N; x £ 6}
B = { x/x ∈ N; 5 £ x 25}
Calcula E = n(A) + n(B)argumentando
tu respuesta.
Dados los siguientes conjuntos:
C = {5; 10; 15; 20; 25; 30}
D = {20; 20; 30; 40; 50}
Relaciona correctamente,
argumentando tu respuesta.
I) n(C) a)4
II) n(D) b)6
III) n(C) + n(D) c)10

16. INGENIO
16
CLASES DE CONJUNTOS
¡Mira Alessandra!
Tengo un conjunto
de seis estrellas de
mar de colores.
Álvaro, mi conjunto
es mucho más
grande. Está formado
por toda la arena de
la playa.
CLASES DE CONJUNTOS
Conjunto finito
Es aquel que tiene una cantidad limitada de elementos.
Ejemplo:
A = {las vocales} = {x/x es una vocal} = {a, e, i, o, u}
B = {
los días de la semana} = {x/x es un día de la semana} = {lunes, martes, miércoles,
jueves, viernes, sábado, domingo}
Conjunto infinito
Es aquel que tiene una cantidad ilimitada de elementos.
Ejemplo:
C = {los números naturales} = {x/x es un número natural}
D = {las estrellas del cielo} = {x/x es una estrella del cielo}
TIPOS DE CONJUNTOS
Conjunto vacío o nulo
Es aquel conjunto que no tiene elementos y se denota por:
 o { }
Ejemplo:
E = {los números pares que terminan en tres} = 
F = { x/x ∈ N, x 3 y x 4} = { }
3
TALLER
¿Qué clases
de conjuntos
existen?
Losconjuntosseclasifican
en:
• Finitos.
• Infinitos.

17. INGENIO
L U D O M A T I C
Aritmética
17
Conjunto unitario
Es aquel conjunto que tiene solo un elemento.
Ejemplo:
G = {El presidente actual del Perú}
H = {El satélite natural de la Tierra}
Conjunto universo o universal
Es un conjunto que contiene a todos los conjuntos con los que se desea realizar un
estudio particular.
Ejemplo 1:
A = {aves}
B = {mamíferos}
U = {animales}
U es el universo de A y B.
Simbólicamente, se representa por U y gráficamente
por un rectángulo.
Ejemplo 2:
Sea: V = {varones}
M = {mujeres}
U = {seres humanos}
U es el universo de V y M.
aves
A mam
í
f
e
r
o
s
B
U
animales
V
M
U
seres humanos
A = B
A
El conjunto A es igual al conjunto B.
B = { ; }
Conjuntos iguales
Dos conjuntos son iguales cuando tienen los mismos elementos.
Ejemplo:

18. INGENIO
4.° primaria
L U D O M A T I C
18
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Clasifica los siguientes conjuntos como
unitarios o vacíos.
A = { x/x es el presidente del Perú}
B = { x/x ∈ N Ù 6 x 7}
C = { x/x ∈ N Ù 5 x 7}
Resolución:
Analizamos cada caso.
•
El Perú solo tiene un presidente; por
lo tanto, el conjunto A es unitario.
•
Entre 6 y 7, no hay ningún número
natural; por lo tanto, B es vacío.
•
Entre 5 y 7, existe un único número
natural que es el 6; por lo tanto, es
unitario.
Hernán cobra S/. 2 por cada conjunto
unitario que encuentra.
Si le entregan los siguientes conjuntos:
A = { x/x ∈ N Ù 6 x 8}
B = { x/x ∈ N Ù 5 ≤ x 6}
C = { x/x es una vocal de la palabra mar}
D = {x/x es una vocal de la palabra pozo}
¿Cuál es la mayor cantidad de dinero
que puede recibir? Elabora tu estrategia
de solución.
Resolución:
a) Comprendemos el problema.
Determinamos cuántos de los
conjuntos son unitarios.
b) De los conjuntos:
A = {x/x∈N Ù 6x8} A={7}esunitario
B = { x/x ∈ N Ù 5 ≤ x 6} B = { 5 } es
unitario
C =
{ x/x es una vocal de la palabra mar }
C = { a } es unitario
D =
{ x/x es una vocal de la palabra
pozo} D = { o } es unitario
Por lo tanto, hay 4 conjuntos unitarios.
c) Comunicamos la respuesta.
Hernán cobra 4 × 2 = 8 Nuevos Soles.
Dado el conjunto unitario:
A = { n – 3; m + 3; 8}. Determina n y m,
argumentando tu respuesta.
Resolución:
a)
Sabemos que el conjunto debe
tener solo un elemento, entonces:
n – 3; m + 3 y 8 representan el
mismo elemento.
Entonces: n – 3 = m + 3 = 8
b) De la igualdad, tenemos lo siguiente:
• n – 3 = 8 Þ n = 11
• m + 3 = 8 Þ m = 5
c) Por lo tanto, los valores son
n = 11 y m = 5
Si A = {a – 1; 5}
B = { 3; b}
Son conjuntos iguales. Ahora, determina
a + b. Elabora una estrategia de
solución.
Resolución:
a)
Sabemos que los conjuntos son
iguales; entonces, los elementos son
iguales.
b) a – 1 = 3 ∧ b = 5
a = 4
c) Por lo tanto
a + b = 4 + 5 = 9

19. INGENIO
L U D O M A T I C
Aritmética
19
Indicadores de evaluación
Identifico los conjuntos finitos e infinitos.
Determino los conjuntos vacíos y unitarios.
Clasifico los conjuntos.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Identifica los conjuntos no vacíos.
Comunica tu respuesta.
A = {
x/x es un número impar que
termina en cifra 2}
B = {x/x es una letra del alfabeto}
C = {x/x ∈ N ∧ x 0}
D = {x/x ∈ N ∧ x 0}
En relación a tu medio ambiente,
ejemplifica dos conjuntos infinitos y
dos conjuntos finitos.
Clasifica los siguientes conjuntos
como finitos e infinitos. Comunica tu
respuesta.
P = { x/x es una vocal}
Q = { x/x es una estrella}
R = { x/x es un número par}
S =
{ x/x es un número natural de 2
cifras}
Dado el conjunto unitario:
P = { a + 2; b – 2; 3}
Determinaloselementosdelconjunto
finito.
Q = {x/x ∈ N ∧ a x b}

20. PROYECTO DE APRENDIZAJE N.0 1
INGENIO
1. Situación problemática
El reciclaje consiste en aprovechar y transformar los materiales u objetos que han sido
utilizados con la finalidad de reincorporarlos como materia prima para la fabricación
de nuevos productos. El problema actual que atravesamos respecto al reciclaje es la
falta de conciencia, información e interés de la comunidad para darle un mejor destino
a estos residuos que, poco a poco, están acabando con el medio ambiente. Por esta
razón, es importante que nuestros estudiantes aprendan la importancia de reciclar.
2. Finalidad
•
Emplear los conjuntos en la clasificación de los distintos tipos de residuos en
envases de colores.
•
Reconocer la importancia de los conjuntos y su utilidad en situaciones
problemáticas de nuestro entorno.
3. Recursos materiales
Depósitos de basura. Hojas bond.
Bolsas de basura de color azul, amarillo y verde. Cinta adhesiva.
Lápices y plumones. Regla y goma.
Papel lustre de color azul, amarillo y verde.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
5. Evaluación
CONJUNTOS
1.ª etapa 2.ª etapa 3.ª etapa
Organícense en grupos de 4 estudiantes.
Identifiquen los lugares más adecuados
para ubicar los envases para reciclar.

Forren los envases con el papel lustre de
color e identifíquenlo.
• Azul (papel y cartón)
• Verde (vidrio)
• Amarillo (plástico y latas)
Elaborenafichesyvolantesdondesedivulga
la necesidad de clasificar los desechos.
Pegan los afiches
y se reparte los
volantes.
Ubican los depósitos
en los lugares
adecuados.
Elaboran un informe
deltrabajorealizado
y lo sustentan.
Haz un informe
para ver si se
ha logrado el
objetivo.
20

21. Educación en prevención
SISTEMA DE
NUMERACIÓN
Aprendemos a:
•
Representar números naturales en la
recta numérica.
•
Descomponer números naturales por
el valor de las cifras y por notación
desarrollada.
•
Comparar números naturales.
• Aproximar números a la decena,centena
y millar más cercano.
Cultivamos valores
•
Educación para
gestión de riesgos.
• Responsabilidad.
Observa la imagen y contesta.
¿Consideras importante los simulacros de sismo?
¿En tu colegio realizan habitualmente simulacros de sismo?
UNIDAD
2

22. INGENIO
22
2
LABORATORIO
1)
Vamos a trabajar con las siguientes cifras: 5;
1 y 9.
2)
Escribimos estos números en las figuras
recortadas.
3)
Ordenamos las figuras, formando números de
menor a mayor.
4)
Luego, reordenamos las figuras, esta vez de
mayor a menor.
Seguimos jugando. Luego, cada grupo
resolverá las siguientes preguntas:
a)
Identificamos el menor número formado
con estas 3 cifras.
b)
Reconocemos el mayor número formado
con estas 3 cifras.
c) ¿
Cuál es el resultado de sumar el mayor con
el menor número formado?
d) ¿
Cuál es el resultado de restar el mayor con
el menor número formado?
e)
Al ordenar los números de mayor a menor,
¿qué número ocupa la tercera ubicación?
f)
Gana el primer grupo que presente los
resultados correctos.
Fig. 1
J U G AM O S C O N
L O S N Ú M E R O S
Nos organizamos
1) Formamos grupos de cuatro (4) integrantes.
2)
Cada grupo recorta 6 figuras: dos estrellas, dos
rectángulos, dos círculos (fig. 1).
LABORATORIO
2
Jugamos y aprendemos

23. INGENIO 23
DISTRITO NIÑOS
San Juan de Lurigancho 219 529
San Martín de Porres 135 506
Ate Vitarte 124 921
Villa El Salvador 103 089
Villa María del Triunfo 98 857
10 unidades (U)
10 decenas (D)
10 centenas (C)
Equivalen a
Equivalen a
Equivalen a
1 decena (D)
1 centena (C)
1 unidad de millar (UM)
SISTEMA DE NUMERACIÓN DECIMAL
Las cifras usadas en el sistema de numeración son 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Con ellas,
podemos escribir cualquier número por muy grande que sea.
SISTEMA DE
NUMERACIÓN DECIMAL
¡Increíble! la mayor
cantidad de niños
viven en el distrito
de San Juan de
Lurigancho.
Lucero, ¿en qué
distrito de Lima
vive la mayor
cantidad de
niños?
¿Qué sistema
de numeración
usamos?
Usamos el sistema de
numeración decimal en
donde las unidades se
agrupan de 10 en 10.
4
TALLER

24. INGENIO
4.° primaria
L U D O M A T I C
24
REPRESENTACIÓN GRÁFICA DE UN NÚMERO
De nuestro ejemplo, el número de niños de San Juan de Lurigancho se puede representar
como:
a) Tablero de Valor Posicional
CM DM UM C D U
2 1 9 5 2 9
b) Ábaco
UM
DM
CM C D U
c) En la recta numérica
218 000
217 000
216 000
215 000 220 000
219 529
LECTURA DE NÚMEROS
Sean los números:
CM DM UM C D U
2 1 9 5 2 9
Se lee doscientos diecinueve mil quinientos veintinueve.
Ejemplo:
Completamos las diferentes representaciones del número 135 413.
a) Ábaco
UM
DM
CM C D U
b) Tablero de Valor Posicional
CM DM UM C D U
1 3 5 4 1 3
c) En la recta numérica
135 200 135 300 135 400 135 500 135 600
135 100
135 000
135 413
Se lee ciento treinta y cinco mil cuatrocientos trece.

25. INGENIO
L U D O M A T I C
Aritmética
25
Si un mismo número se representa de
dos maneras diferentes:
CM DM UM C D U
4 6
Ubica el número en la recta numérica.
Resolución:
a) Completamos el cuadro.
CM DM UM C D U
3 4 6 1 6 4
b)
Ubicamos en la recta numérica.
346 000 346 100 346 200

346 164
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Ubica los números en la recta de los
números naturales.
CM DM UM C D U
4 2 8 3 4 1
6 1 7 4 5 2
Resolución:
a)
Ubicamos los números en la recta
de los números naturales.
425 000
615 000
426 000
616 000
427 000
617 000
428 000
618 000
429 000
619 000
428 341
617 452


Completa el cuadro:
Resolución:
a) Completamos el cuadro.
CM DM UM C D U
Dieciséis mil noventa
y dos
1 6 0 9 2
Veintitrés mil
cuatrocientos veintitrés
2 3 4 2 3
Ciento ochenta y cinco
mil ochocientos cuatro
1 8 5 8 0 4
CM DM UM C D U
Dieciséis mil noventa
y dos
Veintitrés mil
cuatrocientos veintitrés
Ciento ochenta y cinco
mil ochocientos cuatro
Se tiene dos números. Representa
dichos números en el Tablero de Valor
Posicional y ábaco respectivamente.
Resolución:
UM
DM
CM C D U
CM DM UM C D U
1 2 5 2 6 4
a)
UM
DM
CM C D U
CM DM UM C D U
8 2 3 5 4 2
b)
CM DM UM C D U
8 2 3 5 4 2
a) b)
UM
DM
CM C D U

26. INGENIO
4.° primaria
L U D O M A T I C
26
Ubica las cifras en la recta de los
números naturales.
•
Doscientos cuatro mil trescientos
cincuenta y tres.
•
Trescientos siete mil cuarenta y dos.
•
Quinientos tres mil seiscientos
quince.
Ubica las cifras en la recta de los
números naturales.
•
Doscientos cuatro mil trescientos
cincuenta y tres.
•
Trescientos siete mil cuarenta y dos.
•
Quinientos tres mil seiscientos
quince.
Relaciona los números con su lectura
correspondiente.
Relaciona los números con su lectura
correspondiente.
Indicadores de evaluación
Identifico números hasta 999 999.
Represento números hasta 999 999.
Ubico números hasta 999 999 en la recta numérica.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
200 542
Ciento cuarenta y cuatro
mil treinta y dos.
Ochenta y dos mil
setecientos diecisiete.
Doscientos mil quinientos
cuarenta y dos.
144 032
82 717
Ubica en el Tablero de Valor
Posicional los siguientes números:
• 432 001
• 184 203
•
Ciento cuatro mil trescientos
cuarenta y tres.
•
Diecinueve mil doscientos
cincuenta y siete.
Completa el cuadro.
Representación CM DM UM C D U
UM
DM
CM C D U
UM
DM
CM C D U

27. INGENIO 27
DESCOMPOSICIÓN,
COMPARACIÓN Y
APROXIMACIÓN DE N
FORMAS DE DESCOMPOSICIÓN DE UN NÚMERO
1) Por el valor de sus cifras, tenemos los siguientes ejemplos:
S/. 1 426
Es decir, 1UM + 4C + 2D + 6U. Es decir, 2UM + 1C + 3D + 7U.
Es decir, 1CM + 2DM + 4UM + 4C + 2D + 6U.
1 426 = 2 137 =
124 426 =
UM C D U
1 4 2 6
UM C D U
2 1 3 7
CM DM UM C D U
1 2 4 4 2 6
Claro, la podemos
comprar si papá da
S/. 1 000, nuestro
hermano mayor S/. 400,
tú S/. 20 y yo S/. 6.
Mira, Lucero, ¡que
bonita cocina!
Deberíamos
comprarla para
mamá.
De 2 formas:
• Por el valor de sus cifras.
•
Por notación
desarrollada.
¿De cuántas formas
podemos descomponer
un número?
2) Notación desarrollada.
1 426 = 1UM + 4C + 2D + 6U 2 137 = 2UM + 1C + 3D + 7U
= 1 000 + 400 + 20 + 6 = 2 000 + 100 + 30 + 7
5
TALLER

28. INGENIO
4.° primaria
L U D O M A T I C
28
Margarita elegirá la cotización de S/. 233 569.
COMPARACIÓN DE NÚMEROS NATURALES
Para comparar dos números, usamos los símbolos:
APROXIMACIONES A LA DECENA, CENTENA O MILLAR MÁS CERCANO
Para aproximar un número a la decena, centena o unidad de millar, debemos observar la
cifra ubicada en la posición anterior. Si la cifra es menor que 5, aproximamos a la decena,
centena o unidad de millar inferior. Si es mayor o igual a 5, aproximamos a la decena, centena
o unidad de millar superior.
Ejemplo:
Si Margarita desea comprar una casa y tiene las cotizaciones S/. 233 887 y S/. 233 569,
¿cuál de ellas elegirá si desea la más económica?
De nuestro ejemplo:
• Iniciamos la comparación.
124 426 = 1 CM + 2DM + 4UM + 4C + 2D + 6U
= 100 000 + 20 000 + 4 000 + 400 + 20 + 6
Del otro ejemplo:
=
=
=
CM DM UM C D U
2 3 3 8 8 7
CM DM UM C D U
2 3 3 5 6 9
(2 = 2)
(3 = 3)
(3 = 3)
(8 5)
se lee menor que
se lee mayor que
= se lee igual que
Observación
Cuandocomparamosdosnúmeros,
se empieza a comparar por la cifra
de mayor orden hasta encontrar la
desigualdad.
Ejemplo 1:
Álvaro recorre 2 674 kilómetros,
¿a qué unidad de millar está más
próximo su recorrido? 2 000 km 2 500 3 000 km
Ejemplo 3:
• Aproximamos a la decena más
próxima. 2 670 2 675 2 680 km
Observamos la cifra de la posición anterior (la unidad): como es 4, o sea menor que 5,
aproximamos a la decena inferior. Entonces, Álvaro recorrió aproximadamente 2 670 km.
• Observamos la cifra de la posición anterior (la centena): como es 6, o sea mayor que 5,
aproximamos a la unidad de millar superior. Entonces, Álvaro recorrió aproximadamente
3 000 km.
Ejemplo 2:
• Aproximamos a la centena
más próxima. 2 600 km 2 650 2 700 km
Observamos la cifra de la posición anterior (la decena): como es 7, o sea mayor que 5,
aproximamos a la centena superior. Entonces, Álvaro recorrió aproximadamente 2 700 km.

29. INGENIO
L U D O M A T I C
Aritmética
29
3 4
ANALIZAMOS Y APRENDEMOS
1. Relaciona los números con su notación
desarrollada. Argumenta tu respuesta.
323 472
101 351
257 896
100 000 + 1 000 + 300 + 50 + 1
200 000 + 50 000 + 7 000 + 800 + 90 + 6
300 000 + 20 000 + 3 000 + 400 + 70 + 2
Resolución:
a)
Efectuamos la notación desarrollada
de cada número:
b) Entonces:
CM DM UM C D U
| 2 3 4 7 2 300000+20000+3000+400+70+2
1 0 1 3 5 1 100 000 + 1 000 + 300 + 50 +1
2 5 7 8 9 6 200000+50000+7000+800+90+6
323 472
101 351
257 896
100 000 + 1 000 + 300 + 50 + 1
200 000 + 50 000 + 7 000 + 800 + 90 + 6
300 000 + 20 000 + 3 000 + 400 + 70 + 2
2. Completa la tabla.
UM C D U
6 000 + 400 + 30 + 4
3 Um + 7C + 4D + 8U
9 + 50 + 700 + 2 000
Resolución:
a)
Determinamos los números a partir
de la notación desarrollada y del
orden de las cifras.
6 000 + 400 + 30 + 4 = 6 434
3 Um + 7C + 4D + 8U = 3 748
9 + 50 + 700 + 2 000 = 2 759
b)
Entonces, la tabla se completa de
la siguiente manera:
UM C D U
6 000 + 400 + 30 + 4 6 4 3 4
3 Um + 7C + 4D + 8U 3 7 4 8
9 + 50 + 700 + 2 000 2 7 5 9
1 2
Si se tiene las cifras 6; 7; 2; 1; 4 y 8, ¿cuál
es el mayor número que se puede
formar? Comunica tu respuesta.
Resolución:
a)
Tenemos las cifras 6; 7; 2; 1; 4 y 8.
b)
Ordenamos los números de mayor
a menor orden en el tablero
posicional.
CM DM UM C D U
8 7 6 4 2 1
c)
Por lo tanto, el número mayor que
se puede formar es 876 421.
Realiza las aproximaciones de los
siguientes números:
a) 3 527 a las decenas.
b) 215 892 a las unidades de millar.
Resolución:
a)
Realizamos la aproximación a
las decenas.
UM C D U
3 5 2 7
3 527 está entre 3 520 y 3 530.
La aproximación será a 3 530
porque está más cerca.
b)
Realizamos la aproximación a
las unidades de millar.
CM DM UM C D U
2 1 5 8 9 2
215 892 está entre 215 000 y 216 000.
La aproximación será a 216 000
porque está más cerca.

30. INGENIO
4.° primaria
L U D O M A T I C
30
Relaciona los números con su
descomposición por el orden de sus
cifras.
Relaciona los números con su
descomposición por el orden de sus
cifras.
2.Determina el valor de verdad de las
siguientes proposiciones.
a)
b)
c) +
2.Determina el valor de verdad de las
siguientes proposiciones.
a)
b)
c) +
3. Aproxima los números a la decena
de millar. Marca tu respuesta.
3. Aproxima los números a la decena
de millar. Marca tu respuesta.
Indicadores de evaluación
Aprendo a descomponer números de hasta 6 cifras.
Comparo números de hasta 6 cifras.
Aproximo números de hasta 6 cifras.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
217 583 300 000 + 20 000 + 3 000 + 700 + 20 + 1
323 721 1CM + 4DM + 2UM + 8C + 9D +8U
142 898 2CM + 1CM + 7UM + 5C + 8D +3U

31. 1. Situación problemática
Hoy en día, los medios de comunicación cumplen una función muy importante al
informarnos sobre lo que ocurre en nuestro país y el mundo.
En las noticias del periódico, la televisión y la radio escuchamos y vemos datos
estadísticos sobre la cantidad de habitantes que hay en un país, datos sobre su
economía e información sobre los presupuestos de las grandes obras de ingeniería para
la ciudad, entre otras cosas. Todas estas informaciones, muchas veces, las representan
con números grandes que debemos aprender a leer y representar.
2. Finalidad
•
Representar cantidades grandes, como el presupuesto de una obra, en el Tablero
de Valor Posicional y su notación desarrollada.
•
Reconocer la importancia de la representación de los números.
3. Recursos materiales
Revistas y periódicos. Goma y tijera. Papelotes.
Cinta adhesiva. Plumones.
4. Etapas y actividades
PROYECTO DE APRENDIZAJE N.0
2
INGENIO
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1.ª etapa 2.ª etapa
Busquen en sus revistas o
periódicos, información que
empleen números hasta 999
999, recórtenlas y péguenlas
en su papelote.
Las cantidades escritas en el papelote deben
ser representadas en el Tablero de Valor
Posicional y con su notación desarrollada.
Comparan los números y determinar su orden.

Exponensutrabajo,explicandolarepresentación
que le resultó más sencilla de usar y cómo
ordenaron los números.
SISTEMA DE NUMERACIÓN
31

32. UNIDAD
3
Vivir en paz
NÚMEROS
NATURALES
Cultivamos valores
•
Educación para la
paz.
•
Tolerancia.
Aprendemos a:
• Resolverproblemasdeadiciónysustracción
de números naturales.
•
Interpretar y formular sucesiones con
números naturales.
Observa la imagen y contesta.
¿Qué entiendes por vivir en paz?
¿Porqué crees que es importante vivir en paz y armonía?

33. INGENIO 33
LABORATORIO
3
1.
Con lápiz, coloca las letras a, b, c …
en el orden que se muestra. (Ver fig. 2).
2. Pintan los cuadrados a; e y h de color
amarillo.
3. En los cuadrados pintados, escribe
con plumón los siguientes números:
4 en a; 5 en e; 1 en h
4. Completan los otros cuadrados con
números del 1 al 9, diferentes a los
que ya fueron colocados.
5. La condición es que la suma
horizontal, vertical y diagonal sea
15. (Ver fig. 3)
fig. 1
fig. 2
fig. 3
a b c
d e f
g h i
4
5
1
15
15
15
15
15
15
J U G AM O S y
A P R E N D E M O S
Nos organizamos
1. Formamos grupos de cuatro (4) integrantes.
2. En una cartulina, dibujamos dos cuadrados.
(Ver fig. 1)
Jugamos y aprendemos
Gana el
equipo que
termine
primero.

34. INGENIO
34
TALLER
ADICIÓN EN 
6
¿Cómo lo
resolvemos?
De nuestro ejemplo:
Para calcular la producción total de la semana, sumamos 212 352 y 110 126.
UM
DM
CM C D U
UM
DM
CM C D U UM
DM
CM C D U
CM DM UM C D U
2 1 2 3 5 2
1 1 0 1 2 6
3 2 2 4 7 8 Suma
Sumandos
+
Este mes la fábrica
“Todo se puede”,
ha confeccionado
212 352 pantalones.
Asi es, pero además
ha confeccionado
110 126 casacas.
¿Cuántas prendas ha
confeccionado en
total?
Observación
Los términos de la adición
son los sumandos y la
suma.
La adición, que es una
operación de números
naturales, la cual permite
juntar, agrupar, aumentar,
etc. y al resultado se lo
denomina suma.
a + b = S
ADICIÓN Y
SUSTRACCIÓN EN N

35. INGENIO
L U D O M A T I C
Aritmética
35
SUSTRACCIÓN
Es la operación que consiste en disminuir a una cantidad llamada minuendo (M), otra
cantidad menor llamada sustraendo (S), obteniéndose un resultado que llamaremos
diferencia (D).
Ejemplo:
Si Lucero tiene ahorrado S/. 101 735, ¿cuánto de dinero le falta para comprar la casa?
El orden de los
s u m a n d o s n o
altera el resultado.
Si se agrupa
los sumandos
de diferente
manera, no
se modifica el
resultado final.
La suma de un número
con cero (0) da como
resultado el mismo
número.
Propiedad
conmutativa
Propiedad
asociativa
Propiedad del
elemento neutro
b) 132 352 + 241 126 = 241 126 + 132 352
c) Si agrupamos
d) Calcular
475 620 + 0 = 475 620
Elemento neutro
de la adición.
373 478 373 478
(125 423 + 124 138) + 642 315
249 561 + 642 315
125 423 + (124 138 + 642 315)
125 423 + 766 453
=
891 876 891 876
=
=
=
Restamos verticalmente
A Lucero le falta S/. 140 825 para comprar la casa.
Comprobación
En toda sustracción, se cumple que:
Sustraendo + Diferencia = Minuendo
Minuendo
Minuendo
Sustraendo
Sustraendo
Diferencia
Diferencia
–
+
Propiedades de la adición
a) Sabemos que:
• 212 352 es un número natural
• 110 126 es un número natural
• 322 478 es un número natural
La suma de dos números
naturales da como resultado
otro número natural.
Propiedad
de clausura
CM DM UM C D U
2 4 2 5 6 0
1 0 1 7 3 5
1 4 0 8 2 5
CM DM UM C D U
1 0 1 7 3 5
1 4 0 8 2 5
2 4 2 5 6 0
S/. 242 560
Observación
Los términos de la sustracción son
los siguientes:
• Minuendo.
• Sustraendo.
• Diferencia.
M – S = D
Sustraendo + Diferencia + Minuendo = 2(Minuendo)

36. INGENIO
4.° primaria
L U D O M A T I C
36
Determina el resultado de sumar las
cantidades mostradas. Comunica tu
respuesta.
+
Resolución:
a)
Representamos en el Tablero de Valor
Posicional la cantidad que está en el
ábaco.
UM
DM
CM C D U
+
b) Efectuamos la suma.
Por lo tanto, el resultado de la suma
Determina el resultado de sumar las
cantidades mostradas. Comunica tu
respuesta.
+
Resolución:
a)
Representamos en el Tablero de Valor
Posicional la cantidad que está en el
ábaco.
UM
DM
CM C D U
+
b) Efectuamos la suma.
Por lo tanto, el resultado de la suma
2. Analiza y escribe las propiedades
aplicadas.
a) 124 123 + = 124 123
b) 181 230 + 151 260 = 151 260 + 181 230
c) (127 123 + 10 141) + 7 831 = 127 123 +
(10 141 + 7 831)
Resolución:
124 123 + 0 = 24 123: propiedad del
elemento neutro, pues el sumando
no se modifica.
b) Propiedad conmutativa: el orden
de los sumandos no altera la suma.
c) Propiedad asociativa: si agrupamos
de diferente manera los sumandos,
la suma no se altera.
2. Analiza y escribe las propiedades
aplicadas.
a) 124 123 + = 124 123
b) 181 230 + 151 260 = 151 260 + 181 230
c) (127 123 + 10 141) + 7 831 = 127 123 +
(10 141 + 7 831)
Resolución:
124 123 + 0 = 24 123: propiedad del
elemento neutro, pues el sumando
no se modifica.
b) Propiedad conmutativa: el orden
de los sumandos no altera la suma.
c) Propiedad asociativa: si agrupamos
de diferente manera los sumandos,
la suma no se altera.
3. Una empresa compra un edificio en
S/. 475 560 y un terreno valorizado en
S/. 245 300. Si después de realizada la
compra, queda en la empresa S/. 240 000,
¿cuánto dinero tenía la empresa?
Resolución:
a) Comprendemos el problema.
Costos de la compra:
• Edificio = S/. 475 640
• Terreno = S/. 245 300
• Dinero que queda = S/. 240 000
b) Sumamos:
475 640 +
245 300
240 000
960 940
c) Comunicamos la respuesta.
La empresa tenía S/. 960 940.
3. Una empresa compra un edificio en
S/. 475 560 y un terreno valorizado en
S/. 245 300. Si después de realizada la
compra, queda en la empresa S/. 240 000,
¿cuánto dinero tenía la empresa?
Resolución:
a) Comprendemos el problema.
Costos de la compra:
• Edificio = S/. 475 640
• Terreno = S/. 245 300
• Dinero que queda = S/. 240 000
b) Sumamos:
475 640 +
245 300
240 000
960 940
c) Comunicamos la respuesta.
La empresa tenía S/. 960 940.
4.
Enelaño2000,eldistritodeComastenía
345 600 habitantes y en la actualidad,
2 015, hay 400 000 habitantes. ¿En
cuántos habitantes aumentó la
población?
Resolución:
a)Comprendemos el problema.
El aumento de la población es la
diferencia entre los habitantes que
hay y los que habían.
Ejecutamos la operación.
400 000 –
345 600
54 400
Comunicamos la respuesta.
La población aumentó en 54 400
habitantes.
4.
Enelaño2000,eldistritodeComastenía
345 600 habitantes y en la actualidad,
2 015, hay 400 000 habitantes. ¿En
cuántos habitantes aumentó la
población?
Resolución:
a)Comprendemos el problema.
El aumento de la población es la
diferencia entre los habitantes que
hay y los que habían.
Ejecutamos la operación.
400 000 –
345 600
54 400
Comunicamos la respuesta.
La población aumentó en 54 400
habitantes.
1 2
3 4
ANALIZAMOS Y APRENDEMOS

37. INGENIO
L U D O M A T I C
Aritmética
37
Resuelve los espacios en blanco.
Resuelve los espacios en blanco. Relaciona cada columna con la
proposición que le corresponde.
I)
a)
b)
c)
II)
III)
Relaciona cada columna con la
proposición que le corresponde.
I)
a)
b)
c)
II)
III)
Comprende y resuelve.
Mi papá tenía ahorrado S/. 542 400
en el banco. Si retira S/. 345 600 para
comprar una casa y luego deposita
S/. 42 600, ¿cuánto dinero tiene ahora
en el banco?
Comprende y resuelve.
Mi papá tenía ahorrado S/. 542 400
en el banco. Si retira S/. 345 600 para
comprar una casa y luego deposita
S/. 42 600, ¿cuánto dinero tiene ahora
en el banco?
Comprende y resuelve.
La I. E. “Los Niños de Jesús” realizó
un bingo, obteniendo S/. 112 120
en ingresos. Si los gastos fueron de
S/. 41 230, ¿cuál fue el monto de la
ganancia?
Comprende y resuelve.
La I. E. “Los Niños de Jesús” realizó
un bingo, obteniendo S/. 112 120
en ingresos. Si los gastos fueron de
S/. 41 230, ¿cuál fue el monto de la
ganancia?
Indicadores de evaluación
Reconozco las propiedades de la adición.
Interpreto la adición y sustracción de números
naturales.
Resuelvo problemas de la vida diaria, usando las
operaciones de adición y sustracción.
AUTOEVALUACIÓN
CM DM UM C D U
7 4 1 4 3 2
1 5 9
6 7 9 6
+
a)
b)
–
CM DM UM C D U
4 6 3 0
2 3 5
4 2 4 4
PIENSO Y RESUELVO
1
3
2
4

38. INGENIO
38
De nuestro ejemplo, luego de 5 días tendrá lo siguiente:
Luego, esta sucesión se puede escribir:
+ 2 +2 + 2 + 2
1.er
término (a1
)
Razón
1 ; 3 ; 5 ; 7 ; 9…
SUCESIÓN DE NÚMEROS NATURALES
1 figurita 3 figuritas
+ 2 stickers + 2 stickers + 2 stickers + 2 stickers
5 figuritas 7 figuritas 9 figuritas
1.er
día
Lunes
2.o
día
Martes
3.er
día
Miércoles
4.o
día
Jueves
5.o
día
Viernes
SUCESIONES CON
NÚMEROS NATURALES
Sí, empezaré a
completarlo pegando
1 figurita el día lunes y
cada día le aumentaré
2 figuritas más.
¡Hola,
Álvaro! ¿Te
compraste
un nuevo
álbum?
La sucesión cumple con la regla de formación;
“sumar 2”; por lo tanto, hasta el día viernes, Álvaro
habrá pegado 9 figuritas.
Ejemplo:
Encuentra el número que sigue 100 202; 100 205;
100 208.
En esta sucesión, se tiene el dato:
Primer término (a1
) = 100 202
Regla de formación: sumar 3
El número que sigue es 100 208 + 3 = 100 211
Observación
La razón se obtiene restando
dos términos consecutivos de
una sucesión.
¿En qué consiste una
sucesión numérica?
Es un arreglo de números
naturales que sigue una
determinada Ley de
Formación.
TALLER
7

39. INGENIO
L U D O M A T I C
Aritmética
39
Se tiene la siguiente información:
• El primer término es 4.
• La razón es 5.
Determina el séptimo término de la
sucesión. Argumenta tu respuesta.
Resolución:
a) Sabemos que: a1
= 4; razón = 5
b)
Formamos la sucesión, sumando 5 a
partir del primer término.
4 ; 9 ; 14 ; 19 ; 24 ; 29 ; 34
Luego:
4; 9; 14; 19; 24; 29; 34
1º 2º 3º 4º 5º 6º 7º
d)
Por lo tanto, el séptimo término de
la sucesión es 34.
Se tiene la siguiente información:
• El primer término es 4.
• La razón es 5.
Determina el séptimo término de la
sucesión. Argumenta tu respuesta.
Resolución:
a) Sabemos que: a1
= 4; razón = 5
b)
Formamos la sucesión, sumando 5 a
partir del primer término.
4 ; 9 ; 14 ; 19 ; 24 ; 29 ; 34
Luego:
4; 9; 14; 19; 24; 29; 34
1º 2º 3º 4º 5º 6º 7º
d)
Por lo tanto, el séptimo término de
la sucesión es 34.
2. Dada la siguiente sucesión:
1; 7; 13; 19; 25; …; 43
Relaciona correctamente las columnas,
argumentando tu respuesta.
Resolución:
a) Completamos los términos de la
sucesión, sabiendo que la razón es 6.
1; 7; 13; 19; 25; 31; 37; 43
b)
Relacionando las columnas:
2. Dada la siguiente sucesión:
1; 7; 13; 19; 25; …; 43
Relaciona correctamente las columnas,
argumentando tu respuesta.
Resolución:
a) Completamos los términos de la
sucesión, sabiendo que la razón es 6.
1; 7; 13; 19; 25; 31; 37; 43
b)
Relacionando las columnas:
Dada la sucesión: 2; 5; 8; … ; 23,
establece el valor de verdad de las
siguientes proposiciones.
Argumenta tu respuesta.
I) El primer término es 1. ( )
II) La razón de la sucesión es 3. ( )
III) El término 7 es 23. ( )
Resolución:
a)
Identificamos los términos de una
sucesión:
2; 5; 8; … ; 23
El primer término es 2.
La razón es 3.
b)
Completamos los términos
I) Falso, porque el 1.er
término es 2.
II)
Verdadero, porque los términos
aumentan de 3 en 3.
III) Falso, porque el sétimo término es 20.
Dada la sucesión: 2; 5; 8; … ; 23,
establece el valor de verdad de las
siguientes proposiciones.
Argumenta tu respuesta.
I) El primer término es 1. ( )
II) La razón de la sucesión es 3. ( )
III) El término 7 es 23. ( )
Resolución:
a)
Identificamos los términos de una
sucesión:
2; 5; 8; … ; 23
El primer término es 2.
La razón es 3.
b)
Completamos los términos
I) Falso, porque el 1.er
término es 2.
II)
Verdadero, porque los términos
aumentan de 3 en 3.
III) Falso, porque el sétimo término es 20.
En una vereda, Piero salta de loseta
en loseta, dejando un espacio entre
ellos. Si luego de 7 saltos llega a su casa,
¿cuántas losetas tiene esa vereda?
Resolución:
a) Graficamos y numeramos los
recuadros donde pisa el niño. Luego,
los sombreamos.
b)
Expresamos numéricamente lo
siguiente:
c)
Comunicamos la respuesta. Hay un
total de 13 losetas en la vereda.
En una vereda, Piero salta de loseta
en loseta, dejando un espacio entre
ellos. Si luego de 7 saltos llega a su casa,
¿cuántas losetas tiene esa vereda?
Resolución:
a) Graficamos y numeramos los
recuadros donde pisa el niño. Luego,
los sombreamos.
b)
Expresamos numéricamente lo
siguiente:
c)
Comunicamos la respuesta. Hay un
total de 13 losetas en la vereda.
1 2
3 4
ANALIZAMOS Y APRENDEMOS
La sucesión tiene 6
37
8 términos
La razón de la sucesión es
El sétimo término es

40. INGENIO
4.° primaria
L U D O M A T I C
40
Indicadores de evaluación
Establezco el criterio de referencia de una sucesión.
Establezco los términos de una sucesión.
Resuelvo problemas haciendo uso del criterio de
sucesión.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4 Álvaro salta en una vereda de dos
losetas en dos losetas. Si luego de seis
saltos, llega a la tienda, ¿cuántas
losetas tiene esa vereda?
Dada la siguiente sucesión:
2; 7; 12; 17; 22; 27; 32.
Relaciona correctamente.
Razón 7
5
2
Primer término
Total de términos
Se tiene la siguiente sucesión de
cubos; determina cuántos cubos
habrá en la 4.a
posición.
; …
;
;

41. PROYECTO DE APRENDIZAJE N.0
3
INGENIO
1.ª etapa 2.ª etapa
Forman grupos de cuatro (4)
estudiantes.

Elaboran una lista con la
cantidad de alimentos y
productos necesarios en un
mes.
Identifican en la revista los
precios de los productos
seleccionados.
Eligen un monto de dinero con el que
supuestamente contaríamos, tomando como
referencia el sueldo de nuestros padres.

Determinan el costo de cada uno de los
productos y la suma de los mismos.

Calculan la diferencia entre el sueldo y los
gastos que ocurririan. Luego, exponen el
resultado de su trabajo.
NÚMEROS NATURALES
1. Situación problemática
Establecer un presupuesto es necesario cuando se pretende realizar una compra,
una inversión, una refacción, etc. Esto nos permite conocer los ingresos y gastos que
realizaremos para llevar a cabo dicha acción; también, nos permite organizarnos
y programar convenientemente cuándo ejecutaremos nuestros planes. Por ello, es
necesario conocer las operaciones básicas de adición y sustracción.
2. Finalidad
Que los estudiantes utilicen las operaciones básicas de adición y sustracción al
momento de elaborar un presupuesto.
3. Recursos materiales
Revistas de supermercados. Hojas bond. Goma y tijera.
Lápices y plumones. Regla.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
41

42. Convivir en igualdad y respeto
Cultivamos valores
•
Educación para la
convivencia, la paz
y la ciudadanía.
•
Educación para la
paz.
Observa la imagen y contesta.
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es muy importante en tu familia?
UNIDAD
4
OPERACIONES
CON NÚMEROS
NATURALES
Aprendemos a
•
Resolver ejercicios y problemas con
multiplicación de números naturales.
•
Representar y resolver problemas con
proporcionalidad.
•
Resolver ejercicios y problemas con
división de números naturales.

43. INGENIO 43
1. Formanequiposdecuatro(4)integrantes.
2.
Cada grupo debe contar un con
lápiz, papel y una cartulina.
4
LABORATORIO
A R M AM O S U N
R O M P E C A B E Z A S
Nos organizamos
Jugamos y aprendemos
3. El profesor entregará una hoja
con unos gráficos en una cara y
operaciones matemáticas en la otra.
4. Las operaciones son las siguientes:
a. (100 + 13) × (100 – 2)
b. (30 – 3) × 32
c. (80 + 5) × (80 + 14)
d. (100 + 22) × (100 – 60)
5. Identifican el menor número
obtenido con estas operaciones.
6. Identifican el mayor número
obtenido con estas operaciones.
7. Ordenan de menor a mayor los
resultados obtenidos.
8. Cortan las figuras por las
líneas punteadas y arman el
rompecabezas, ordenando
las figuras de menor a mayor y
pegándolo en la cartulina.
9. Ganan el equipo que termine
primero.
c
b
d
a

44. INGENIO
44
MULTIPLICACIÓN DE
NÚMEROS NATURALES
TALLER
8
Así es, observa
que hay 5 grupos.
¿Cuántas botellas
de yogur habrán?
¡Mira! Las botellas
de yogur están
agrupadas
de 4 en 4.
MULTIPLICACIÓN
PROPIEDADES DE LA MULTIPLICACIÓN
51 234
102 468
2
PROPIEDAD DE CLAUSURA
La multiplicación de dos números naturales da
como producto otro número natural.
CM DM UM C D U
5 1 2 3 4
2
1 0 2 4 6 8
De nuestro ejemplo:
= 4 + 4 + 4 + 4 + 4 = 4 × 5 = 20 producto
5 veces también se les llama factores
12 × 13 = 156
Multiplicador
Multiplicando
Producto
Hay 20 botellas de yogur.
Si:
Es una suma abreviada, en
donde un número llamado
multiplicando se suma tantas
veces como lo indica otro
número llamado multiplicador.
Al resultado se lo llama
producto.
¿Qué es la
multiplicación?

45. INGENIO
L U D O M A T I C
Aritmética
45
• Se tiene la siguiente distribución de manzanas.
4
filas
5 columnas
En una fila hay 5 , en 4 filas habrá: 5 × 4 = 20
En una columna hay 4 , en 5 columnas habrá= 4 × 5 = 20
luego 5 × 4 = 4 × 5 = 20
De donde tenemos que: 5 × 4 = 4 × 5
PROPIEDAD CONMUTATIVA
El orden de los factores no altera el producto.
En una caja hay 5 4 = 20
En dos cajas 2 x (5 4) = 2 (20) = 40
Pero notamos que hay 2 5 = 10 columnas
→ (2 5) 4 = 10 4 = 40
Luego 2 (5 4) = (2 5) 4
Entonces:
PROPIEDAD ASOCIATIVA
Si asociamos factores de diversas formas,
se obtiene el mismo producto.
• Se tiene las siguientes manzanas.
• Si una manzana cuesta S/. 2, entonces pagaremos…
2 1 = S/. 2
precio cantidad PROPIEDAD DEL ELEMENTO NEUTRO
Todo número multiplicado por 1 da
como producto el mismo número.
•
Si nos regalan 4 manzanas, entonces no pagaremos nada.
4 0 = S/. 0
PROPIEDAD DEL ELEMENTO ABSORBENTE
Todo número multiplicado por cero, el producto es cero (0).
PROPIEDAD DISTRIBUTIVA
Al multiplicar un número por una adición o sustracción, se puede multiplicar el
número por cada elemento de la adición o sustracción y luego efectuar la operación
respectiva.
• Si tenemos manzanas y naranjas, ¿cuántas frutas tenemos?
En una fila hay 5 + 3
En 4 filas hay: 4 ( 5 + 3 ) = 32 frutas
4 x 5 + 4 x 3 = 32
20 + 12 = 32
32 = 32

46. INGENIO
4.° primaria
L U D O M A T I C
46
MULTIPLICACIÓN POR DOS CIFRAS
Multiplicando
Multiplicador
Producto
• Multiplicamos las unidades del
multiplicador por las cifras del
multiplicando.
• Luego, multiplicamos las decenas
del multiplicador por las cifras del
multiplicando, dejando un espacio
como se muestra.
• Finalmente, sumamos los productos .
MULTIPLICACIÓN POR 10
•
Si multiplicamos un número natural por 10, le agregamos un cero a la derecha del
número.
Ejemplo:
Si compramos
10 papayas
Pagaremos
S/. 2 10 = S/. 20
S/. 2
MULTIPLICACIÓN POR 100
•
Si multiplicamos un número natural por 100, le agregamos dos ceros a la derecha del
número.
Ejemplo:
CM DM UM C D U
2 6 4
5
2
1
1 3
2
2
6
1
4
0
2
1 3 4 7 4 2
1
2
S/. 3
Si compramos
100 manzanas
Pagaremos
S/. 3 100 = S/. 300

47. INGENIO
L U D O M A T I C
Aritmética
47
Completa los espacios en blanco.
Resolución:
a) Completamos los cuadros.
Completa los espacios en blanco.
Resolución:
a) Completamos los cuadros.
Relaciona los cuadros mostrados,
identificando la propiedad que se cumple.
Resolución:
a) Identificamos las propiedades.
Relaciona los cuadros mostrados,
identificando la propiedad que se cumple.
Resolución:
a) Identificamos las propiedades.
3 Determina el valor de verdad de las
siguientes proposiciones. Argumenta
tu respuesta.
• El 1 es el elemento absorbente. ( )
• 2 245 × 100 = 224 050 ( )
• 14 798 × 10 = 147 980 ( )
Resolución:
a) Analizamos las proposiciones.
•
Falso, porque el elemento
absorbente de la multiplicación
es el cero (0).
• Falso, porque 2245 × 100 = 224 500.
• Verdad, porque
14798 × 10 = 147 980.
3 Determina el valor de verdad de las
siguientes proposiciones. Argumenta
tu respuesta.
• El 1 es el elemento absorbente. ( )
• 2 245 × 100 = 224 050 ( )
• 14 798 × 10 = 147 980 ( )
Resolución:
a) Analizamos las proposiciones.
•
Falso, porque el elemento
absorbente de la multiplicación
es el cero (0).
• Falso, porque 2245 × 100 = 224 500.
• Verdad, porque
14798 × 10 = 147 980.
4 Para un candelabro, se necesita
4 velas. Si compro 100 cajas de
candelabros y cada una de ellas
contiene 9 candelabros, ¿cuántas
velas se necesitan para todos los
candelabros?
Resolución:
a) Sabemos que:
En una caja hay 9 candelabros.
En 100 cajas hay
9 × 100 = 900 candelabros.
b) Luego:
Un candelabro tiene 4 velas.
Se debe multiplicar la cantidad
de candelabros por el número de
velas.
900 × 4 = 3 600
c) Por lo tanto, se necesitan 3 600
velas
4 Para un candelabro, se necesita
4 velas. Si compro 100 cajas de
candelabros y cada una de ellas
contiene 9 candelabros, ¿cuántas
velas se necesitan para todos los
candelabros?
Resolución:
a) Sabemos que:
En una caja hay 9 candelabros.
En 100 cajas hay
9 × 100 = 900 candelabros.
b) Luego:
Un candelabro tiene 4 velas.
Se debe multiplicar la cantidad
de candelabros por el número de
velas.
900 × 4 = 3 600
c) Por lo tanto, se necesitan 3 600
velas
2
1
ANALIZAMOS Y APRENDEMOS
(23 12) 13 = 23 (12 13)
Propiedad
conmutativa
1 2583 = 2583 Propiedad
asociativa
450 12 = 12 450 Propiedad del
elemento neutro
CM DM UM C D U
7 6 2
1
4
4 5 7 4
4
4
9 4
CM DM UM C D U
7 6 2
1
4
6
4
7
5
6
7
2
4
4
4
1 2 1 9 8 4
3 1
1
2
(23 × 12) × 13 = 23 × (12 × 13) Propiedad asociativa
1 × 2 583 = 2 583 Propiedad del elemento
neutro de la multiplicación
450 × 12 = 12 × 450 Propiedad
conmutativa
(23×12) × 13 = 23×(12×13) Propiedad conmutativa
1 × 2 583 = 2 583
450 × 12 = 12 × 450
Propiedad asociativa
Propiedad del
elemento neutro
b) Relacionamos:
×
×

48. INGENIO
4.° primaria
L U D O M A T I C
48
x
x =
x =
x =
x
x =
x =
x =
Indicadores de evaluación
Indico las propiedades de la multiplicación.
Completo las operaciones de multiplicación.
Resuelvo problemas con multiplicación.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
23 451 × 12 143 352
457 x 100 281 412
3 258 x 44 45 700

49. INGENIO 49
¡Genial! Si
compramos 20
kilos, ¿cuánto
pagaremos?
¡Mira la oferta!
5 kilos de arroz
cuestan S/. 12.
TALLER
9 PROPORCIONALIDAD
RAZÓN GEOMÉTRICA
Es el cociente entre dos cantidades. Por ejemplo: la razón entre 12 y 5 es
De nuestro ejemplo:
a) Elaboramos nuestra tabla de proporcionalidad.
b) Piero y Lucero pagarán S/. 48.
PROPIEDAD FUNDAMENTAL DE LA PROPORCIÓN GEOMÉTRICA
El producto de los extremos es igual al producto de los medios.
× 2
× 4
× 2
× 4
N.° de kilos 5 10 20 40
Costo 12 24 48 96
PROPORCIONALIDAD DIRECTA
Extremos:
Medios:
48 × 5 = 20 × 12
240 = 240
¡Oh! Si aumenta el
número de kilos,
aumenta el costo.
Es decir, existe
una relación
proporcional.
Dos cantidades o más son proporcionales si, al aumentar o disminuir una de ellas, las otras
cantidades también aumentan o disminuyen.
PROPORCIÓN GEOMÉTRICA
Es la igualdad entre dos razones geométricas.
Ejemplo:
3
5
9
15
=

50. INGENIO
4.° primaria
L U D O M A T I C
50
Un auto ha dado 60 vueltas en
120 minutos. Calcula el tiempo que
tardará en recorrer 15 vueltas.
Resolución
a) Comprendemos.
Magnitud Magnitud
60 vueltas –––––– 120 minutos
15 vueltas –––––– x
b) Graficamos.
c) Efectuamos.
→ 60x=120×15→60x=1800
x = x = 30
d) Comunicamos la respuesta.
Al recorrer15vueltas,elautotardará
30 min.
Un auto ha dado 60 vueltas en
120 minutos. Calcula el tiempo que
tardará en recorrer 15 vueltas.
Resolución
a) Comprendemos.
Magnitud Magnitud
60 vueltas –––––– 120 minutos
15 vueltas –––––– x
b) Graficamos.
c) Efectuamos.
→ 60x=120×15→60x=1800
x = x = 30
d) Comunicamos la respuesta.
Al recorrer15vueltas,elautotardará
30 min.
Un saco de papas pesa 20 kg. ¿Cuánto
pesan 10 sacos de papas?
Resolución
a) Comprendemos.
Magnitud Magnitud
1 saco de papas –––––– 20 kg
10 sacos de papas –––––– x
Las magnitudes se incrementan.
b) Graficamos.
c) Efectuamos. Para pasar de la fila 1 a la fila
10 de kilos, bastará multiplicar por 10.
1 × 10 = 10 20 × 10 = 200
* Completamos la tabla.
d) Comunicamos la respuesta.
Un saco de papas pesa 20 kg. ¿Cuánto
pesan 10 sacos de papas?
Resolución
a) Comprendemos.
Magnitud Magnitud
1 saco de papas –––––– 20 kg
10 sacos de papas –––––– x
Las magnitudes se incrementan.
b) Graficamos.
c) Efectuamos. Para pasar de la fila 1 a la fila
10 de kilos, bastará multiplicar por 10.
1 × 10 = 10 20 × 10 = 200
* Completamos la tabla.
d) Comunicamos la respuesta.
3 En el aula del 4to A, hay 18 niñas y
12 niños. ¿Cuál es la razón entre niños
y niñas?
Resolución
a) Comprendemos.
N.o
de niñas =18
N.o
de niños = 12
Razón:
N.o
de niños
N.o
de niñas
b) Efectuamos la expresión:
razón:
N.o
de niños
N.o
de niñas =
c)
Comunicamos la respuesta:
Por cada dos niños hay tres niñas.
3 En el aula del 4to A, hay 18 niñas y
12 niños. ¿Cuál es la razón entre niños
y niñas?
Resolución
a) Comprendemos.
N.o
de niñas =18
N.o
de niños = 12
Razón:
N.o
de niños
N.o
de niñas
b) Efectuamos la expresión:
razón:
N.o
de niños
N.o
de niñas =
c)
Comunicamos la respuesta:
Por cada dos niños hay tres niñas.
4 Si 8 huevos pesan 600 gr, ¿cuánto
pesarán 24 huevos iguales a los
anteriores?
Resolución
a) Comprendemos.
Magnitud Magnitud
08 huevos –––––– 600 gr
24 huevos –––––– x
Las magnitudes se incrementan.
b) Graficamos.
c) Efectuamos las operaciones.
→ 8x = (24) × (600)
24 × 600
8
x = → x = 1800
d) Comunicamos la respuesta.
24 huevos pesan 1800 gr.
4 Si 8 huevos pesan 600 gr, ¿cuánto
pesarán 24 huevos iguales a los
anteriores?
Resolución
a) Comprendemos.
Magnitud Magnitud
08 huevos –––––– 600 gr
24 huevos –––––– x
Las magnitudes se incrementan.
b) Graficamos.
c) Efectuamos las operaciones.
→ 8x = (24) × (600)
24 × 600
8
x = → x = 1800
d) Comunicamos la respuesta.
24 huevos pesan 1800 gr.
2
1
ANALIZAMOS Y APRENDEMOS
Número de sacos 1 2 3 ... 10
Peso en kg 20 40 60 ...
Número de sacos 1 2 3 ... 10
Peso en kg 20 40 60 ... 200
N.° de vueltas 60 15
N.° de minutos 120 x
N.° de huevos 08 24
Peso 600 x

51. INGENIO
L U D O M A T I C
Aritmética
51
Indicadores de evaluación
Calculo la razón de dos cantidades.
Identifico las magnitudes que intervienen en un
problema.
Resuelvo problemas de magnitudes proporcionales.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4

52. INGENIO
52
¿Qué es la
división?
Dividir es tratar de partir una
cantidad (dividendo) en partes
iguales (divisor) y obtener un
resultado (cociente); pero, algunas
veces, sobra algo (residuo).
DIVISIÓN DE
NÚMEROS NATURALES
TALLER
10
Estas manzanas las
debemos repartir
entre 3 niños.
¿Cuánto le tocará
a cada uno?
Tenemos 13
manzanas en la
canasta.
DIVISIÓN
De nuestro ejemplo:
A cada niño le toca 4 manzanas y sobra 1 manzana.
13 3
–12 4
1
Divisor (d)
Dividendo(D)
Residuo(r)
Cociente (q)
Se cumple: D = d × q + r

53. INGENIO
L U D O M A T I C
Aritmética
53
Ejemplo 1:
Se debe repartir S/. 2 538 entre 7 personas. ¿Cuánto le toca a cada uno?
• Se inicia la división por las cifras de mayor
orden.
• Como 2 no se puede dividir entre 7, se
toma las dos primeras cifras: 27 ÷ 7. Da
como cociente 3 y sobra 4.
• Luego, se baja la siguiente cifra: 43 ÷ 7.
Da como cociente 6 y sobra 1.
• Se baja la siguiente cifra: 18 ÷ 7. Da como
cociente 2 y sobra 4.
Entonces: Cociente(q) = 362 Residuo(r) = 4
Se cumple Dividendo = Divisor × Cociente + residuo 2 538 = 7(362) + 4
2 538 = 2 534 + 4
2 538 = 2 538
7
362
CM DM UM C D U
2
2
5
1
4
4
-
3
3
2
1
1
-
8
8
4
4
Ejemplo 2:
Ayuda a Fernando a repartir 24 entre 3 del Parque de las Leyendas.
Solución
1.° reparto doy 3
Luego:
N.° de
monos
Cantidad
repartida
24
0
3
8
Cantidad
a repartir
Finalmente, a cada mono se debe dar 8
plátanos.
2.° reparto doy 3
3.° reparto doy 3
4.° reparto doy 3
5.° reparto doy 3
6.° reparto doy 3
7.° reparto doy 3
8.° reparto doy 3
24 – 3 = 21
21 – 3 = 18
18 – 3 = 15
15 – 3 = 12
12 – 3 = 9
9 – 3 = 6
6 – 3 = 3
3 – 3 = 0
Si el residuo es cero, la
división es exacta; caso
contrario es inexacta.

54. INGENIO
4.° primaria
L U D O M A T I C
54
Relaciona según corresponda:
Resolución:
•
Si la división es exacta, el residuo
es 0 (r = 0).
•
Si la división es inexacta, el residuo
es diferente a cero (r 0).
•
Si dividimos
2 582 ÷ 7 se tiene cociente = 368
y residuo = 6.
Por lo tanto:
Relaciona según corresponda:
Resolución:
•
Si la división es exacta, el residuo
es 0 (r = 0).
•
Si la división es inexacta, el residuo
es diferente a cero (r 0).
•
Si dividimos
2 582 ÷ 7 se tiene cociente = 368
y residuo = 6.
Por lo tanto:
Dada la siguiente división 342 ÷ 7.
Determina el valor de verdad de las
siguientes proposiciones:
I) El divisor es 6. ( )
II) El cociente es 48. ( )
III) El residuo es 7. ( )
Argumenta tu respuesta.
Resolución:
a) Dividimos:
342 7
28 48
62
56
6
I) Falso (F) porque el divisor es 7.
II)
Verdadera (V) porque el cociente
es 48.
III)Falso (F) porque el residuo es 6.
Dada la siguiente división 342 ÷ 7.
Determina el valor de verdad de las
siguientes proposiciones:
I) El divisor es 6. ( )
II) El cociente es 48. ( )
III) El residuo es 7. ( )
Argumenta tu respuesta.
Resolución:
a) Dividimos:
342 7
28 48
62
56
6
I) Falso (F) porque el divisor es 7.
II)
Verdadera (V) porque el cociente
es 48.
III)Falso (F) porque el residuo es 6.
3 Se divide cierto número N entre 12,
y se obtiene como cociente 321 y
residuo 6. Determina N y elabora una
estrategia de solución.
Resolución
a) Sabemos que:
D = d × q + r
↓
N = (12) (321) + 6
N = 3 852 + 6
N = 3 858
b) Por lo tanto:
N = 3 858
3 Se divide cierto número N entre 12,
y se obtiene como cociente 321 y
residuo 6. Determina N y elabora una
estrategia de solución.
Resolución
a) Sabemos que:
D = d × q + r
↓
N = (12) (321) + 6
N = 3 852 + 6
N = 3 858
b) Por lo tanto:
N = 3 858
4 Un albañil debe construir 4 muros
de igual dimensión. Para ello, tiene
7 013 ladrillos. Determina cuántos
ladrillos tendrá cada muro. Elabora
una estrategia de solución.
Resolución:
a) Sabemos que son 7 013 ladrillos
y que deben ser 4 muros.
b) Entonces, dividamos 7013 ÷ 4
7013 4
4 1753
30
28
21
20
13
12
1
c)
Por lo tanto, cada muro tendrá
1 753 ladrillos y sobrará 1 ladrillo.
4 Un albañil debe construir 4 muros
de igual dimensión. Para ello, tiene
7 013 ladrillos. Determina cuántos
ladrillos tendrá cada muro. Elabora
una estrategia de solución.
Resolución:
a) Sabemos que son 7 013 ladrillos
y que deben ser 4 muros.
b) Entonces, dividamos 7013 ÷ 4
7013 4
4 1753
30
28
21
20
13
12
1
c)
Por lo tanto, cada muro tendrá
1 753 ladrillos y sobrará 1 ladrillo.
2
1
ANALIZAMOS Y APRENDEMOS
División exacta r = 6
División inexacta r = 0
2 582 ÷ 7 r 0
División exacta r = 6
División inexacta r = 0
2 582 ÷ 7 r 0

55. INGENIO
L U D O M A T I C
Aritmética
55
÷
÷
Indicadores de evaluación
Identifico los elementos de la división.
Reconozco las divisiones exactas e inexactas.
Resuelvo operaciones con división.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
8 460 ÷ 235 25
8 975 ÷ 359 36
8 841 ÷ 421 21
235
CM DM UM C D U
9 5 8 3

56. INGENIO
56
OPERACIONES
COMBINADAS
TALLER
11
Ellos son mis
compañeros
del salón.
¿Cuántos
son?
Habrá que hacer
diferentes cálculos.
Lo lograremos
mediante
operaciones
combinadas.
Operaciones combinadas
Consiste en hacer operaciones de suma, resta, multiplicación, etc; para ello también
utilizamos los signos de colección como paréntesis ( ), corchete [ ], etc.
De nuestro ejemplo:
a) Expresamos numéricamente el
número de estudiantes: 4 × 5 + 2
b) Resolvemos
4 × 5 + 2
20 + 2
22
c) Comunicamos el resultado.
Son 22 alumnos en mi salón.
Orden al operar:
1. Calcula las operaciones que hay dentro
de los signos de colección.
2. Calcula la multiplicación y división en el
orden que aparecen.
3. Calcula la suma y resta en el orden en
que aparecen.
5
4

57. INGENIO
L U D O M A T I C
Aritmética
57
Lea la siguiente frase y escribe la
expresión numérica:
“Al triple de 40, súmale el doble de
18”.
Resolución:
a) Escribimos la expresión numérica.
triple de 40 = 3 × 40
Doble de 18 = 2 × 18
3 × 40 + 2 × 18
b) Resolvemos.
3 × 40 + 2 × 18
120 + 36
156
c) La expresión es igual a 156.
Lea la siguiente frase y escribe la
expresión numérica:
“Al triple de 40, súmale el doble de
18”.
Resolución:
a) Escribimos la expresión numérica.
triple de 40 = 3 × 40
Doble de 18 = 2 × 18
3 × 40 + 2 × 18
b) Resolvemos.
3 × 40 + 2 × 18
120 + 36
156
c) La expresión es igual a 156.
Calcula el resultado de las siguientes
operaciones combinadas.
E = 20 × (4 – 2) + 480 ÷ (5 + 3)
Comunica tu resultado.
Resolución:
Respetamos el orden:
1. Se resuelven las operaciones que están
entre signos de agrupación ( ), [ ].
2. Luego las multiplicaciones o divisiones.
3. Finalmente las adiciones o
sustracciones.
E = 20 × (4 – 2) + 480 ÷ (5 + 3)
20 × (2) + 480 ÷ (8)
40 + 60
100
El resultado es E = 100.
Calcula el resultado de las siguientes
operaciones combinadas.
E = 20 × (4 – 2) + 480 ÷ (5 + 3)
Comunica tu resultado.
Resolución:
Respetamos el orden:
1. Se resuelven las operaciones que están
entre signos de agrupación ( ), [ ].
2. Luego las multiplicaciones o divisiones.
3. Finalmente las adiciones o
sustracciones.
E = 20 × (4 – 2) + 480 ÷ (5 + 3)
20 × (2) + 480 ÷ (8)
40 + 60
100
El resultado es E = 100.
Marca y resuelve la expresión numérica
correcta. Lucho compró con S/. 100
4 cuadernos a S/. 6 cada uno y 6 resaltadores
a S/. 2 cada uno. ¿Cuánto recibirá de vuelto?
100 – 4 × 6 + 6 × 2
100 + 4 × 6 – 6 × 2
100 – (4 × 6 + 6 × 2)
Resolución:
a) La expresión correcta es la alternativa C
pueshayquecalcularloquequeda,luego
de haber efectuado el paréntesis ( ).
b) Resolvemos.
100 – (4 × 6 + 6 × 2)
100 – ( 24 + 12 )
100 – 36
64
c) Lucho recibe de vuelto S/. 64.
Marca y resuelve la expresión numérica
correcta. Lucho compró con S/. 100
4 cuadernos a S/. 6 cada uno y 6 resaltadores
a S/. 2 cada uno. ¿Cuánto recibirá de vuelto?
100 – 4 × 6 + 6 × 2
100 + 4 × 6 – 6 × 2
100 – (4 × 6 + 6 × 2)
Resolución:
a) La expresión correcta es la alternativa C
pueshayquecalcularloquequeda,luego
de haber efectuado el paréntesis ( ).
b) Resolvemos.
100 – (4 × 6 + 6 × 2)
100 – ( 24 + 12 )
100 – 36
64
c) Lucho recibe de vuelto S/. 64.
Una empresa editora debe repartir
6 448 diarios a 4 puestos de ventas en
partes iguales. Si cada diario cuesta S/. 2,
¿cuánto debe recaudar cada puesto?
Elabora una estrategia de solución.
Resolución:
a) Debemos repartir 6 448 diarios en
4 puestos.
b) Cada diario cuesta S/. 2.
c) (6 448 ÷ 4) × 2
d) Efectuamos.
(6 448 ÷ 4) × 2
1 612 × 2
3 224
e) Comunicamos el resultado.
La empresa recaudó S/. 3 224 de
cada puesto.
Una empresa editora debe repartir
6 448 diarios a 4 puestos de ventas en
partes iguales. Si cada diario cuesta S/. 2,
¿cuánto debe recaudar cada puesto?
Elabora una estrategia de solución.
Resolución:
a) Debemos repartir 6 448 diarios en
4 puestos.
b) Cada diario cuesta S/. 2.
c) (6 448 ÷ 4) × 2
d) Efectuamos.
(6 448 ÷ 4) × 2
1 612 × 2
3 224
e) Comunicamos el resultado.
La empresa recaudó S/. 3 224 de
cada puesto.
2
1
ANALIZAMOS Y APRENDEMOS
4
3

58. INGENIO
4.° primaria
L U D O M A T I C
58
+
× ×
+
× ×
Indicadores de evaluación
Establezco el orden en el cálculo de operaciones
combinadas.
Establezco una representación gráfica de
operaciones combinadas.
Resuelvo problemas mediante operaciones
combinadas.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
S/. 42 310 S/. 134 000

59. PROPORCIONALIDAD CON NÚMEROS NATURALES
PROYECTO DE APRENDIZAJE N.0 4
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1. Situación problemática
En las actividades que realizamos diariamente, usamos con mucha frecuencia frases
como tengo el doble; tienes el triple etc. Estas frases utilizan la proporcionalidad
directa de ciertas cantidades; por ello, se hace indispensable representarlas e
interpretarlas.
2. Finalidad
•
Realizar operaciones que se apliquen la proporcionalidad.
• Reconocer la importancia de la proporcionalidad.
3. Recursos materiales
Papeles.
Plumones.
Lapiceros.
Regla.
4. Etapas y actividades
5. Evaluación
1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de 4 estudiantes.
Realizan una lista de
expresiones donde se emplea
la proporcionalidad directa.
Escriben en el
papelote dichas
expresiones y se las
representa gráfica y
matemáticamente.
Exponen su
trabajo.
INGENIO 59

60. INGENIO
60
UNIDAD
5
Educación en derechos humanos
Aprendemos a:
• Resolver operaciones combinadas en N.
• Reconocer y representar fracciones.
•
Calcular la suma y la diferencia de las
fracciones heterogéneas, utilizando
fracciones homogéneas.
Cultivamos valores
•
Educación para los
derechos humanos.
•
Respeto.
Observa la imagen y contesta.
¿Sabes cuáles son tus derechos como niño y como estudiante?
¿Consideras que es importante conocer los derechos humanos?
FRACCIONES

61. INGENIO 61
1. Formamos equipos de 4 integrantes.
2. Cada equipo se responsabiliza por
traer: cartulinas de color celeste,
verde y rojo. Una regla, de 30 cm,
plumones, lápiz y tijera.
J U G A N D O C O N
F R A C C I O N E S
Nos organizamos
Jugamos y aprendemos
1. Se dibujará las siguientes figuras
geométricas: 2 cuadrados,
2 rectángulos, 2 circunferencias.
2. El cuadrado medira 20 cm de lado.
El rectángulo medira: largo 30 cm
y ancho 15 cm. La circunferencia
medirá 20 cm de radio.
3. Se corta las figuras.
4. Los cuadrados se dividen: Uno en
2 partes y el otro en cuatro partes.
5. Los rectángulos se dividen: Uno en
3 partes iguales y el otro en 9 como
muestra la figura. Donde a = 10 cm
y b = 5 cm.
6. La circunferencia se divide en dos
partes y cuatro.
7. A cada parte dividida se le asigna
la fracción que le corresponde y se
busca: 1/3 ; 5/9 ; 1/2 ; 3/4.
5
LABORATORIO
3a
3b
a
b

62. INGENIO
62
FRACCIONES
TALLER
12
¡Fácil! Se representa por
el número de partes
(numerador) respecto a
un total de partes iguales
(denominador) en que se ha
divido una unidad o grupo.
¿Qué parte
del total te
comerías?
Me comeré
las tres 3
primeras
mandarinas.
FRACCIÓN
De nuestro ejemplo:
a)
Tenemos 12 mandarinas. De ellas, la niña comerá 3 mandarinas; entonces, lo que
la niña comerá representa:
La fracción es un número que se obtiene al dividir una totalidad en partes iguales.
Numerador
Denominador
Se lee tres doceavos.
Ejemplo 2
Escribe la fracción que representa la parte sombreada:
=
Partes sombreadas.
Total de partes.
Ejemplo 3
Colorea las partes necesarias para representar la fracción .
3
12
¿Cómo se representa
una fracción
matemáticamente?

63. INGENIO
L U D O M A T I C
Aritmética
63
CLASIFICACIÓN DE FRACCIONES
Las fracciones pueden ser:
Fracciones homogéneas porque tienen igual denominador.
Fracciones heterogéneas porque tienen diferente denominador.
COMPARACIÓN DE DOS FRACCIONES
a) Si las fracciones son homogéneas, es mayor la fracción que tiene mayor numerador.
Ejemplo: y como 7 4, entonces
b) Si las fracciones son heterogéneas, se multiplica las fracciones de manera cruzada
(denominador con numerador) y se comparan.
i)
ii)
FRACCIONES EQUIVALENTES
Dos fracciones son equivalentes si representan la misma fracción.
La parte
sombreada es
3
4
=
6
8
La parte
sombreada es
Son fracciones equivalentes
Para determinar las fracciones equivalentes, se multiplica (amplificación) o divide
(simplificación) por una misma cantidad el numerador y denominador.
Ejemplo:
2
3
4
6
8
12
16
24
= = =
54
81
18
27
6
9
2
3
= = =
a) Por amplificación Por Simplificación
x 2 x 2
x 2
÷ 3 ÷ 3 ÷ 3
3 x 6 4 × 5 18 20
2 x 5 3 × 1 10 3
2
3
1
5
3
5
4
6

64. INGENIO
4.° primaria
L U D O M A T I C
64
Dadas las siguientes fracciones:
3
5
2
7
1
2
; ;
Ordena de menor a mayor. Argumenta
tu respuesta.
Resolución:
a)
Para ordenar las fracciones
heterogéneas, debemos homogenizar
lo siguiente:
3
5
2
7
1
2
7 2
7 2
5 2
3 2
5 7
5 7
× ×
× ×
× ×
× ×
× ×
× ×
; ;
42
70 ;
20
70 ;
35
70
b) Luego, nos fijamos en el numerador.
42
70
35
70
20
70
c) Ordenamos y mostramos el resultado:
2
7
1
2
3
5
Dadas las siguientes fracciones:
3
5
2
7
1
2
; ;
Ordena de menor a mayor. Argumenta
tu respuesta.
Resolución:
a)
Para ordenar las fracciones
heterogéneas, debemos homogenizar
lo siguiente:
3
5
2
7
1
2
7 2
7 2
5 2
3 2
5 7
5 7
× ×
× ×
× ×
× ×
× ×
× ×
; ;
42
70 ;
20
70 ;
35
70
b) Luego, nos fijamos en el numerador.
42
70
35
70
20
70
c) Ordenamos y mostramos el resultado:
2
7
1
2
3
5
Piero compra dos pizzas de igual
tamaño. Él y Lucero comen la cantidad
sombreada. ¿Alguno de ellos comió
más?
Resolución:
Observamos y comprendemos que:
a) Pierocome
2
4
delapizza,Lucerocome
los
4
8
b)
Graficamente, observamos que
comen lo mismo. Además
= =
4
8
2 2
4 2
2
4
×
×
entonces
2
4
y
4
8
son equivalentes.
c) Por lo tanto, Lucero y Piero comieron
igual cantidad de pizza.
Piero compra dos pizzas de igual
tamaño. Él y Lucero comen la cantidad
sombreada. ¿Alguno de ellos comió
más?
Resolución:
Observamos y comprendemos que:
a) Pierocome
2
4
delapizza,Lucerocome
los
4
8
b)
Graficamente, observamos que
comen lo mismo. Además
= =
4
8
2 2
4 2
2
4
×
×
entonces
2
4
y
4
8
son equivalentes.
c) Por lo tanto, Lucero y Piero comieron
igual cantidad de pizza.
Establece la verdad de las siguientes
proposiciones, argumentando tu
respuesta.
I)
2
3
y
16
24
son fracciones equivalentes ( )
II)
2
3
5
6
( )
III)
4
7
3
7
( )
Resolución
I) Verdadero,porque
16
24
2 8
3 8
2
3
×
×
además:
2
3
y
16
24
son fracciones equivalentes.
II) Verdadero, porque:
2
3
5
6
; entonces, 12 15 ∴
2
3
5
6
III)
Verdadero, porque son fracciones
h o m o g é n e a s ; e n t o n c e s ,
comparamos los numeradores;
4
7
3
7
.
Establece la verdad de las siguientes
proposiciones, argumentando tu
respuesta.
I)
2
3
y
16
24
son fracciones equivalentes ( )
II)
2
3
5
6
( )
III)
4
7
3
7
( )
Resolución
I) Verdadero,porque
16
24
2 8
3 8
2
3
×
×
además:
2
3
y
16
24
son fracciones equivalentes.
II) Verdadero, porque:
2
3
5
6
; entonces, 12 15 ∴
2
3
5
6
III)
Verdadero, porque son fracciones
h o m o g é n e a s ; e n t o n c e s ,
comparamos los numeradores;
4
7
3
7
.
Alessandra divide su torta de
cumpleños en 15 partes iguales. Si
reparte 11 pedazos, ¿qué fracción
de la torta le queda? Elabora una
estrategia de solución.
Resolución
a)
Dividamos la torta en 15 partes
iguales.
b)
Luego, sombreamos 11 partes para
repartirla. Luego, las partes que nos
quedan son las que sobran.
c) Por lo tanto, queda de la torta.
Alessandra divide su torta de
cumpleños en 15 partes iguales. Si
reparte 11 pedazos, ¿qué fracción
de la torta le queda? Elabora una
estrategia de solución.
Resolución
a)
Dividamos la torta en 15 partes
iguales.
b)
Luego, sombreamos 11 partes para
repartirla. Luego, las partes que nos
quedan son las que sobran.
c) Por lo tanto, queda de la torta.
2
1
ANALIZAMOS Y APRENDEMOS
4
3

65. INGENIO
L U D O M A T I C
Aritmética
65
a)
b)
a)
b)
Indicadores de evaluación
Represento gráficamente una fracción.
Calculo la fracción de una cantidad.
Resuelvo problemas con datos fraccionarios.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
cinco sextos
siete novenos
seis décimos
tres cuartos

66. INGENIO
66
¿Cómo se opera
con las fracciones
homogéneas?
¡Muy fácil! Se suma o resta
los numeradores de las
fracciones, manteniendo el
denominador.
OPERACIONES CON
FRACCIONES
TALLER
13
Doña Luisa,
¿qué parte de
la tela vendió
en los dos días?
Doña Luisa vendió los de una tela
el día lunes y de la misma tela, el
martes. ¿Cuánto vendió?
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HOMOGÉNEAS
De nuestro ejemplo:
E =
2
5
1
5
2 1
5
3
5
+ =
+
= ; Doña Luisa vendió de la tela.
Ejemplos:
Sumar las partes sombreadas.
Azul : negra: 2
8
3
8
2 3
8
5
8
+ =
+
=
A = 5
8
2
8
5 2
8
3
8
− =
−
=
B =
6
7
2
7
6 2
7
4
7
− =
−
=

67. INGENIO
L U D O M A T I C
Aritmética
67
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HETEROGÉNEAS
Para hallar la suma de las fracciones heterogéneas, se convierte en homogéneas y se
procede a realizar la operación.
Resuelve:
a)
4
5
3
10
4
5
3
10
8
10
3
10
8 3
10
11
10
2
2
+ → + =+ =
+
=
×
×
b)
1
2
5
8
1
2
5
8
4
8
5
8
4 5
8
9
8
4
4
+ → + =+ =
+
=
×
×
c) Sumar las partes sombreadas:
1
4
3
8
1
4
3
8
2
8
3
8
2 3
8
5
8
2
2
+ ⇒ + =+ =
+
=
×
×
d)
3
4
3
8
3
4
3
8
6
8
3
8
6 3
8
3
8
2
2
− → − = − =
−
=
×
×
e) Restar las partes sombreadas:
3
8
1
4
3
8
1
4
3
8
2
8
3 2
8
1
8
2
2
− = − = − =
−
=
×
×
MULTIPLICACIÓN DE FRACCIONES
En una clase de 24 alumnos, aprobaron el examen de matemática y de ellos con
notas mayores a 17. ¿Cuántos alumnos han obtenido notas sobresalientes?
a) Representar gráficamente.
del total de alumnos que aprobaron
el examen es 16.
de los
2
3
de los alumnos
que obtuvieron notas
sobresalientes son 4.
b) Numéricamente.
2
3
24
1
1
4
2 24 1
3 1 4
× × =
× ×
× ×
= 4
8
2
1

68. INGENIO
4.° primaria
L U D O M A T I C
68
Vanessa compró un pan de molde
dividido en 20 partes iguales, repartió 12 de
ellas y se comió 4. ¿Qué fracción de pan
queda? Elabora una estrategia de solución.
Resolución
a)
Sabemos que el pan de molde está
dividido en 20 partes iguales.
b) Graficamos:
c) Calculamos.
i)
Luego, reparte 12 de ellas quedando
20
20
12
20
20 12
20
8
20
− =
−
=
ii) Luego se come 4 partes:
8
20
4
20
8 4
20
4
20
− =
−
=
d) Comunicamos la respuesta.
Por lo tanto, le sobra del pan de
molde.
Vanessa compró un pan de molde
dividido en 20 partes iguales, repartió 12 de
ellas y se comió 4. ¿Qué fracción de pan
queda? Elabora una estrategia de solución.
Resolución
a)
Sabemos que el pan de molde está
dividido en 20 partes iguales.
b) Graficamos:
c) Calculamos.
i)
Luego, reparte 12 de ellas quedando
20
20
12
20
20 12
20
8
20
− =
−
=
ii) Luego se come 4 partes:
8
20
4
20
8 4
20
4
20
− =
−
=
d) Comunicamos la respuesta.
Por lo tanto, le sobra del pan de
molde.
Resuelve y relaciona las siguientes
columnas:
Resolución:
Desarrollamos las operaciones y calculamos
los resultados.
Resuelve y relaciona las siguientes
columnas:
Resolución:
Desarrollamos las operaciones y calculamos
los resultados.
3
Establece la verdad de las siguientes
proposiciones. Argumenta tu respuesta.
I) 2
5
1
5
3
5
+ = ( )
II) 2
5
3
4
21
20
+ = ( )
III) 3
4
1
3
5
12
− = ( )
Resolución
I) Verdadero (V): como son homogéneos
se suman los numeradores.
2
5
1
5
2 1
5
3
5
+ =
+
=
II) Falso (F): 2
5
3
4
2
5
3
4
8
20
15
20
4
4
5
5
+ = + = +
x
x
x
x
=
8 15
20
23
20
+
=
III)Verdadero(V):porque:
3
4
1
3
3
4
1
3
3
3
4
4
− = −
x
x
x
x
= − =
−
=
9
12
4
12
9 4
12
5
12
3
Establece la verdad de las siguientes
proposiciones. Argumenta tu respuesta.
I) 2
5
1
5
3
5
+ = ( )
II) 2
5
3
4
21
20
+ = ( )
III) 3
4
1
3
5
12
− = ( )
Resolución
I) Verdadero (V): como son homogéneos
se suman los numeradores.
2
5
1
5
2 1
5
3
5
+ =
+
=
II) Falso (F): 2
5
3
4
2
5
3
4
8
20
15
20
4
4
5
5
+ = + = +
x
x
x
x
=
8 15
20
23
20
+
=
III)Verdadero(V):porque:
3
4
1
3
3
4
1
3
3
3
4
4
− = −
x
x
x
x
= − =
−
=
9
12
4
12
9 4
12
5
12
Alessandra tiene un collar de perlas. Si
la mitad de las perlas son moradas, la
cuarta parte son azules y 25 son doradas.
Calcula el número de perlas del collar y
elabora una estrategia de solución.
Resolución
Sabemos que:
x
2 son morados
x
4 son azules
25 son doradas.
Nos ayudamos de un gráfico:
moradas azules doradas
25
calculemos:
2 2 3
2 4 2 2 4 4 4 4
x x x x x x x
×
+ = + = + =
×
El área restante es
x
x x
4
25 25 4 100
= → = × → =
Comunicamos la respuesta.
Por lo tanto, el número de perlas es 100.
Alessandra tiene un collar de perlas. Si
la mitad de las perlas son moradas, la
cuarta parte son azules y 25 son doradas.
Calcula el número de perlas del collar y
elabora una estrategia de solución.
Resolución
Sabemos que:
x
2 son morados
x
4 son azules
25 son doradas.
Nos ayudamos de un gráfico:
moradas azules doradas
25
calculemos:
2 2 3
2 4 2 2 4 4 4 4
x x x x x x x
×
+ = + = + =
×
El área restante es
x
x x
4
25 25 4 100
= → = × → =
Comunicamos la respuesta.
Por lo tanto, el número de perlas es 100.
2
1
ANALIZAMOS Y APRENDEMOS
a)
b)
3
4
2
4
2
5
1
3
+





 −





 +
3
5
2
3
2
7
1
7
+ − +






71
60
a) 3
5
2
3
2
7
1
7
+ − +






b) 3
4
2
4
2
5
1
3
+





 −





 +
3
5
2
3
2 1
7
3
3
5
5
x
x
x
x
+ −
+






5
4
2
5
1
3
−





 +
9
15
10
15
3
7
19
15
3
7
+ − → −
19
15
3
7
7
7
15
15
x
x
x
x
−
133
105
45
105
−
133 45
105
88
105
−
=
5
4
2
5
1
3
25
20
8
20
1
3
5
5
4
4
x
x
x
x
−





 + → −





 +
17
20
1
3
17
20
1
3
3
3
20
20
+ = +
x
x
x
x
51
60
20
60
71
60
+ =
Donde “x” es
el número de
perlas.
4

69. INGENIO
L U D O M A T I C
Aritmética
69
7
2
3
2
4
5
2
5
3
4
1
4
−





 + +











 + +






7
2
3
2
4
5
2
5
3
4
1
4
−





 + +











 + +






7
5
1
5
4
5
4
5
+ − =
2
5
3
2
1
3
88
42
+





 + =
5
8
2
8
7
4
3
4
17
18
−





 + −











 =
7
5
1
5
4
5
4
5
+ − =
2
5
3
2
1
3
88
42
+





 + =
5
8
2
8
7
4
3
4
17
18
−





 + −











 =
Indicadores de evaluación
Calculo el valor de una operación combinada
con fracciones.
Determino el valor de verdad de proposiciones
con fracciones.
Resuelvo problemas de operaciones combinadas
con fracciones.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4

70. PROYECTO DE APRENDIZAJE N.0 5
INGENIO
FRACCIONES
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1. Situación problemática
En las actividades que realizamos a diario, encontramos diversas expresiones que
permiten comunicarnos y manifestar lo que deseamos; por ejemplo: un cuarto de
pollo, medio litro de limonada, tres cuartos de fideos etc. Estas expresiones hacen
referencia a las fracciones y, por ello, es sumamente importante conocerlas.
2. Finalidad
• Reconocer el uso de las fracciones en las actividades que realizamos a diario.
3. Recursos materiales
Papelote.
Regla.
Cinta adhesiva.
Plumones.
Lapiceros.
4. Etapas y actividades
5. Evaluación
1.ª etapa 2.ª etapa
Forman grupos de 4 estudiantes.
Realizan una lista de expresiones más
comunes donde se utilice las fracciones.
Escriben las expresiones en un papelote.
Matematizan estas expresiones.
Ejemplo:
Un cuarto de pollo = 1/4 de pollo.
Exponen su trabajo y lo pegan en las
paredes del aula.
70

71. UNIDAD
6
Cultivamos valores
•
Educaciónenvalores
y formación ética.
• Tolerancia.
Aprendemos a:
•
Reconocer la definición de los números
decimales.
•
Convertirycompararnúmerosdecimales.
•
Resolver operaciones con números
decimales.
Observa la imagen y contesta.
¿Por qué es importante practicar los valores?
¿En tu vida diaria practicas valores? Indica cuáles.
NÚMEROS
DECIMALES
Educación en valores

72. INGENIO
72
Nombre Tiempo
1.
2.
3.
4.
TOTAL
1.
Los equipos eligen a su primer partici-
pante, quien recibirá una hoja con la
siguiente operación:
a) 25 × (12 – 2) + 45 × (100 ¸ 25)
Se escribe en el cuadro el tiempo que
tarda en resolver el ejercicio.
2.
Cada uno de los 3 alumnos restantes
recibirá una operación.
a) (17 – 2) × 10 – (25 ¸ 5)
b) [(47 – 2) ¸ 9] × 20
c) [(13 + 7) × 20] ¸ 8
3.
Cada uno de los tiempos empleados en
resolver los ejercicios serán registrados en
la tabla .
4.
Luego que todos los integrantes han
resuelto los problemas, se suma todos los
tiempos.
Nos organizamos
1. Forman equipos de cuatro (4) integrantes.
2. Cada equipo llevará un cronómetro y una
hoja A-4 en la cual realizará un cuadro
(fig. 1).
Jugamos y aprendemos
Gana el equipo que
termine en menos
tiempo.
Fig. 1
6
LABORATORIO
H A B I L I D A D
N U M É R I C A

73. INGENIO 73
NÚMEROS DECIMALES
b) Al dividir la unidad en 100 partes, cada parte es 1 centésimo.
S/. 7,50
S/. 7,50
S/. 9,50
S/. 9,50
S/. 9,50
S/. 9,50
S/. 7,50
S/. 6,50
S/. 9,50 S/. 8,50
1 unidad = 10 décimos
1 unidad = 100 centésimos
Gráficamente:
1 décimo =
1 centésimo =
1
10
1
100
= 0,1
= 0,01
Es decir:
a) Al dividir la unidad en 10 partes, de acuerdo a los ejemplos que veremos,
obtenemos que cada parte es 1 décimo.
0,1 =
Fracción
decimal
Número
decimal
1
10
TALLER
NÚMEROS DECIMALES
14
Observa que los
precios son números
que tienen una coma.
¿Cómo se lee esos
números?
Vamos al
supermercado para
conocer los precios
de los juguetes.
¿Qué es un número
decimal?
Un número decimal
se obtiene de una
fracción al efectuar
la división entre sus
términos.
En este taller, vamos a trabajar
con números decimales a partir
de fracciones decimales.

74. INGENIO
4.° primaria
L U D O M A T I C
74
1
10
, 1
100
, 1
1000
… son fracciones decimales.
0,1; 0,01; 0,001 son sus representaciones decimales.
Ejemplos: escribe su expresión decimal.
Se escribe el numerador, luego se coloca la coma a tantas cifras como ceros tenga el
denominador. Se cuenta de derecha a izquierda.
Observa la ubicación de los números decimales en el Tablero de Valor Posicional.
Centena Decena Unidad Coma Décimo Centésimo Milésimo Se lee
C D U , d c m
0 , 5 Cinco décimos
4 , 8
Cuatro enteros,
ocho décimos
1 2 , 3 2
Doceenteros,treinta
y dos centésimos
7 , 1 2 2
Siete enteros, ciento
veintidós milésimos
CONVERSIÓN DE UNA FRACCIÓN DECIMAL EN UN NÚMERO DECIMAL
LECTURA Y ESCRITURA DE NÚMEROS DECIMALES
=
=
4
10
15
100
= 0,4
= 0,15
=
6
100
= 0,06

75. INGENIO
L U D O M A T I C
Aritmética
75
Ejemplo 1: Completa el Tablero de Valor Posicional
Ejemplo 2: Escribe la lectura de los siguientes números decimales.
COMPARACIÓN DE NÚMEROS DECIMALES
• Se compara primero la parte entera.
•
Si la parte entera fuera igual, comparamos la parte decimal, empezando por los
décimos. Si estos fueran iguales, continuamos con los centésimos hasta encontrar
una desigualdad.
Ejemplo:
Ordena las tallas de los siguientes niños en metros e indica quién de ellos es
el más alto.
Respuesta:
Miguel es el más alto del grupo, siendo su talla de 1,61 m.
1,61 1,56 1,52 1,42 1,16
14,01 Catorce enteros, un centésimo.
Ejemplo
2,22 Dos enteros, veintidós centésimos.
3, 42 5,12
5, 12 5, 08
7, 2 8 7, 2 5
3, 42 5, 12
5, 12 5, 08
7, 28 7, 25
Número D U d c m Se lee
16,08 1 6, 0 8
Dieciséis enteros, ocho
centésimos
8,25 8, 2 5
Ocho enteros, veinticinco
centésimos
Piero Paola Lucero Johan Miguel
1,16 1,52 1,56 1,42 1,61
=
=
=

76. INGENIO
4.° primaria
L U D O M A T I C
76
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Representa en fracción y en expresión
decimal la parte sombreada.
Comunica tu respuesta.
Resolución:
a)
Representamos en fracción la
parte sombreada.
Número de partes = 10
Parte sombreada = 4
4
10
Se lee: cuatro décimos.
b)
La parte sombreada equivale en
números decimales a 0,4.
4
10
= 0,4
Escribe una fracción equivalente a
y su respectiva expresión decimal.
Resolución:
a)
Buscamos una fracción equivalente
a
23
20
=
5
5
×
×
23
20
115
100
b)
Escribimos su expresión decimal
= 1,15
115
100
23
20
Completa el Tablero de Valor Posicional.
Número D U d c m Se lee
6,23
4, 0 5
1 2, 1 2 4
8,2
Resolución:
Completamos
Número D U d c m Se lee
6,23 6, 2 3
Seis enteros veintitrés
centésimos.
4,05 4, 0 5
Cuatro enteros
cinco centésimos.
12,124 1 2, 1 2 4
Doce enteros
ciento venticuatro
milésimos
8,2 8, 2
Ocho enteros dos
décimos.
Compara y escribe el símbolo , o =
donde corresponde:
0,72
2,5
0,82
7,2
0,25
0,98
Resolución:
a)
Ubicamos los números en el Tablero de Valor
Posicional y colocamos los símbolos , .
D U d c
7 , 2 0
0 , 2 5
0 , 9 8
D U d c
0 , 7 2
2 , 5 0
0 , 8 2
b)
Por lo tanto:
0,72 7,2
2,5 0,25
0,82 0,98

77. INGENIO
L U D O M A T I C
Aritmética
77
Indicadores de evaluación
Convierto fracciones decimales en números
decimales.
Establezco una relación de orden entre números
decimales.
Represento las partes sombreadas en números
decimales.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Escribe fracciones equivalentes a
1
25
;
4
5
;
6
50
y su respectiva
representación decimal.
Completa la siguiente tabla.
Número Se lee
Tres décimos.
2,12
Seis enteros, doce centésimos.
0,132
14, 232
Representa en números decimales
las partes sombreadas.
Azul =
Rojo =
S/. 324, 8
S/. 2, 52
S/. 5, 32
S/. 324, 12
S/. 1, 80
S/. 5, 6
Compara el precio de los objetos
mostrados y escribe los símbolos ,
o = según corresponda.

78. INGENIO
78
OPERACIONES CON
NÚMEROS DECIMALES
De nuestro ejemplo:
a) Calculamos el
costo total de los
regalos.
c) Por lo tanto nos sobra S/. 10,68.
Ejemplo 1: Calculamos la suma y diferencia.
Ejemplo 2:
Si Erick mide 1,72 m y Piero 1,41 m, ¿cuánto le falta crecer a Piero para
alcanzar la talla de Erick?
a) Sabemos que:
– Erick = 1,72 m
– Piero = 1,41 m
c) A Piero le falta crecer 0,31 m para alcanzar la talla de Erick.
b)
Para establecer la
diferencia, calculamos
1,72 m – 1,41 m.
S/. 23,2 S/. 14,12
ADICIÓN Y SUSTRACCIÓN DE NÚMEROS DECIMALES
1 0 4 , 7 2
4 8 , 6 3
1 5 3 , 3 5
4 2 , 3 2 5
1 6 , 2 1 9
2 6 , 1 0 6
+ -
-
1, 7 2
1, 4 1
0, 3 1
D U , d c
2 3 , 2 0
1 4 , 1 2
3 7 , 3 2
b) El costo de los regalos
es de S/. 37,32.
Para saber si alcanza
el dinero, calculamos
S/. 48 – S/. 37,22.
D U , d c
4 8 , 0 0
3 7 , 3 2
1 0 , 6 8
-
+
TALLER
15
Deseo comprar un
osito y un arreglo
floral para regalarle
a Paolita por su
cumpleaños.
Tenemos ahorrados
S/. 48 ¿Nos alcanza
el dinero?
Se escribe los números uno
debajo del otro, de manera que
coincidan las comas decimales.
La cantidad de cifras decimales
debe ser la misma. Luego, se
procede a sumar.
¿Cómo se
realiza la adición
y sustracción
de números
decimales?

79. INGENIO
L U D O M A T I C
Aritmética
79
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Ximena desea comprar los siguientes
objetos. Determina cuánto pagará por
ellos. Comunica tu respuesta.
S/. 5,82 S/. 3,61 S/. 1,33
Resolución:
a) Sabemos que:
= S/. 5,82
S/. 3,61
S/. 1,33
=
=
b)
Efectuamos la operación de adición.
5,82 +
3,61
1,33
10,76
c) Comunicamos la respuesta.
Se pagará S/. 10,76
Relaciona las operaciones y respuestas
de cada columna según corresponda.
Argumenta tu respuesta.
18,6 + 77,4 + 23,4 13,26
196,1
119,4
17,5 – 4,24
(112,8 + 206,5) – 123,2
Resolución:
Efectuamos las operaciones.
18,6 +
77,4
23,4
119,4
112,8 +
206,5
319,3
319,3 –
123,2
196,1
17,50 –
4,24
13,26
Entonces:
18,6 + 77,4 + 23,4 13,26
196,1
119,4
17,5 – 4,24
(112,8 + 206,5) – 123,2
Resuelve las siguientes adiciones y
sustracciones:
a)
142,124 – 63,23
b)
781,01 + 162,82
Resolución:
a)
Escribimos los números
verticalmente.
1 4 2, 1 2 4
6 3, 2 3 0
7 8, 8 9 4
-
b)
+
7 8 1, 0 1
1 6 2, 8 2
9 4 3, 8 3
Alessandra compró una tablet en
S/. 202,99. Si la vende, ganando
S/. 23,01, ¿en cuánto vendió la tablet?
Resolución:
a)
Sabemos que:
Precio de compra = S/. 202,99
Ganancia = S/. 23,01
Precio de venta = x
b)
Efectuamos las operaciones.
202,99 +
23,01
226,00
c) Comunicamos la respuesta.
Alessandra vendió la tablet en
S/. 226,00.

80. INGENIO
4.° primaria
L U D O M A T I C
80
I)
II)
I)
II)
a)
b)
a)
b)
Indicadores de evaluación
Calculo la adición de números decimales.
Determino la sustracción de números decimales.
Desarrollo problemas con operaciones combinadas
de números decimales.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
8 5 27 6 5 9 3 7
3
10
, , , ,
+ −
( )

 
 + −







81. NÚMEROS DECIMALES
PROYECTO DE APRENDIZAJE N.0
6
INGENIO
1. Situación problemática
Medir es parte importante de la actividad humana. Se necesita conocer la estatura, el
peso, la distancia que recorremos, la temperatura, etc. Esto le permite al hombre conocer
mejor su entorno, determinar las características que presenta y tomar las decisiones
adecuadas. Estas medidas se presentan muchas veces con números decimales que
son necesarios conocer.
2. Finalidad
Que los estudiantes utilicen los números decimales para determinar la estatura de los
alumnos del 4.° grado.
3. Recursos materiales
Cinta. Hojas bond.
Borrador. Lápices.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de 4
estudiantes.
Elaboran una tabla
donde se registrará
los nombres de los
estudiantes y su estatura.
Miden la estatura de los
estudiantes del salón.
Ordenan esta
información en un
cuadro.
Identifican la mayor y
menor estatura.
Interpretan
el cuadro y
exponen.
81

82. UNIDAD
7
Cultivamos Valores
•
Educación para
la equidad de
géneros.
• Tolerancia.
Aprendemos a
•
Reconocer y utilizar las unidades de
tiempo.
•
Utilizar equivalencias y canjes con
monedas y billetes.
•
Resolver operaciones de referentes
temporales.
Observa la imagen y contesta.
¿Sabes qué es la igualdad de géneros?
¿Hombres y mujeres tienen las mismas oportunidades?
REFERENTES
TEMPORALES
Educación en equidad de géneros

83. INGENIO 83
1. Formamos equipos de cuatro (4) integrantes.
2.
Cada grupo, traerá una cartulina y la dividirá
en dos columnas y 12 filas; luego, pegarán la
cartulina en la pizarra.
1. Cada grupo cortará 24 tiras de papel en las
que escribirá los meses del año y las siguientes
festividades:
- Navidad.
- Año nuevo.
- Fiestas patrias.
- Inicio de clases.
- Día de la primavera.
- Señor de los Milagros.
- Día de la bandera.
- Día de la madre.
- Carnavales.
- Día del idioma.
- Santa Rosa de Lima.
- Inicio de clases.
2. Deberán ubicar los meses del año en la primera
columna de forma ordenada.
3. Luego, deberán elegir la festividad
correspondiente a cada mes del año y pegarla.
4. Gana el equipo que termine primero.
J U G A N D O C O N
L O S M E S E S
Nos organizamos
Jugamos y aprendemos
7
LABORATORIO

84. INGENIO
84
REFERENTES
TEMPORALES
UNIDADES DE TIEMPO
La unidad principal del tiempo es el segundo y el mecanismo utilizado para su medida
es el reloj.
Por lo tanto:
La tercera sirena se toca a las 8 y 45 de la mañana o a las 8: 45 a.m.
La primera
sirena se
toca a las…
La segunda
s i r e n a s e
toca a las…
La tercera
s i r e n a s e
toca a las…
1 hora tiene 3600 segundos.
1 hora tiene 60 minutos.
1 minuto tiene 60 segundos.
1
2
3
12
11
10
6 5
4
9
8
7
1 1 1
2 2 2
3 3 3
12 12 12
11 11 11
10 10 10
6 6 6
5 5 5
4 4 4
9 9 9
8 8 8
7 7 7
Reloj
8 : 15 a. m.
De nuestro ejemplo:
8 : 30 a. m. 8 : 45 a. m.
TALLER
16
Es una magnitud que
mide la duración de
las cosas.
¿Qué es la unidad
de tiempo?
En mi colegio, la hora de
entrada es a las 8:00 am
y cada 15 minutos se
toca la sirena.
¿A qué hora toca
la tercera sirena?

85. INGENIO
L U D O M A T I C
Aritmética
85
El día
Es el tiempo que tarda la tierra en dar una vuelta sobre su eje; es decir, 24 horas.
La semana
Es un periodo de tiempo de 7 días. 1 semana = 7 días
Los días de la semana son lunes, martes, miércoles, jueves, viernes, sábado y domingo.
Ejemplo:
1. ¿Cuántos días hay en 3 semanas?
Resolución:
3 semanas = 3 × 7 = 21 días
El año
Un año tiene 12 meses. 1 año = 12 meses
Los meses del año son
Enero
Julio
Febrero
Agosto
Marzo
Septiembre
Abril
Octubre
Mayo
Noviembre
Junio
Diciembre
Ejemplos:
1. ¿Cuántos meses hay en 5 años?
Resolución:
5 años = 5 × 12 meses = 60 meses
Antes del mediodía
Desde las 12 de la noche hasta las 12
del mediodía, se lee las horas como
aparecen o se agrega las siglas am
(antes meridiano)
Las 8 de la mañana o 8 a.m. Las 13 horas o 1 de la
tarde (1: 00 p.m.)
Desde las 12 del mediodía hasta las 12 de
la noche, se lee las horas como señala el
reloj o se agrega las siglas pm (pasado
meridiano).
Después del mediodía
24 horas = 1 día
08 : 00 13 : 00
2. ¿Cuántos semanas hay en 35 días?
Resolución:
35 días = 35 ÷ 7 = 5 semanas
Ejemplos:
1. ¿Cuántos años hay en 4 décadas?
Resolución:
4 décadas = 4 × 10 años = 40 años
2. ¿Cuántos años hay en 48 meses?
Resolución:
48 meses = 48 ÷ 12 años = 4 años
2. ¿Cuántos meses hay en 3 trimestres?
Resolución:
3 trimestres = 3 × 3 = 9 meses
Otras unidades de tiempo
Entre estas unidades tenemos las siguientes:
1
2
3
12
11
10
6 5
4
9
8
7
1
2
3
12
11
10
6 5
4
9
8
7
1 lustro = 5 años
1 década = 10 años
1 siglo = 100 años
1 bimestre = 2 meses
1 trimestre = 3 meses
1 semestre = 6 meses
2015
2015

86. INGENIO
4.° primaria
L U D O M A T I C
86
1 2
ANALIZAMOS Y APRENDEMOS
Álvaro fue al cine a ver la película
“Piratas del Caribe”, que tuvo una
duración de una hora y 20 minutos.
Determina cuántos segundos duró la
película. Comunica tu respuesta.
Resolución:
a) La película duró 1 hora 20 minutos.
b) Convertimos la hora a segundos.
1 h = 3 600 segundos.
c)
Convertimos los 20 minutos a
segundos.
20 minutos = 20 × 60 segundos =
1 200 segundos
d)
La película dura en total:
1 hora 20 minutos = 3 600 + 1 200 segundos
= 4 800 segundos
e)
Por lo tanto, la película dura en total
4 800 segundos.
Relaciona, mediante líneas de color, las
festividadesconsumescorrespondiente.
-
-
-
Navidad
Fiestas patrias
Batalla de Arica
Julio
Junio
Diciembre
Resolución:
a) Sabemos que:
-LaNavidadsecelebraendiciembre.
- Fiestas patrias se celebra en julio.
-
La batalla de Arica se conmemora
en junio.
Entonces:
Navidad
Fiestas patrias
Batalla de Arica
Julio
Junio
Diciembre
3.
Pasé 4 horas en una excursión y
320 minutos en clases. Determina en qué
actividad pasé más tiempo. Elabora una
estrategia de solución.
Resolución:
a) Comprendemos el problema.
Para comparar los tiempos debemos
usar una misma unidad, en este caso
nos conviene los minutos.
b) Efectuamos operaciones.
i)
Pasando a minutos el tiempo
empleado en la excursión.
4 horas = 4 × 60 min
60 min = 240 min
ii)
El tiempo que pasa en clases es 320
minutos.
iii) Comparamos los tiempos.
320 min 240 min
clases excursión
c)
Comunicamos la respuesta.
Por lo tanto, pasa más tiempo en
escuchar clases
4.
Determina el valor de verdad de las
siguientes proposiciones:
I.
Media hora equivale a 15 minutos.
( )
II.
En un día hay 1 440 minutos. ( )
III.
Una semana equivale a 160 horas.
( )
Resolución:
a) Analizamos cada proposición:
I. Falso; 1 hora = 60 minutos.
1
2
hora = 30 minutos.
II. Verdad: 1 día = 24 horas, 1h = 60 min.
Þ 1 día = 24 (60) = 1 440 minutos.
III.
Falso: 1 semana = 7 días, 1 día = 24
horas.
Þ 1 semana = 7(24) = 168 horas.
b) Los valores de verdad son FVF.
3 4

87. INGENIO
L U D O M A T I C
Aritmética
87
Indicadores de evaluación
Convierto horas a minutos y segundos.
Identifico los meses del año.
Resuelvo problemas con unidades de tiempo.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
1
2
3
12
11
10
6 5
4
9
8
7

88. INGENIO
88
EQUIVALENCIAS Y CANJES
CON MONEDAS Y BILLETES
SISTEMA MONETARIO PERUANO
De nuestro ejemplo:
Sumamos los precios de la gaseosa y la galleta.
Por lo tanto, me deben dar vuelto 1 Nuevo Sol y 70 céntimos.
La cantidad de dinero que tengo es 2 + 2 +1 + 1 + 1= S/. 7
Me deben dar de vuelto la diferencia entre lo que tengo y lo que cuesta la gaseosa y
la galleta; es decir:
Lo que tengo
Lo que cuesta la galleta y la gaseosa
Cara Sello
3 soles y
50 céntimos (S/. 3,50)
1 Nuevo Sol y 80
céntimos (S/. 1,80)
3,50 +
1,80
7,00 –
5,30
5,30
1,70
S/.
S/.
TALLER
17
Se desea comprar un
litro de gaseosa y un
paquete de galleta,
cuyos precios se
indican en la figura.
Si tengo estas
monedas, ¿cuánto
de vuelto me
deben dar?
¿Cuál es
la unidad
monetaria
del Perú?
Desde el 1.° de
julio de 1991, es
el Nuevo Sol y su
símbolo es S/.

89. INGENIO
L U D O M A T I C
Aritmética
89
3 soles y
50 céntimos
(S/. 3,50)
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Álvaro tiene un billete de S/. 50 y debe
comprar los siguientes productos.
S/. 5,20 S/. 3,40
S/. 4
Determina cuánto de vuelto recibirá. Luego,
elabora tu estrategia de solución.
Resolución:
a)
Determinamos el costo total de la compra.
S/. 5,20 +
S/.12,60
Arroz
Azúcar
Leche
S/. 4,00
S/. 3,40
b)
Determinamos el vuelto:
c)
Por lo tanto, recibe de vuelto S/. 37,40.
Relaciona, mediante flechas, las
cantidades monetarias de las columnas.
Comunica tu respuesta.
Resolución:
a)
Comparamos las cantidades de las
columnas.
=
=
b)
Relacionamos mediante flechas.
Cantidad que paga.
Vuelto
50,00
50 –
S/.37,40
12,60
12,60 Costo de la compra.
S/. 278 =
=
S/. 341
Relaciona correctamente el valor de los
objetos mediante flechas.
Resolución:
a)
Comparamos las cantidades de las columnas.
S/. 278
S/. 341
b) Entonces:
Alessandra va a comprar una secadora de cabello
que cuesta S/. 250. Si para pagar lleva un billete de
100 Nuevos Soles, 2 billetes de 50 Nuevos Soles, 1 billete
de 20 Nuevos Soles, un billete de 10 Nuevos Soles, una
moneda de 5 Nuevos Soles y 2 monedas de 2 Nuevos
Soles; ¿le alcanzará para comprar la secadora?
Argumenta tu respuesta.
Resolución:
a)
Determinamos la cantidad de dinero que
tiene Alessandra.
S/. 100
S/. 239
S/. 50
S/.50
S/.20
S/.10
S/.5
S/.2
S/.2
Alessandra tiene
b)
Como el precio de la secadora es mayor,
tenemos la siguiente expresión:
250 – 239 = 11
c)
Por lo tanto, le faltará S/. 11.
S/. 278
S/. 341

90. INGENIO
4.° primaria
L U D O M A T I C
90
4.
4.
Indicadores de evaluación
Realizo operaciones de cambio de monedas.
Establezco equivalencias monetarias.
Resuelvo problemas empleando billetes y monedas.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
S/. 226 S/. 550 S/. 240

91. PROYECTO DE APRENDIZAJE N.0
7
INGENIO
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1. Situación problemática
Todos los países del mundo tienen un sistema monetario que le permite manejar la
economía. En este sistema, hay billetes y monedas. Es importante conocer cuál es la
unidad de dicho sistema; por ejemplo en el Perú es el Nuevo Sol (S/.), en EEUU es el dólar
($), etc. Es necesario conocer el tipo de cambio para poder establecer la equivalencia
entre una moneda y otra.
2. Finalidad
Que los estudiantes conozcan la equivalencia entre Nuevos Soles y dólares; además
de manejar el tipo de cambio.
3. Recursos materiales
Catálogos y revistas. Hojas bond.
Borrador. Lápices.
Regla.
4. Etapas y actividades
5. Evaluación
REFERENTES TEMPORALES
1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos
de cuatro (4)
estudiantes.
Traen catálogos y
revistas de artefactos
en donde los precios
estén en dólares.
Averiguan el tipo de cambio del
dólar del día y de hace un mes.
Conviertenamonedanacionalel
precio de 5 artículos o artefactos.
Determinan cuál ha sido el
aumento o disminución del
precio y exponen.
Pegan y
exponen
sus
trabajos.
91

92. Cultivamos valores
•
Educación para el
éxito.
• Responsabilidad.
ESTADÍSTICA
Aprendemos a:
•
Ordenar y representar cuadros de doble
entrada.
•
Representar los datos en gráficos de línea
y pictogramas.
Observa la imagen y contesta.
¿Qué actitudes crees que debes tener para lograr el éxito?
¿Cómo te considerarías al finalizar la etapa escolar?
Educación para el éxito
UNIDAD
8

93. INGENIO
L U D O M A T I C
Aritmética
93
Cada equipo elaborará el cuadro que se
muestra en la cartulina, (fig. 1). Luego, se
procederá de la siguiente forma:
1. Cada integrante lanzará los dados juntos.
2. Si los resultados son los siguientes:
• Dos números pares: 8 puntos.
• Dos números impares: 10 puntos.
• Un par y un impar: 5 puntos.
3. Estos resultados los colocan en el cuadro.
4. Cada integrante lanzará los dados en 3
oportunidades.
5. Se suma todos los puntajes de todos los
integrantes.
J U G A N D O C O N
L O S D A D O S
Nos organizamos
Jugamos y aprendemos
Gana el equipo que
obtuvo mayor puntaje.
En caso de empate, se
lanzará una moneda.
1. Forman equipos de cuatro (4) integrantes.
2. Cada equipo traerá una cartulina y 2
dados.
Nombre
Lanzamientos
1.° 2.° 3.°
Total
Fig. 1
8
LABORATORIO

94. INGENIO
94
fruta Cantidad (kg)
6
10
4
10
CUADRO DE DOBLE ENTRADA
Y GRÁFICO DE BARRAS
CUADRO DE DOBLE ENTRADA
GRÁFICO DE BARRAS
Frutas Cantidad
manzana 6 kg
naranja 10 kg
piña 4 kg
fresa 10 kg
De nuestro ejemplo, se tiene la siguiente cantidad de frutas:
Estos datos los podemos ordenar y representar en un cuadro de doble entrada.
Representamos la información
en un gráfico de barras.
Manzana = (6)
Naranja = (10)
manzana naranja piña fresa
frutas
Cantidad
12
11
10
9
8
7
6
5
4
3
2
1
TALLER
18
Hoy debemos ir a
comprar fruta.
¿Qué es un cuadro
de doble entrada?
Es una tabla donde
registramos los datos
que se presentan.
Piña = (4)
Fresa = (10)

95. INGENIO
L U D O M A T I C
Aritmética
95
3. Elabora un gráfico de barra para registrar la
cantidad de canicas que tienen los niños.
Resolución:
a)
Contamos el número de canicas que tiene
cada niño y lo registramos en el cuadro de
doble entrada.
b) Elaboramos el diagrama de barras.
El puntaje obtenido por las secciones
de 4.° grado, en las últimas olimpiadas
escolares, es registrado en el siguiente
gráfico de barras. Elabora su tabla de
doble entrada.
Resolución:
a)
Elaboramos el cuadro de doble entrada.
En la primera columna, colocamos las
secciones y, en la segunda, el puntaje
obtenido por cada una de ellas.
Álvaro Sebastián Ricardo Abel
niños
Cantidad
de canicas
10
9
8
7
6
5
4
3
2
1
1 2
3 4
ANALIZAMOS Y APRENDEMOS
La cantidad de personas de un colegio, entre
alumnos y profesores, mostrada en el gráfico
de barras. Determina el valor de verdad de
las siguientes proposiciones, argumentando
tu respuesta.
Resolución:
a) Analizando las proposiciones:
I) Falso: porque:
niños + niñas = 90 + 80 = 170
II)
Verdadero: porque:
profesores + alumnos = 170 + 20 = 190
III)
Verdadero: el gráfico muestra 90 niños.
La tabla muestra la venta de varios meses:
Elabora su diagrama de barra y responde:
a)¿En qué mes se vendió más televisores?
b)¿
Cuántos televisores más se vendió en
setiembre con respecto a agosto?
Resolución:
Realizamos el diagrama de barras,
trasladando la información al cuadro.
Junio Julio Agosto Setiembre
meses
50
30
20
28
Cantidad
de TV
Respondemos utilizando el gráfico
a)
En el mes de julio, se vendió más
televisores(50).
b)
En setiembre, se vendió 28 televisores.
c) En agosto, se vendió 20 televisores.
d) Entonces: 28 – 20 = 8
En setiembre se vendió 8 televisores
más con respecto al mes de agosto.
Mes N° de T.V vendidos
Junio 30
Julio 50
Agosto 20
Setiembre 28
I) El número de alumnos es 180.
II) El número de personas es 190.
III) La cantidad de niños es 90.
Niñas
Cantidad
Miembros
Niños Profesores
90
80
70
60
50
40
30
20
10
Niños Cantidad
Álvaro 10
Sebastián 7
Ricardo 9
Abel 6
4.° A 4.° B 4.° C
Secciones
Puntaje Olimpiadas escolares
40
35
30
25
4.° Puntaje
A 25
B 40
C 35
Álvaro
10
Sebastián
7
Ricardo
9
Abel
6

96. INGENIO
4.° primaria
L U D O M A T I C
96
Indicadores de evaluación
Represento cuadros de doble entrada.
Reconozco un gráfico de barras.
Construyo cuadros de doble entrada y gráfico de barras.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Elabora un cuadro de doble entrada
y registra en él los diferentes objetos
mostrados con sus cantidades.
Comunica tu respuesta.
Relaciona las dos columnas de
acuerdo al gráfico.
El gráfico muestra la asistencia de los
estudiantes en el 1er
trimestre de clases.
Indica la veracidad de las siguientes
proposiciones,argumentandoturespuesta.
I)
En el 1er
mes, la asistencia fue mayor.
II)
En el mes de abril, las inasistencias
fueron mayores.
III)
Si los alumnos del salón son 35; en
mayo faltarán 5.
El cuadro muestra el consumo de
kilos de pollo por familia en Lima.
Elabora el gráfico de barras y
responde:
a)¿En qué mes se consumió más
pollo?
b)¿
En qué mes se consumió menos
pollo?
Lunes gastó
Martes gastó
Gastó menos el
Miércoles
S/. 25
S/. 35
Lunes Martes Miércoles Jueves
Día
Cantidad
35
30
25
20
15
10
5
Marzo Abril Mayo
Meses
N.° de alumnos
35
30
25
20
Mes Kg
Abril 20
Mayo 40
Junio 35
Julio 38
Agosto 32

97. INGENIO 97
GRÁFICO LINEAL
El diagrama de barras lo podemos representar de la siguiente forma:
¿Habrá otras formas
gráficas de representar
esta tabla?
5
10
15
20
25
30
Días
Días
Nº alumnos
Nº alumnos
Asistencia
5
10
15
20
25
30
Lu. Ma. Mi. Ju. Vi.
Asistencia
Las alturas de las barras las
representamos con puntos.
Ahora unimos los puntos con una línea recta.
Esta representación
gráfica se conoce
como Gráfico lineal.
Lu.
5
10
15
20
25
30
Ma.
Días
Ju. Vi.
Mi.
N.º Alumnos
• El gráfico nos muestra la asistencia de los alumnos.
GRÁFICO DE LÍNEAS
Y PICTOGRAMA
En el gráfico de
barras, se registra la
asistencia a clases
de 4.° grado durante
una semana.
Lu. Ma. Mi. Ju. Vi.
TALLER
19

98. INGENIO
4.° primaria
L U D O M A T I C
98
PICTOGRAMA
Es un diagrama que emplea dibujos para mostrar datos de una forma rápida.
Ejemplo 1
El siguiente pictograma se registra la cantidad de árboles sembrados en los 4 prime-
ros meses del año.
Con los datos del Pictograma, podemos interpretar lo siguiente:
En Enero, se ha sembrado: 6 x 4 = 24 árboles.
En Febrero, se ha sembrado: 5 x 4 = 20 árboles.
Ejemplo 2
Según el pictograma mostrado:
Determina la cantidad de estampitas obtenidas por los niños y responde quién de
ellos obtiene más estampitas.
Solución:
i) Alessandra = 3
Telassim = 1
Juan = 5
Álvaro = 4
Ximena = 2
Total =15
Mes Recuento
Enero
Febrero
Marzo
Abril
= 4 árboles
ii) De acuerdo al gráfico:
Juan tiene más estampitas (5).
Alumno N.º de estampitas
Alessandra
Telassim
Juan
Álvaro
Ximena

99. INGENIO
L U D O M A T I C
Aritmética
99
1.
Dado el gráfico lineal, determina el valor de
verdad de las siguientes proposiciones.
I) El total de alumnos de 4.° grado es 90. ( )
II)
El número de alumnos del 4.° A es ( )
igual al de 4.° D.
III) El aula con menos alumnos es el 4.° B. ( )
Resolución:
I) Falso, porque 4.° A = 25 alumnos
4.° B = 20 alumnos
4.° C = 30 alumnos
4.° D = 25 alumnos
Total = 100 alumnos
II)
Verdad, 4.° A - 25 alumnos y 4.° D = 25
alumnos.
III)
Verdad, 4.° B = 20 alumnos es el aula con
menos alumnos.
pastel
Cantidad
4
3
2
1
Selva Fresa Chocolate Lúcuma
Negra
Dado el cuadro, elabora un pictograma
donde cada gráfico vale 5 unidades.
Artefacto TV Laptop Tablet USB
Cantidad
vendida
15 15
20 10
Responde:
¿Cuál es la diferencia entre el número de
televisores y el número de tablets?
Resolución:
a) Elaboramos el pictograma.
b) Respondemos la pregunta:
Número de televisores = 20
Número de tablets = 15
La diferencia es 20 - 15 = 5.
El gráfico lineal indica las edades de los
integrantes de una familia. Completa el
cuadro con la información adecuada.
Resolución:
a)
Del gráfico, podemos determinar que:
la mamá tiene 30 años.
el papá tiene 35 años.
Álvaro tiene 10 años.
Alessandra tiene 5 años.
b)
Completamos el cuadro.
El pictograma muestra el número de
pasteles que ha preparado Telassim para
su fiesta. Elabora el diagrama lineal.
Resolución:
a) Determinamos la cantidad de pasteles.
Selva negra = 3 Fresa = 1
Chocolate = 4 Lúcuma = 2
b) Elaboramos el gráfico lineal:
Tipo de pastel Cantidad
Selva negra
Fresa
Chocolate
Lúcuma
1 2
3 4
ANALIZAMOS Y APRENDEMOS
4.° grado
N.º Alumnos
35
25
20
15
10
5
4.° A 4.° B 4.° C 4.° D
Cantidad de artefactos
Artefacto
TV
Laptop
Tablet
USB
Parientes
Años
35
30
25
20
15
10
5
Mamá Papá Alvaro Alessandra
Edad
Mamá
Papá
Álvaro
Alessandra
Edad
Mamá 30
Papá 35
Álvaro 10
Alessandra 5

100. INGENIO
4.° primaria
L U D O M A T I C
100
Indicadores de evaluación
Elaboro gráficos de barras y lineales.
Reconozco la información que brinda un gráfico.
Construyo una tabla con la información de los gráficos.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
El gráfico muestra el número de
alumnos por nivel de un colegio.
Completa el cuadro.
Nivel N.º de Alumnos
Inicial
Primaria
Secundaria
180
150
120
40
60
30
Inicial Primaria Secundaria
N.º Alumnos
Nivel
Elabora un pictograma con la
siguiente información sobre la
cantidad de jóvenes que usamos
camisa, polo y chompa en un
salón.
Elabora un gráfico lineal con la
siguiente información.
¿Quién es mayor?
¿Quién es menor?
Niño Álvaro Sebastian Alessandra Ximena
Edad 12 11 7 14
En el gráfico lineal, se registra los goles
anotados en las 4 primeras fechas
del campeonato escolar. Elabora un
pictograma.
10
8
6
4
2
1.er
Fecha
3.er
Fecha
2.o
Fecha
4.o
Fecha
Nº de goles
Fechas
Camisa 10 alumnos
Polo 20 alumnos
Chompa 15 alumnos

101. INGENIO 101
P(evento Imposible)= O
PROBABILIDAD
El árbitro de fútbol
siempre lanza una
moneda para
determinar quién
inicia el juego.
¿Qué es la
Probabilidad?
La probabilidad del evento A, se representa P(A) y se determina como:
Número de casos favorables de A
Número total de casos posibles
P(A) =
Veamos:
Si lanzamos una moneda, existen 2 opciones o casos posibles.
Evento A = Obtener cara
1
2
La probabilidad de obtener cara en un lanzamiento es
P(A) = Probabilidad de obtener cara.
Número de casos que salga cara
Número de casos posibles
P(A) =
=
1
2
1
2
P(A)=
Evento imposible
No posee ningún caso favorable.
Ejemplo: al lanzar un dado se obtiene 12.
Evento Seguro
Todos los casos son favorables.
Ejemplo: al lanzar una moneda se obtenga sello o cara.
P(evento Seguro)= 1
CARA
1.a
opción
o caso
SELLO
2.a
opción
o caso
PROBABILIDADES
Asi es; solo
se tiene dos
probabilidades
cara o sello.
Es la razón del número de
casos favorables entre el
total de casos posibles.
TALLER
20

102. INGENIO
4.° primaria
L U D O M A T I C
102
3.
En una caja, se tiene 6 esferas de
color rojo y 4 de color negro. ¿Cuál
es la probabilidad de que, al extraer
una esfera, ésta sea roja? Elabora una
estrategia de solución.
Resolución:
a)
Comprendemos el problema.
Se tiene:
b) Calculamos la probabilidad.
Evento A = Salga una esfera roja.
P(A)=
P(A)= = 0,6
c)
Comunicamos la respuesta.
Por lo tanto, la probabilidad de sacar
una esfera roja es de 0,6.
1.
Luego de lanzar un dado, determina la
probabilidad de obtener 4. Argumenta
tu respuesta.
Resolución:
Graficamos los casos posibles.
a)
Al lanzar un dado se tiene 6 casos
posibles.
Calculamos la probabilidad.
b) Sea el evento A = obtener 4
P(A) =
P(A) =
Comunicamos la respuesta.
c)
Por lo tanto, la probabilidad que
salga 4 es de
1
6
1
6
Número de casos que salga 4
Número total de caso
6
10
Total de esferas = 10
Número de casos que salgan 2 sellos
Número total de casos
4.
Se lanza una moneda dos veces
consecutivas.Determinalaprobabilidad
de obtener sello dos veces. Elabora una
estrategia de solución.
Resolución:
a) Sabemos que:
1.er
Lanzamiento puede salir
2.° Lanzamiento puede salir
b)
Ahora, usamos el diagrama del árbol.
Evento A = obtener 2 sellos.
P(A)=
c)
Luego, la probabilidad de obtener
2 sellos es
Cara (c)
Cara (c)
Sello (s)
Sello (s)
1.er
Lanzamiento
C
S
2.o
Lanzamiento
C
S
C
S
Resultado
C C
C S
S C
S S
}Son
4 casos
1
4
=
1
4
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Determina el valor de verdad de las
siguientes proposiciones, argumentando
tu respuesta.
I) La probabilidad de obtener cara al
lanzar una moneda es ( )
II)
La probabilidad de obtener 8 al
lanzar un dado es ( )
III)
Al lanzar un dado, la probabilidad de
obtener números desde 1 a 6 es 1. ( )
Resolución:
a) Analizando cada caso.
I)
Verdadero: al lanzar una moneda
la probabilidad que resulte es
II)
Falso: al lanzar un dado solo se
puede obtener valores hasta 6.
P(7) = 0
III)
Verdadero: es un caso de evento
seguro P(E) = 1
1
6
1
2
1
2
Número de casos que salga roja
Número de casos totales

103. INGENIO
L U D O M A T I C
Aritmética
103
3 4
EnelsalóndeAlessandra,hay20niñas
y 10 niños. Si se elige un delegado del
aula, ¿cuál es la probabilidad que
sea niña?
Elabora una estrategia de solución.
Se tiene los siguientes eventos:
A = Un número par que termine en 5.
B =
Lanzar un dado y obtener un
número impar.
C =
Encontrarunleónqueseamamífero.
Relacionacorrectamentelascolumnas.
Argumenta tu respuesta.
Indicadores de evaluación
Calculo la probabilidad que ocurra en evento.
Reconozco los eventos imposibles y seguros.
Resuelvo problemas relacionados con probabilidades.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
2
¿
Cuál es la probabilidad que, al lanzar
un dado, se obtenga un número par?
Elabora una estrategia de solución.
Se organiza un campeonato de
fulbito con las secciones A, B y C de
3.er
, 4.o
y 5.o
de secundaria. Indica
cuál es la probabilidad que:
a)
El campeón pertenezca a la
sección B.
b) El campeón pertenezca a 4.o
A.
c)
El campeón sea un salón de 5.o
grado.
Argumenta tu respuesta.
1
0
1
2
P(A)
P(B)
P(C)

104. PROYECTO DE APRENDIZAJE N.0
8
INGENIO
ESTADÍSTICA
1. Situación problemática
En la vida diaria, es necesario conocer cómo es la evolución de ciertas actividades
que realizamos; por ejemplo: consumo de agua, nuestra talla, nuestro peso, etc.
Estas situaciones pueden ser representadas gráficamente para que su análisis e
interpretación sean más sencillos.
2. Finalidad
•
Elaborar, representar e interpretar gráficos estadísticos que muestran situaciones
relacionadas con actividades diarias.
• Reconocer la importancia de los gráficos estadísticos.
3. Recursos materiales
Recibo de agua. Hojas bond.
Borrador. Lápices.
Regla.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
5. Evaluación
1.ª etapa 2.ª etapa 3.ª etapa
Formamos grupos de 4
estudiantes.
Eligen un recibo
de algunos de los
estudiantes.
Eligen los últimos 4
meses para analizar.
Presentan, en un cuadro de
doble entrada, el consumo
de los últimos 4 meses.
Representan esta información
en un gráfico de barras y en
un diagrama lineal.
Interpretan cuál ha sido la
evolución del consumo de
agua.
Exponen
y explican
los trabajos
realizados.
104

105. Observa la imagen y contesta
UNIDAD
1
Reciclar es amar al planeta
¿Sabes qué es reciclar?
¿Qué formas de reciclaje conoces?
¿Qué podemos hacer para preservar nuestro planeta?
Aprendemos a:
Cultivamos valores
• Educación para la
concienciaambiental.
•
Responsabilidad.
•
Identificar los elementos de la potenciación
y la radicación.
• Aplicar las propiedades de la potenciación.
• Reconocer la relación entre los elementos
de la potenciación y radicación.
• Resolver problemas de diferentes contextos
que impliquen el uso de la potenciación
y la radicación.

106. 4.° primaria
L U D O M A T I C
INGENIO
106
Jugamos y Aprendemos
Nos organizamos
FORMAMOS
CUADRADOS
LABORATORIO
1
1. Forma equipos de 4 integrantes.
2. Cada integrante debe traer una cartulina de
color y una tijera.
3. Los integrantes de cada equipo recortarán
sus cartulinas en tarjetas cuadradas como
muestra la figura. (Ver Fig. 1).
1. Colocar las tarjetas recortadas sobre la
mesa de trabajo y los equipos se disponen a
comenzar el juego.
2.
Cada equipo empleará sus tarjetas: para ello,
deben resolver los siguientes problemas:
Problema 1.
Formen un cuadrado compacto,
colocando 4 tarjetas por lado.
Problema 2. Si han empleado 25 tarjetas
paraformaruncuadradocompacto,¿cuántas
tarjetas hay en cada lado?
Problema 3. Con 30 tarjetas formen el mayor
cuadrado compacto posible. ¿Cuántas tarje-
tas sobran?
Problema 4. Con 45 tarjetas, formen un
cuadrado compacto. ¿Cuántas tarjetas
debe agregarse como mínimo para lograrlo?
3. Ganará el equipo que tenga la mayor cantidad
de aciertos en el menor tiempo posible.
5 cm
5 cm
Fig. 1

107. L U D O M A T I C
INGENIO
Álgebra
107
NOCIÓN DE POTENCIACIÓN
Ejemplos:
Ejemplos:
■ 103
= 10 × 10 × 10 = 1000
Lectura y escritura de la potenciación
■ 52
se lee “cinco al cuadrado”.
■ 25
se lee “dos elevado al exponente cinco”.
■ 34
se lee “tres elevado al exponente cuatro”.
■ 52
= 5 × 5 = 25
}
2 veces
4
4
4
POTENCIACIÓN
Mi cubo está formado por
3 cubitos de largo, 3 de an-
cho y 3 de alto. El total de
cubitos que lo forman es:
3 × 3 × 3 = 27
Y mi cubo,
¿por cuántos cubitos
estará formado?
¿Qué es la
potenciación?
■
De nuestro ejemplo, tenemos que la
cantidad de cubitos del segundo cubo es ...
4 × 4 × 4 = 64
“3 veces”
Esta expresión puede representarse
como: 43
= 64 y se llama potenciación.
ELEMENTOS DE LA POTENCIACIÓN
}
Es la operación que hace que un
número llamado base se multiplique
tantas veces como lo indique otro
llamado exponente y dé como resultado
un número llamado potencia.
4 = 4 ×4 × 4 = 64 Potencia
3
3 veces
Exponente
Base
}
1
TALLER

108. 4.° primaria
L U D O M A T I C
INGENIO
108
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Si:
Determinaelvalordeverdaddelassiguientes
proposiciones y argumenta tu respuesta:
I. 2 es el exponente.
II. 4 es la base.
III. 16 es la potencia.
Resolución:
a) Identificamos los elementos de la
potenciación.
b) Determinamos el valor de verdad de las
proposiciones.
I. Es falso: 2 es la base.
II. Es falso: 4 es el exponente.
III. Es verdadero: 16 es la potencia.
c) Los valores de verdad son FFV.
24
= 2 × 2 × 2 × 2 = 16
24
= 2 × 2 × 2 × 2 = 16
exponente
base
potencia
4 veces
Resolución:
a) Completamos las potenciaciones.
Completa los espacios para obtener
las potenciaciones correctas.
● 4 = 64
● = 81
● 62
=
2
b) Se completa con los números: 3 ; 9 y 36.
Expresa la cantidad de cubitos de la
figura como una potenciación.
Resolución:
a) Observamos que la figura tiene 5
cubitos por lado.
b) El total de cubitos que lo forman es...
c) Expresamos como potenciación:
5 × 5 × 5 = 125
}
3 veces
}
3 veces
5 × 5 × 5 = 53
5
5
5
En un almacén, hay una pila de
cajas de zapatos que tienen 4 cajas
en el largo, 4 en el ancho y 4 en el
alto. Si cada caja se vende en S/. 30,
¿cuánto cuesta la pila? Elabora tu
estrategia de solución.
Resolución:
a) Graficamos el problema:
b) Analizamos el problema.
● La cantidad de cajas de
zapatos que se tiene es…
4 × 4 × 4 = 43
= 64.
● En 64 cajas a 30 soles, se tiene
64 × 30 = 1 920.
c) Por lo tanto, la pila de zapatos
cuesta S/. 1 920.
}
}
}
3 veces
2 veces
2 veces
3
2
● 4 = 4 × 4 × 4 = 64
● 9 = 9 × 9 = 81
● 62
= 6 × 6 = 36

109. L U D O M A T I C
INGENIO
Álgebra
109
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Identifico los elementos de una potenciación.
Calculo el valor de una operación con potenciación.
Completo los elementos que faltaban en una
potenciación.
Resuelvo problemas con potenciación.
Determina el valor de las siguientes
operaciones y compara tu respuesta
con la de tus compañeros.
● A = 32
+ 42
+ 52
● B = 102
– 92
● C = (1 + 2 + 3)2
– 12
– 32
● D = 23
+ 32
+ 43
+ 34
Expresa la cantidad de ladrillos que
hay en la pared en forma de poten-
ciación.
¿Cuántas aves como mínimo hacen
falta para que haya un número
cuadrado de ellas? Elabora una
estrategia de solución.
Determina cuántos cuadraditos hay en
la figura 6 de la secuencia mostrada.
Elabora una estrategia de solución.
Fig. 1 Fig. 2 Fig. 3
...
1
4
9

110. 4.° primaria
L U D O M A T I C
INGENIO
110
● Exponente cero
Ejemplos:
Ejemplos:
● Exponente uno
● Multiplicación de potencias de igual base
● División de potencias de igual base
A continuación, tenemos las siguientes propiedades:
■ 80
= 1
■ 100
= 1
■ 51
= 5
■ 451
= 45
■ 20141
= 2014
PROPIEDADES DE LA POTENCIACIÓN
Para multiplicar potencias de igual base,
ponemos la misma base y sumamos los
exponentes.
Para dividir potencias que poseen la misma
base, debemos restar los exponentes.
Ejemplos:
■ 22
× 23
= 22 + 3
= 25
■ 54
× 56
= 54 + 6
= 510
am
× an
= am+n
Ejemplos:
■ 79
■ 28
÷ 25
= 28 – 5
=23
= 8
75
= 79 – 5
= 74
am
an
am – n
=
a = 1
0
a = a
1
8 cm
4 cm
PROPIEDADES
DE LA POTENCIACIÓN
En el ancho de este piso,
hay 4 losetas y, en el largo,
8. El total de losetas que
hay en el piso es 4 × 8 = 32.
¡Qué curioso! Si escribimos la operación como
potencias de 2, obtendríamos lo siguiente:
¿Habrá alguna relación entre la multiplicación
de bases iguales y sus exponentes?
4 × 8 = 32
2 × 2 = 2
2 3 5
Las propiedades de la
potenciación son las que
permiten resolver, por
diferentes métodos, una
potencia.
¿Cuáles son las
propiedades
de la
potenciación?
Importante :
La base “a” debe ser
diferente de cero.
a ≠ 0
2
TALLER

111. L U D O M A T I C
INGENIO
Álgebra
111
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Califica como verdadero o falso
los siguientes casos. Argumenta tu
respuesta.
I. 50
+ 60
= 1 ( )
II. 50
+ 51
= 6 ( )
III. ( )
Resolución:
a) Desarrollamos cada caso:
I. 50
+ 60
= 1 + 1 = 2 ≠ 1 ( F)
II. 50
+ 51
= 1 + 5 = 6 = 6 (V)
III. (V)
b) Los valores de verdad son FVV.
2014
2014
= 2014
10
9
2014
2014
10
9
= 2014 = 2014 = 2014
10 – 9 1
Si en la operación:
Cada recuadro se completa con el
número 2 y se opera, ¿qué resultado
se obtiene?
Resolución:
a) Reemplazamos en el recuadro.
b) Efectuamos la operación:
c) Se obtiene 35.
+ + ×
0 1 2 3
+ + ×
0 1 2
2 2 2 2
3
= 2 + 2 + 2
= 2 + 2 + 2
= 1 + 2 + 32
= 35
0
0
1
1 5
2 + 3
En un piso rectangular, se tiene que
en el ancho hay 3 losetas cuadradas
y, en el largo, 9 losetas. Si el total de
losetas que hay en el piso es 3a
.
Determina el valor de a.
Resolución:
a) Graficamos el problema:
b) El número de losetas del piso es
3 × 9 = 31
× 32
= 31 + 2
= 33
c)
Según el dato, la cantidad de
losetas es 3a
; entonces, igualamos
3a
= 33
. Se deduce que el valor de a
es 3.
La cantidad de cubos que se muestra
en la figura está representada por
Completa los recuadros vacíos.
Resolución:
a) La cantidad de cubos que hay es
6 × 6 × 6 = 216 = 63
b) Entonces, los recuadros vacíos se
completan así:
61
× 6 = 6
× 6 = 6
1 2 3
6

112. 4.° primaria
L U D O M A T I C
INGENIO
112
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
Indicadores de evaluación
Aplico las propiedades de una potenciación.
Completo operaciones aplicando las propiedades
de la potenciación.
Resuelvo problemas con propiedades de la
potenciación.
Completa las siguientes operaciones y
comparte tus respuestas.
● 5 × 5 = 5
● 7 × 7 = 7
● 4 ×4 ×4 = 4
● 9 ×9 ×9 = 9
● 10 = 10
6 4
5 3
3
3 8 2
4 8
= 5
= 7
= 9
5
7
9
5
7
9
16
5
10
10
3
4 8
6
●
●
●
● 5 × 5 = 5
María tiene varias piezas cuadradas
de 2 cm de lado y desea formar un
rectángulo de 4 cm de ancho y 8 cm
de largo. ¿Cuántas piezas necesita?
Elabora una estrategia de solución.
Si en la operación:
Cada recuadro se completa con el
número 3; luego, en la operación:
Cada recuadro se completa con el
número 2 y se opera. ¿Cuál de los si-
guientes enunciados es verdadero?
I. A B
II. A B
III. A = B
Elabora tu estrategia de solución.
+ ×
5 3 0 1
A=
×
6 4 7
B= ÷
3
1
6
7
3
5
6 × 6
7 × 7
6
7
3
2
2
0 0
4
4
6
●
●
● (1+2) + 1 + 2
Relaciona la operación con su
resultado.
1
6
7
3
5

113. L U D O M A T I C
INGENIO
Álgebra
113
● √4 Se lee: “Raíz cuadrada de cuatro”.
● √8 Se lee: “Raíz cúbica de ocho”.
● √125 Se lee: “Raíz cúbica de ciento veinticinco”.
TÉRMINOS DE LA RADICACIÓN
Ejemplos:
LECTURA Y ESCRITURA DE UNA RAÍZ
√125 = 5 5 =125
Radicando
Índice
Raíz
3
3
3
3
● √8 = 2 2 = 8 ● √64 = 8 8 =64
2
3
3
NOCIÓN DE RADICACIÓN
■
De nuestro ejemplo, tenemos que
64 cubitos forman un cubo de 4 cubitos
por lado; es decir, 4 × 4 × 4 = 64
3 veces
De esta expresión, obtenemos lo siguiente:
√64 = 4 43
= 64
Radicación
3
}
}
Para construir este
bloque, he utilizado
64 cubitos y en cada
lado he colocado 4.
¿Habrá alguna relación
entre el total de cubitos
utilizados y la cantidad
que va en cada lado?
RADICACIÓN
¿Qué es la
radicación?
Es una operación que consiste
en buscar un número llamado
raíz , tal que mutiplicado por sí
mismo una cantidad de veces
(índice), resulte otro número
denominado radicando.
n
Índice
Radicando
√b = a Raíz
Recuerda
Cuando el índice
es 2, no se escribe
y se lee raíz
cuadrada.
3
TALLER

114. 4.° primaria
L U D O M A T I C
INGENIO
114
ANALIZAMOS Y APRENDEMOS
1 2
4
3 Calcula el valor de la operación:
Resolución:
a) Reducimos la operación:
b) El valor de G es 5.
G = √5 + √16 + √√16
G = √5 + 4 + √4
G = √9 + √4
G = 3 + 2
G = 5
}
}
4 4
G = √5 + √16 + √√16
Se ha construido una base cuadrada
con 64 losetas cuadradas de igual
tamaño. ¿Cuántas losetas deben ir
en cada lado de la base? Elabora tu
estrategia de solución.
Resolución:
a) Supongamos que la base cuadrada
tiene 4 losetas.
La cantidad de losetas de cada lado
se obtiene así:
√4 = 2
b) En el caso de tener 64 losetas, la
cantidad que va en cada lado es
√64 = 8
c) Por lo tanto, hay 8 losetas en cada lado.
2
2
Si:
Determina y argumenta el valor de
verdad de las proposiciones:
I. 2 es la raíz.
II. 3 es el radicando.
III. 8 es el índice.
Resolución:
a) Identificamos los elementos de la
radicación.
b) Analizamos cada caso:
I. Es verdadero, porque 2 es la raíz.
II. Es falso, porque 3 es el índice.
III.Esfalso,porque8 eselradicando.
c)Elvalordeverdaddelasproposiciones
es VFF.
√8 = 2 23
= 8
3
√8 = 2 23
= 8
Índice
Radicando Raíz
3
Completa los recuadros en blanco.
Resolución:
a) Completamos las operaciones:
2
3
3
5
5
● √64 = 4 4 = 64
● √ 100 = 10 10 = 100
● √32 = 2 2 = 32
● √64 =
●√ = 10
● √32 = 2
3
4
100

115. L U D O M A T I C
INGENIO
Álgebra
115
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Identifico los elementos de la radicación.
Calculo el valor de una operación con
radicación.
Completo los elementos que faltan en una
radicación.
Resuelvo problemas con radicación.
Califica y argumenta como
verdadero o falso las siguientes
proposiciones:
I. La raíz de es 9.
II. El radicando en es 2.
III. En el índice es 8.
IV. En , el índice es 2.
√81
√25 = 5
√8
3
√36 = 6
Completa los recuadros en blanco
de las operaciones y comunica tus
resultados.
● √125 = =
● =8 =
● √32 =2 =
3 3
Si:
Determina el valor de las siguientes
operaciones:
■ A + B ■ B + C ■ A + B + C + D
A = √36 + √64 – √25
B = √√81 + √9 + √4
C = √√4 + √25 + √4
D = √16 + √25
Se ha construido un cubo con 125
cubitos de igual tamaño. ¿Cuántos
cubitos van en cada lado del cubo?
Elabora una estrategia de solución.

116. PROYECTO DE APRENDIZAJE N.0
1
PRESUPUESTO PARA ENLOSAR EL AULA
5. Evaluación
1. Situación problemática
El aula del 4.º grado necesita ser ambientada porque
los estudiantes necesitan un ambiente agradable
en el cual puedan desempeñar sus labores. Enlosar
el piso del aula es un primer paso para lograr este objetivo.
2. Finalidad
– Elaborar un presupuesto para enlosar el piso del aula.
– Comprender la utilidad de la potenciación en situaciones de
contexto real como el cálculo del área de una loseta cuadrada
y el área del piso a enlosar.
– Determinar la cantidad de losetas necesarias para enlosar el piso.
3. Recursos materiales
Presupuesto de costos de losetas. Wincha, papelotes, plumones.
Presupuesto de mano de obra. Cinta adhesiva, goma.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1.ª etapa 2.ª etapa
Organícense en equipos de 4
integrantes.
Coloquensobrelamesalospresupuestos
que han traido sobre el costo de las
losetas y el de mano de obra.
Analicen ambos presupuestos y
determinen cuáles son las más
convenientes para realizar el
proyecto.
Con la ayuda de la wincha, miden el piso
del salón y determinan su área. Del mismo
modo, se calcula el área de la loseta.
Determinan la cantidad de losetas a
necesitaryelcostoqueestolesdemanda.
Elaboran su presupuesto en un papelote y
lo exponen en la clase. Deben considerar el
costo de las losetas y el de mano de obra.
INGENIO
116

117. Observa la imagen y contesta
UNIDAD
2
Aprendemos a:
Cultivamos valores
Estar prevenidos
•
Educación para la
gestión de riesgos.
• Responsabilidad.
¿Qué observas en la figura?
¿Sabes lo que es estar prevenidos frente a un sismo?
¿En tu colegio hay zonas de seguridad en caso de sismo?
• Identificar los elementos de una expresión
algebraica.
• Clasificar las expresiones algebraicas de
acuerdo al número de términos.
• Expresar, mediante lenguaje algebraico,
enunciados en lenguaje usual.
• Resolver problemas de diferentes contextos
que impliquen el uso de las expresiones
algebraicas.

118. INGENIO
4.° primaria
L U D O M A T I C
118
1 2
4 5
Y
X
3
6
7 8 9
Z
Jugamos y aprendemos
Nos organizamos
FORMAMOS EXPRESIONES
CON NÚMEROS Y L E TRAS
LABORATORIO
2
1. Formen equipos de 4 integrantes.
2. Cada integrante debe traer una cartulina, una
tijera y un plumón.
3. Los integrantes de cada equipo deben recortar
tarjetas cuadradas del mismo tamaño.
4. En algunas tarjetas recortadas, escriban las letras
X; Y; Z (una letra por tarjeta) y en otras los números
del 1 al 9 (un número por tarjeta). (Ver fig.1).
5. Pueden repetir las letras y los números en
diferentes tarjetas.
6. Utilizando 3 tarjetas formarán expresiones del
tipo:
1. Las tarjetas recortadas y escritas las colocan sobre
la mesa de trabajo y los equipos se disponen a
comenzar.
2. Cada equipo debe resolver los siguientes
problemas, empleando sus tarjetas.
Problema 1. ¿Cuántas expresiones diferentes
del tipo mostrado pueden formar con los
números 2; 3; 4 y las letras X e Y?
Problema 2. ¿Cuántas expresiones diferentes
del tipo mostrado pueden formar con los
números pares que tenemos y la letra Z?
3. Gana el equipo que encuentra más expresiones
correctas de las preguntas en el menor tiempo
posible.
número
número
letra
(Fig.1)

119. INGENIO
L U D O M A T I C
Álgebra
119
Veamos:
Ejemplos:
L
L
Son términos algebraicos:
Números
Letra
16 L2
ELEMENTOS DE UN TÉRMINO ALGEBRAICO
Coeficiente
Parte literal
Exponentes
4 x3
y5
}
Son 3:
1. Coeficiente
2. Parte literal (letras o variables)
3. Exponentes
NOCIÓN DE TÉRMINO ALGEBRAICO
■ 5 x ■ 15 x 3
y4
■ 8 x y ■ 8 x yz
■ 18 a2
b ■ 13a2
b3
c5
■ De nuestro ejemplo:
Como el área de una loseta cuadrada es L2
, el área
que se forma con 16 de esas losetas es...
L2
= 16 L2
¿Qué es un término
algebraico?
Es una expresión algebraica
que une números y letras. No
incluye las operaciones de
adición y sustracción.
TÉRMINO ALGEBRAICO
TALLER
4
Esta área representa un término algebraico, porque está formado por una parte numérica
y otra literal.
El área de una loseta
cuadrada
es L × L = L2
. Entonces, el
área del piso mostrado es
9L2
.
¿Cuál será el área de un
piso formado con 16 de
esas losetas?

120. INGENIO
4.° primaria
L U D O M A T I C
120
ANALIZAMOS Y APRENDEMOS
1 2
3 4
En el término algebraico:
5 x3
¿Cuántas de las siguientes
proposiciones son verdaderas?
I. Su coeficiente es 5. ( )
II. Su parte literal es 5 y x. ( )
III. El exponente de su variable es 3. ( )
Resolución:
a) Identificamos los elementos del
término algebraico.
b) Analizamos las proposiciones.
I. Es verdadero: su coeficiente es 5.
II. Es falso: la parte literal solo es x.
III. Es verdadero: su exponente es 3.
c) Por lo tanto, hay 2 proposiciones
verdaderas.
Exponente
Parte literal
Coeficiente
5 x3
En el término algebraico:
(a + 1)xa
y2a
Si su coeficiente es 4, determina
la suma de los exponentes de sus
variables. Elabora una estrategia de
solución.
Resolución:
a)Deldato,sabemosqueelcoeficiente
es 4; entonces:
a + 1 = 4
a = 4 – 1
a = 3
b)Ahora,conrespectoalosexponentes
tenemos.
■ Exponente de x:
a = 3
■ Exponente de y:
2a = 2(3) = 6
■ La suma es 3 + 6 = 9.
c) Por lo tanto, la suma de los
exponentes es 9.
Si un lápiz cuesta S/. x, encuentra el
término algebraico que representa el
gasto de la compra de los lápices de
la figura.
Resolución:
a) En la figura, hay 7 lápices.
b) El gasto es igual a la cantidad de
lápices multiplicado por su precio;
entonces: 7 x
c) Por lo tanto, el término algebraico
es 7 x.
Se tiene el término algebraico:
Las tarjetas:
Si estas tarjetas las colocas en los
recuadros del término algebraico,
¿cuántos términos algebraicos
diferentes puedes formar? Elabora
una estrategia de solución.
Resolución:
a) Escribimos todos los términos posibles
que puedas formar.
b) Se puede formar 6 términos
algebraicos diferentes.
x
3 ; 4 y 5
3 3 4
4 5 3
x x x
; ;
4 5 5
5 3 4
x x x
; ;

121. INGENIO
L U D O M A T I C
Álgebra
121
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Identifico los elementos de un término algebraico.
Completo los elementos que faltan en una igualdad
de términos algebraicos.
Resuelvo problemas con términos algebraicos.
Si cada loro cuesta S/. x, representa
en forma algebraica el gasto de com-
prar los loros de la figura.
En un término algebraico de 2
variables, su coeficiente es 12 y el
exponente de “x” es el mayor número
impar de una cifra. El exponente de
“y” es el mayor número par de una
cifra. Escribe el término algebraico.
En la figura, se muestra el precio de
un litro de aceite. ¿Cuánto costarán
5 botellas como la mostrada?
S/. a
x
Se tiene el término algebraico:
Y las tarjetas:
Si estas tarjetas las colocas en los
recuadros del término algebraico,
¿cuántos términos algebraicos
diferentes puedes formar si
obligatoriamente el coeficiente
debe ser un número par? Elabora
una estrategia de solución.
2 ; 3 ; 4 y 5

122. INGENIO
4.° primaria
L U D O M A T I C
122
Veamos
● Monomio
Es la expresión algebraica formada por
un solo término.
De nuestro ejemplo, el costo de las
pelotas: 3a es un monomio.
Ejemplos:
● Polinomio
Es la expresión algebraica formada por
2 o más términos.
De nuestro ejemplo, la expresión: 4x+y
es un polinomio.
Ejemplos:
Principales polinomios
Entre los principales polinomios, tenemos lo
siguiente:
■ Binomio
Está formado por dos términos algebraicos.
Ejemplos:
■ Trinomio
Está formado por tres términos algebraicos.
Ejemplos:
■ 5 x4
■ 12 x5
y2
■ 5 x3
+ 2 x+ 1
■ 8 x3
+ 4 y2
+ x + y
■ 3 x4
+ 4y
■ 6x – 7y
■ 5 ab + b
■ 6 x4
+ 4 y – y3
■ 2 x – 7 y + xy
■ a3
b + b + a2
CLASIFICACIÓN DE EXPRESIONES ALGEBRAICAS
CLASES DE EXPRESIONES
ALGEBRAICAS
TALLER
5
El costo del comedor se
puede simbolizar como:
4x + y, donde “x” representa
el costo de una silla e “y”
el costo de una mesa.
El costo de las pelotas
que tengo se puede
representar como: 3a,
donde “a” representa el
costo de una pelota.
¿Qué clases
de expresiones
algebraicas
conocemos?
Las clases de expresiones
algebraicas son
● Monomio ● Polinomio

123. INGENIO
L U D O M A T I C
Álgebra
123
ANALIZAMOS Y APRENDEMOS
2
3 4
1
El costo de una cuchara es S/. x; el de
un tenedor es S/. y. Representa el costo
de cada figura y clasifícalas como
monomio o polinomio.
Resolución:
a) Del dato:
Cucharas: S/. x
Tenedores: S/. y
b) Entonces, se tiene lo siguiente:
x + y (Polinomio)
3y (Monomio)
6y + 6x
(Polinomio)
Telassimtiene“a”pelotasy“b”muñecas;
Milagros tiene 2 pelotas y 3 muñecas.
Si unen sus juguetes, determina una
expresión que represente la cantidad
de juguetes que poseen. Elabora una
estrategia de solución.
Resolución:
a) Del dato:
Cantidad de pelotas: a + 2
Cantidad de muñecas: b + 3
b) La cantidad de juguetes es
a + 2 + b + 3 = a + b + 5.
c) Por lo tanto, la expresión que
representa la cantidad de juguetes
es a + b + 5.
Representa en forma simbólica la
expresión: “el triple de un número
sumado con el doble de otro”.
Resolución:
a) Simbolizamos los números.
Sea un número x
El otro número es y
b) Simbolizamos el enunciado:
El triple de un número sumado con el
doble de otro.
c) La representación simbólica es:
3x + 2y
3 x +
2 y
Relacionalosobjetosconsupreciomediante
flechas: si el precio de una silla es S/. x, de
una mesa, S/. y; de una lámpara, S/. z.
x + y + z
4 x + y
3 x
x + y + z
4 x + y
3 x
Resolución:
a) De acuerdo con la definición, se tiene:

124. INGENIO
4.° primaria
L U D O M A T I C
124
PIENSO Y RESUELVO
AUTOEVALUACIÓN
2
3
Indicadores de evaluación
Clasifico las expresiones algebraicas.
Relaciono las expresiones algebraicas.
Represento en forma simbólica expresiones
algebraicas.
Resuelvo problemas con expresiones algebraicas.
Relaciona correctamente mediante
flechas:
xyz
xy + yz
x + y + z
x2
y2
z2
x + y
Monomio
Binomio
Trinomio
El precio de un perro es S/. x, el de una
culebra es S/. y; el de un caracol S/. z.
Representa en forma algebraica el
gasto al comprar 2 perros, 4 culebras
y 3 caracoles.
4 Nelly tiene “a” pelotas y “b” muñecas
y Teresa tiene 4 pelotas y 5 muñecas.
Si unen sus juguetes, determina una
expresión que represente la cantidad
de juguetes que poseen.
Elabora una estrategia de solución.
1 Clasifica las siguientes expresiones
algebraicas en monomios y polinomios.
I. (10 – 5 + 6) x
II. 7 x2
y + 5 x y – y
III. x + y + z
IV. 4x + 2x + 3x

125. EXPRESIONES ALGEBRAICAS EN LA VIDA DIARIA
PROYECTO DE APRENDIZAJE N.0
2
INGENIO
1. Situación problemática
A diario, vemos por la televisión propagandas sobre el precio
de determinados productos. Por ejemplo: en los mostradores de las tiendas
exhiben ofertas; en las conversaciones las personas hablan
de los precios, etc.
Muchas de estas expresiones utilizadas pueden
traducirse al lenguaje algebraico. El uso de expresiones
algebraicas para representar fórmulas nos permiten
resolver una variedad de problemas.
2. Finalidad
- Representar en forma algebraica situaciones de la vida cotidiana.
- Comprender la utilidad de las expresiones algebraicas en el empleo de fórmulas.
3. Recursos materiales
Revistas, periódicos.
Goma, tijera, papelote.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas. NO ESCRIBIR AQUÍ
1.ª etapa 2.ª etapa
 Organícense en equipos de 4
integrantes.
Planteen frases que se puedan
representar en forma simbólica con
ayuda de las expresiones algebraicas.
Busquen en revistas y periódicos las
palabras que van a utilizar en sus
frases.
En un papelote, recorten y peguen las
palabras que forman sus frases.
Cada frase debe ir acompañada
de su representación simbólica.
Exponen en la clase sus frases y
las pegan en las paredes del aula.
125

126. EXPRESIONES
ALGEBRAICAS II
Cultivamos valores
Educación para
la paz.
Tolerancia.
Aprendemos a:
• Determinar el valor numérico de una expresión
algebraica.
• Identificar y reducir términos semejantes.
• Resolver problemas de diferentes contextos que
impliquen el uso del valor numérico y los términos
semejantes.
Observa la imagen y contesta
¿Qué entiendes por vivir en paz?
¿Conoces cuál es el símbolo de la paz?
¿Cómo crees tú que podemos vivir en el mundo en paz y armonía?
Vivir en paz
UNIDAD
3

127. L U D O M A T I C
INGENIO
Álgebra
127
COMPLETAMOS
EL TABLERO
1. Organícense en parejas.
2. Cada pareja debe traer una cartulina, dos
dados (uno blanco y el otro negro) y varias
chapas de gaseosas.
3. En cartulina, elaborar un tablero con las medi-
das y el cuadro que se muestra. (Ver fig. 1).
3
LABORATORIO
Nos organizamos
1. Para iniciar el juego, cada jugador lanza un
dado: el que obtenga el mayor número inicia.
2. El jugador que inicia lanza los dos dados. Al
resultado del dado blanco lo multiplica por 2 y
le suma el resultado del dado negro.
3. El resultado final obtenido lo ubica en el tablero y
le coloca una chapa para indicar que es suyo.
4. El siguiente jugador realiza la misma operación y
continúan así, turnándose, uno después del otro.
5. Si un jugador obtiene un resultado que ya había
salido, retira la chapa del opositor y coloca la
suya.
6. Si sale el mismo número para el jugador que está
en turno, no se agregará o acumulará ninguna
chapa. Seguirá manteniendo la suya.
Jugamos y aprendemos
Gana el jugador que tiene
más chapas y que complete
todo el tablero.
4 5 6
7 8 9
10 11 12
13 14 15
16 17 18
12 cm
20 cm
(Fig.1)

128. 4.° primaria
L U D O M A T I C
INGENIO
128
VALOR NUMÉRICO DE UNA
EXPRESIÓN ALGEBRAICA
TALLER
6
Ejemplo:
Determina el valor numérico del monomio: A = 3 x y z, cuando x = 2 ; y = 3 ; z = 4
Resolución:
Reemplazamos los valores de las variables en el monomio.
VALOR NUMÉRICO DE UN POLINOMIO
Es el resultado que se obtiene al sustituir las variables o letras por valores numéricos al ser
operadas numericamente.
VALOR NUMÉRICO DE UN MONOMIO
S/. 3 S/. 4
El valor numérico de un
monomio es el número que se
obtiene al sustituir las letras por
los números.
A = 3 x y z
3(2)(3)(4)
6 (3)(4)
18 (4)
72
■
Por lo tanto, el gasto es de S/.
26 y se obtiene empleando el
valor númerico de un polinomio.
De nuestro ejemplo, el gasto de la compra es...
2x + 5y
arroz leche
De donde x = 3 ; y = 4 (Precios)
entonces el gasto es...
2x + 5y
2(3) + 5(4)
6 + 20
26
}
}
¿Cuánto se gasta
al comprar 2 kg de arroz
y 5 latas de leche?
■ 2kg de arroz cuesta
S/. 3 2×3 = S/. 6
■ 5 latas de leche cuesta
S/. 4 5×4 = S/. 20
En total se gastó
6 + 20 = S/. 26
¿Qué es el valor
numérico de un
monomio?

129. L U D O M A T I C
INGENIO
Álgebra
129
Calcula el gasto que demanda
comprar:
Si un crayón cuesta S/. 2 ; un libro,
S/. 10, y la manzana es de regalo.
Resolución:
a) En la compra de crayolas, se gasta
(cantidad) × (precio) = 3 × 2 = 6
Nuevos Soles.
b) En la compra de libros, se gasta
(cantidad) × (precio) = 3 × 10 = 30
Nuevos Soles.
c) El total del gasto es 6 + 30 = 36
Nuevos Soles.
ANALIZAMOS Y APRENDEMOS
Determina el valor numérico de
A= x2
+ 2x + 1, cuando x = 3 y
comunica tu respuesta.
Resolución:
a) Reemplazamos el valor de “x”
en la expresión algebraica.
A= (3)2
+ 2(3) + 1
b) Desarrollamos la operación
combinada.
c) El valor numérico de la expresión
algebraica es 16.
A= (3)2
+ 2 (3) + 1
9 + 6 + 1
15 + 1
16
1 2
Completa la tabla:
y comunica por respuesta la suma
del mayor y menor valor obtenido.
Resolución:
a) Completamos la tabla:
b) El mayor valor es 12 y el menor es 6.
c) Por lo tanto, la suma del mayor y
menor valor es...
12 + 6 = 18
x = 2; y = 3
x = 1; y = 4
3x + 2y xy + 2
x = 2; y = 3
x = 1; y = 4
3x + 2y xy + 2
12 8
11 6
3
El precio de costo de pares de zapato
está determinado por la expresión
algebraica: (20x – 5), donde “x”
representa el número de pares de
zapatos. ¿Cuánto cuestan 3 pares de
zapatos? Elabora tu estrategia de
solución.
Resolución:
a) Como “x” representa el número de
zapatos, basta con reemplazar x = 3
en la expresión algebraica:
(20x – 5).
b) Entonces:
= 20(3) – 5
= 60 – 5
= 55
c) Por lo tanto, 3 pares de zapato
cuestan S/. 55.
4

130. 4.° primaria
L U D O M A T I C
INGENIO
130
PIENSO Y RESUELVO
Determina el precio de cada peluche
si x = 3 ; y = 2.
s/.3x2
s/.6xy s/.2x3
y2
s/.3x2
y
1
AUTOEVALUACIÓN
En una juguetería, se tiene los siguien-
tes productos:
Si una persona compra 2
hipopótamos, 3 patos y una rana;
¿cuánto gastará?
S/. 5
S/. 3
S/. 2
3
Calcula el valor numérico de los
siguientes polinomios y comunica tus
respuestas.
a) 3x2
– 2× + 1, para x = 2
b) (x+1)(x+3), para x = 4
c) 5x – 2y, para x = 2 ; y = 3
d) x2
+ y2
+ xy, para x = 2 ; y = 3
e) x + x y + y, para x = 4 ; y = 5
2
Indicadores de evaluación
Determino el valor numérico de una expresión
algebraica.
Completo tablas aplicando el valor numérico de una
expresión algebraica.
Resuelvo problemas aplicando el valor numérico de una
expresión algebraica.
Del siguiente croquis:
Determina la distancia que recorre la
persona que va del punto A hasta B.
Elabora una estrategia de solución.
4
A
B
x
●
●
2×
5×

131. L U D O M A T I C
INGENIO
Álgebra
131
TÉRMINOS SEMEJANTES
Ejemplo:
Son términos semejantes: No son términos semejantes:
Porque el 8 no tiene la
parte literal “x”.
Porque los exponentes
de “x” no son iguales.
Porque los exponentes
de “x” e “y” no son
iguales.
■ 6a , 8a
■ 4x2
y3
; 3x2
y3
; 7x2
y3
■ 7x ; x ;10x
■ 7x ; 6x ; 8
■ 3xy ; 9x2
y
■ 6x2
y ; 10xy2
; 7xy
NOCIÓN DE TÉRMINOS SEMEJANTES
De nuestro ejemplo, en las tarjetas de Silver y Manchas tenemos lo siguiente:
Son términos semejantes; por lo tanto, pertenecen a la misma caballería.
3x2
y4
; 6x2
y4
exponentes iguales
igual parte literal
Silver Manchas
Silver Potrillo Manchas
3x2
y4
3x3
y3 6x2
y4
TALLER
7
Si las tarjetas que portan los caballos indican
la caballería a la que pertenecen, ¿qué
caballos pertenecen a la misma caballería? Pertenecen
a la misma
caballería,
los animales
en cuyas
tarjetas sus
términos son
semejantes.
¿Qué son los términos
semejantes?
Dos o más términos son semejantes si
tienen la misma parte literal; es decir,
las mismas letras afectadas con los
mismos exponentes.

132. 4.° primaria
L U D O M A T I C
INGENIO
132
ANALIZAMOS Y APRENDEMOS
Comunica si los siguientes términos
son semejantes, colocando
verdadero (V) o falso(F) :
I. 12a2
b ; 7ab2
( )
II. 8xy ; 7xy ( )
III. 5a ; 8a ( )
IV. 5x2
y4
; 5x4
y2
( )
Resolución:
a) Calificamos cada caso:
I. 12a2
b ; 7ab2
( F )
II. 8xy ; 7xy ( V )
III. 5a ; 8a ( V )
IV. 5x2
y4
; 5x4
y2
( F )
b) Los valores de verdad son FVVF.
1
Si los términos mostrados son
semejantes:
Determina la suma de los números que
van en los recuadros en blanco.
Resolución:
a) Por ser semejantes, tienen los mismos
exponentes en sus variables.
Entonces:
b) Los números que van en los
recuadros son 5 ; 2 y 4.
c) Por lo tanto, la suma de esos
números es 5 + 2 + 4 = 11.
7x2
y z4
; 3x y5
z
7x2
y z4
; 3x y5
z
5 2 4
2
Si los términos:
Son semejantes, determina el valor de
P = a + b. Argumenta tu respuesta.
Resolución:
a)
Por ser semejantes, los exponentes
en sus variables son iguales;
entonces:
■ Del exponente de x:
a + 1 = 4
a = 3
■ Del exponente de y:
2b = 8
b = 4
b) Se pide determinar lo siguiente:
P = a + b
P = 3 + 4
P = 7
12xa+1
y8
; 6x4
y2b
3 Si las expresiones en las tarjetas
representan términos semejantes y sus
coeficientes, los precios de los peluches,
determina cuánto cuesta cada
peluche.
Elabora una estrategia de solución.
Resolución:
a)
Elaboro mi estrategia.
Por ser semejantes, los exponentes en
sus variables son iguales.
b) Ejecuto mi estrategia.
■ Del exponente de x:
a = 3
■ Del exponente de y:
b = 5
c) De los coeficientes:
■ ab = (3)(5) = 15
■ a + b = 3 + 5 = 8
d) Por lo tanto, como los coeficientes
representan los precios de los peluches,
uno cuesta 8 soles y el otro 15 soles.
S/. abxa
yb S/. (a + b)x3
y5
4

133. L U D O M A T I C
INGENIO
Álgebra
133
PIENSO Y RESUELVO
Comunica si las siguientes
proposiciones son verdaderas o falsas.
■ 3 a2
b es semejante con 5a2
b. ( )
■ 6 ab y 5a2
b no son semejantes. ( )
■ ax
b y a3
b son semejantes si x = 3. ( )
1
Completa los números y letras en los
recuadros en blanco.
Argumenta tu respuesta.
a = 5 b
4
3
2
Los términos en las tarjetas de los
carros son semejantes; además el
valor de a indica la cantidad de
autos que hay de ese modelo y el
valor de b, la cantidad de autos
del otro modelo. ¿Cuántos autos
hay en total para ambos modelos?
Elabora tu estrategia de solución.
x7
y5b
xa+2
y10
3 Rocío observa que los términos:
P = xa+1
yb+2
; Q = (3a+b)x4
y8
Son semejantes y se da cuenta de que
es posible determinar el coeficiente
de Q. ¿Cuál es ese coeficiente?
Elabora tu estrategia de solución.
4
AUTOEVALUACIÓN
Indicadores de evaluación
Identifico términos semejantes.
Completo los exponentes de términos semejantes.
Determino el valor numérico de expresiones,
aplicando términos semejantes.
Resuelvo problemas que involucran el uso de los
términos semejantes.

134. 4.° primaria
L U D O M A T I C
INGENIO
134
TALLER
REDUCCIÓN DE TÉRMINOS
SEMEJANTES
8
¿Cómo se reduce términos
semejantes?
Para reducir términos semejante basta
con sumar o restar sus coeficientes y
colocar la misma parte literal.
Ejemplo:
Determina la siguiente expresión:
Q = 15a – 5a – 3a
Resolución:
Q = 15a – 5a – 3a
Q = 10a – 3a
Q = 7a
FORMAS DE REDUCCIÓN
Caso 1:
Si tienes S/. 4 en un bolsillo y S/.2 en otro,
inmediatamente dirás “tengo S/.6”.
La operación que haz realizado es
S/. 4 + S/. 2 = S/.6.
Esta suma es posible porque tienen la
misma “parte literal” (S/.).
Caso 2:
Si tienes 4 manzanas y 3 peras, quieres
sumar lo siguiente:
“4 manzanas + 3 peras”
No se puede porque sus “partes literales”
(manzana y peras) no son iguales.
De nuestro ejemplo, el peso de los 3
caballos es...
6a + 5a + 8a
11a + 8a
19a
Por lo tanto, pesan 19a kg.
5a kg
6a kg 8a kg
Los caballos muestran el peso de
cada uno de ellos en función de
una expresión algebraica.
¿Cuánto pesan
los 3 caballos?
Cuando no se escribe el coeficiente de la parte literal,
se sobreentiende que es la unidad.

135. L U D O M A T I C
INGENIO
Álgebra
135
ANALIZAMOS Y APRENDEMOS
Reduce la siguiente operación:
H = 8x + 6x – 2x – 7x
Comunica tu respuesta.
Resolución:
a)Reducimos de izquierda a derecha
las operaciones.
H = 8x + 6x – 2x – 7x
H = 14x – 2x – 7x
H = 12x – 7x
H = 5x
b)El valor de la operación es 5x.
1 Completa las cantidades que deben
ir en los recuadros de la operación.
Resolución:
a) Completamos las cantidades:
10x + – 4x
16x –
10 x + – 4x
16x –
6x
4x
12x
2
Reduce la operación y determina el
valor de “a”, si:
axy = 8xy – 2xy + 6xy – 5xy
Resolución:
a) Reducimos la operación del
segundo miembro y luego lo
comparamos con el primero.
axy = 8xy – 2xy + 6xy – 5xy
6xy + 6xy – 5xy
12xy – 5xy
7xy
Al comparar se tiene:
a = 7
b) Por lo tanto, el valor de “a” es 7.
3 Sonia tiene a muñecas en su
armario, 2a en dormitorio y 3a en
su sala. ¿Cuántas muñecas tiene en
total?
Elabora una estrategia de solución.
Resolución:
a)Planteamos la estrategia.
Debemos sumar las cantidades de
muñecas para obtener el total.
b)Ejecutamos el plan.
a + 2a + 3a
3a + 3a
6a
c)Comunicamos la respuesta.
Las muñecas que tiene en total son
6a.
4

136. 4.° primaria
L U D O M A T I C
INGENIO
136
PIENSO Y RESUELVO
Reduce las siguientes operaciones:
G = 12x + 11x – 8x – 6x – 4x
M = 5x – 4x + 3x
N = 8a – 5a + 4a – 3a
P = 6xy + 4xy - 3xy - 2xy
Q = 18ab – 7ab – 6ab + 5ab
R = 12x + 8x + x + 4x – x – 2x
A = 6x – 4x + 5x – 3x+ x
Comparte tus resultados con tus
compañeros.
1 Completa las cantidades que deben
ir en los recuadros de la operación.
12 x + – 5x – 2x
20 x – – 2x
–
2
El resultado de la operación:
3x2
y5
– 2x2
y5
+ 8x2
y5
Es axb
yc
. Determina el valor de la
siguiente expresión: T = a+b+c
3 En las cajas, se indica la cantidad
de pelotas que tienen en su interior.
¿Cuántas pelotas hay en total en las
2 cajas?
3a 4a
4
Indicadores de evaluación
Reduzco operaciones con términos semejantes.
Completo términos en el desarrollo de una operación
con términos semejantes.
Calculo el valor de un coeficiente en el desarrollo de una
operación con términos semejantes.
Resuelvo problemas de contexto real o matemático que
involucraban la reducción de términos
semejantes.
AUTOEVALUACIÓN

137. CALCULAMOS VALORES NUMÉRICOS
EN EL AULA
PROYECTO DE APRENDIZAJE N.0
3
INGENIO
1.ª etapa 2.ª etapa
Organícense en equipos de 4
integrantes.
Escriban las fórmulas del área del
triángulo, rectángulo y cuadrado
en forma de expresiones
algebraicas.
Cada equipo elige una zona u
objeto del aula, el cual medirá,
y, usando el valor numérico,
determinará su área.
Con el centímetro o wincha, miden la
zona u objeto elegido para su proyecto.
 Determinan la forma geométrica
del objeto medido y reemplazan sus
valores numéricos, en la fórmula que le
corresponde, para calcular su área.
Calculadoelárea,elaboranunpapelote
en donde muestren las resultados
obtenidos y exponen en clase.
5. Evaluación
a
a
Área del
cuadrado
A= a2
h
b
Área del rectángulo
A= b x h
1. Situación problemática
El aula es el lugar de aprendizaje de los estudiantes y en ella podemos
encontrar diferentes situaciones de aprendizaje. El valor numérico nos
permite calcular el área de las diferentes zonas de nuestra aula como
el de la pizarra, las ventanas, etc.
2. Finalidad
- Calcular el área de las diferentes zonas, partes y/o elementos
del aula empleando el valor numérico.
- Concientizar a los estudiantes sobre la importancia del valor
numérico y su utilidad en el mundo que nos rodea.
3. Recursos materiales
Wincha, fórmulas del área del rectángulo, triángulo y cuadrado.
Papelote, plumones, cinta adhesiva.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
137

138. Aprender a convivir
Cultivamos valores
● Educación para la
convivencia, la paz
y la ciudadanía.
● Tolerancia.
GRADO DE UN
POLINOMIO
Aprendemos a:
●
Identificar el grado relativo y absoluto de un
monomio y un polinomio.
● Determinar el grado relativo y absoluto de un
monomio y un polinomio.
● Resolver situaciones problemáticas aplicando
el grado de un monomio y un polinomio.
Describe lo que observas en la figura
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es muy importante en tu familia?
UNIDAD
4

139. INGENIO
L U D O M A T I C
Álgebra
139
J UGAMOS
CON D ADOS
1. Organícense en parejas.
2. Cada pareja debe traer 4 dados.
3. Elaboren dos fichas como las mostradas,
(Ver fig 1 y 2) cada jugador toma una ficha.
Nos organizamos
1.
Para iniciar el juego, cada jugador toma dos
dados y los lanza.
2. Coloca los dados en la posición que han
caído, sobre los círculos de sus tarjetas y suma
sus resultados.
3. El que tenga la mayor suma gana el juego.
4. En caso de empatar en la suma, no hay
ganador en ese juego.
Jugamos y aprendemos
Gana el jugador que,
después de 10 juegos, tie-
ne más victorias.
4
LABORATORIO
+
+
Jugador 1
Jugador 2
(Fig. 1)
(Fig. 2)

140. INGENIO
4.° primaria
L U D O M A T I C
140
GRADO DE UN MONOMIO
■ Grado relativo de un monomio
El grado relativo es el exponente respecto a una letra o variable.
Veamos:
■ Grado absoluto de un monomio
El grado absoluto de un monomio es igual a la suma de los exponentes de su parte literal.
Veamos:
9x5
y2
G.A = 5+2 = 7 (Se lee grado absoluto del monomio es igual a 7)
NOCIÓN DE GRADO DE UN MONOMIO
G.R(x) = 5 (Se lee grado relativo a “x” es igual a 5).
G.R(y) = 2 (Se lee grado relativo a “y” es igual a 2).
9 x5
y2
■ En nuestro ejemplo, se cumple lo siguiente:
10 + b = 24 b = 14
Exponentes Coeficiente
Por lo tanto, se vende 14 borradores. Observa
que 14 es el exponente de “y”; entonces, es su grado.
}
}
TALLER
9
La expresión:
es un código secreto para saber la
cantidad de lapiceros y borradores
vendidos.
El coeficiente indica la cantidad de
lapiceros y borradores vendidos.
El exponente de “x” indica la
cantidad de lapiceros vendidos; la de
“y”, los borradores.
(a + b) xa
yb
En la expresión:
24 x10
yb
¿Cuántos
borradores se
ha vendido?
¿Qué es el grado
de un
monomio?
Es una característica que tiene
que ver con los exponentes de las
variables. Pueden ser de dos
tipos: relativo y absoluto.

141. INGENIO
L U D O M A T I C
Álgebra
141
ANALIZAMOS Y APRENDEMOS
Determina los grados relativos de “x”
en los siguientes monomios y representa
el orden de mayor a menor.
8x4
y5
; 5x6
y7
z8
; 3x3
y4
z5
Resolución:
a) Calculamos los G.R(x) en cada
monomio, entonces:
8x4
y5
G.R(x) = 4
5x6
y7
z8
G.R(x) = 6
3x3
y4
z5
G.R(x) = 3
b) Ordenamos de mayor a menor:
6 ; 4 ; 3
¿Cuál de los siguientes monomios
tiene mayor grado absoluto?
Resolución:
a) Calculamos los grados absolutos:
G.A = 7 + 2 + 1 = 10
G.A = 4 + 2 + 5 = 11
G.A = 4 + 4 + 2 = 10
b) El mayor grado absoluto es 11, por
lo tanto el monomio es
x7
y2
z ; 7 x4
y2
z5
; √25 x4
y4
z2
3
4
x7
y2
z
3
4
7x4
y2
z5
√25 x4
y4
z2
7x4
y2
z5
.
1 2
Utiliza los siguientes datos:
G.R(x) = 4
G.R(y) = 6
G.A = 15
y completa el monomio:
Resolución:
a) Completamos según los datos:
Como G.A = 15, entonces:
4 + 6 + = 15
10 + = 15
= 15 – 10
= 5
b) Luego:
8 x y z
8 x y z
8 x y z
4
4
6
6 5
3 Telassim dice que el grado relativo de
“x” del monomio xa+1
ya + 2
es 5. ¿Cuál
será su grado absoluto? Elabora una
estrategia de solución.
Resolución:
a)Elaboramos una estrategia.
Del G.R(x) determinamos el valor de
“a” y luego su G.A.
b)Ejecutamos el plan.
■ Del grado relativo de x, se tiene
lo siguiente:
G.R(x) = 5
a + 1 = 5
a = 4
■ Del grado relativo de y:
G.R(y) = a + 2 = 4 + 2 = 6
El monomio resulta ser P(x ; y) = x5
y6
.
c)Comunicamos la respuesta.
El grado absoluto es lo siguiente:
G.A = 5 + 6 = 11
4

142. INGENIO
4.° primaria
L U D O M A T I C
142
PIENSO Y RESUELVO
Completa la siguiente tabla,
determinando el grado relativo de sus
variables y el grado absoluto.
Monomio G.R (x) G.R (y) G.R (z) G.A
9x7
y3
z8
5x8
y4
z
12x6
y
9x6
y5
z3
7x3
y9
1 ¿Quién de los niños tiene la tarjeta
con el monomio de mayor grado
absoluto?
Argumenta tu respuesta.
Lucho María Pancho
x5
y7
z
6
7
9x4
y6
z5
√36 x4
y4
z6
2
Del monomio:
Completa sus exponentes si:
G.R(x) = 3
G.R(y) = 2G.R(x)
G.A = 13
4x y z
3 Pedro dice lo siguiente:
El grado relativo de x en
x2a
y(a+1)
es 8
¿Cuál será su grado absoluto?
Elabora una estrategia
de solución.
4
AUTOEVALUACIÓN
Indicadores de evaluación
Determino el grado relativo y absoluto de un
monomio.
Completo los exponentes de un monomio,
aplicando el grado relativo y absoluto.
Resuelvo problemas aplicando el grado de un
monomio.

143. INGENIO
L U D O M A T I C
Álgebra
143
GRADO DE UN POLINOMIO
■ Grado relativo de un polinomio
Es el mayor exponente que afecta a una variable. Veamos la expresión:
■ Grado absoluto de un polinomio
Es el mayor grado absoluto de sus términos. Veamos lo siguiente:
x3
y4
x2
y7 x6
y4
GR(x) = 6 (Grado relativo de “x” es igual a 6)
GR(y) = 7 (Grado relativo de “y” es igual a 7)
x6
y4
+ 6x2
y7
G.A = 10 (grado absoluto)
Es el mayor
5x3
y4
+ 7x5
y4
– 6x6
y4
}
}
}
10
7 9
En el juego “tiro al blanco”, el puntaje se
obtiene sumando los exponentes de las
variables que están en la cabeza de los
patitos.
Si se tiene 3 pelotas, ¿a cuál de los patitos
debemos apuntar para obtener el mayor
puntaje posible?.
GRADO DE UN POLINOMIO
TALLER
10
¿Qué es el grado
de un polinomio?
Es una característica de los
exponentes de sus variables.
Pueden ser de dos clases:
relativo y absoluto.

144. INGENIO
4.° primaria
L U D O M A T I C
144
ANALIZAMOS Y APRENDEMOS
Determina los grados relativos de “x”
e “y” en los siguientes polinomios.
Comunica tu respuesta.
P: 7x4
y5
+ 5x6
y7
Q: 3x3
y4
– 4x6
y3
Resolución:
a) Calculamos los grados relativos de
los polinomios.
7x4
y5
+ 5x6
y7
G.R(x) = 6
G.R(y) = 7
3x3
y4
- 4x6
y3
G.R(x) = 6
G.R(y) = 4
b) Comunicamos la respuesta.
Se tiene en P: G.R(x) = 6
G.R(y) = 7
Se tiene en Q: G.R(x) = 6
G.R(y) = 4
1 ¿Cuál de los siguientes polinomios
tiene mayor grado absoluto?
Resolución:
a) Determinamos los grados absolutos:
b) Comunicamos la respuesta.
Como 12 11, entonces el segundo
polinomio tiene mayor grado
absoluto.
■ 6x4
y5
– 8x5
y3
+ 7 x2
y9
■ 7x6
y5
+ 3x6
y6
+ 9x3
y8
■ 6x4
y5
– 8x5
y3
+ 7x2
y9
GA= 11
■ 7x6
y5
+ 3x6
y6
+ 9x3
y8
GA= 12
}
}
}
}
}
}
9 8 11
11 11
12
2
Del polinomio:
Completa sus exponentes, si:
G.R(x) = 6 ; G.R(y) = 7
y comunica su grado absoluto.
Resolución:
a) Completamos según los datos:
De donde:
G.A = 11
b) Comunicamos la respuesta.
Su G.A es 11
8x y3
+ 3x4
y
8x y3
+ 3x4
y
6 7
}
}
9 11
3
El grado relativo de “x” en el
polinomio:
xa+1
ya+1
+ x3
y2a
es 5
¿Cuál será el grado relativo
de “y”?
Telassim dice el siguiente problema:
Resolución:
a) Del dato:
GR(x) = 5
a + 1 = 5
a = 4
b) Comunicamos la respuesta.
El grado relativo de “y” es
G.R(y) = 2a = 2(4) = 8.
4

145. INGENIO
L U D O M A T I C
Álgebra
145
PIENSO Y RESUELVO
Completa la siguiente tabla,
determinando el grado relativo de
sus variables y el grado absoluto.
2
Del polinomio:
Completa sus exponentes, si:
G.R(x) = 5 ; G.R(y) = 4
e indica su grado absoluto.
3x y2
+ 5x3
y
3 Pedro dice que el grado relativo de
“x” en el polinomio 8xa
+ 6x4
es 5.
Menciona cuál será el grado absoluto
del polinomio.
9xa+2
– 3x2a
Elabora tu estrategia de solución.
4
AUTOEVALUACIÓN
Indicadores de evaluación
Determino el grado relativo y absoluto de un poli-
nomio.
Completo los exponentes de un polinomio,
aplicando el grado relativo y absoluto.
Resuelvo problemas aplicando el grado de un po-
linomio.
En la expresión:
(a+b) xa
yb
+ 4x3
y5
El grado relativo a “x” es 5, su grado
absoluto es 10.
Determina el valor de la siguiente
expresión: 2a +b
1
7x5
y3
– x6
z8
5x5
y4
+ 8x3
y9
8x4
y – 9y5
z3
2x6
y7
+ x5
y2
+ x5
z3
8x6
y5
– 5x4
y8
Polinomio G.R (x) G.R (y) G.r (z) G.A.

146. PROYECTO DE APRENDIZAJE N.0
4
POLINOMIOS EN LAS TIENDAS COMERCIALES
INGENIO
5. Evaluación
1.
Situación problemática
Los estudiantes necesitan aplicar los nuevos conocimientos que van adquiriendo.
Las tiendas comerciales son lugares ideales en donde pueden aplicarse dichos
conocimientos.
Al usar los polinomios podemos elaborar expresiones que nos permitan calcular
el costo de una cantidad determinada de productos de manera rápida y sencilla.
2. Finalidad
- Establecer polinomios que nos permitan determinar
el costo de una cantidad de productos específicos.
3. Recursos materiales
Periódicos, catálogos de precios de tiendas comerciales
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
1.ª etapa 2.ª etapa
Organícense en equipos de 4
integrantes.
En su periódico o en su catálogo
de precios, elijan un producto con
el que van a trabajar el proyecto.
Asegúrense que se encuentre
el precio unitario del producto
elegido.
Recuerde que: Costo = precio unitario
× cantidad. Establezca el polinomio del
costo del producto elegido en función
de la cantidad que se compra.
En un papelote, presenten el polinomio
del costo del producto elegido y calculen
el costo que le demanda la compra de 3;
5 y 6 cantidades de su producto. Pegan
recortes de sus productos en el papelote..
146

147. UNIDAD
5
Educación en derechos humanos
OPERACIONES CON
EXPRESIONES
ALGEBRAICAS I
Cultivamos valores
•
Educación para los
derecho humanos.
• Respeto.
Aprendemos a
•
Reducir operaciones de adición y sustracción con
expresiones algebraicas.
•
Plantear y resolver operaciones combinadas de
adición y sustracción con expresiones algebraicas.
•
Resolver situaciones problemáticas que requieran
la aplicación de las operaciones de adición y
sustracción con expresiones algebraicas.
Observa la imagen y contesta
¿Sabes qué es la Declaración Universal de los Derechos Humano?
¿Cuáles son tus derechos?
¿Cuándo se aprobó la Declaración Universal de Derechos Humanos?
ÁREA VERDE

148. 4.° primaria
L U D O M A T I C
INGENIO
148
5
LABORATORIO
1. Formen parejas.
2.
Elaboren tarjetas de cartulina como en la
figura 1.
3.
Traer un dado.
1. Ambos jugadores lanzan el dado. Quien
obtenga el mayor número, inicia el juego.
2. Colocan tarjetas boca abajo.
3. El jugador que inicia el juego voltea dos
tarjetas. Si estas tienen las mismas figuras,
las recoge y continúa jugando. En caso
contrario, le cede el turno al otro jugador.
4. Se continúa jugando hasta que todas las
tarjetas queden volteadas.
5. Cada jugador cuenta la cantidad de tarjetas
que tiene.
V O LT E AM O S
T A RJ E T A S
Nos organizamos
Jugamos y aprendemos
Gana el juego el
jugador que tiene
más tarjetas.
Fig.1

149. L U D O M A T I C
INGENIO
Álgebra
149
TALLER
ADICIÓN Y SUSTRACCIÓN DE
EXPRESIONES ALGEBRAICAS
11
S/. a
S/. 2a
Ejemplo:
ADICIÓN Y SUSTRACCIÓN
Reducir:
M = 3a + b + 4a + 5b
Resolución:
Agrupamos y reducimos los términos semejantes:
M = (3a + 4a) + (b + 5b)
7a + 6b
Finalmente:
M = 7a + 6b
De nuestro ejemplo, tenemos que el costo para
comprar un borrador y lapicero es ...
a + 2a
3a
Por lo tanto, costará S/. 3a, este resultado se obtiene
sumando expresiones algebraicas.
¿Cuánto costará
comprar un borrador
y un lapicero?
Para saberlo,
debemos sumar los
precios del lapicero y
el borrador.
¿Cómo se efectúa la
adición y sustracción
de expresiones
algebraicas?
Se efectúa agrupando
los términos semejantes y
desarrollando las
operaciones indicadas.
Sabías que ...
El álgebra es, sobretodo,
una invención de los
árabes en el siglo IX y
AI- Juarismi es uno de los
grandes matemáticos
árabes que dio origen al
álgebra.
Sabías que ...

150. 4.° primaria
L U D O M A T I C
INGENIO
150
1
4
ANALIZAMOS Y APRENDEMOS
Reduce las operaciones:
A = 5a + 3a + 12a
B = 12a – 7a
Determina el valor de T = A + B.
Resolución:
a) Reducimos las operaciones en A y B.
b) Veamos
A = 5a + 3a + 12a
A = 8a + 12a
A = 20a
c) Comunicamos la respuesta.
Se pide reducir lo siguiente:
T = A + B
T = 20a + 5a
T = 25a
B = 12a – 7a
B = 5a
2 Calcula la suma de los lados del cua-
drado. Argumenta tu respuesta.
Resolución:
a)
Los lados del cuadrado tienen igual
medida; entonces, la suma será lo
siguiente:
P = 4x + 4x + 4x + 4x
P = 8x + 4x + 4x
P = 12x + 4x
P = 16x
4x
4x
4x
4x
4x
Completa los términos en la operación:
Resolución:
a) Completamos la primera operación.
Porque: 5a + 5a = 10a
b) Se baja el mismo valor.
c) Concluimos:
5a + 5a = 5a
10a
5a + 5a + 3a
10a + 3a
13a
5a + + 3a
10 a +
5a + 5a + 3a
10a + 3a
3 Si Telassim compra 2kg de camote y
3 kg de papa, ¿cuánto gasta en total?
Elabora tu estrategia de solución:
Resolución:
a) Planteamos una estrategia.
Calculamos lo que gasta en camote
y papa. Luego sumamos.
b) Ejecutamos la estrategia.
En camote gasta: a + a = 2a.
En papa gasta: b + b + b = 3b.
c) Comunicamos la respuesta.
En total, gasta: (2a + 3b) soles.
1 kg = S/. b
1kg = S/. a

151. L U D O M A T I C
INGENIO
Álgebra
151
Indicadores de evaluación
Realizo operaciones de adición y sustracción de
expresiones algebraicas.
Calculo el perímetro de figuras geométricas con
expresiones algebraicas.
Completo términos en una operación con expresiones
algebraicas.
Resuelvo problemas aplicando la adición y sustracción
con expresiones algebraicas.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Reduce las siguientes operaciones y
comunica tus respuestas.
T = 3x + 5x + 7x
E = 6y + 4x + 5x + 8y + 3x
L = 8ab + 3ab + 7ab
A = 8xy + 4x + 6xy + 5x + 2xy
S = 8a + 4b + 3ab + 9a + 5b + 3ab
Completa la operación:
+ 3a + 6a + 2a
10a +
Calcula la suma de los lados del
rectángulo. Argumenta tu respuesta.
Si Rocío gasta (3a + 4b) soles,
¿cuántos kilogramos compró
de cada producto. Elabora tu
estrategia de solución.
S/. a S/. b
1kg 1kg
2xy
6xy

152. 4.° primaria
L U D O M A T I C
INGENIO
152
OPERACIONES COMBINADAS DE
ADICIÓN Y SUSTRACCIÓN DE
EXPRESIONES ALGEBRAICAS
Ejemplo:
• Si hubiera signos de agrupación, primero desarrolla las operaciones en su interior
hasta eliminarlas.
Ejemplo:
•
Reduce la operación:
Q = 9ab – (3ab +4ab)
Resolución:
Q = 9ab – (3ab + 4ab)
Q = 9ab – 7ab
Q = 2ab
Se reduce de izquierda a derecha los
términos semejantes.
• Reduce la operación:
P = 20x – 5x – 3x – 4x
Resolución:
P = 20x – 5x – 3x – 4x
P = 15x – 3x – 4x
P = 12x – 4x
P = 8x
REDUCCIÓN DE OPERACIONES COMBINADAS
S/. 5x
S/. 3x
S/. 4x
•
De nuestro ejemplo, el dinero que le
queda después de la compra es...
20 x – (5 x + 4 x + 3 x)
20 x – (9 x + 3 x)
20 x – 12 x
8 x
Por lo tanto, le queda S/.8x.
TALLER
12
¿Cuánto dinero le
queda después de la
compra?
¿Cómo se reduce las
operaciones combinadas
de adición y sustracción de
expresiones algebraicas?
Con S/. 20x, compro
una pelota, un carrito
y una muñeca.
Reducimos los términos
semejantes de izquierda
a derecha.

153. L U D O M A T I C
INGENIO
Álgebra
153
Calcula el perímetro del rectángulo
mostrado. Argumenta tu respuesta.
Resolución:
a)
Completamoslamedidadeloslados
de la figura:
b) Su perímetro (P) es lo siguiente:
P = 5a + 5a + 3b + 3b
P = 10a + 6b
5a
3b
5a
3b
5a
3b
Completa los términos en la
operación:
Resolución:
a) Completamos el desarrollo de la
operación.
10x – + 6x – 2x
2x + 6x –
– 2x
10x – + 6x – 2x
2x + 6x –
– 2x
2x
8x
8x
6x
4. Elizabeth tiene 10a muñecas, a su
hermana le regala 2a y, por esta
buena acción, su mamá le da 3a
muñecas. ¿Cuántas muñecas tiene
ahora? Elabora tu estrategia de
solución.
Resolución:
a) Analizamos el problema.
Al principio, tiene 10a muñecas.
• Cuando regala 2a, le quedan
10a – 2a = 8a muñecas.
•
Cuando su mamá le regala 3a,
ahora le quedan:
8a + 3a = 11a muñecas.
b) Ahora, tiene 11a muñecas.
Reduce las operaciones:
A = 10x + 6x – 4x – 2x
B = 15x – 10x + 6x – 2x
y calcula el valor de M = A + B.
Resolución:
a) Reducimos A y B.
A = 10x + 6x – 4x – 2x
A = 16x – 4x – 2x
A = 12x – 2x
A = 10x
B = 15x – 10x + 6x – 2x
B = 5x + 6x – 2x
B = 11x – 2x
B = 9x
b) Se pide calcular lo siguiente:
M = A + B
M = 10x + 9x
M = 19x
1 2
3 4
ANALIZAMOS Y APRENDEMOS

154. 4.° primaria
L U D O M A T I C
INGENIO
154
Completa los términos en la siguiente
operación:
14x – + 5x – 8x
12x + 5x –
– 8x
Indicadores de evaluación
Reduzco operaciones combinadas de adición y
sustracción de expresiones algebraicas.
Completo los términos de una operación combinada
de adición y sustracción de expresiones algebraicas.
Resuelvo problemas, aplicando las operaciones
combinadas de adición y sustracción de expresiones
algebraicas.
AUTOEVALUACIÓN
1
PIENSO Y RESUELVO
3
2
4
Reduce las operaciones:
A = 18x + 8x – 10x – 4x
B = 16x – 8x + 6x – 12x
C = 5ab – 2ab + 8ab – 5ab
D = 12xy – 5xy – 2xy + 4xy
Calcula la suma de los lados de la
figura.
3y
2x
y y
x
Una caja tiene 30x canicas y otra,
tiene 20x. De cada caja, se retira
8x canicas. Luego, las canicas so-
brantes las depositan en una bolsa.
¿Cuántas canicas hay en la bolsa?
Elabora tu estrategia de solución.

155. EN EL MERCADO
PROYECTO DE APRENDIZAJE N.0
5
INGENIO
1.ª etapa 2.ª etapa
Elaboran varios billetes de S/. a, S/. 2a
y S/. 5a.
Llevan bolsas vacías de arroz y azúcar,
así como botellas de aceite vacías.
Elaboran los carteles con los precios
de los productos.
Los estudiantes deben especificar
la cantidad de dinero que tienen
y deben realizar una lista de los
productos y las cantidades que van
a comprar.
En el aula, se debe simular un mercado
donde los estudiantes deben realizar
las compras, según lo que han
especificado.
Deben presentar un informe del
balance de su compra, detallando lo
siguiente:
- Cantidad inicial de dinero.
- Cantidad de productos y precios.
– Gasto y vuelto de la compra.
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1. Situación problemática
Las operaciones con expresiones algebraicas están
presentes en nuestro quehacer diario. Al realizar una compra
o al pagar una deuda, realizamos este tipo de operaciones.
2. Finalidad
Simularemos una situación de compra y venta en un
mercado con billetes y precios creados por nosotros mismos.
Los estudiantes realizarán operaciones con expresiones
algebraicas y harán el presupuesto de la compra a realizar.
3. Recursos materiales
Billetes de cartulina de S/. a ; S/. 2a y S/. 5a. (Ver fig. 1).
Fotografías de papa, arroz, azúcar y aceite y sus
precios. (Ver fig. 2).
4. Etapas y actividades
S/. 12a
S/. 7a S/. 9a
S/. a
S/. 2a
S/. 5a
Billetes
fig. 1
fig. 2
155

156. UNIDAD
6
Educación en valores
OPERACIONES
CON EXPRESIONES
ALGEBRAICAS II
Cultivamos valores
•
Educación en valores y
formación ética.
• Tolerancia.
Aprendemos a:
•
Realizar diferentes tipos de multiplicación con
monomios.
•
Reducir operaciones con multiplicaciones de
monomios.
• Resolver problemas de diferentes contextos
que impliquen el uso de la multiplicación de
monomios.
Observa la imagen y contesta.
¿Qué son los valores?
¿Qué valores practicas en casa y en el colegio?
¿Por qué son importantes los valores en nuestra convivencia diaría?

157. L U D O M A T I C
INGENIO
Álgebra
157
LABORATORIO
6
1. Cada jugador lanza un dado. El que ob-
tenga el número de mayor puntaje inicia
el juego.
2.
El jugador que inicia, lanza los dos dados.
Los resultados los suma y multiplica. Si
obtiene las cantidades que figuran en
una tarjeta, se queda con ella y continúa
jugando. Si obtiene resultados que no
están en las tarjetas, le cede el turno al
otro jugador.
3. Continuan jugando hasta que no queden
más tarjetas.
Gana el juego el que
tenga más tarjetas en su
poder.
A
Producto
Producto
Producto
Producto
Suma
Suma
Suma
Suma
12
8
B
10
7
C
6
5
D
30
11
G A N AM O S
T A RJ E T A S
Nos organizamos
Jugamos y aprendemos
1. Nos agrupamos en parejas para iniciar el juego.
2. Recortan tarjetas como las mostradas en la
derecha.
3.
Cada pareja de jugadores debe traer 2 dados.

158. INGENIO
158
MULTIPLICACIÓN DE UN
NÚMERO POR UN POLINOMIO
¿Cómo multiplicamos
un número por un
monomio?
Se multiplica el número
y el coeficiente del
monomio, y se coloca
la misma parte literal.
6(5a) = (6×5)a
= 30a
Se multiplica el número y el
coeficiente del monomio.
Se coloca la misma
parte literal.
Multiplicación de un número por un polinomio
En este caso, el monomio multiplica a cada uno de los términos del polinomio.
Veamos:
4(5x + 3y) = 4(5x) + 4(3y)
= (4×5)x + (4×3)y
= 20x + 12y
número
polinomio
MULTIPLICACIÓN DE UN NÚMERO POR UN MONOMIO
S/. 5a
De nuestro ejemplo, al comprar 6 bolsas, el costo se obtiene así:
Por lo tanto, cuesta S/.30a.
Si yo quiero comprar
6 bolsas, ¿cuánto me
cuestan?
¿Cuánto cuestan 4
bolsas de caramelos
como los de la figura?
13
TALLER

159. L U D O M A T I C
INGENIO
Álgebra
159
Argumenta y determina el valor de
verdad de las siguientes proposiciones:
I. 3(2xy) = 6x + 3y ( )
II. 4(3x2
) = 12x2
( )
III. 5(3x + y) = 15xy ( )
Resolución:
a) Analizamos cada caso.
I. Es falso: porque:
3(2xy) =(3)(2)xy = 6xy.
II. Es verdadero: porque:
4(3x2
) = (4)(3)x2
= 12x2
III. Es falso: porque:
5(3x + y) = 5(3x) + 5y = 15x + 5y
b) Los valores son FVF respectivamente.
Calcula el valor de la operación:
M = 5(2x) + 3(2x) – 6(2x)
Resolución:
•
Multiplicamos cada número por su
respectivo monomio.
M = 5(2x) + 3(2x) – 6(2x)
M = 10x + 6x – 12x
• Reducimos.
M = 10x + 6x – 12x
16x – 12x
4x
• Por lo tanto, M = 4x.
Telassim compra “3x” chocolates y “4x”
caramelos. Elabora una estrategia y
determina una expresión que represente
el gasto hecho por Telassim.
Resolución:
a) Elaboramos una estrategia.
Debemos encontrar lo que se gasta
en chocolates y caramelos. Luego,
sumar los resultados.
b) Ejecutamos la estrategia.
• En chocolates, gasta 2(3x) = 6x soles.
•
En caramelos, gasta 3(4x) = 12x
soles.
c) Comunicamos la respuesta.
• En total, gasta 6x + 12x = 18x soles.
S/. 2
S/. 3
Utiliza la multiplicación de polinomios
y completa las siguientes igualdades:
Resolución:
a) Empleamos la multiplicación de
polinomios y tenemos lo siguiente:
• 6(3x2
y5
) = x y
• 5(3x+2y) = x + y
• 6(3x2
y5
) = (6x3) x2
y5
= 18x2
y5
= 18 x 2
y 5
• 5(3x+2y) = 5(3x) + 5(2y)
= 15x + 10y
= 15 x + 10 y
1 2
3 4
ANALIZAMOS Y APRENDEMOS

160. 4.° primaria
L U D O M A T I C
INGENIO
160
Si se sabe que:
2(5x2
y5
) = mxn
yp
Determina el valor de E = m + n x p
Indicadores de evaluación
Multiplico un número por un monomio o polinomio.
Calculo el valor de una operación, multiplicando
números por monomios o polinomios.
Resuelvo problemas con multiplicación de un número
por un monomio o polinomio
AUTOEVALUACIÓN
PIENSO Y RESUELVO
3 4 Elabora una estrategia de solución
para el siguiente problema: ¿Cuánto
gastará una persona si compra los
siguientes peluches:
3 tigres, 2 ositos y 4 gatitas?
S/. 3a S/. 2a S/. a
1 Multiplica y comunica tus resultados.
• 8(5xyz) • 3x(6x3
+ y2
)
• 3(9x) • 5x(4x + 3)
• 6(8x3
y) • 4(3x2
+ y2
)
2 Calcula el valor de A+B+C
Si:
A= 5(3x + 2x) + 3(2x)
B = 6(2x) – 5(2x)
C = 7(3x – x) + 4(2x)

161. INGENIO 161
Veamos:
Ejemplos:
Se suma los exponentes de las
variables comunes.
Se multiplica los
coeficientes.
(3x2
) (4x3
y) = (3)(4)x2+3
y = 12x5
y
■ (4x3
y5
)(3x2
y4
) = (4)(3)x3+2
y5+4
= 12x5
y9
■ (6a)(2a) = (6)(2)a1+1
= 12a2
■ (8xy)(2xy) = (8)(2)x1+1
y1+1
= 16x2
y2
MULTIPLICACIÓN DE MONOMIOS
2a
6a
En nuestro ejemplo, el área de la pizarra es la
siguiente:
(2a) (6a) = (2) (6)a1+1
= 12a2
MULTIPLICACIÓN DE UN
MONOMIO POR UN MONOMIO
¿Cómo calculamos
el área de la
pizarra de forma
rectangular?
El área de un
rectángulo es la
multiplicación de la
base por la altura.
¿Cómo se multiplica
un monomio por un
monomio?
Se multiplica los coeficientes de
los monomios y se acompaña
de las variables. En el caso de
las variables comunes, se escribe
una sola de ellas y se suma sus
exponentes.
Recuerda
Cuando no se escribe
el exponente de la
variable, se sobre-
entiende que es uno.
14
TALLER

162. 4.° primaria
L U D O M A T I C
INGENIO
162
(5x4
y )(2x y5
) = x7
y8
Calcula el valor de la expresión:
Resolución:
a) Multiplicamos los monomios:
K = (3)(4)x 2 + 2
+ 6x4
K = 12x4
+ 6x4
b) Sumamos los términos semejantes:
K = 12x4
+ 6x4
K = 18x4
K = (3x2
)(4x2
)+6x4
Supongamos que los lados de un
terreno rectangular miden 3x2
y 4x3
.
Determina su área y elabora una
estrategia de solución.
Resolución:
a)
Elaboramos una estrategia de
solución.
Debemos aplicar la fórmula para
calcular el área de un rectángulo.
b) Ejecutamos la estrategia.
El área es lo siguiente:
A = (base) x (altura)
A = (3x2
)(4x3
) = (3.4) x2+3
A= 12x5
c) Comunicamos la respuesta.
El área del rectángulo es 12x5
.
3x2
4x3
1 2
3 4
ANALIZAMOS Y APRENDEMOS
Argumenta y califica como verdadero
o falso las siguientes proposiciones:
I. (4x2
)(3y5
) = 12x2
y5
( )
II. (2x)(3x)(4x) = 24x ( )
III. (5x)(10x) = 50x2
( )
IV. (4x2
)(5x4
) = 20x6
( )
Resolución:
a) Analizamos cada caso:
II. (4x2
)(3y5
) = 12x2
y5
( V )
II. (2x)(3x)(4x) = 24x3
≠ 24x ( F )
III. (5x)(10x) = 50x2
( V )
IV. (4x2
)(5x4
) = 20x6
( V )
b) Por lo tanto, la respuesta es VFVV.
Utiliza la multiplicación de monomios y
calcula la suma de los números que
van en los recuadros.
Resolución:
a)
Analizamos la operación por partes.
■ Del coeficiente:
(5)x(2) = = 10
■ De los exponentes de X
4 + = 7 = 3
■ De los exponentes de y
+ 5 = 8 = 3
b) La operación queda como:
(5x4
y 3
) (2x 3
y5
) = 10 x7
y8
c)Porlotanto,lasumadelosnúmerosde
los recuadros es la siguiente:
= 3 + 3 + 10
= 16

163. L U D O M A T I C
INGENIO
Álgebra
163
4
3
Si las figuras están distribuidas en forma
rectangular, determina el área de
cada una de las piezas que lo
forman.
En el interior del terreno rectangular se
encuentra escrito su área. Determina
los valores de a, b y c.
6x
6x
2x
8x
7x
3x
ax2
y3
4xy2
12xb
yc
PIENSO Y RESUELVO
1 Multiplica los siguientes monomios:
■ (5x2
y5
) (3x2
y4
)
■ (3x5
) (6x7
)
■ (5xy) (3xy2
)
2
Si se cumple la operación:
(3x2
ya
) (bx3
y3
) = 15 xc
y9
Determina el valor dado:
P = a + b + c
Indicadores de evaluación
Multiplico monomios por polinomios.
Determino el valor de operaciones con multiplica-
ción de monomios.
Resuelvo problemas aplicando la multiplicación
de monomios.
AUTOEVALUACIÓN

164. INGENIO
164
¿Cómo se multiplica
un polinomio por un
monomio?
Veamos
Ejemplos:
■ (4x3
+ 5)(3x) = (4x3
)(3x) + (5)(3x) = 12x4
+ 15x
■ (7x + 3)(5x) = (7x)(5x) + 3(5x) = 35x2
+ 15x
■ (8x + 2y)(2xy) = (8x)(2xy) + 2y(2xy) = 16x2
y + 4xy2
MULTIPLICACIÓN DE UN POLINOMIO POR UN MONOMIO
3x + 2
2x
Se multiplica el primer término del
polinomio por el monomio.
Se multiplica el segundo término del
polinomio por el monomio.
(5x2
+ 4) (3x4
) = (5x2
)(3x4
) + (4)(3x4
)
= (5×3) x2+4
+(4×3)x4
= 15 x6
+ 12x4
MULTIPLICACIÓN DE UN
POLINOMIO POR UN MONOMIO
¿Cuál será el área
del rectángulo?
Humm...
Bastará con multiplicar
(3× + 2) y (2x); pero,
¿cómo se hace?
Se multiplica cada
término del polinomio
por el monomio.
15
TALLER

165. L U D O M A T I C
INGENIO
Álgebra
165
Argumenta y califica como verdadero
o falso las siguientes proposiciones:
I. (4x2
+5)(6x)= 24x3
+ 30x ( )
II. (2x + 3y)(4) = 8x + 12y ( )
III. (5a + 10b) = 50ab ( )
IV. (4x2
+ 5x4
)(2x) = 8x3
+ 10x5
( )
Resolución:
a)
Analizamos cada caso de
multiplicación de un polinomio por
un monomio.
I. (4x2
+5)(6x)= 24x3
+ 30x ( V )
II. (2x + 3y)(4) = 8x + 12y ( V )
III. (5a + 10b) ≠ 50ab ( F )
IV. (4x2
+ 5x4
)(2x) = 8x3
+ 10x5
( V )
b) Por lo tanto, el valor de verdad de las
proposiciones es VVFV.
Calcula el valor (x + y), de
Resolución:
a) Si multiplicamos se tiene lo siguiente:
b) Comparamos con el dato:
entonces:
x = 6 ; y = 4
c) Finalmente, nos piden la suma:
x + y = 6 + 4
=10
(3a3
+ 2a4
) (2a2
) = xa5
+ ya6
(3a3
+2a4
)(2a2
)=(3a3
)(2a2
)+(2a4
)(2a2
)
= 6a5
+ 4a6
xa5
+ ya6
= 6a5
+ 4a6
Supongamos que los lados de una
pizarra rectangular miden 5 + 2x2
y
2x3
. Determina su área y elabora una
estrategia de solución.
Resolución:
a) Debemos aplicar la fórmula para
calcular el área de un rectángulo.
b) Ejecutamos la estrategia.
El área es la expresión:
A = (base) × (altura)
A = (5 + 2x2
)(2x3
)
A = 10x3
+4x5
c) Comunicamos la respuesta.
El área de la pizarra es (10x3
+4x5
)u2
.
2x3
5 + 2x2
6 7
1 2
3 4
ANALIZAMOS Y APRENDEMOS
(5x4
+ 2x5
) (2x2
) = x + 4x
Utiliza la multiplicación de un polinomio
por un monomio y calcula la suma de
los números que van en los recuadros.
Resolución:
a) Desarrollamos la operación:
(5x4
+ 2x5
)(2x2
) = (5x4
)(2x2
) + (2x5
)(2x2
)
= (5)(2) x4+2
+(2)(2) x5+2
= 10 x6
+ 4x7
= 10 x + 4x
b) Se pide:
10 + 6 + 7 = 23

166. 4.° primaria
L U D O M A T I C
INGENIO
166
PIENSO Y RESUELVO
2
4
Al comprar 4 peluches como el
mostrado, ¿cuánto se gastó?
Elabora tu estrategía de solución.
s/.3x+4
Un libro cuesta S/. (2x + 5). Si se
compra 3 de estos libros, ¿cuánto
se gastará?.
Elabora tu estrategía de solución.
1
Multiplica y compara las respuestas
con las de tus compañeros.
• (3a2
+ 5a4
) (3a4
)
• (3x2
+ 7) (4x3
)
• (2a2
– a4
) (4)
• (5a5
+ 4a) (2a)
3. Si:
Calcula el valor de M = A + B.
A= (3x + 4x3
) (2x)
B= 5x2
+ 8x4
3
Indicadores de evaluación
Multiplico un polinomio por un monomio.
Determino el valor de las operaciones con
multiplicación de polinomio por monomios.
Resuelvo problemas aplicando la multiplicación de
un polinomio por un monomio.
AUTOEVALUACIÓN

167. COMPRAMOS ARTEFACTOS
PROYECTO DE APRENDIZAJE N.0
6
INGENIO
1. Situación problemática
Recrear en el aula situaciones de la vida cotidiana nos
ayuda a entender cómo la matemática está presente en
todo momento y en todo lugar. Por ejemplo, la aplicación
de la multiplicación de monomios nos permite abreviar
operaciones de compra y venta.
2. Finalidad
•
Aplicar la multiplicación de expresiones algebraicas al
recrear una situación de compra de un producto.
•
Concientizar a los estudiantes acerca de la importancia
de aplicar los conocimientos matemáticos a situaciones
de nuestra vida cotidiana.
3. Recursos materiales
Periódicos, revistas, goma
Papelote, plumones, tijera, regla
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1.ª etapa 2.ª etapa
Organícense en equipos de 4
integrantes.
Elijan tres productos, busquen
fotos de artefactos en el
periódico o revistas, recórtenlas y
péguenlas en su papelote.
A cada producto pónganle un
precio en función de “x”; por
ejemplo: S/. 20x.
Elijan comprar una cantidad
determinada de cada producto y
calculen el costo que demandaría
la compra total.
Realicen sus operaciones en
el papelote y expongan sus
resultados en la clase.
Peguen sus trabajos en las paredes
del aula.
167

168. Observa la imagen y contesta.
UNIDAD
7
Aprendemos a:
Cultivamos valores
Educación en equidad de géneros
¿Sabes qué es la igualdad de géneros?
¿Hombres y mujeres tienen las mismas oportunidades?
•
Educación para la
equidad de géneros.
• Tolerancia.
• Identificarlasdiferentesformasdeecuaciones.
•
Resolver ecuaciones de la forma x + a = b;
x - a = b; ax = b; x/a = b; a x + b = c; a x - b = c.
• Interpretar y plantear ecuaciones.
• Resolver problemas de diferentes contextos
que impliquen el uso de las ecuaciones.

169. L U D O M A T I C
INGENIO
Álgebra
169
Jugamos y Aprendemos
Nos organizamos
TRANSFORMAMOS
NÚMEROS
7
1. Formen parejas.
2. Reproduzcan el diagrama de la derecha en
varias hojas.
3. Cada integrante debe tener 3 hojas con sus
respectivos diagramas. Cada hoja, será
utilizada en una partida. El juego consta de 3
partidas.
1. Para iniciar una partida, cada integrante toma
un diagrama e introduce un número menor
que 20; luego, se lo entrega al otro compañero
para que lo resuelva. Los diagramas deben
estar volteados.
2.Al mismo tiempo, ambos dan vuelta al
diagrama y comienzan a resolverlo. El que
termina primero con la resolución correcta
gana la partida.
3. Repiten el proceso con los diagramas restantes
hasta completar el juego.
Introduzca
un número
Sume 6
Reste 4 Multiplique
por 2
Reste el número
que introdujo
El resultado es ...
Gana el juego el
que gana al
menos dos
de las 3 partidas.
LABORATORIO

170. 4.° primaria
L U D O M A T I C
INGENIO
170
Veamos
×
10 cm
50 cm
Variable o incógnita
x + 10 = 50
Primer
miembro
Segundo
miembro
x + 10 = 50
x = 50 – 10
x = 40
Pasa a restar al otro miembro.
NOCIÓN DE ECUACIÓN
RESOLUCIÓN DE UNA ECUACIÓN DEL TIPO: x + a = b
El valor de “a” que está sumando en el primer miembro pasa al otro miembro restando.
Se opera obteniendo el valor “x”.
x = b – a
Ejemplo
Resuelve la siguiente expresión: x + 10 = 50.
Resolución:
ECUACIONES DE LA FORMA
TALLER
16 x + a = b ; x - a = b;
ax = b ; x /a = b
El tamaño del arbolito
se puede determinar al
resolver la expresión:
x + 10 = 50
¿Cuánto mide
el arbolito?
¿Qué es una
ecuación?
Es una igualdad que se
verifica para un valor
determinado de la
variable o incógnita.
Importante :
Resolver una ecuación
esdeterminarelvalorde
la variable o incógnita.

171. L U D O M A T I C
INGENIO
Álgebra
171
x – 20 = 40
x = 40 + 20
x = 60
Pasa a sumar al otro miembro.
RESOLUCIÓN DE UNA ECUACIÓN DEL TIPO: x – a = b
El valor de “a”, que está restando en el primer miembro, pasa al otro miembro suman-
do. Se opera obteniendo el valor de “x”.
x = b + a
Ejemplo:
Resuelve x – 20 = 40.
Resolución:
RESOLUCIÓN DE UNA ECUACIÓN DEL TIPO: ax = b
El valor de “a”, que está multiplicando en el primer miembro, pasa al otro miembro
dividiendo. Se opera obteniendo el valor de “x”.
x =
Ejemplo:
Resuelve 4x = 20.
Resolución:
b
a
Pasa a dividir al otro miembro.
4x = 20
x =
x = 5
20
4
a
x
Pasa a multiplicar al otro miembro.
3
RESOLUCIÓN DE UNA ECUACIÓN DEL TIPO: = b
El valor de “a”, que está dividiendo en el primer miembro, pasa al otro miembro
multiplicando. Se opera obteniendo el valor de “x”.
x = b × a
Ejemplo:
Resuelve
Resolución:
= 4.
x
x = (3) (4)
x = 12
3
= 4
x

172. 4.° primaria
L U D O M A T I C
INGENIO
172
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Si a – 3 = 5, determina el valor de “x”
en la ecuación: x + a = 12. Comunica
tu respuesta.
Resolución:
a) Primero, calculemos el valor de “a”.
a – 3 = 5
a = 5 + 3
a = 8
b) Reemplazamos el valor de “a” en la
ecuación y desarrollamos.
x + a = 12
x + 8 = 12
x = 12 – 8
x = 4
c) El valor de “x” es 4.
Si 3a = 12, calcula el valor de “x” en el
dato: Argumenta tu respuesta.
Resolución:
a) De la primera ecuación, calculamos
el valor de “a”.
3a = 12
a =
12
a = 4
3
b) Reemplazamos el valor de “a” en la
segunda ecuación.
c) El valor de “x” es 8.
x
2
= a.
= 4
= a
x
2
x
2
x = (2) (4) x = 8
Completa el número en el recuadro:
Representa la ecuación.
Resolución:
a) Supongamos que el número del
recuadro es “x”; entonces, se forma
una ecuación:
x + 5 = 4 + 7
b) Resolvemos la ecuación para
obtener el valor de “x”.
x + 5 = 11
x = 11 – 5
x = 6
c) Por lo tanto, el número que debe
ir en el recuadro es el 6, siendo la
ecuación que se forma:
x + 5 = 4 + 7
+ 5 = 4 + 7
De la balanza en equilibrio, determina
el peso de cada bolsa de arroz.
Elabora tu estrategia de solución.
Resolución:
a) Planteamos una estrategia.
El peso de cada platillo es igual; por
lo tanto, planteo una ecuación,
donde “x” representa el peso de
una bolsa de arroz.
b) Ejecuta la estrategia.
La ecuación es 3x = 15.
Desarrollamos.
3x = 15
x =
15
3
x = 5
c) Comunicamos la respuesta
“Cada bolsa de arroz pesa 5 kg”.
15 kg

173. L U D O M A T I C
INGENIO
Álgebra
173
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Resuelvo ecuaciones de la forma: x+a = b ; x – a = b.
Determino ecuaciones de la forma: ax = b ; x/a = b.
Completo números formando ecuaciones.
Determino el valor de “x” resolviendo ecuaciones
previas.
Las tarjetas que acompañan a cada
peluche representan su precio, pero
un valor ha sido escondido.
Determina dicho valor en cada caso.
S/. 2
s/.a – 7
s/.x + 4
S/. 10
s/.4y
S/. 32
S/. 3
b
5
s/.
He comprado 3 libros y en total gasté
100 Nuevos Soles. Determina el precio
del libro que falta. Elabora tu estrategia
de solución.
S/. 25
S/. 42
S/. x
Si + 5 = 12
además 2 + = 15
Determina el valor de
Elabora tu estrategia de solución.
Determina el número que debe ir
en cada recuadro. Represéntalo en
ecuación.
■ + 4 = 15
■ – 2 = 7
■ 5 × = 45
■ _____
3
= 2

174. 4.° primaria
L U D O M A T I C
INGENIO
174
8 kg
3 kg
ECUACIÓN DE LA FORMA: ax + b = c
3x + 2 = 11
3x = 11 – 2
3x = 9
__
3
9
x = x = 3
Pasa a restar al otro
miembro.
Pasa a dividir al
otro miembro.
ECUACIÓN DE LA FORMA: ax – b = c
Para resolverla, el valor de “b”, que está restando en el primer miembro, pasa al otro
miembro a sumar el valor de “c”. Luego, el valor de “a” pasa a dividir. Se opera,
obteniendo el valor de “x”.
Ejemplo:
2x – 4 = 8
2x = 8 + 4
2x = 12
x = x = 6
12
2
Pasa a sumar al otro
miembro.
Pasa a dividir al
otro miembro.
Resuelve 2x – 4 = 8.
Resolución:
Resuelve la ecuación de nuestro ejemplo.
Resolución:
Cada papaya pesa 3kg.
ECUACIONES DE LA FORMA
TALLER
17 ax + b = c ; ax - b = c
¿Cuánto pesa cada
papaya si todas tienen el
mismo peso y la balanza
está equilibrada?
El valor de “b”, que está
sumando en el primer
miembro, pasa al otro a restar
a “c”. Luego, el valor de “a”
pasa a “dividir”, se opera y se
obtiene el valor de “x”.
¿Cómo se resuelve
una ecuación del
tipo ax + b = c?
El peso de cada papaya
se puede determinar al
resolver la ecuación:
3x + 2 = 11, donde “x”
representa el peso
de cada papaya.
2 kg

175. L U D O M A T I C
INGENIO
Álgebra
175
ANALIZAMOS Y APRENDEMOS
1 Si 2a – 5 = 9, determina el valor de “x”
en la ecuación: x + a = 10.
Resolución:
a) Desarrollamos la primera ecuación
para obtener el valor de “a”.
2a – 5 = 9
2a = 9 + 5
2a = 14
a
= 14 a = 7
2
b) Reemplazamos el valor de “a” en la
segunda ecuación y despejamos el
valorde “x”.
x + a = 10
x + 7 = 10
x = 10 – 7
x = 3
c) Por lo tanto, el valor de “x” es 3.
4 De la balanza en equilibrio, calcula el
peso de cada bolsa de arroz.
Resolución:
a) El peso de cada platillo es igual; por
lo tanto, planteo una ecuación,
donde “x” representa el peso de
una bolsa de arroz.
b) Determinamos la ecuación:
2x + 2 = 8 + 6
■ Desarrollamos.
2x + 2 = 14
2x = 14 – 2
2x = 12
x =
12
x = 6
2
c) Por lo tanto, cada bolsa de arroz
pesa 6 kg.
8 kg
2kg 6 kg
Del siguiente rectángulo, calcula el
valor de “x”. Elabora tu estrategia de
solución.
Resolución:
a) Los lados opuestos de un rectángulo
son iguales; entonces:
■ 5a – 1 = 9
5a = 9 + 1
5a = 10
a =
10 a = 2
5
■ 3x – a = 16 (reemplazamos el valor
de “a”)
3x – 2 = 16
3x = 16 + 2
3x = 18
x =
18
x = 6
3
b) Por lo tanto, el valor de “x” es 6.
2
5a – 1 9
3x – a
16
3 Completa el número en el recuadro:
Representa la ecuación.
Resolución:
a) Suponiendo que el número del
recuadro es “x”; entonces, formamos
la ecuación: 4x + 5 = 17
b) Resolvemos:
4x + 5 = 17
4x = 17 – 5
4x = 12
x =
12 x = 3
4
c) El número que debe ir en el recuadro
es el 3 y la ecuación es 4x + 5 = 17.
4 + 5 = 17

176. 4.° primaria
L U D O M A T I C
INGENIO
176
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Resuelvo ecuaciones de la forma ax+b = c.
Calculo ecuaciones de la forma: ax – b = c.
Completo números formando ecuaciones.
Si los objetos iguales tienen el mismo
precio en soles, determina el valor
de x; y; z. Elabora tu estrategia de
solución.
S/.5y – 3
S/.4z + 12
S/.20
S/.7
S/.10
S/.2x + 4
Completa el número que debe ir en
cada recuadro. Represéntalo en la
ecuación.
■ 2 + 4 = 10
■ 3 – 2 = 7
■ 5 + 10 = 45
■ 6 – 6 = 6
Si: 2a – 3 = 5
5b + 2 = 7
Determina el valor de “x” en la
ecuación: x + b = a.
Si el lado del cuadrado es 7 cm,
calcula la suma de los lados del
rectángulo.
2x – 1
x
3x

177. L U D O M A T I C
INGENIO
Álgebra
177
Ejemplo:
TRADUCCIÓN DE EXPRESIONES VERBALES EN MATEMÁTICAS
Un número aumentado en cinco
x + 5
}
}
}
Expresión verbal
Expresión matemática
Un número aumentado en cinco : x + 5
PLANTEO DE ECUACIONES
Es convertir el enunciado de un problema en una ecuación y resolverlo.
De nuestro ejemplo:
Si al doble de mi edad, le sumo 5 años, se obtiene 25 años. Calcula mi edad.
}
}
}
}
}
2 x +5 = 25
Resuelvo la ecuación:
2x+5 = 25
2x = 25 – 5
2x = 20
x = 20
2
x = 10
Mi edad es 10 años.
PLANTEO DE ECUACIONES
TALLER
18
Si al doble de mi edad,
le sumo 5 años, se
obtiene 25 años.
¿Cuántos años
tiene ella?
¿En qué consisten
las traducciones de
expresiones verbales
a expresiones
matemáticas?
Consiste en traducir
una expresión verbal al
lenguaje matemático.

178. 4.° primaria
L U D O M A T I C
INGENIO
178
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Si a la edad de Telassim se le aumenta
6 años; entonces, tendría 16 años.
¿Cuántos años tiene Telassim?
Elabora tu estrategia de solución.
Resolución:
a) Identificamos la incógnita.
Edad de Telassim : x
b) Planteamos el problema.
Edad de Telassim : x
aumentada en 6 años : x+ 6
es igual a16 : x + 6 = 16
c) Resolvemos la ecuación:
x + 6 = 16
x = 16 – 6
x = 10
d) Comunicamos la respuesta.
La edad de Telassim es 10 años.
El doble del dinero que tiene Omar más
S/. 4 es igual al dinero que tiene Sonia.
¿Cuánto tiene Omar si Sonia tiene
S/. 40?. Elabora tu estrategia de solución.
Resolución:
a) Identificamos la incógnita.
Dinero que tiene Omar : x
b) Planteamos el problema.
El doble del dinero que tiene
Omar : 2x
más cuatro : 2x +4
es igual al dinero
que tiene Sonia : 2x + 4 = 40
c) Resolvemos la ecuación.
2x + 4 = 40
2x = 40 – 4
2x = 36
x = 36/2
x = 18
d) Comunicamos la respuesta.
El dinero que tiene Omar es de S/. 18.
La edad de Rocío es el cuádruple de
la edad de su hija Telassim. Si la suma
de las edades es 45 años, determina las
edades de cada uno de ellas y elabora
tu estrategia de solución.
Resolución:
a) Identificamos la incógnita.
Edad de Telassim : x
Edad de Rocío: 4x
b) Planteamos el problema.
La suma de sus edades es 45: x + 4x = 45.
c) Resolvemos la ecuación.
x + 4x = 45
5x = 45
x = 45/5
x = 9
d) Comunicamos la respuesta.
La edad de Telassim es 9 años.
La edad de Rocío es 4x = 4(9) = 36 años.
¿Cuál es el número que multiplicado
por 8 nos da 40? Elabora tu estrategia
de solución.
Resolución:
a) Identificamos la incógnita.
Sea el número : x
b) Planteamos el problema.
El número multiplicado por 8 nos da
40: 8x = 40.
c) Resolvemos la ecuación.
8x = 40
x = 40/8
x = 5
d) Comunicamos la respuesta.
El número es 5.

179. L U D O M A T I C
INGENIO
Álgebra
179
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Traduzco expresiones verbales al lenguaje
matemático.
Argumento la solución de problemas.
Resuelvo problemas con ecuaciones.
Traduce a lenguaje matemático las
siguientes expresiones:
a) El quintuplo de un número
b) Dos veces un número, aumentado
en 3.
c) La edad de una persona hace 6
años.
d) La edad de una persona dentro de
2 años.
El doble del dinero que tiene Omar
más S/. 6 es igual al dinero que tiene
Sonia. ¿Cuánto dinero tiene Omar si
Sonia tiene S/. 50? Elabora tu estrategia
de solución.
Si al doble de mi
edad le aumen-
tará 3 años...
... entonces
tendrías 23
años.
¿Cuántos
años tengo?
¿Cuál es el número que multiplicado
por 5 y su resultado, sumado con 10,
nos da 80? Elabora tu estrategia de
solución.

180. PROYECTO DE APRENDIZAJE N.0
7
LAS ECUACIONES EN LA VIDA DIARIA
INGENIO
1.ª etapa 2.ª etapa
Organícense en grupos de 4
estudiantes.
 Planteen un problema de
aplicación en la vida cotidiana que
sea resoluble por ecuaciones.
Busquen en revistas o periódicos las
palabras y dibujos que intervengan
en el problema.
Regan sus recortes en un papelote,
dando la forma de un problema.
Resuelven el problema, identificando, los
datos, la ecuación y la respuesta.
Los grupos sustentan el problema resuelto
en su papelote y los pegan en el interior
del aula.
1. Situación problemática
Sin duda alguna, las ecuaciones están presentes en diferentes
tipos de operaciones que realizamos. Son parte de nuestra
vida, por lo que debemos aprender a plantearlas y resolverlas.
2. Finalidad
• Plantear problemas con ecuaciones y resolverlas.
• Comprender la utilidad de las ecuaciones y su
presencia en nuestra vida cotidiana.
3. Recursos materiales
Periódicos, revistas. Papelotes.
Catálogos de productos. Tijeras.
Goma. Plumones.
4. Etapas y actividades
5. Evaluación
Si me dieran S/.2
más, podría comprar
ese polo que
cuesta S/.10.
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
180

181. Educación para el éxito
INECUACIONES
Cultivamos valores
•
Educación para el
éxito.
• Respeto.
Observa la imagen y contesta.
¿Qué entiendes por tener éxito?
¿Es necesario la perseverancia para lograr el éxito?
¿Qué debo hacer para triunfar en la vida?
Aprendiendo a:
• Identificar las diferentes formas de inecuaciones.
• Resolver diferentes tipos de inecuaciones.
• Interpretar y plantear inecuaciones.
• Resolver problemas de diferentes contextos que
impliquen el uso de las inecuaciones.
UNIDAD
8

182. 4.° primaria
L U D O M A T I C
INGENIO
182
1. Formen parejas para jugar.
2.
Reproduzcan el diagrama en una hoja de
papel.
3. Cada estudiante debe traer dos dados y
tener un diagrama como el mostrado.
1.
Para jugar una partida, en simultáneo cada
participante lanza sus dados y los coloca en
uno de los diagramas según los números que
haya obtenido. Quien los coloque de manera
correcta, en el menor tiempo posible, gana la
partida.
Por ejemplo:
Un participante lanza sus dados y obtiene 6 y
2; entonces los puede ordenar así:
2.
Si al lanzar los dados, obtiene los mismos
números, no los podrá colocar en ninguna de
las balanzas. Si el otro participante logra poner
correctamente sus dados, entonces gana la
partida.
3. Si al lanzar los dados ambos participantes
obtienen cantidades iguales, ninguno gana la
partida.
4. Para ganar el juego, un participante debe
ganar 3 partidas.
• Cuando el número del
primer platillo es mayor.
• Cuando el número del
primer platillo es menor.
o también
B A L A N C E AM O S
N Ú M E R O S
Nos organizamos
Jugamos y Aprendemos
8
LABORATORIO
182

183. L U D O M A T I C
INGENIO
Álgebra
183
INECUACIONES DE LA FORMA:
x + a b ; x + a b
Veamos lo siguiente:
Variable o incógnita
x + 12 15
Primer
miembro
Segundo
miembro
NOCIÓN DE INECUACIÓN
Es una desigualdad
que se verifica para un
conjunto de valores.
La inecuación mostrada se verifica para los
siguientes valores:
x = 0, entonces: 0 + 12 15
12 15, cumple.
x = 1, entonces: 1 + 12 15
13 15, cumple.
x = 2, entonces: 2 + 12 15
14 15, cumple.
x = 3, entonces: 3 + 12 15
15 15, no cumple.
El conjunto de valores que verifica la
desigualdad es {0; 1; 2}.
■ El símbolo: se lee “menor que”.
Ejemplo:
3 5, tres es menor que cinco.
■ El símbolo: se lee “mayor que”.
Ejemplo:
7 5, siete es mayor que cinco.
Analizo las
figuras para
determinarlas.
4 kg
6 kg
¿Cuánto pesa la
manzana si se sabe
que su peso es un
número natural?
¿Qué es una
inecuación?
Importante:
Resolver una inecuación
es encontrar el conjunto
de valores de la variable
o incógnita.
TALLER
19

184. 4.° primaria
L U D O M A T I C
INGENIO
184
Pasa a restar al otro miembro.
x + 2 6
x 6 – 2
x 4
C.S. = {0 ; 1 ; 2 ; 3} Su conjunto solución son todos los valores
menores que cuatro.
Si la inecuación fuera de la forma x – a b
Se resuelve igual solo que “a” pasa al segundo miembro a sumar.
Pasa a restar al otro miembro.
Su conjunto solución son todos los valores
mayores que seis.
x + 3 9
x 9 – 3
x 6
C.S. = {7; 8 ; 9; ...}
Si la inecuación fuera de la forma x – a b, se resuelve igual, solo
que “a” pasa al segundo miembro a sumar.
Una desigualdad de tres
partes se expresa de la
siguiente manera:
■ 3 4 6 : “4 es mayor que 3, pero menor que 6”.
■ 1 x 5 : “x es mayor que 1, pero menor que 5”.
RESOLUCIÓN DE UNA INECUACIÓN DEL TIPO: x + a b
El valor de “a”, que está sumando en el primer miembro, pasa al otro miembro restando.
El conjunto solución son todos los valores menores a dicha diferencia.
x b – a
Ejemplo:
Resuelve: x +2 6
Resolución:
RESOLUCIÓN DE UNA INECUACIÓN DEL TIPO: x + a b
El valor de “a”, que está sumando en el primer miembro pasa al otro miembro restando.
El conjunto solución son todos los valores mayores a, dicha diferencia.
x b – a
Ejemplo:
Resuelve x +3 9.
Resolución:

185. L U D O M A T I C
INGENIO
Álgebra
185
Si a – 2 = 5, determina el conjunto
solución de x + a 10. Comunica tu
respuesta.
Resolución:
a) De la ecuación, determinamos el
valor de “a”.
a – 2 = 5
a = 5 + 2
a = 7
b) Reemplazamos el valor de “a” en
la inecuación y desarrollamos.
x + a 10
x + 7 10
x 10 – 7
x 3
c) El conjunto solución es el siguiente:
{0 ; 1 ; 2}
Rosa tiene más de cuatro libros, pero
menos de 6. ¿Cuántos libros tiene Pedro
si tiene dos libros más que Rosa?
Resolución:
a) Planteamos la estrategia.
Encontremos la cantidad de libros que
tiene Rosa y luego determinamos lo de
Pedro.
b) Ejecutamos la estrategia.
- Sea “x” la cantidad de libros de Rosa.
- Rosa tiene más de 4 libros: x 4.
- Rosa tiene menos de 6 libros: x 6.
-
Como 4 x 6, su único valor natural
es 5.
- Por lo tanto, Rosa tiene 5 libros.
c) Como Pedro tiene 2 libros más que Rosa,
entonces:
Pedro tiene 5 + 2 = 7 libros.
1
Completa el mayor número natural que
debe ir en el recuadro:
Representa la inecuación.
Resolución:
a) Supongamos que el número del
recuadro es “x”; entonces, se forma
la inecuación.
x + 3 4 + 5
b) Resolvemos la inecuación.
x + 3 9
x 9 – 3
x 6
c) Su conjunto solución es el siguiente:
{0; 1; 2; 3; 4; 5}
d) Por lo tanto, el mayor número
natural, que debe ir en el recuadro,
es 5 y su inecuación es x + 3 4 + 5.
+ 3 4 + 5
3 4
ANALIZAMOS Y APRENDEMOS
Si las manzanas tienen el mismo peso,
¿cuál es el mayor peso que puede
tener la pera? Elabora tu estrategia
de solución.
Resolución:
a) De la balanza en equilibrio, tenemos
que el peso de las 3 manzanas es igual
a 120 g. Entonces:
3 manzanas = 120
1 manzana =
1 manzana = 40
b) Una manzana pesa 40g.
c) De la balanza en desequilibrio se tiene
el dato:
pera manzana
pera 40
d) El mayor peso que puede tener una
pera es 39 g.
120 g
2
120
3

186. 4.° primaria
L U D O M A T I C
INGENIO
186
PIENSO Y RESUELVO
4 Se muestra una balanza donde cada
bloque indica su respectivo peso en
kilogramos.
Representa lo mostrado en la figura
como una inecuación y determina el
mayor peso entero del bloque
marcado con “x”.
x 4
6 2
1 Resuelve las siguientes inecuaciones
y comunica tus respuestas.
• x + 3 8
• x + 2 15
• x – 2 3
• x – 5 2
2
Si a – 2 = 3, determina el conjunto
solución de x + a 9.
Argumenta tu respuesta.
3 Si – 3 = 8
3 + = 8
Determina el conjunto solución de:
x +
Indicadores de evaluación
Resuelvo inecuaciones de la forma x + a b.
Determino inecuaciones de la forma: x + a b.
Completo números formando inecuaciones.
Encuentroelconjuntodevaloresde“x”,resolviendo
inecuaciones.
AUTOEVALUACIÓN

187. L U D O M A T I C
INGENIO
Álgebra
187
2 x + 4 12
2x 12 – 4
2x 8
C.S = {0 ; 1 ; 2 ; 3}
Ejemplo:
INECUACIÓN DE LA FORMA: ax + b c
Pasa a dividir al
otro miembro.
8
2
4
x
x
Pasa a restar al otro
miembro.
Su conjunto solución son todos los
valores menores a cuatro.
Resuelve 2x + 4 12.
Resolución:
6kg
10kg
INECUACIONES DE LA FORMA :
ax + b c; ax – b c ; ax + b c ; ax – b c
¿Cuánto pesa la esfera
si se sabe que es un
número natural?
Observa bien los
dibujos y podrás llegar
a la respuesta.
¿Cómo se resuelve
una inecuación del
tipo ax + b c?
El valor de “b”, que está en el primer
miembro, pasa al otro miembro restando.
Luego, el valor de “a” pasa a dividir.
El conjunto solución son todos los valores
menores a dicho cociente.
INECUACIONES DE LA FORMA: ax – b c
El valor de “b”, que está restando en el primer miembro, pasa al otro miembro sumando.
Luego, el valor de “a” pasa a dividir.
El conjunto solución son todos los valores menores que dicho cociente.
TALLER
20

188. 4.° primaria
L U D O M A T I C
INGENIO
188
3× + 9 12
3x 12 – 9
3x 3
C.S = {2 ; 3; 4; ...}
INECUACIONES DE LA FORMA: a x + b c
El valor de “b”, que está sumando en el primer miembro, pasa al otro restando.
Luego, el valor de “a” pasa a dividir.
El conjunto solución son todos los valores mayores a dicho cociente.
Ejemplo:
Resuelve 3x + 9 12.
Resolución:
Pasa a restar al otro
miembro.
Su conjunto solución son todos los
valores mayores que 1.
Pasa a dividir al
otro miembro.
3
3
1
x
x
3x – 1 11
3x 11 + 1
3x 12
C.S = {0 ; 1 ; 2 ; 3}
12
3
4
x
x
Pasa a sumar al otro
miembro.
Su conjunto solución son todos los
valores menores que cuatro.
Pasa a dividir al
otro miembro.
INECUACIONES DE LA FORMA: a x – b c
El valor de “b”, que está restando en el primer miembro, pasa al otro miembro sumando.
Luego, el valor de “a” pasa a dividir.
El conjunto solución son todos los valores mayores a dicho cociente.
Ejemplo:
Resuelve 3x – 9 12.
Resolución:
Pasa a sumar al otro
miembro.
Su conjunto solución son todos los
valores mayores que 7.
Pasa a dividir al
otro miembro.
21
3
7
x
x
3x – 9 12
3x 12 + 9
3x 21
C.S = {8 ; 9; 10; ...}
Ejemplo:
Resuelve 3x – 1 11.
Resolución:

189. L U D O M A T I C
INGENIO
Álgebra
189
1. Si a – 1 = 4, determina el conjunto
solución de 2x + a 9. Comunica tu
respuesta.
Resolución:
a)
De la ecuación, determinamos el
valor de “a”.
a – 1 = 4
a = 4 + 1 a = 5
•
Reemplazamos el valor de “a” en la
inecuación y desarrollamos.
2x + 5 9
2x 9 – 5
2x 4
x 4/2
x 2
b)
Por lo tanto, el conjunto solución es
el siguiente:
{0; 1}
Si al triple de las muñecas que tiene
Ana le agregan 4, se obtiene una
cantidad menor que 22. ¿Cuál es la
mayor cantidad de muñecas que
podría tener Ana? Elabora tu
estrategia de solución.
Resolución:
a) Planteamos la estrategia.
Hay que plantear la inecuación y
determinar su conjunto solución.
b) Ejecutamos la estrategia.
• Cantidad de muñecas de Ana: x
• El triple de las muñecas: 3x
• Le agregan 4: 3 x + 4
• Cantidad menor que 22: 3 x + 4 22
c) Resolvemos la inecuación.
3 x + 4 22
3x 22 – 4
3x 18
x 18/3
x 6
C.S = {0; 1; 2; 3; 4; 5}
d) Comunicamos la respuesta.
La mayor cantidad de muñecas que
puede tener Ana es 5.
4
ANALIZAMOS Y APRENDEMOS
Si la figura muestra la cantidad de
plátanos que compró una persona,
se sabe que gastó menos de 12 soles.
¿Cuánto cuesta comó máximo un
plátano? Elabora tu estrategia de
solución.
Resolución:
a) Supongamos que cada plátano cuesta
S/. x. Al comprar 3 plátanos, se gasta 3x
Nuevos Soles.
b) Como gastó menos de 12 Nuevos Soles,
se tiene lo siguiente: 3x 12
c) Resolvemos la inecuación:
x x 4
El conjunto solución es el siguiente:
{0; 1; 2; 3}
d) Un plátano cuesta como máximo 3 Nue-
vos Soles.
2
12
3
Completa el mayor número natural
que debe ir en el recuadro:
Representa la inecuación.
Resolución:
a) Supongamos que el número del
recuadro es “x”; entonces, se forma
una inecuación.
2x + 3 11
b) Resolvemos la inecuación.
2x + 3 11
2x 11 – 3
2x 8
x
x 4
Su conjunto solución es el siguiente:
{0; 1; 2; 3}
c) Por lo tanto, el mayor número natural
que debe ir en el recuadro es 3 y la
inecuación es 2x + 3 11.
2 + 3 11
3
8
2
1

190. 4.° primaria
L U D O M A T I C
INGENIO
190
PIENSO Y RESUELVO
3 4
Con los valores de a y b de los
cuadrados.
Determina el conjunto solución de la
inecuación:
2x + a b
a + 1 b + 3
4
18
Se muestra una balanza donde cada
bloque indica su respectivo peso en
kilogramos.
Representa lo mostrado en la figura
como una inecuación y determina
el mayor peso del bloque marcado
con “x”.
x 4
10 2
x
1. Resuelve las siguientes inecuaciones y
comparte tus respuestas con tus
compañeros.
• 2x + 5 13 • 3x – 2 13
• 3x + 2 17 • 2x + 5 25
1 2 Si – 2 = 4, determina el conjunto
solución del siguiente dato:
2x + 24
Indicadores de evaluación
Resuelvo inecuaciones de la forma ax + b c ; ax – b c
Determino inecuaciones de la forma ax + b c ; ax – b c
Completo números formando inecuaciones.
Determino el conjunto de valores de “x”, resolviendo
inecuaciones.
AUTOEVALUACIÓN

191. INGENIO
LAS INECUACIONES EN LA VIDA DIARIA
1. Situación problemática
Al igual que las ecuaciones, muchas de las situaciones que vivimos a diario pueden
traducirse en inecuaciones. Estas se encuentran presentes en diferentes tipos de
operaciones que realizamos. Por esta razón, es importante aprender a traducirlas y
resolverlas.
2. Finalidad
• Plantear problemas con inecuaciones y resolverlas.
• Comprender la utilidad de las inecuaciones y su presencia en nuestra vida cotidiana.
3. Recursos materiales
Periódicos, revistas. Papelotes.
Catálogos de productos. Tijeras.
Goma. Plumones.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
1.ª etapa 2.ª etapa
Organícense en grupos de 4
estudiantes.
Planteen un problema
de aplicación en la vida
cotidiana que sea resuelta con
inecuaciones.
Busquen en sus revistas o
periódicos las palabras y dibujos
que intervengan en su problema.
 Peguen sus recortes en un
papelote dándole la forma de un
problema.
Resuelven el problema,
identificando los datos, la
inecuación y la respuesta.
Los grupos sustentan el problema
resuelto en su papelote y lo
pegan en el interior del aula.
191
PROYECTO DE APRENDIZAJE N.0
8

192. Observa la imagen y contesta.
UNIDAD
1
Aprendemos a
Cultivamos valores
1
Reciclar es amar el planeta
• Responsabilidad.
• Educación para
la conciencia
ambiental.
•
Entender y conocer los elementos básicos
de la geometría.
• Reconocer la idea de punto.
•
Identificar las posiciones relativas de la recta.
•
Construir y representar rectas paralelas,
secantes y perpendiculares.
¿Cómo podemos contribuir a conservar nuestro medio ambiente?
¿Qué otros materiales podemos agrupar y reciclar?

193. INGENIO 193
Jugamos y aprendemos
Nos organizamos
PU NTOS
Y CUADRADOS
1. El primer jugador dibuja una línea en el lugar que
quiera, vertical u horizontalmente.
2.
El siguiente jugador, de igual modo, dibujará una
línea en el lugar que desee.
3.
Cada jugador podrá marcar una línea en donde
guste, tratando de formar más cuadrados antes
que el otro.
4.
El jugador que complete la última línea para
formar un cuadrado, gana ese cuadrado y
escribe la letra inicial de su nombre, tal como
muestra la imagen adjunta. (Fig. 2).
5.
Una vez que todos los puntos y las líneas han sido
completados, cuentan los cuadrados que han
marcado.
6. La persona que posee más cuadrados marcados
ganará el juego.
Fig. 1
M
M
M
V
V
Fig. 2
PU NTOS
Y CUADRADOS
1. Forma parejas de jugadores.
2. Dibuja en un hoja de papel un área cuadrada
o rectangular (ver Fig. 1) y llénala con puntos,
separados por la misma distancia, hasta que
el área este cubierta de cuadrados.
3. Lanza una moneda para decidir quién inicia
el juego.
LABORATORIO
1

194. INGENIO
4.° primaria
L U D O M A T I C
194 INGENIO
NOCIONES BÁSICAS
DE GEOMETRÍA
El punto
Se representa por la marca que deja la punta de un lápiz sobre el papel y se denota
con letra mayúscula.
A
Se lee Punto A.
• Línea:
En una sucesión indefinida de puntos, obtenemos líneas que pueden ser rectas,
curvas, quebradas y mixtas.
Gráficamente:
Línea recta Línea curva Línea mixta
Línea quebrada
TALLER
1
NOCIONES BÁSICAS DE GEOMETRÍA
Son los elementos
básicos de la
Geometría.
¿Qué sabemos
del punto, recta
y plano?
¿El horizonte del mar forma una línea recta o curva?
¿El sol nos da la idea de un punto?
Sí, puedo
ver líneas y
curvas.
¿Lucero
observas el
horizonte?

195. INGENIO
L U D O M A T I C
Geometría
195
La línea recta
Es la unión de infinitos puntos que siguen una misma dirección. No tiene origen ni fin.
La recta posee dos sentidos.
Gráficamente: se denota por dos letras mayúsculas o por una letra minúscula.
A B
,
Notación: ; se lee recta AB.
se lee recta ,.
, ; AB
 RAYO
Es una porción de recta limitada en un extremo e ilimitada en el otro.
 SEMIRRECTA
Es un rayo sin su origen.
Gráficamente:
O A
Notación:
OA ; OA.
se lee rayo
El plano
Es el conjunto de puntos ubicados en la trayectoria
descrita por el desplazamiento de una línea recta.
Lo más parecido a este elemento del espacio es una
hoja de papel, pero sin bordes; es decir, ilimitado y no
tiene grosor.
Gráficamente:
Notación:
P: plano P.
Importante
Importante
En la geometría;
los elementos
fundamentales
son: punto,
recta y plano.
Elpuntoeselelementobase
de la geometría, porque
con él determinamos las
rectas y los planos.
Sabías que ...
O B
origen sentido
OB : rayo OB
sentido
sentido
Sabías que ...

196. INGENIO
4.° primaria
L U D O M A T I C
196 INGENIO
ANALIZAMOS Y APRENDEMOS
Comunica el valor de verdad o
falsedaddelassiguientesproposiciones.
a) Se nombra los puntos con
letras mayúsculas. ( )
b) Por un punto pasan
infinitas rectas. ( )
c) Tres puntos forman un plano. ( )
d) Dos rectas secantes nunca
se cortan. ( )
Resolución:
a)
Es verdad (V). Se nombran todos los
puntos con letras mayúsculas.
b)
Es verdad (V). Por un punto pasan
infinitas rectas.
c)
Es falsa (F). Dado tres puntos,
colineales determina una recta.
d) Falso (F). Dos rectas secantes
siempre se cortan.
¿Cuántos segmentos de línea recta
encuentras en el siguiente gráfico?
Argumenta tu respuesta.
Resolución:
En total, observamos 8 segmentos de
línea recta:
a)
Observamos 2 segmentos de línea
recta en la parte superior.
b)
2 segmentos de línea recta en la
parte inferior.
c)
2 segmentos de línea recta en la
parte lateral derecha.
d)
2 segmentos de línea recta en la
parte lateral izquierda.
Identifica qué gráficos representan
la idea del plano. Argumenta tu
respuesta.
Resolución:
a) Elárbolnonosdauna
idea de plano.
b)
La bandera nos da
una idea de plano.
c)
La hoja nos da una
idea de plano.
Menciona y dibuja tres ideas de
plano.
Resolución:
a) La sábana nos da la
idea de plano.
b) La alfombra nos da
una idea de plano.
c) La toalla nos da una
idea de plano.
1 2
3 4

197. INGENIO
L U D O M A T I C
Geometría
197
PIENSO Y RESUELVO
AUTOEVALUACIÓN
INGENIO
Determina la cantidad de rectas que
pueden formarse con los siguientes
puntos.
Relaciona las siguientes columnas.
a) AB representa una Plano
recta.
b) A es un punto. AB
c) La superficie de una •A
hoja de papel.
Observa la figura y completa.
Puntos Rectas Planos
A
C
O
B D
P
Indicadores de evaluación
Reconozco los elementos básicos de la geometría.
Identifico un punto.
Identifico el plano.
Reconozco los diferentes tipos de líneas.
Relaciona cada gráfico con el
concepto respectivo.
I. Recta
II. Punto
III. Plano
1
3
2
4

198. INGENIO
198 INGENIO
Ubiquémonos en un plano
a) El plano pertenece a la Urb. Zárate.
b) El colegio está ubicado en la cuadra 11 de la Av. Gran Chimú.
c) Piero vive en la Av. Las Lomas.
Razonemos
a) ¿Qué camino debe de seguir Lucero para llegar al colegio?
b) Si viviera en la Av. Cajamarquilla, ¿cuál sería la ruta más corta para llegar a la Av. Las
Lomas?
c) Si Lucero viviera en la Av. Malecón Checa con Portada del Sol, ¿cuál sería la ruta
más corta para llegar al colegio?
d) ¿Qué tipo de rectas forman la Av. Gran Chimú y la Av. La Cantuta?
POSICIONES DE LA RECTA EN EL PLANO
Rectas paralelas
Dos rectas son paralelas cuando no coinciden en algún punto.
Gráficamente:
L1
L2
Notación: L1
// L2
La recta L1
es paralela a la recta L2
.
Las avenidas
La Cantuta y
Las Lomas no
se cruzan.
Piero
Lucero
COLEGIO
POSICIONES DE LA
RECTA EN EL PLANO
Yo vivo a dos
cuadras de
mi colegio.
¿Por qué algunas
rectas se cruzan
y otras no?
Porque las rectas
tienen diferentes
posiciones, como paralelas,
perpendiculares y secantes.
TALLER
2

199. INGENIO
L U D O M A T I C
Geometría
199
L1
3. Traza la recta.
L2
L1
L1
L2
L1
3. Haz coincidir uno de
losladosdelaescuadra
con la regla.
3. Traza una recta en
cualquier dirección.
Construcción para trazar rectas paralelas a una recta dada ( L ) haremos lo siguiente:
L2
L1
L1
a)
Traza una recta en
cualquier dirección con
la ayuda de una regla.
b)
Coloca la escuadra
por uno de sus
catetos apoyado
sobre la línea.
c)
Desplaza la escuadra
hacia el costado
derecho y traza la otra
línea paralela.
L1
Rectas secantes
Dos rectas son secantes, cuando se cortan en un punto.
Gráficamente:
L1
L2
O
Notación: L1
∩ L2
La recta L1
es secante a la
recta L2.
Rectas perpendiculares
Dos rectas son perpendiculares cuando forman un ángulo recto (90°).
Gráficamente:
Notación: L1
⊥ L2
La recta L1
es perpendicular
a la recta L2
.
L2
L1
Observación: para trazar rectas perpendiculares, haremos lo siguiente:

200. INGENIO
4.° primaria
L U D O M A T I C
200
ANALIZAMOS Y APRENDEMOS
1 2
3 4
¿ C u á l d e l o s s i g u i e n t e s
g r á f i c o s r e p r e s e n t a r e c t a s
perpendiculares?Argumenta tu
respuesta.
Resolución:
La base y el parante de la
lámpara nos representan
rectas perpendiculares,
pues ambas forman un
ángulo de 90°.
Los lápices forman rectas
secantes porque se cruzan
en un punto.
¿Cuál de los siguientes gráficos
representan rectas paralelas?
Argumenta tu respuesta.
Resolución:
a) Los lados laterales de las
escaleras representan
rectas paralelas porque
no se intersecan entre si.
b) Las agujas del reloj
representan dos rayos
que forman un ángulo.
c) Las rieles del tren,
representan rectas
paralelas, ya que no se
cruzan en algún punto.
Observa detenidamente qué tipo de
recta forma la calle B y C y qué recta
forma la Av. José María con la calle D.
Argumenta tu respuesta.
Av. José María
Calle
D
Calle
C
Calle
B
Av. Cruz del Sur
a) Calle B y calle C.
b) Av. José María y calle D.
Resolución:
Del siguiente croquis, identifica una calle
y una avenida que sean paralelas, asi
como otras que sean perpendiculares.
Av. Angamos
Av.
Callao
Av.
Las
aves
Av.
Las
aguilas
2do
extra
MERCADO
Av.
Rio
Calle Canevaro
Calle
Cerezas
casa de
materiales
ROCA
Av. Javier Prado
Resolución:
Hay varias soluciones, entre ellas:
Rectas perpendiculares
Rectas perpendiculares
Rectas paralelas
a) b)
Av. José María
Calle
D
calle
B
calle
C
Av. Javier Prado
Rectas paralelas
Av.
Las
Aguilas
Calle
Cerezas
a) b)
a) c)
b)
Av.
Las
Aves

201. INGENIO
L U D O M A T I C
Geometría
201
PIENSO Y RESUELVO
AUTOEVALUACIÓN
INGENIO
Observa detenidamente el plano
y contesta verdadero o falso,
argumentando tu respuesta.
a) Las calles Juan Belmonte y
Pepe Vásquez son paralelas. ( )
b) La calle Ignacio Sánchez y
Ortega forman rectas secantes. ( )
Del plano anterior de la pregunta 1,
completa los siguientes enunciados.
a)
Una calle perpendicular a Pascual
Márquez es…
b) Las calles Pascual Márquez y
Costillares forman rectas…
c) La calle Espartero es …
a la calle Gitanillo de Triana.
Coloca una regla sobre la hoja de tu
cuaderno y dibuja con un lápiz una
recta en cada una de los bordes.
¿Qué tipo de rectas representan las
gráficas?. Argumenta tu respuesta.
Representa gráficamente los tipos de
rectas que observas en los siguientes
objetos.
Indicadores de evaluación
Grafico rectas, paralelas, perpendiculares y secantes.
Reconozco rectas, paralelas, perpendiculares y secantes.
Resuelvo problemas con rectas, paralelas,
perpendiculares y secantes.
1
3
2
4

202. INGENIO
202
SIMETRÍA
EJE DE SIMETRÍA
Es una línea que divide a la figura en dos partes iguales.
Ejemplo:
Señala en cuál de los casos la línea determina una simetría.
a) b) c)
En los casos b y c, la línea determina simetría.
SIMETRÍA
Así es. Por lo
tanto, sus alas
son simétricas.
Dos figuras son
simétricas respecto a
un eje si, al doblarlas
por dicho eje, las
figuras coinciden.
¿Observas la
mariposa, Piero?
Sí, es hermosa
y sus dos alas
son iguales.
INGENIO
TALLER
3

203. INGENIO
L U D O M A T I C
Geometría
203
TRASLACIÓN
Es un movimiento en el plano para mover figuras, donde cada uno de sus puntos se
desplaza siguiendo una trayectoria.
Ejemplo:
Figura trasladada 11 cuadrados hacia la derecha y 2 cuadraditos hacia abajo.
Ejemplo:
Figura trasladada 2 cuadraditos hacia arriba y 10 cuadraditos hacia la derecha.
Piensa:
5
4
3
2
2
1
1
1
3
2
2
1
1
6 7 8 9 10 11
4 5 6 7 8 9 10
¿Qué letra es la simétrica de la letra P respecto
a la recta L1
?
¿Qué letra es la simétrica de la letra P respecto
a la recta L2
?
P
L1
L2

204. INGENIO
4.° primaria
L U D O M A T I C
204
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Completa la figura según el eje de
simetría.
Resolución:
a) Observamos la figura.
b) Graficamos la cantidad de
desplazamientos dados, teniendo
como referencia el eje de simetría.
Traza el eje de simetría de las siguientes
figuras.
Resolución:
Traslada la figura 12 cuadraditos a la
derecha y 2 cuadrados hacia abajo.
Resolución:
a)
Contamos12espaciosocuadraditos
hacia la derecha.
b)
Contamos 2 espacios hacia abajo.
c)
Graficamos partiendo de un punto
de referencia (A).
7
6
5
4
3
2
2
1
1
8 9 12
11
10
Traslada la siguiente figura 10
cuadraditos hacia la derecha y 8
cuadraditos hacia arriba.
Resolución:
a) b) c)
c) Grafiquemos la línea vertical,
de tal forma que divida al
gráfico en 2 partes iguales.
Grafiquemos la línea vertical,
de tal forma que divida al
gráfico en 2 partes iguales.
a)
Grafiquemoslalíneavertical,
de tal forma que divida al
gráfico en 2 partes iguales.
b)

205. INGENIO
L U D O M A T I C
Geometría
205
PIENSO Y RESUELVO
a)
c)
b)
d)
Traslada la figura 5 cuadraditos hacia
la derecha y 4 cuadraditos hacia
abajo.
Identifica y marca las figuras que sean
simétricas.
Traslada la figura 5 cuadraditos hacia
la derecha y 4 cuadraditos hacia
abajo.
Completa la figura simétrica.
Indicadores de evaluación
Aprendo el concepto de simetría y traslación.
Traslado los gráficos solicitados.
Completo la simetría de figuras.
1 2
4
3
AUTOEVALUACIÓN

206. LA IMPORTANCIA DE LAS LÍNEAS EN MIS DIBUJOS
PROYECTO DE APRENDIZAJE N.0
1
INGENIO
1. Situación problemática
El elemento más simple e importante con que contamos
para hacer un dibujo es la línea. Con ella, podemos realizar
dibujos y desarrollar obras de buena calidad, usándola de
diferentes formas y logrando efectos sorprendentes como
delimitar un espacio de otro y producir, mediante muchas
líneas, un efecto de degradado.
2. Finalidad
El alumno identifica los diferentes tipos de líneas y su importancia en la elaboración
de gráficos y/o dibujos.
3. Recursos materiales
Hojas bond. Goma, tijera.
Lápices. Borrador.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
INGENIO
1.ª etapa 2.ª etapa 3.ª etapa
Formen
grupos de 4
estudiantes.
Eligen un
tema a
dibujar. Por
ejemplo:
el mar, la
noche, mis
amigos, etc.
Recuerda que, al momento de dibujar
la mayoría de los dibujos, deben tener
líneas curvas y rectas.
Un dibujo con muchas de líneas rectas
y ángulos es más agresivo. Y es más
suave, amable e infantil un dibujo con
la mayor presencia de líneas curvas y
de cambios fluidos.
Presentan
y exponen
sus
trabajos.
206

207. UNIDAD
2
Observa la imagen y contesta.
Aprendemos a:
Cultivamos valores
¿Sabes lo que es estar prevenidos frente a un sismo?
¿En tu colegio hay zonas de seguridad en caso de sismo?
•
Educación para la
prevención.
•
Educación para la
gestión de riesgos.
•
Comprender la definición de un segmento
de recta.
•
Realizar operaciones de adición y
sustracción con segmentos de recta.
• Identificar el punto medio en el segmento.
Educación para la prevención

208. INGENIO
4.° primaria
L U D O M A T I C
208
LABORATORIO
2
Jugamos y aprendemos
Nos organizamos
TRES E N RAY A
1. Forma parejas de jugadores.
2. Dibuja en una hoja de papel un tablero de 9
cuadrados ver (Fig. 1).
3. Debes disponer de 4 chapas de color rojo y
4 de color azul ver (Fig. 2).
4. Lanza una moneda para decidir quién inicia
el juego.
1. El primer jugador coloca la ficha en uno de los
casilleros.
2.
El siguiente jugador, de igual forma, coloca la
ficha en uno de los casilleros.
3.
Un jugador gana si consigue tener una línea
de tres chapas de un mismo color.
4.
La línea formada por los jugadores puede ser
horizontal, vertical o diagonal.
5.
Gana el que forma primero la línea.
Fig. 1
Fig. 2

209. INGENIO 209
Gráficamente:
A B
A B
Notación:
Segmento AB: AB
Medida de un segmento
0 1 2 3 4 5 6 7 8 9 10 11 12 13
B
A
Del gráfico se observa que:
AB = 7 cm; se lee: “medida de AB es igual a 7 cm”.
SEGMENTO DE RECTA:
OPERACIONES
SEGMENTO
TALLER
4
A 7 metros de una
casa hay un faro, y
2 metros más cerca
hay una pelota.
¿A qué distancia
del faro se
encuentra la
pelota?
Un segmento es la porción de
recta limitada por dos puntos,
llamados extremos.
Las distancias se
pueden calcular se
mediante operaciones
con segmentos; pero
¿qué es un segmento?
Recuerda
Todo segmento tiene
una medida, la cual está
dada en unidades como
el milímetro, centímetro,
metro, etc.

210. INGENIO
4.° primaria
L U D O M A T I C
210
OPERACIONES CON SEGMENTOS
Adición de segmentos:
Ejemplo 1: Desdesucasaaltrabajo,Pierosedesplazaenautoyrecorreuna distanciade4km,
luego avanza 3 km más hacia su centro de estudios. ¿Qué distancia recorrió en
total?
Resolución:
Gráficamente:
4 km 3 km
A B C
Observamos que:
AC = AB + BC
Reemplazamos los datos:
AC = 4 km + 3 km
AC = 7 km
Respuesta: Piero recorrió una distancia de 7 km.
Sustracción de segmentos
Ejemplo 2:
Dados los puntos colineales y consecutivos A, B y C. Si el segmento AB mide
18 cm, el segmento AC mide 25 cm, ¿cuánto mide el segmento BC?
Resolución:
Gráficamente:
18 cm
25cm
A B C
Observamos que:
BC = AC – AB
Reemplazamos los datos:
BC = 25 cm – 18 cm
BC = 7 cm
Respuesta: el segmento BC mide 7 cm.
Recuerda
Semirrecta :
Rayos :
Segmentos:
PQ;
QP;
PQ;
QR
QR
QR
P
Las notaciones son muy
importantes
Q R

211. INGENIO
L U D O M A T I C
Geometría
211
ANALIZAMOS Y APRENDEMOS
Representa y comunica tu respuesta.
Johan maneja su auto y desde un punto
inicial avanza 7 m y luego retrocede
4 m. ¿A cuántos metros del punto inicial
se encuentra Johan?
Resolución:
a) Analizamos el problema.
Avanza = 7 m
Retrocede = 4 m
b) Representamos gráficamente.
c) Ejecutamos la estrategia.
MP = MN + NP
7 m = x + 4 m
7 m – 4 m = x
x = 3 m
d) Comunicamos la respuesta.
Johan se encuentra a 3 m del punto
inicial.
7 m
M N P
x 4 m
1 2 Piero camina 2 cuadras desde su casa
hacia la escuela localizada en la misma
línea recta. Al llegar, camina 3 cuadras
más para llegar a la librería. ¿Cuántas
cuadras caminó en total?
Elabora tu estrategia.
Resolución:
a) Comprendemos el problema.
Avanza1
= 2 cuadras
Avanza2
= 3 cuadras
b) Representamos gráficamente.
2 cuadras
Escuela Librería
3 cuadras
B
A C
c)Ejecutamos la estrategia.
AC = AB + BC
AC = 2 cuadras + 3 cuadras
AC = 5 cuadras
d) Comunicamos la respuesta.
Piero caminó en total 5 cuadras.
Sobre una recta, se ubican los puntos
consecutivos A, B, C, D. Si AB = 4 cm,
BC = 8 cm y AD = 34 cm. Calcula la
medida de CD. Interpreta y comunica
tu respuesta.
Resolución:
a) Interpretamos gráficamente.
A B C
34 cm
4 cm 8 cm x
D
b) Resolvemos:
AD = AB + BC + CD
34 cm = 4 cm + 8 cm + x
34 cm = 12 cm + x
34 cm – 12 cm = x
22 cm = x
c) Comunicamos la respuesta.
La medida del segmento CD es
22 cm.
3 4 Se tiene los puntos colineales y
consecutivos A; B; C y D. Si AB = 6 m,
BC = 2AB y CD = 2BC, calcula la longitud
de AD. Argumenta tu respuesta.
Resolución:
a)Interpretamos y graficamos:
B
A
6 m 12 m 24 m
C D
b) Resolvemos:
AD = AB + BC + CD
AD = 6 m + 12 m + 24 cm
AD = 42 m
c)
Argumentamos la respuesta.
El segmento AD es la suma de los
segmentos AB, BC y CD; por lo
tanto, su longitud es 42 m.

212. INGENIO
4.° primaria
L U D O M A T I C
212
AUTOEVALUACIÓN
4.° primaria
L U D O M A T I C
PIENSO Y RESUELVO
1 2
4
3
Indicadores de evaluación
Aprenda conceptualizar segmentos.
Interpreto y grafico segmentos.
Resuelvo problemas utilizando el concepto de
segmentos.
Paola camina en línea recta 10 m.
Luego, avanza 16 m y, finalmente,
camina 27 m. ¿ C u á n t o s m e t r o s
caminó en total? Grafica, interpreta
y comunica tu respuesta.
10 m
16 m
27 m
En una recta, se ubican los
puntos consecutivos A; B; C; y D,
de tal forma que AB = BC = 2CD.
Si CD = 24 m.¿Cuánto mide AB?
Argumenta tu respuesta.
Un atleta debe de correr 100 m,
siguiendo una línea recta. Si al
recorrer los primeros 40 m se agota
y se retira de la carrera, ¿cuántos
metros le faltó para llegar a la meta?
Grafica y argumenta tu respuesta.
40 m x
100 m
En la figura, calcula el valor de “x“.
A
(x + 21) cm (x + 8) cm
B C
49 cm

213. INGENIO
L U D O M A T I C
Geometría
213
PUNTO MEDIO
De nuestro ejemplo:
A B
M
4 m
2 m 2 m
Notación:
AM = MB; donde “M” es punto medio de AB.
SEGMENTOS II:
PUNTO MEDIO DE UN SEGMENTO
TALLER
5
Claro, eso permite
que el sube y baja
tenga equilibrio.
Observa que
el sube y
baja tiene un
punto medio.
¿Qué es el punto
medio de un
segmento?
Es el punto que divide
a un segmento en
dos partes iguales o
congruentes; es decir,
de igual longitud.
A
B
4 m
t.

214. INGENIO
4.° primaria
L U D O M A T I C
214
Ejemplo
Lucero se dirige del aula 1 al aula 2. Estas aulas están separadas por una distancia de
12 m y ella se encuentra en el punto medio de esta distancia. ¿Cuántos metros caminó?
Gráficamente:
12 m
A B
M
Salón 1 Salón 2
Resolución
a) Sabemos que:
AM = MB
b) Reemplazamos los datos.
AB = AM + MB
AB = AM + AM
AB = 2AM
12 m = 2 AM
AM = 6 m
c) Comunicamos la respuesta: Lucero recorrió 6 m.
Ejemplo 2
En el gráfico, M es punto medio del segmento AC. Calcula el valor de AC.
A C
M
3,5 m
3,5 m
Resolución
a) Sabemos que:
AM = MC (M: es punto medio)
b) Entonces:
AC = AM + MB
AC = 3,5 m + 3,5 m (AM = MC)
AC = 7 m
c) Comunicamos la respuesta:
El segmento AC mide 7 m.

215. INGENIO
L U D O M A T I C
Geometría
215
ANALIZAMOS Y APRENDEMOS
1 2
3 4
En el siguiente gráfico, C es punto medio
de BD. Calcula el valor de AC y argumenta
tu respuesta.
A B C
6 cm
6 cm
D
Resolución:
a) Sabemos que si “C” es punto medio, se
cumple que BC = CD = 6 cm.
b)Nos piden lo siguiente:
AC = AB + BC
AC = 6 cm + 6 cm
AC = 12 cm
c) El valor de AC es 12 cm.
Si P es punto medio del segmento AD,
calcula el valor de “x“. Comunica tu
respuesta.
A P
(x + 10) cm
(5x + 2) cm
D
Resolución:
a) Sabemos que si “P” es punto medio,
se cumple
AP = PD.
b) Reemplazamos los datos:
5x + 2 = x + 10
c) Resolvemos:
5x + 2 = x +10
5x – x = 10 – 2
4x = 8
x = 8/4
x = 2
d) Por lo tanto, el valor de x = 2.
En el gráfico, “B” es punto medio de AC.
Calcula el valor de “x”.
A B C
x + 8 cm 12 cm
Resolución:
a) Al ser B punto medio, se cumple que
AB = BC
b) Luego:
x + 8 = 12
x = 12 – 8
x = 4
c) El valor de “x” es 4.
Los puntos A, B, C y D están sobre una
recta, de modo que BC = 4 cm.
Si B es punto medio de AC y N punto
medio de CD; además, AD = 18 cm,
calcula el valor de ND.
Resolución:
a) Graficamos:
A B D
C N
18 cm
4 cm
b) Al ser B punto medio de AC se cumple
que: AB = BC; AB = 4 cm
c) Luego
AD = AC + CD
18 cm = 8 cm + CD
CD = 18 cm – 8 cm
CD = 10 cm
d) Al ser N punto medio de CD , CN = ND
e) El valor de ND es 5 cm.
CD = CN + ND
10 cm = ND + ND
10 cm = 2ND
ND = 5 cm
ND =
10 cm
2

216. INGENIO
4.° primaria
L U D O M A T I C
216
4.° primaria
L U D O M A T I C
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Aprendo el concepto de punto medio.
Interpreto y grafico segmentos.
Resuelvo problemas utilizando el concepto de
punto medio.
En el siguiente gráfico, la viga de
madera se corta por la mitad. Luego,
una de sus mitades se corta por
la mitad. Entonces, la viga queda
dividida en tres trozos, cuyas medidas
son:
8 m
En la siguiente figura, calcula la
medida del segmento BC, si C es el
punto medio del segmento BD.
A B D
C
16 cm
5 cm x
Dado los puntos consecutivos A,
B, y C. Calcular el valor de “x”.
Si AC = 48 cm y B es el punto medio
de AC.
A B C
2x + 2
En la figura, calcula la medida del
segmento PR si Q es punto medio.
P Q R
16 cm

217. INGENIO
L U D O M A T I C
Geometría
217
PLANO CARTESIANO
El plano cartesiano está formado por dos rectas numéricas: una vertical y la otra horizontal
que se cortan en un punto llamado origen.
Ejemplo:
Recta horizontal: llamada eje de las abscisas (x).
Recta vertical: Llamada eje de las ordenadas (y).
O: Origen
1
1
0 2
2
3
3
4
4
5
5
6
E
G
F
D
A
C
B
6
7
7
8
8
9
9
1
1
0
2
2
3
3
4
4
5
5
6
6
7
7
8
8
x
y
La flor se ubica en el par ordenado (2; 4).
El árbol se ubica en el par ordenado (6; 1).
PLANO CARTESIANO
TALLER
6
Entonces, el plano
cartesiano nos
sirve para ubicar
puntos.
¿Qué lindo
pececito?
¡Así es! El punto B
está formado por el
par ordenado (3: 7)
Lo hice ubicando
puntos en el plano
cartesiano.

218. INGENIO
4.° primaria
L U D O M A T I C
218
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Observa y determina, ¿qué figura se
ubica en (2; 1)?
1
1
2
3
4
5
6
7
8
2 3 4 5 6 7 8 9 10
0
Resolución:
a) La se ubica en el punto (3; 7).
b) La se ubica en el punto (1; 2).
c) La se ubica en el punto (2; 1).
d) La se ubica en el punto (4; 3).
Si un gráfico se ubica en el punto (2; 4)
y lo desplazamos 2 casilleros hacia
la derecha y 4 hacia abajo, ¿en qué
punto se encuentra?
1
1
2
3
4
5
6
7
8
2 3 4 5 6 7
2 D
8 9 10
0
Resolución:
La manzana se encuentra ubicado
finalmente en el punto (4; 0).
4 A
¿Qué gráfico se encuentra en el punto
(4; 2)? Argumenta tu respuesta.
Resolución:
En el punto (4; 2), está ubicado una
lavadora.
Completa los datos de la tabla. Traslada
la figura a los puntos (x + 4; y + 2)
1
1
2
3
4
5
6
y
C
A
B
2 3 4 5 6 7 8 9 10 x
0
Resolución:
Observamos que:
•
El punto A está formado por el par
ordenado (1; 2); entonces, traslado 4
posiciones en x y 2 posiciones en y. Así,
tendremos el nuevo par ordenado (5; 4).
•
El punto B está formado por el par
ordenado (1; 6); entonces, traslada 4
posiciones en x y 2 posiciones en y. Asi,
tendremos el nuevo par ordenado (5; 8).
•
El punto C está formando por el par
ordenado (5; 6); entonces, traslada 4
posiciones en x y 2 posiciones en y. Así,
tendremos el nuevo par ordenado (9; 8).
Graficamos:
1
1
2
3
4
5
6
7
8
y
C
A
B
2 3 4 5 6 7 8 9 10 x
0
1
1
2
3
4
5
6
7
8
y
2 3 4 5 6 7 8 9 10 x
0

219. INGENIO
L U D O M A T I C
Geometría
219
INGENIO
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Reconozco el plano cartesiano.
Interpreto la ubicación de figuras en el plano
cartesiano.
Represento figuras en el plano cartesiano.
En qué punto está ubicado la pelota.
Argumenta tu respuesta.
1
1
2
3
4
5
y
2 3 4 5 6 7 8 x
0
Determina el valor de verdad de las
siguientes proposiciones.
a)
Al eje “x” se le llama también eje
de las ordenadas. ( )
b)
El par ordenado es un punto ( )
en el plano cartesiano.
c)
El plano cartesiano está ( )
formado por 2 rectas
perpendiculares.
Observa y realiza lo siguiente:
a)
Pinta de azul el eje de las abscisas.
b) Pinta de rojo el eje de las ordenadas.
c)
Anota el punto donde se ubica la
muñeca.
y
x
1
1
2
3
4
5
6
7
8
2 3 4 5 6 7 8 9 10
0
Desplaza un objeto ubicado en el
punto (4; 3) hacia el punto (x + 2; y – 1).
Comunica su nueva ubicación.
y
x
1
1
2
3
4
5
6
7
2 3 4 5 6 7
0

220. USO DE LOS SEGMENTOS
PROYECTO DE APRENDIZAJE N.0
2
1. Situación problemática
Muchas situaciones de la vida diaria como el crecimiento de la población, el consumo
del agua, de la luz, etc., puede ser representadas gráficamente a través de segmentos.
Estas representaciones nos servirán visualmente para el análisis y comprensión de un
hecho.
2. Finalidad
Que el alumno interprete y elabore gráficas formadas por segmentos de recta que
modelan situaciones relacionadas con la vida diaria.
3. Recursos materiales
Hojas bond. Goma, tijera. Lápices. Borrador.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
5. Evaluación
INGENIO
1.ª etapa 2.ª etapa 3.ª etapa
Forman
grupos
de 4
estudiantes.
Eligen un
tema. Por
ejemplo: la
asistencia
de los
alumnos y
alumnas
del aula
durante los
cinco días.
Presentan los datos en un cuadro.
Ejemplo:
23
Lunes
Martes
Miércoles
Jueves
Viernes
Nº de alumnos
Días
Grafica la información.
Nº de
alumnos
Días
Lunes Martes Miércoles
5
10
15
20
100%
0%
Interpreta la información recolectada.
Presentan
y
exponen
sus
trabajos.
220

221. Observa la imagen y contesta.
UNIDAD
3
Aprendemos a
Cultivamos valores
Educación para la paz
¿Qué entiendes por vivir en paz?
¿Cómo crees tú que podemos vivir en un mundo de paz y armonia?
•
Educación para la
paz.
•
Tolerancia.
• Definir y representar a los ángulos.
•
Representar la medida de los ángulos.
• Graficar y medir los ángulos.

222. INGENIO
4.° primaria
L U D O M A T I C
222
Jugamos y aprendemos
Nos organizamos
CONSTRU YO EL
TRANSPORTADOR
Debes disponer de:
• Cartulina gruesa.
• Lápices.
• Tijera.
1. Coloca un vaso sobre la cartulina.
Observa la figura.
2. Pasa el lápiz sobre el contorno del vaso y
recorta la figura marcada.
3. Dobla la figura por la mitad y recorta.
4. Dobla la figura recortada.
5. Escribe, en cada espacio formado por la
doblez, 10 grados, 20 grado, etc.
6. Ahora, ya puedes empezar a medir ángulos.
10°
20°
30°
40°
50°
60°
70°
80°
90°
LABORATORIO
3

223. INGENIO
L U D O M A T I C
Geometría
223
Elementos de un ángulo
OA y OB : lados del ángulo
O: vértice
Notación: AOB, BAOB, O
Se lee ángulo AOB
¿Cómo medir un ángulo?
a) Observa el ángulo que forman las hojas de la tijera.
ÁNGULOS
MEDICIÓN DE ÁNGULOS
TALLER
7
Sí, su esquema se
forma por rayos
que tienen puntos
en común.
Observa la
casa, Lucerito.
¿ Qué es un
ángulo?
Es aquel que está
formado por dos rayos
y tienen un punto en
común.
O
A
B

224. INGENIO
4.° primaria
L U D O M A T I C
224
b) Graficamos:
O
B
A
c) Para medir el valor del ángulo, usamos el transportador, el cual es un semicírculo
graduado. Hacemos coincidir el centro del transportador con el vértice del ángulo
y su lado inicial.
A
B
O
45°
d) La medida de los ángulos se lee en sentido opuesto a las manecillas del reloj.
e) Comunicamos la medida: el ángulo mide 45 grados sexagecimales.
Ejemplo:
Usa el transportador para medir los siguientes ángulos
O A
B
mAOB = 130°
∧
N
M
O
mMON = 25°
∧
O M
N
55°
mMON = 55°
∧ P
Q
O
mPOQ = 90°
∧

225. INGENIO
L U D O M A T I C
Geometría
225
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Representa el ángulo y efectúa la
medición. Comunica tu resultado.
Resolución:
a) Representamos
b) Realizamos la medición, haciendo
uso de un transportador.
36°
c) Comunicamos la respuesta.
E l á n g u l o m i d e 3 6 g r a d o s
sexagecimales.
Mide el siguiente ángulo.
A
B
O
Resolución:
a) Colocamos el transportador,
haciendo coincidir el vértice del
á n g u l o c o n e l c e n t r o d e l
transportador.
b) Comunicamos la respuesta.
El ángulo mide 90°.
Grafica un ángulo de 140ª.
Resolución:
a. Dibujamos un rayo.
b.
Hacemos coincidir el centro del
transportador con el punto O del
rayo y hacemos una marca en la
ubicación de 140° que indica el
transportador.
140°
c.
Trazamos el otro lado del ángulo para
lo cual nos ayudamos de una regla.
A
B
0
d. Simbolizamos nuestra respuesta.
m AOB = 140°
¿
Cuánto mide el ángulo formado por
las manecillas del reloj?
Resolución:
a)Representamos
gráficamente.
b) Colocamos el
transportador,
haciendo coincidir
el vértice del
ángulo con el centro
del transportador.
c) C o m u n i c a m o s l a
112°
respuesta.
El ángulo mide 112°.
A
B
0
90°

226. INGENIO
4.° primaria
L U D O M A T I C
226
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Aprendo identificar los elementos de un ángulo.
Grafico la medida del ángulo solicitado.
Represento correctamente a un ángulo.
Representa y mide el ángulo formado
por los dedos índice y medio.
Comunica la medida del siguiente
ángulo.
En la figura, calcula la medida del
ángulo AOC.
A
C
O
Identifica los elementos del ángulo
QOP.
Q
P
O

227. INGENIO
L U D O M A T I C
Geometría
227
CLASIFICACIÓN DE ÁNGULOS
Ángulo agudo
Es aquel ángulo cuya medida es mayor que 0° y menor que 90°.
Gráficamente:
O
A
B
0° mAOB 90°
¿ Las manecillas
del reloj forman
diferentes tipos
de ángulos?
¿ Cuánto medirá
cada uno de
ellos?
CLASIFICACIÓN DE
ÁNGULOS
TALLER
8
¿De acuerdo a sus
medidas, cómo
podemos clasificar
los ángulos?
Los ángulos se
clasifican en agudos,
rectos y obtusos.

228. INGENIO
4.° primaria
L U D O M A T I C
228
Ángulo recto
Es aquel ángulo cuya medida es igual a 90°.
Gráficamente:
A
O
B
mAOB = 90º
Ángulo obtuso
Es aquel ángulo cuya medida es mayor que 90º y menor que 180º.
Gráficamente:
A
O
B
90º mAOB 180º
B A
180º
mAOB = 180º
Ángulo llano
Es aquel ángulo cuya medida es igual a 180º.
Gráficamente:

229. INGENIO
L U D O M A T I C
Geometría
229
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Representa cuatro ángulos agudos.
Resolución:
a)Observamos:
b)Representamos:
Representa tres ángulos rectos.
Resolución:
a)Observamos:
b)Representamos:
¿Qué tipo de ángulo forman los dedos
abiertos? Argumenta la respuesta.
Resolución:
a)Observamos:
b)Representamos:
c)
Los dedos forman un ángulo agudo,
pues la medida de su abertura es
menor de 90°.
Grafica un ángulo agudo, un ángulo
recto y un ángulo obtuso.
Resolución:
a) Graficamos un ángulo agudo.
Sabemos que su medida es menor
a 90°.
50°
b)Graficamos un ángulo recto.
Sabemos que su medida es igual a
90°.
c) Graficamos un ángulo obtuso.
Sabemos que su medida es mayor
a 90°.
120°

230. INGENIO
4.° primaria
L U D O M A T I C
230
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Aprendo a clasificar los diferentes tipos de ángulo.
Grafico los diferentes tipos de ángulo.
Resuelvo problemas usando el concepto de
clasificación de ángulos.
Grafica 2 ángulos agudos, 2 ángulos
obtusos y 1 ángulo recto en diferentes
posiciones.
En el siguiente gráfico, ¿cuánto mide
el ángulo AÔC y qué tipo de ángulo
forma?
D
C
B
O
A
10°
20°
30°
Observa y escribe la cantidad de
ángulos rectos que hay en el gráfico.
Ubica y grafica los ángulos agudos,
obtusos y rectos que presenta la
imagen.

231. 1. Situación problemática
Las matemáticas tienen una gran aplicación directa en la arquitectura. Antes
de la obra, el arquitecto tiene que comprobar que la estructura que quiere
construir es realizable, teniendo en cuenta la resistencia de los materiales que empleará,
las cargas que tienen que soportar, etc. En nuestro Perú incaico, exactamente en
Cusco, sobresale una de las maravillosas construcciones, conocida como la «piedra de
12 ángulos», de la cual se dice, sería la piedra llave del muro; es decir, si se la saca, se
caería gran parte del muro.
2. Finalidad
El alumno reconoce la importancia de los ángulos como elementos en las construcciones
y edificaciones.
3. Recursos materiales
Hojas bond. Goma, tijera. Lápices. Borrador.
4. Etapas y actividades
ÁNGULOS
PROYECTO DE APRENDIZAJE N.0
3
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
INGENIO
1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de 4
estudiantes.
Investigan la historia
de la «piedra de los 12
ángulos» ubicada en la
calle Hatun Rumiyoc de
la ciudad del Cusco.

Elaboran un resumen
de la historia de la
«piedra de los 12
ángulos».
Elaboran una
maqueta con arcilla
que represente a
la «piedra de los 12
ángulos».
Presentan y
expone el
material a la
clase.
Argumentan
la importancia
de la «piedra
de los 12
ángulos».
231

232. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
232
Observa la imagen y contesta.
UNIDAD
4
Aprendemos a
Cultivamos valores
¿Cómo es la convivencia en tu escuela?
¿Consideras que la convivencia es importante en tu escuela? ¿Por qué?
• Educación para la
convivencia, la
paz y la ciudadanía.
• Representar y definir la clasificación
de los ángulos.
• Identificar, interpretar y resolver
operaciones con ángulos.
• Aplicar las propiedades para la
resolución de problemas.
Convivir en igualdad y respeto

233. L U D O M A T I C
Geometría
INGENIO
INGENIO 233
Geometría
Jugamos y aprendemos
Nos organizamos
SUMAMOS Y
RESTAMOS ÁNGULOS
LABORATORIO
4
60° 50°
20°
10°
30°
40°
10° 20°
50°
60°
30° 40°
Fig. 2
+ = 50°
10°
– 20°
=
Forman grupos de dos personas y preparan los
siguientes materiales:
1. Un tablero. Fig. 1.
2. Dos dados con las características de la Fig. 2.
1. Uno de los jugadores iniciará el juego.
2. Si al tirar los dados, las caras que quedan
arriba son del mismo color, tendrás que sumar
los dos números que hayan aparecido. El
número de casillas que avanzarás será el
resultado de la suma.
3. Si al tirar los dados, las caras que quedan
arriba son de distinto color, tendrás que restar
los dos números, siempre el mayor menos el
menor. El número de casillas que avanzarás
será el resultado de la resta.
4. Gana el juego el primero en llegar a la meta.
Fig. 1

234. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
234
CLASIFICACIÓN DE LOS ÁNGULOS
DE ACUERDO A LA POSICIÓN DE LOS LADOS
Ángulos consecutivos
Dos o más ángulos son consecutivos cuando tienen el mismo vértice y están uno a
continuación del otro.
Gráficamente:
O
C
D
B
A
Son ángulos consecutivos AOB, BOC y COD
ÁNGULOS II:
CLASIFICACIÓN DE LOS ÁNGULOS
TALLER
9
Miren las líneas de esta
concha, son consecutivas
y algunas se reflejan en
sentido opuesto.
Los ángulos
tienen diferentes
medidas, ¿pueden
clasificarse?
Por supuesto, se
clasifican según:
a. La posición de sus lados.
b.
De acuerdo a la suma
de sus medidas.

235. L U D O M A T I C
Geometría
INGENIO
INGENIO 235
Ángulos opuestos por el vértice
Son dos ángulos que tienen un vértice en común y sus lados son rayos opuestas. Los
ángulos opuestos por el vértice tienen igual medida.
Gráficamente:
A C
B D
DE ACUERDO A LA SUMA DE SUS MEDIDAS
Ángulos complementarios
Dos ángulos son complementarios cuando la suma de sus medidas es igual a 90°.
Gráficamente:
A
B
C
O
Ángulos suplementarios
Dos ángulos son suplementarios cuando la suma de sus medidas es igual a 180°.
Gráficamente:
A
B
C
0
Caso especial
Tres o más ángulos consecutivos suman 360ª.
Gráficamente:
O
A B
C
aº aº
a + b = 90º
φ + w = 180º
a + b + γ = 360º
bº
aº
φº
wº
γº bº
aº

236. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
236
ANALIZAMOS Y APRENDEMOS
1 2
3 4
Representa gráficamente y argumenta
qué tipo de ángulo forman una de las
alas de la mariposa.
Resolución:
a) Observamos
b)
Representamos gráficamente:
c) Tenemos dos ángulos consecutivos,
pues tienen un lado en común.
Representa gráficamente y argumenta
qué tipo de ángulo forman las alas y
la cola del cóndor.
Resolución:
a) Observamos:
b) Representamos gráficamente:
c) Argumentamos la respuesta.
Tenemostresángulosconsecutivos,
y la suma de ellos es 180º.
Representa gráficamente y argumenta
qué tipo de ángulo forman los brazos
del molino.
Resolución:
a)
Observamos y representamos
gráficamente.
b) Argumentamos la respuesta:
Tenemos ángulos opuestos por el
vértice.
Representagráficamenteyargumenta
qué tipo de ángulo forman las alas de
la mariposa.
Resolución:
a)Representamos gráficamente.
b)
Tenemos ángulos opuestos por el
vértice y estos tienen igual medida.

237. L U D O M A T I C
Geometría
INGENIO
INGENIO 237
PIENSO Y RESUELVO
AUTOEVALUACIÓN
1 2
4
3
Indicadores de evaluación
Aprendo identificar los elementos de un ángulo.
Grafico la medida del ángulo solicitado.
Denoto correctamente a un ángulo.
Traza los diferentes ángulos que
observas y clasifícalos de acuerdo a
su medida.
¿Qué tipo de ángulos están formando
las manecillas del reloj. Argumenta tu
respuesta.
¿Qué ángulos forman las hojas y
el mango de la tijera? Representa
gráficamente y argumenta tu
respuesta.
Representa gráficamente los ángulos
que forman las porciones de la pizza
y argumenta qué tipo de ángulos
forman.

238. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
238
Ejemplos:
1. En la figura, calcula la medida del ángulo AOC.
75°
48°
A
O
C
B
Solución:
Por adición de sus ángulos
a) mBAOC = mBAOB + mBBOC
b) mBAOC = 75° + 48°
c) mBAOC = 123°
Respuesta: El ángulo AOC mide 123°.
Av. Miraflores Av. Shell
48°
42°
Av. Conquistadores
Av.
Larco
OPERACIONES CON ÁNGULOS
OPERACIONES
CON ÁNGULOS
TALLER
10
¿Cuánto mide el
ángulo que forma
la Av. Larco y la
Av. Shell?
¿Qué operaciones
se puede realizar
con los ángulos?
Se puede realizar
la adición y
sustracción de
ángulos.
Bastará trabajar con la
medida de los ángulos
que se observan en el
gráfico.

239. L U D O M A T I C
Geometría
INGENIO
INGENIO 239
Recuerda
2. Calcula el valor de φ.
A
C
B
O
52°
φ
Resolución:
a) El ángulo AOC mide 90°.
b) Por sustracción de ángulos
φ = 90° – 52°
φ = 38°
Respuesta: El ángulo BOC mide 38°.
3. Calcula el valor del ángulo MOP.
84°
42°
N
P
M
O
Resolución:
a) mMOP = 42° + 84°
mMOP = 126°
b) El ángulo MOP mide 126°.
4. Calcular el valor de x.
Resolución:
a) Los ángulos AOB y COD son
opuestos por el vértice.
mBCOD = mBAOB
b) Entonces: x = 34°.
Respuesta: El ángulo COD mide 34º.
Según su medida un ángulo
puede ser
• Agudo: mide más de 0º y
menos de 90º.
• Recto: mide 90º.
• Obtuso: mide más de 90º
y menos de 180º
• Llano: mide 180º.
B
A O B
O B
A
O B
A
A
O
A
B
34º
C
D
xº
O

240. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
240
Determina el valor del ángulo x.
24°
56°
x
A
O
C
B
Resolución:
a) Observamos.
El ángulo AOB y el ángulo BOC
son ángulos consecutivos.
b) Por lo tanto:
x + 24° = 56°
x = 56°-24°
x = 32°
c) Comunicamos la respuesta.
El ángulo AOB mide 32°.
Calcula el valor de “n“ y comunica tu
respuesta.
20°
n
46°
Resolución:
a) Observamos el gráfico: “n “es la
suma de 20° y 46°.
b) Por lo tanto:
n = 20º + 46°
n = 66°
c)
Comunicamos la respuesta.
El valor de n es 66°.
En la gráfica siguiente, calcula el
valor de b? Argumenta tu respuesta.
b
56°
Resolución:
a) Observamos que son ángulos opues-
tos por el vértice.
b) Por lo tanto:
b = 56°
c) Argumentamos la respuesta.
El valor de b es 56°.
En el siguiente gráfico, calcula el
valor del ángulo w. Comunica tu
respuesta.
A
B
O
w
62°
Resolución
a) Observamos, que la m B AOB es 90°.
b) Por lo tanto:
62 + w = 90°
w = 90° – 62°
w = 28°
c)
Comunicamos la respuesta.
El valor de w es 28°.
1 2
4
3
ANALIZAMOS Y APRENDEMOS

241. L U D O M A T I C
Geometría
INGENIO
INGENIO 241
Grafica y resuelve. Si un ángulo mide
35º y su consecutivo mide el doble,
¿cuánto sumarán ambos ángulos?
x
35°
En el siguiente gráfico, determina el
valor del ángulo x.
x
23°
En el siguiente gráfico, calcula el
valor de b.
b
95°
43°
En el siguiente gráfico, calcula el valor
del ángulo AOD.
D
A
C
B
33° 38°
38°
O
C
C
A
B
C
O
O A
B
• •
B
A
D
1
PIENSO Y RESUELVO
3
2
4
AUTOEVALUACIÓN
Indicadores de evaluación
Aprendo a identificar los elementos de un ángulo.
Grafico la medida del ángulo solicitado.
Denoto correctamente a un ángulo.

242. 1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de
4 estudiantes.
Investigan
y resuelven
diferentes
situaciones de
la vida diaria en
donde se utilice
el concepto y
operaciones con
ángulos.
Conversan sobre situaciones cotidianas,
y plantean ejemplos como:
• ¿ Q u é á n g u l o
forman las piernas
de la gimnasta?
• ¿Cuánto debe de
medir el ángulo
que recorrerá el
árbol para que se
encuentre en una
posición recta?
Presentan
y exponen
sus
trabajos.
PROYECTO DE APRENDIZAJE N.0
4
INGENIO
1. Situación problemática
Los ángulos son parte de nuestra vida cotidiana; por ejemplo, cuando en casa quieres
colocar un cuadro debes ponerlo a un ángulo de 90 grados con respecto a la pared. Los
techos de las casas tienen cierto ángulo de inclinación para que el agua de la lluvia
resbaleynoquedeestancadaenlostechos,evitandolasgoteras,etc.Ennuestravidadiaria,
hay muchas cosas que puedes ver a tu alrededor, observando que es importante colocar
ciertos ángulos.
2. Finalidad
El estudiante aplicará y reconocerá en la vida diaria los diferentes usos de los ángulos.
3. Recursos materiales
Hojas bond. Goma, tijera. Lápices. Borrador.
4. Etapas y actividades
Tiempo
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones
asignadas.
ÁNGULOS II
242

243. TRIÁNGULOS
Educación en derechos humanos
Cultivamos valores
•
Educación para los
derechoshumanos.
•
Respeto.
Aprendemos a
•
Reconocer los triángulos en nuestro
entorno y su importancia.
•
Definir y clasificar los triángulos
.
Observa la imagen y contesta.
¿Sabes qué es la Declaración Universal de los Derechos Humanos?
¿Conoces cuáles son tus derechos?
UNIDAD
5

244. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
244
ARMA
TRIÁNGULOS
Nos organizamos
1. Forma parejas de jugadores.
2. Debes disponer de 6 a 8 palitos de madera
o plástico. (Ver fig. 1).
Jugamos y aprendemos
1. Forma con tres palitos un triángulo. (Ver fig. 2).
2. Ahora, forma dos triángulos con cinco palitos.
3. Finalmente, con seis palitos forma
cuatro triángulos.
Gana el juego la pareja
que logra formar los
triángulos solicitados en el
menor tiempo.
5
LABORATORIO
(Fig. 1)
(Fig. 2)

245. L U D O M A T I C
Geometría
INGENIO
INGENIO 245
TRIÁNGULOS I
ELEMENTOS
Lados : AB, BC, AC
a
C
B
A
b
q
Vértices : A, B, C
Ángulos Interiores : a, b, q
CONCEPTO DE TRIÁNGULO
11
TALLER
Tiene 3 lados.
¡Oh!, Miguel, mira
la figura que hemos
formado. Es un triángulo.
¿Qué es un triángulo?
Es la figura geométrica que
resulta de unir tres puntos
no colineales mediante
segmentos de recta.

246. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
246
Triángulo isósceles
Es aquel triángulo que presenta dos lados de igual longitud y uno desigual.
Gráficamente:
A
B C
A
B C
Se cumple
AB = AC AB ≠ BC AC ≠ BC
Triángulo equilátero
Es aquel triángulo que presenta los tres lados de igual longitud.
Gráficamente:
A
B C A
B C
Se cumple
AB = BC = AC
Triángulo escaleno
Es aquel triángulo que presenta los tres lados de diferente longitud.
Gráficamente:
A
B
C A
B C
Se cumple
AB ≠ BC ≠ AC
CLASIFICACIÓN DE LOS TRIÁNGULOS
De acuerdo a la longitud de sus lados:

247. L U D O M A T I C
Geometría
INGENIO
INGENIO 247
En el siguiente gráfico, determina el
tipo de triángulo que representa la
parte sombreada.
Comunica tu respuesta.
6 cm
6 cm
6 cm
Resolución:
Eltriángulorepresentadoesequilátero,
pues sus 3 lados tienen igual medida
(6 cm).
En el siguiente gráfico, determina el
tipo de triángulo que representa la
parte sombreada.
Comunica tu respuesta.
6 cm
6 cm
6 cm
Resolución:
Eltriángulorepresentadoesequilátero,
pues sus 3 lados tienen igual medida
(6 cm).
¿Qué tipo de triángulo forman los
aleros de la casa? Argumenta tu
respuesta.
Resolución:
Los aleros de la casa forman un
triángulo isósceles, pues tiene forma
triangular y dos de sus lados tienen
igual medida.
¿Qué tipo de triángulo forman los
aleros de la casa? Argumenta tu
respuesta.
Resolución:
Los aleros de la casa forman un
triángulo isósceles, pues tiene forma
triangular y dos de sus lados tienen
igual medida.
¿Qué tipo de triángulo representa
el siguiente instrumento musical?
Argumenta tu respuesta.
Resolución:
Se observa un triángulo isósceles,
pues dos de sus lados tienen igual
medida.
¿Qué tipo de triángulo representa
el siguiente instrumento musical?
Argumenta tu respuesta.
Resolución:
Se observa un triángulo isósceles,
pues dos de sus lados tienen igual
medida.
ANALIZAMOS Y APRENDEMOS
1
3
2
Ubica en la tabla cada uno de los
siguientes triángulos.
Resolución:
Ubica en la tabla cada uno de los
siguientes triángulos.
Resolución:
4
Triángulo Escaleno Isósceles Equilátero
X
X
X
X
X

248. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
248
(x + 4) cm
A
B
C
10 cm
1
PIENSO Y RESUELVO
3
2
4
10 m
C
8 m
Piero
Rosa Johan
AUTOEVALUACIÓN
Indicadores de evaluación
Aprendo a clasificar triángulos de acuerdo a la
medida de sus lados.
Represento gráficamente los diferentes tipos de
triángulos.
Resuelvo problemas que implican el uso de triángulos.

249. L U D O M A T I C
Geometría
INGENIO
INGENIO 249
Triángulo rectángulo
Es aquel triángulo que tiene un ángulo que mide 90º.
Gráficamente:
m B ABC = 90º
TRIÁNGULOS II
DE ACUERDO A LA MEDIDA DE SUS ÁNGULOS
B C
A
¡Oh! ¡Cuántos
triángulos!
Observo un
triángulo que tiene
un ángulo recto.
¿De qué otra forma
podemos clasificar
los triángulos?
De acuerdo a la medida de
sus lados, los clasificamos en…
• Triángulo rectángulo.
• Triángulo acutángulo.
• Triángulo obtusángulo.
TALLER
12

250. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
250
Triángulo acutángulo
Es aquel triángulo cuya medida de sus ángulos internos es menor a 90º.
Gráficamente
B C
A
mBABC 90º, mBACB 90º, mBBAC 90º
Triángulo obtusángulo
Es aquel triángulo que tiene un ángulo interior cuya medida es mayor a 90º, pero menor
que 180º.
Gráficamente:
B
C
A
90º mBABC 180º
Teorema fundamental de todo triángulo
La suma de las medidas de los ángulos internos de un triángulo es 180º.
B C
A
b c
a
a + b + c = 180º

251. L U D O M A T I C
Geometría
INGENIO
INGENIO 251
Determina el valor de verdad o
falsedad de las siguientes
proposiciones:
a) Todo triángulo rectángulo
tiene un ángulo recto. ( )
b) No es cierto que el
triángulo obtusángulo
tiene un ángulo mayor a 90º. ( )
c) Si un triángulo es
acutángulo, entonces sus
ángulos tienen medidas
menores a 90º. ( )
Resolución:
a) Es verdad.
b) Falso, todo triángulo obtusángulo
tiene un ángulo mayor a 90º.
c) Es verdad.
Determina el valor de verdad o
falsedad de las siguientes
proposiciones:
a) Todo triángulo rectángulo
tiene un ángulo recto. ( )
b) No es cierto que el
triángulo obtusángulo
tiene un ángulo mayor a 90º. ( )
c) Si un triángulo es
acutángulo, entonces sus
ángulos tienen medidas
menores a 90º. ( )
Resolución:
a) Es verdad.
b) Falso, todo triángulo obtusángulo
tiene un ángulo mayor a 90º.
c) Es verdad.
En el siguiente triángulo, determina el
valor de “x”.
B
C
A
Resolución:
a) 108º + x = 180º
x = 72º
b)
En el siguiente triángulo, determina el
valor de “x”.
B
C
A
Resolución:
a) 108º + x = 180º
x = 72º
b)
Lucero pasea a su perro por las
calles indicadas. ¿Qué triángulo
forma su recorrido?
Resolución:
Lucero inicia su recorrido en el
punto P.
Al terminar la primera calle (punto
Q) gira hacia la izquierda,
formando un ángulo de 90º.
c) Luego, gira para regresar al punto
inicial, formando un triángulo
rectángulo.
Lucero pasea a su perro por las
calles indicadas. ¿Qué triángulo
forma su recorrido?
Resolución:
Lucero inicia su recorrido en el
punto P.
Al terminar la primera calle (punto
Q) gira hacia la izquierda,
formando un ángulo de 90º.
c) Luego, gira para regresar al punto
inicial, formando un triángulo
rectángulo.
Q
P
R
ANALIZAMOS Y APRENDEMOS
Acutángulo Rectángulo Obtusángulo
X
X
X
X
X
X
1
2
3
4
5
6
6
3
2
5
1
4
#
Mide los ángulos de los siguientes
triángulos y completa la tabla.
Resolución:
a) Usamosuntransportadorparamedir
los ángulos de cada triángulo.
b) Ubicamos cada triángulo en la
tabla que le corresponde.
1
4
3
2

252. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
252
AUTOEVALUACIÓN
PIENSO Y RESUELVO
1 2
3 4
Indicadores de evaluación
Aprendo a clasificar los triángulos de acuerdo a la
medida de sus ángulos.
Represento gráficamente los diferentes tipos de
ángulos de acuerdo a su medida.
Resuelvo problemas que implican el uso de trián-
gulos de acuerdo a su medida.

253. 253
INGENIO
1. Situación problemática
Las estructuras triangulares difícilmente se deforman cuando actúan sobre ellas fuerzas
físicas, añadiendo estabilidad y soporte a otras estructuras. Por eso, muchos puentes,
edificios, juegos mecánicos, etc. tienen a los triángulos como agentes estabilizadores.
2. Finalidad
El alumno recrea la importancia de los triángulos en la estabilidad de las estructuras de
nuestro entorno.
3. Recursos materiales
Cartulina. Lápices. Borrador.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
PROYECTO DE APRENDIZAJE N.0
5
TRIÁNGULOS
1.ª etapa 2.ª etapa 3.ª etapa
Forman
grupos
de 4
estudiantes.
Forman dos columnas utilizando libros
y colocan una hoja de cartulina sobre
éstos. Luego, encima de la cartulina
ponen un cuaderno. ¿Qué sucede?
Doblan sucesivamente la cartulina y la
colocan como se muestra en la figura.
Pon de nuevo el libro encima de la
cartulina ¿Qué sucede ahora?
Anota todas las observaciones.
Comparan,
discuten y
consolidan
los
resultados
obtenidos.

254. UNIDAD
Educación en valores
Cultivamos Valores
• Educación
en Valores y
formación ética.
• Tolerancia.
Aprendemos a:
•
Reconocer y definir los elementos del
cuadrilátero.
• Aplicar y argumentar las propiedades
de los problemas.
Observa la imagen y contesta.
¿Qué valores prácticas en casa y en el colegio?
¿Por qué son importantes los valores en nuestra convivencia diaria?
6 CUADRILÁTEROS

255. L U D O M A T I C
Geometría
INGENIO
INGENIO 255
1.
El primer jugador tomará como referencia uno de
los puntos dibujados como vértice, a fin de formar
una figura de cuatro lados en el menor tiempo
posible. (Fig. 2).
2. Al transcurrir el tiempo, si el jugador logró realizar
la tarea, cederá el turno al otro jugador.
Nos organizamos
6
LABORATORIO
F ORMAMO S
POLÍGONOS
Nombre Tiempo
1.
2.
3.
4.
TOTAL
Jugamos y aprendemos
1. Forma parejas de jugadores.
2. Dibuja en una hoja de papel 16 puntos
equidistantes. (Fig. 1).
3. Lancen la moneda para decidir quién
inicia el juego.
Gana el juego el jugador que
logra formar 5 cuadrados en
distintas posiciones y en el
menor tiempo.
(Fig. 1)
(Fig. 2)

256. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
256
TALLER
13
Un cuadrilátero es una figura geométrica de cuatro lados y cuatro ángulos.
ELEMENTOS
Lados: AB, BC, CD, AD
A
a
B
b
D
q
C
g
Ángulos: a, b, q, g
Vértices: A, B, C, D
CLASIFICACIÓN
Romboide
El romboide tiene dos pares de lados paralelos.
AB // CD y BC // AD
Se cumple:
AB = CD ^ BC = AD
Jardín
cocina
Baño
Sala
Sala
B
i
b
l
i
o
t
e
c
a
C
o
m
e
d
o
r
Habitación
1
Habitación
2
¿Cómo se llama
a las figuras de 4
lados?
CONCEPTO DE CUADRILÁTEROS
CUADRILÁTEROS
Observa el plano
de la casa.
Cada ambiente
forma una figura
de 4 lados.
A estas figuras se
las conoce como
cuadriláteros.
A
B C
D
a a
b
b

257. L U D O M A T I C
Geometría
INGENIO
INGENIO 257
Rombo Cuadrado Trapecio Rectángulo
La sala es un:
La cocina es un:
La habitación 2 es un:
El baño es un:
Rectángulo
Todos sus ángulos son rectos.
Se cumple:
A
B C
D
AB = CD
BC = AD
Rombo
Es el cuadrilátero con cuatro lados iguales.
Se cumple:
A
B
C
D
AB = BC = AD = DC
Cuadrado
Es el cuadrilátero con cuatro lados iguales y cuatro ángulos rectos.
Se cumple
A
B C
D
AB = BC = CD = AD
Trapecio
Es el cuadrilátero que tiene solo un par de lados paralelos (Bases).
A
B C
D
Se cumple
BC // AD
BC : Base menor
AD: Base mayor
Ejemplo: Del ejemplo anterior, observa el plano de la casa y marca con una x
la respuesta correcta.
b
b
a a
a
a
a
a
b
b
b b

258. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
258
Determina cuántos trapecios
observas en la imagen.
Resolución:
3 4
1 2
Observamos 4 trapecios, pues estos
cuadriláteros solo tienen un par de
lados paralelos.
Determina cuántos trapecios
observas en la imagen.
Resolución:
3 4
1 2
Observamos 4 trapecios, pues estos
cuadriláteros solo tienen un par de
lados paralelos.
ANALIZAMOS Y APRENDEMOS
Argumenta tu respuesta, al calcular el
valor de “x” si ABCD es un cuadrado.
16 cm
A
C
B
D
x + 2 cm
Resolución:
1)ABCD es un cuadrado.
2)Entonces:
AC = BD
x + 2 = 16
x = 14
3)El valor de “x” es 14.
Determina el valor de las siguientes
proposiciones:
1)
El rectángulo tiene 4 lados ( )
iguales y 4 ángulos rectos(90°).
2)
Un cuadrilátero es una figura ( )
geométrica de 4 lados.
3)
El rectángulo es un cuadrilátero( )
que tiene 4 ángulos rectos.
4)
El trapecio es un cuadrilátero ( )
que tiene 4 lados no paralelos.
Resolución:
1)
El rectángulo no tiene 4 lados
iguales, por lo tanto la proposición
es falsa.
2)
El cuadrilátero es una figura
geométrica de 4 lados, por lo tanto
la proposición es verdadera.
3)
El rectángulo es un cuadrilátero
que tiene 4 ángulos rectos, por lo
tanto la proposición es verdadera.
4)
El trapecio es un cuadrilátero que
tiene 2 lados paralelos, por lo tanto
la proposición es falsa.
Piero juega con su cometa. Esta tiene
forma de un . Argumenta tu
respuesta.
Resolución:
1)
Los cuatro lados de la cometa son
iguales.
2)
Los cuatro ángulos no son rectos.
3)
Por lo tanto, la cometa tiene la
forma de un rombo.
1 2
3
4

259. L U D O M A T I C
Geometría
INGENIO
INGENIO 259
PIENSO Y RESUELVO
AUTOEVALUACIÓN
Indicadores de evaluación
Reconozco los diferentes tipos de cuadriláteros.
Dibujo cuadriláteros.
Reconozco los cuadriláteros en objetos de mi entorno.
1
Jardín
cocina
Baño
Comedor
Sala
Habitación
Habitación
2
A
B
D
C
3
3x +2
A
B
D
C
20
4
Piero compró un tablero de una
mesa rectangular como la que se
muestra en el gráfico.
Si todo el contorno mide 240 cm,
¿cuál es el valor de “x”?
80 cm
(26 + 2x) cm

260. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
260
TALLER
CUADRILÁTEROS:
PROPIEDADES
14
1.
La suma de las medidas de los ángulos interiores es igual a 360º.
A
a
q
b
g
B
D
C
a + b + q + g = 360°
2.
La suma de las medidas de los ángulos exteriores es igual a 360º.
PROPIEDADES DE LOS CUADRILÁTEROS
Para ello, utilizamos las
siguientes propiedades.
¿Cómo calculamos
los ángulos en el
cuadrilátero?
Observa la forma de las
piedras que utilizaban
los incas para construir
sus templos.
x + y + w + z = 360°
A
B x
w
y
z
D
C
●
●
●
●

261. L U D O M A T I C
Geometría
INGENIO
INGENIO 261
ANALIZAMOS Y APRENDEMOS
Interpreta y calcula el valor del
ángulo que forma el parque ubicado
entre las calles Trinidad y Trinitarias.
Av. José María
Calle
B
Resolución:
a) Observamos que el parque tiene
la forma de un cuadrilátero.
90º + 90º + 108º + x = 360º
288º + x = 360º
x = 360º – 288º
x = 72º
c) El valor del ángulo formado por
las calles Trinidad y Trinitarias es
de 72º.
Interpreta y calcula el valor del
ángulo que forma el parque ubicado
entre las calles Trinidad y Trinitarias.
Av. José María
Calle
B
Resolución:
a) Observamos que el parque tiene
la forma de un cuadrilátero.
90º + 90º + 108º + x = 360º
288º + x = 360º
x = 360º – 288º
x = 72º
c) El valor del ángulo formado por
las calles Trinidad y Trinitarias es
de 72º.
1
Calcula el valor del cuarto ángulo
exterior.
Resolución:
a) Sabemos que la suma de los
ángulos exteriores de todo
cuadrilátero es de 360º.
b) Del gráfico, observamos tres
ángulos externos cuyos valores
son 85º, 78º, 75º y un ángulo
externo de valor no conocido al
que llamaremos “x”.
c) De lo anterior:
85º + 78º + 75º + x = 360°
238º + x = 360º
x = 360º – 238º
x = 122º
d) El valor del cuarto ángulo es de
122º
78°
75°
85°
2
x
Calcula la medida del cuarto ángulo
del cuadrilátero de boxeo. Comunica
tu respuesta.
Resolución:
a) Observamos que tres ángulos
internos del cuadrilátero miden
90º.
b) Sabemos que la suma de los
ángulos interiores de todo
cuadrilátero es de 360º.
c) De lo anterior
90º + 90º + 90º + x = 360º
270º + x = 360º
x = 360º – 270º
x = 90º
3
En la figura, calcula el valor de “x”.
Resolución:
a) Sabemos que la suma de los
cuatro ángulos internos de todo
cuadrilátero es 360º.
b) De lo anterior
2x + 30º + 5x + 15º + 2x – 10º + 3x – 11º
= 360º
12x + 24º = 360º
12x = 360º – 24º
12x = 336º
x = 28º
c) El valor de “x” es 28°.
5x + 15°
3x – 11°
2x – 10°
2x + 30°
4
x

262. 4.° primaria
L U D O M A T I C
INGENIO
INGENIO
262
a)
b)
c)
d)
a)
b)
c)
d)
AUTOEVALUACIÓN
PIENSO Y RESUELVO
1 2
3 4
90º
90º
90º
x
Indicadores de evaluación
Conozco las propiedades básicas de los cuadriláteros.
Utilizo las propiedades de los cuadriláteros en la
solución de problemas.

263. 1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de
4 estudiantes.

Elaboran un
mapa o croquis
de tu colegio.
Sobre el mapa elaborado,
identifican con un número cada
cuadrilátero. Luego, elaboran
un listado con los números que
usaron. Frente a cada uno de
éstos, escriben el nombre del
cuadrilátero.
Comparan,
discuten y
consolidan
los resultados
obtenidos.
1. Situación problemática
Nuestro contexto cotidiano esta rodeado de aplicaciones geométricas. Al desarrollarlas,
logramos que el estudiante esté mejor preparado para afrontar diversas situaciones
cotidianas usando la observación, interpretación y representación. Para reforzar estas
actitudes, es necesario reforzar la práctica. En este caso, siendo los cuadriláteros
tema de la Geometría, tienen aplicación práctica en el uso de mapas, planos y en la
elaboración de croquis para ubicarnos.
2. Finalidad
El alumno reconoce y nombra diversos cuadriláteros por su apariencia global en una
situación práctica.
3. Recursos materiales
Cartulina.
Lápices.
Borrador.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplenoportunamenteconlasfuncionesasignadas.
2 6 3
CUADRILÁTEROS
PROYECTO DE APRENDIZAJE N.0
6
263
INGENIO

264. INGENIO
4.° primaria
L U D O M A T I C
264
PERÍMETROS
Educación con equidad de géneros
Cultivamos Valores
•
Educación para
la equidad de
géneros.
•
Tolerancia.
Aprendemos a:
•
Determinar el perímetro de las figuras
geométricas.
•
Calcular el área de las regiones.
Observa la imagen y contesta.
¿Sabes qué es la igualdad de géneros?
¿Los hombres y mujeres tienen las mismas oportunidades?
7
UNIDAD

265. INGENIO
L U D O M A T I C
Geometría
265
1. Forma grupo de 4 integrantes.
2. Debes disponer de 12 fichas de pentominós.
(Ver fig. 1)
1.
Cada grupo debe armar y rellenar las
imágenes. (Ver fig. 2).
2.
Cuenta los lados de los cuadrados que
bordean la figura.
3.
Anota y conversa sobre la cantidad de lados
encontrados.
(Fig. 1)
Nos organizamos
Jugamos y aprendemos
Gana el juego, el grupo
que culmina primero la
actividad y argumenta los
resultados encontrados.
JUGANDO
CON PE NTOMI N ÓS
7
LABORATORIO
(Fig. 2)

266. INGENIO
266
UNIDAD DE MEDIDA:
LONGITUD
Son convenciones usado para establecer medidas; por ejemplo la altura de un árbol,
la longitud de una piscina, la longitud de una habitación, la altura de un edificio etc.
UNIDADES MENORES (SUBMÚLTIPLOS)
Hay unidades de medidas menores utilizadas para medir objetos pequeños como la
longitud de un libro, de una goma, de un alfiler, etc.
Unidad Submútiplos
Metro (m) Decímetro (dm) Centímetro (cm) Milímetro (mm)
UNIDAD DE MEDIDA
TALLER
15
Para
saberlo, me
colocaré
al costado
del
tallímetro.
¿Porqué el tallímetro?
Para medir longitudes,
se puede utilizar distintas
unidades de medida. La
unidad de medida más
utilizada es el metro (m).
¡Piero,
haz
crecido!
¿Cuánto
mides
ahora?

267. INGENIO
L U D O M A T I C
Geometría
267
km
hm
dam
m
dm
÷ 10
× 10 cm
mm
Unidad de equivalencia
1 metro = 10 decímetros (si dividimos el metro en 10 partes iguales,
cada parte es un decímetro).
1 metro = 100 centímetros (si dividimos el metro en 100 partes iguales,
cada parte es un centímetro).
1 metro = 1 000 milímetros (si dividimos el metro en 1 000 partes iguales,
cada parte es un milímetro).
UNIDADES MAYORES (MÚLTIPLOS)
También, hay unidades de medidas mayores que el metro. Se las utiliza para medir objetos
o distancias grandes: la distancia entre 2 ciudades, la longitud de un río, la altura de las
montañas, etc.
Unidad de equivalencia
1 kilómetro = 1000 metros.
1 hectómetro = 100 metros.
1 decámetro = 10 metros.
Múltiplos Unidad
Kilómetro (km) Hectómetro (hm) Decámetro (dam) Metro (m)

268. INGENIO
4.° primaria
L U D O M A T I C
268
Lee, interpreta y relaciona la medida
de longitud más adecuada para los
siguientes gráficos.
Resolución:
a) La unidad más precisa para medir
el borrador es el cm.
b) La unidad más precisa para medir
la moneda es el mm.
c) La unidad más precisa para medir
el escritorio es el m.
Lee, interpreta y relaciona la medida
de longitud más adecuada para los
siguientes gráficos.
Resolución:
a) La unidad más precisa para medir
el borrador es el cm.
b) La unidad más precisa para medir
la moneda es el mm.
c) La unidad más precisa para medir
el escritorio es el m.
Escribe y calcula las operaciones
para cada conversión.
a) 8 km a dam.
b) 5 cm a mm.
c) 50 m a km.
Resolución:
a)
Sabemos que la unidad km
es mayor al dam; por lo tanto,
multiplicamos por 10 dos veces.
Bajamos dos peldaños.
8 km a dam = 8 × 10 × 10 = 800 dam.
b)
Sabemos que la unidad cm
es mayor al mm; por lo tanto,
multiplicamos por 10 una vez.
Bajamos un peldaño.
5 cm a mm = 5 x 10 = 50 mm.
c)
Sabemos que la unidad m es
menor al km; por lo tanto, dividimos
entre 10 tres veces. Subimos tres
peldaños.
50m a km =50 :10:10:10 = 0,050 km.
Escribe y calcula las operaciones
para cada conversión.
a) 8 km a dam.
b) 5 cm a mm.
c) 50 m a km.
Resolución:
a)
Sabemos que la unidad km
es mayor al dam; por lo tanto,
multiplicamos por 10 dos veces.
Bajamos dos peldaños.
8 km a dam = 8 × 10 × 10 = 800 dam.
b)
Sabemos que la unidad cm
es mayor al mm; por lo tanto,
multiplicamos por 10 una vez.
Bajamos un peldaño.
5 cm a mm = 5 x 10 = 50 mm.
c)
Sabemos que la unidad m es
menor al km; por lo tanto, dividimos
entre 10 tres veces. Subimos tres
peldaños.
50m a km =50 :10:10:10 = 0,050 km.
ANALIZAMOS Y APRENDEMOS
Un autobús recorre 45 km en cada
viaje de Lima a Chosica. Si realiza
3 viajes de Ida y vuelta, ¿cuántos hm
recorrió?
Resolución:
a) Comprendemos el enunciado:
Viaje de ida = viaje regreso = 45 km
b) Planificamos y resolvemos:
• En el viaje de ida y vuelta a la
ciudad de Chosica, recorre
45 km + 45 km = 90 km
• En 3 viajes de ida y vuelta
,recorre 90 Km × 3 = 270 km
• Convirtiendo las unidades km a hm:
270 Km = 270 x 10 = 2700 hm
c) Comunicamos la respuesta.
El autobús recorrió 2 700 hm en los
3 viajes de ida y vuelta a Chosica.
Un autobús recorre 45 km en cada
viaje de Lima a Chosica. Si realiza
3 viajes de Ida y vuelta, ¿cuántos hm
recorrió?
Resolución:
a) Comprendemos el enunciado:
Viaje de ida = viaje regreso = 45 km
b) Planificamos y resolvemos:
• En el viaje de ida y vuelta a la
ciudad de Chosica, recorre
45 km + 45 km = 90 km
• En 3 viajes de ida y vuelta
,recorre 90 Km × 3 = 270 km
• Convirtiendo las unidades km a hm:
270 Km = 270 x 10 = 2700 hm
c) Comunicamos la respuesta.
El autobús recorrió 2 700 hm en los
3 viajes de ida y vuelta a Chosica.
Resuelveycomunicaturespuesta. Lucero,
Piero y Paola salen a correr. Lucero corre
800 m, Piero 1 km y Paola 7 hm. ¿Cuántos
metros corrieron entre los tres?
Resolución:
a)Comprendemos lo siguiente:
Lucero corre = 800m
Piero corre = 1km
Paola corre = 7hm
Nos piden el total de distancia en
metros que corrieron los tres.
b)Resolvemos, convirtiendo las
cantidades a metros.
Total = 800 m +1km + 7 hm
Total = 800 m + 1000 m + 700 m
Total = 2 500 m
c)
Comunicamos la respuesta: Lucero,
Piero y Paola corrieron 2 500 m entre los
tres.
Resuelveycomunicaturespuesta. Lucero,
Piero y Paola salen a correr. Lucero corre
800 m, Piero 1 km y Paola 7 hm. ¿Cuántos
metros corrieron entre los tres?
Resolución:
a)Comprendemos lo siguiente:
Lucero corre = 800m
Piero corre = 1km
Paola corre = 7hm
Nos piden el total de distancia en
metros que corrieron los tres.
b)Resolvemos, convirtiendo las
cantidades a metros.
Total = 800 m +1km + 7 hm
Total = 800 m + 1000 m + 700 m
Total = 2 500 m
c)
Comunicamos la respuesta: Lucero,
Piero y Paola corrieron 2 500 m entre los
tres.
km
hm
dam
m
dm
÷ 10
× 10 cm
mm
1
3 4
2

269. INGENIO
L U D O M A T I C
Geometría
269
h)
h)
d)
d)
1 2
3 4
Indicadores de evaluación
Reconozco las unidades de longitud.
Calculo longitudes en otras unidades.
Convierto unidades de longitud.
AUTOEVALUACIÓN
PIENSO Y RESUELVO

270. INGENIO
4.° primaria
L U D O M A T I C
270
PERÍMETROS
TALLER
16
En un cuadrado
L
L
L L
En un triángulo
b
a
c
PERÍMETRO
P = L + L + L + L
P = 2a + 2b
P = a + a + b + b
P = a + b + c
4 m 4 m
8 m
8 m
P = 4L
¿Cuánto de alambre
necesitamos para
cercar nuestro
biohuerto?
Paraello,necesitaremos,
conocer la medida de
los lados.
¿Qué es el perímetro? El perímetro de una figura
geométrica es la medida
de su contorno.
a
a
b b
En un rectángulo

271. INGENIO
L U D O M A T I C
Geometría
271
Se necesita cercar una piscina de
24 m de largo y 8 m de ancho. ¿Cuántos
metrosdesogasonnecesarioscomprar?
Resolución:
a) Graficamos.
24 m
24 m
8 m
8 m
b) Calculamos el perímetro.
P = 8 m + 24 m + 8 m + 24 m
P = 64 m
c) Es necesario comprar 64 m de
soga.
Se necesita cercar una piscina de
24 m de largo y 8 m de ancho. ¿Cuántos
metrosdesogasonnecesarioscomprar?
Resolución:
a) Graficamos.
24 m
24 m
8 m
8 m
b) Calculamos el perímetro.
P = 8 m + 24 m + 8 m + 24 m
P = 64 m
c) Es necesario comprar 64 m de
soga.
Representa gráficamente y calcula
el número de árboles que pueden
plantarse alrededor de un terreno
cuadrangular, cuyo perímetro mide
64 m. Cada árbol debe tener una
separación de 4 m y debe haber uno
en cada esquina.
Resolución:
Comprendemos que el perímetro
del terreno es 64 m.
Cada árbol está separado por 4 m.
b) Representamos gráficamente el
terreno cuadrangular.
P = 4L
64 = 4L
L = 64 ÷ 4
L = 16
c) Plantamos los árboles.
d) Comunicamos la respuesta. Se
puede plantar 14 árboles alrededor
del terreno.
Representa gráficamente y calcula
el número de árboles que pueden
plantarse alrededor de un terreno
cuadrangular, cuyo perímetro mide
64 m. Cada árbol debe tener una
separación de 4 m y debe haber uno
en cada esquina.
Resolución:
Comprendemos que el perímetro
del terreno es 64 m.
Cada árbol está separado por 4 m.
b) Representamos gráficamente el
terreno cuadrangular.
P = 4L
64 = 4L
L = 64 ÷ 4
L = 16
c) Plantamos los árboles.
d) Comunicamos la respuesta. Se
puede plantar 14 árboles alrededor
del terreno.
ANALIZAMOS Y APRENDEMOS
Calcular el perímetro de un triángulo
equilátero de lado igual a 16 cm.
Resolución:
a)
Sabemos que el triángulo
equilátero tiene 3 lados iguales.
b) Representamos gráficamente.
16 cm 16 cm
A B
B
16 cm
c) Planteamos el problema:
P = 16 cm + 16 cm + 16 cm
Þ P = 48 cm
d) El perímetro del triángulo
equilátero es 48 cm.
Calcular el perímetro de un triángulo
equilátero de lado igual a 16 cm.
Resolución:
a)
Sabemos que el triángulo
equilátero tiene 3 lados iguales.
b) Representamos gráficamente.
16 cm 16 cm
A B
B
16 cm
c) Planteamos el problema:
P = 16 cm + 16 cm + 16 cm
Þ P = 48 cm
d) El perímetro del triángulo
equilátero es 48 cm.
En un triángulo escaleno, sus lados
son 6 cm y 17 cm. Analiza y calcula
el valor del tercer lado si el perímetro
del triángulo es 43 cm.
Resolución:
a) Sabemos que un triángulo esca-
leno tiene 3 lados con medidas
diferentes.
b) El perímetro es la suma de
longitudes del contorno de la
figura.
c) P = 6 cm + 17 cm + x cm
43 cm = 23 cm + x cm
43 cm – 23 cm = x cm
x = 20 cm
En un triángulo escaleno, sus lados
son 6 cm y 17 cm. Analiza y calcula
el valor del tercer lado si el perímetro
del triángulo es 43 cm.
Resolución:
a) Sabemos que un triángulo esca-
leno tiene 3 lados con medidas
diferentes.
b) El perímetro es la suma de
longitudes del contorno de la
figura.
c) P = 6 cm + 17 cm + x cm
43 cm = 23 cm + x cm
43 cm – 23 cm = x cm
x = 20 cm
1 2
3 4
4 m 4 m 4 m 4 m
4 m
4 m
4 m
4 m
L
L
L
L

272. INGENIO
4.° primaria
L U D O M A T I C
272
AUTOEVALUACIÓN
PIENSO Y RESUELVO
1
Se necesita colocar grecas al borde
del siguiente cuadro. Si el metro
de greca cuesta S/. 2,50, ¿cuánto
pagaré por el total de greca a
necesitar? Comunica tu respuesta.
4 m
4 m
2 m
2 m
2
Observa y calcula el perímetro del
biohuerto.
40 m
32 m
24 m
3 En las siguientes figuras, determina
cuáles tienen igual perímetro.
II
I
4 cm
4 cm 4 cm
5 cm
6 cm
5 cm
6 cm
8 cm
5 cm
2 cm III IV
4
Indicadores de evaluación
Aprendo el concepto de perímetro.
Realizo cálculos sobre perímetros.
Resuelvo problemas utilizando el concepto de
perímetro.

273. INGENIO 273
TALLER
17
• Para ello, utilizaremos como unidad de medida cada cuadrado de césped.
1m
1m
• Cada cuadrado de césped equivale a un metro cuadrado (1 m2
).
Piero y Lucero han contado 96 cuadrados que es lo mismo que 12 m × 8 m = 96 m2
.
ÁREAS
12 m
8 m
¡Qué buena
iniciativa! ¿Sabes la
cantidad de césped
que necesitas?
Mis amigos y yo
queremos colocar
césped sintético en
el campo de fútbol
de la escuela.
ÁREAS DE FIGURAS GEOMÉTRICAS
h
b
Triángulo
A =
b × h
2
h
Romboide
A = b × h
h
h
b
b
Cuadrado
A = L × L Þ A = L2
L
L
Rectángulo
A = b × h
b
h
Donde:
b: base
h: altura
Donde:
L: lado
b/2

274. INGENIO
4.° primaria
L U D O M A T I C
274
Un terreno tiene la forma y las
medidas indicadas en el gráfico.
¿Cuánto mide el área construida?
Solución
a) Comprendemos el problema.
Observamos que el gráfico tiene
la forma de un triángulo y un
rectángulo juntos.
b) Planifico y ejecuto la solución.
C o n t a m o s e l n ú m e r o d e
cuadraditos del rectángulo.
Área del rectángulo = 24 =24 m2
Contamos el número
de cuadraditos en el
triángulo.
Área del triángulo = 6m2
Área total = Área rectangular +
Área triangular
c) Comunicamos la respuesta.
Área total = 24 + 6 = 30 =30 m2
Un terreno tiene la forma y las
medidas indicadas en el gráfico.
¿Cuánto mide el área construida?
Solución
a) Comprendemos el problema.
Observamos que el gráfico tiene
la forma de un triángulo y un
rectángulo juntos.
b) Planifico y ejecuto la solución.
C o n t a m o s e l n ú m e r o d e
cuadraditos del rectángulo.
Área del rectángulo = 24 =24 m2
Contamos el número
de cuadraditos en el
triángulo.
Área del triángulo = 6m2
Área total = Área rectangular +
Área triangular
c) Comunicamos la respuesta.
Área total = 24 + 6 = 30 =30 m2
ANALIZAMOS Y APRENDEMOS
Del problema anterior, calcula el
valor del área mediante fórmulas.
Solución
a)
Aplicamos la fórmula y resolvemos.
A = b × h
A = 8 m × 3 m
A = 24 m2
b) Aplicamos la fórmula y resolvemos.
A = b × h/2
3 m × 4 m
2
A = Þ A = 6 m2
De a) y b)
Atotal
= A + A
Atotal
= 24 m2
+ 6 m2
Atotal
= 30 m2
c) Comunicamos la respuesta.
Área total es 30 cm2
.
Calcula el valor de la suma de ambas
áreas de las figuras.
Resolución:
a) Calculamos A1
A1
= b × h Þ A1
= 6 m × 3 m
A1
= 18 m2
b) Calculamos A2
4 m × 4 m
2
A2 = A2
= 8 m2
c) Sumamos las áreas.
A1
+ A2
= 18 m2
+ 8 m2
A1
+ A2
= 26 m2
4 m
8 m
3 m
3 m
A1
A2
Al colocar mayólica en la sala de mi casa,
un albañil cobra S/. 20 el metro cuadrado.
¿Cuánto pagaré por el trabajo del
albañil?
Resolución
a) Comprendemos el problema.
La sala tiene forma rectangular.
b) Costo por el metro cuadrado = S/. 20
Tenemos 21 metros cuadrados.
Entonces: 21× 20 = 420
c) Comunicamos el resultado.
Pagaré 420 soles por el trabajo del
albañil.
6 m 4 m
4 m
A1
A2
3 m
7 m
3 m
1
3 4
2

275. INGENIO
L U D O M A T I C
Geometría
275
AUTOEVALUACIÓN
PIENSO Y RESUELVO
1
a + 4
2a – 2
4
2
3 4
Indicadores de evaluación
Aprendo las principales fórmulas de áreas.
Calculo el valor de áreas en diferentes gráficos.
Resuelvo problemas sobre áreas.

276. 1. Situación problemática
Varias aplicaciones básicas de la geometría involucran el cálculo de la suma de
los lados de un polígono (mejor conocido como su perímetro), y la superficie total
comprendida por sus lados (mejor conocido como su área). Ambos conceptos los
usamos cuando se desea conocer cuántos metros de alambre son necesarios para
rodear una parcela de jardín, el total de metros de cinta para bordear un mantel,etc.
2. Finalidad
Aplicarlos conocimientos sobre el cálculo de áreas y perímetros en la resolución de
problemas de la vida diaria.
3. Recursos materiales
Hojas bond. Goma, tijera.
Lápices. Borrador.
4. Etapas y actividades
5. Evaluación
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
PROYECTO DE APRENDIZAJE N.0
7
PERÍMETROS
1.ª etapa 2.ª etapa 3.ª etapa

Forman grupos de 4
estudiantes.
Se necesita enrejar el colegio
que tiene forma rectangular
con 45m de ancho y 50 metros
de largo. ¿Cuántos metros de
rejas será necesario comprar?
¿Cuánto se pagará por la
mano de obra del enrejado?
Traen un presupuesto
sobre el costo de la
reja.
Traen un presupuesto
sobre la mano de obra
para la colocación de
la reja.
Realizan el presupuesto
de la obra.
Presentan
y exponen
sus
trabajos.
INGENIO
276

277. Cultivamos Valores
•
Educación para el
éxito.
•
Respeto.
Aprendemos a
•
Reconocer los elementos básicos de
los poliedros.
•
Calcular el volumen de los sólidos
geométricos.
• Construir poliedros y cuerpos redondos.
SÓLIDOS
GEOMÉTRICOS
Educación para el éxito
UNIDAD
8
Observa la imagen y contesta.
¿Es necesario la perseverancia para lograr el éxito?
¿Qué debo hacer para triunfar en la vida?

278. INGENIO
4.° primaria
L U D O M A T I C
278
1.
Unir los palillos pegando los vértices con el
Limpiatipos. (Fig. 1). El grupo argumentará sobre
el sólido geométrico formado.
2.
Unir los palillos de acuerdo a la fig. 2. El grupo
conversará sobre el sólido geométrico formado.
Fig. 1
Fig. 2
8
LABORATORIO
C O N S T R U Y E N D O
P O L I E D R O S
Gana el equipo que finaliza
primero los diseños y argumenta
lo trabajado.
Nos organizamos
1. Forma grupo de 4 integrantes.
2. Cada grupo se responsabilizará de traer
consigo palillos para brochetas de 8 cm y
limpiatipos o plastilinas.
Jugamos y aprendemos

279. INGENIO
L U D O M A T I C
Geometría
279
POLIEDROS Y CUERPOS
REDONDOS
TALLER
18
POLIEDROS
La pirámide y el prisma son sólidos geométricos formados por caras poligonales.
Pirámide Prisma
POLIEDROS Y CUERPOS REDONDOS
Mira, Lucerito: las
caras de las cajas
de regalo tienen
forma rectangular.
¡Oh sí! ¿qué
pasa con las
bombillas?
¿Las bombillas son
cuerpos redondos?
¡Así es! los cuerpos
geométricos se
clasifican en Poliedros
y cuerpos redondos.

280. INGENIO
4.° primaria
L U D O M A T I C
280
ELEMENTOS DE UN PRISMA Y UNA PIRÁMIDE
base
vértice
base
cara
lateral
(altura)
h
cara
lateral
altura
base
Prisma Pirámide
CUERPOS REDONDOS
Son sólidos geométricos que tiene, al menos, una de las caras o superficies de forma curva
como el cono, el cilindro y la esfera.
Cilindro Cono Esfera
Ejemplo:
Relaciona cada objeto con la forma del sólido geométrico que lo representa.
Observación
Ten en cuenta que si las caras laterales de los
poliedros son triángulos, se llaman pirámides;
pero si son paralelogramos, se llaman prismas.

281. INGENIO
L U D O M A T I C
Geometría
281
ANALIZAMOS Y APRENDEMOS
¿Cuántos vértices tiene el poliedro?
Argumenta tu respuesta.
Resolución:
a) Representamos.
1
2
4
5
6
7
8
3
b) Argumentamos.
El poliedro tiene 8 vértices, las
mismas que son la unión de las
aristas.
Reconoce y pinta las dos bases del
prisma triangular.
Resolución:
2
Cuántas caras laterales tiene la
pirámide? Argumenta tu respuesta.
Resolución:
a)
Gráficamente
1
4
2
3
2
4
3
1
b)
Observamos que la pirámide tiene
4 caras laterales.
3 4
Identifica y argumenta el tipo de
sólido que representa cada imagen.
Resolución
b)
El cono es la representación
geométrica de la gorra, pues tiene
una superficie curva y un vértice.
c)
El cilindro es la representación
geométrica del tomatodo, pues
tiene una superficie curva y dos
bases circulares.
Identifica y argumenta el tipo de
sólido que representa cada imagen.
Resolución
b)
El cono es la representación
geométrica de la gorra, pues tiene
una superficie curva y un vértice.
c)
El cilindro es la representación
geométrica del tomatodo, pues
tiene una superficie curva y dos
bases circulares.
1
a)
El prisma es la representación
geométrica del ladrillo, pues sus
caras laterales son paralelogramos.

282. INGENIO
4.° primaria
L U D O M A T I C
282
PIENSO Y RESUELVO
AUTOEVALUACIÓN
Indicadores de evaluación
Reconozco los principales sólidos geométricos.
Reconozco los sólidos geométricos en objetos de mi
entorno.
Reconozco los elementos de un poliedro.
Relaciona la imagen de los sólidos y
sus características.
a) Tiene solo superficie curva.
b) Tiene dos bases.
c) Tiene caras planas.
d) Tiene un vértice.
3 Observa y marca las imágenes que
tienen una parte en forma de cono
4
1
a)
a)
2

283. INGENIO
L U D O M A T I C
Geometría
283
VOLUMEN DE LOS SÓLIDOS
GEOMÉTRICOS
TALLER
19
Leche Gloria Leche Ideal
La pila de latas de
leche Gloria ocupa
mayor espacio.
Pues, yo creo que la pila
de latas de leche Ideal,
ocupa mayor espacio.
¿Cómo sabemos la
cantidad de espacio
que ocupan?
¡Fácil! Para ello, debemos
determinar el volumen,
el cual es el espacio que
ocupa un cuerpo.
A
h
Prisma
V = Área de la base × h
Donde h es altura.
A
h
Pirámide
V = Área de la base × h
1
3
VOLUMEN

284. INGENIO
4.° primaria
L U D O M A T I C
284
Ejemplo 1
La caja de base cuadrada tiene una altura de 30 cm. Si la arista de la base mide 20 cm,
calcula el volumen de la caja.
Resolución:
a) Sabemos que:
V = área de la base × altura
b) Calculamos el área de la base cuadrada.
1) A = L2
2) A = (20 cm)2
3) A = 400 cm2
c) Calculamos el volumen.
1) V = Área de la base × h
2) V = 400 cm2
× 30 cm3
3) V = 12 000 cm3
d) Comunicamos la respuesta.
El volumen de la caja es de 12 000 cm3
.
Ejemplo 2
La arista básica y la altura de una pirámide de base cuadrada miden 25 cm y 33 cm
respectivamente. Calcula el volumen de la pirámide.
a) Sabemos que:
V =
1
3
área de la base × h
b) Calculamos el área de la base cuadrada.
• AB
= L2
= (25 cm)2
= 625 cm2
c) Calculamos el volumen.
• V = 1
3
área de la base × h
V = 1
3
625 cm2
× 33 cm
V =
V = 6 875 cm3
d) Comunicamos la respuesta.
El volumen de la caja es de 6 785 cm3
.
33 cm
25 cm
30 cm
20 cm
20 625 cm3
3

285. INGENIO
L U D O M A T I C
Geometría
285
ANALIZAMOS Y APRENDEMOS
Analiza y argumenta la afirmación
correcta.
(II)
(I)
a) La construcción I tiene mayor
volumen.
b) La construcción II tiene mayor
volumen.
c) La construcción I y II tienen igual
volumen.
Resolución:
a) Sabemos que:
El volumen de un cuerpo es el
espacio que este ocupa.
b)
Observamos que la construcción
I y II están formados por 6 cubos.
1 1
2 2 3
3 4 4
5 5
6 6
c)
Por lo anterior, ambas
construcciones ocupan igual
espacio.
d)
Por lo tanto, la construcción I y II
tienen igual volumen.
Grafica y calcula el volumen de un
prisma cuadrangular, si el área de
su base es de 16 cm2
y la altura mide
8 cm.
Resolución:
a) Resolvemos.
b) Resolvemos.
V = Área de la base × h
V = 16 cm2
× 8 cm
V = 128 cm3
16 cm2
8 cm
1 2
4
Determina el volumen de la cajita de
frugos de base cuadrada.
Comunica tu respuesta.
FRUGOS frugo
Resolución
a) Sabemos que:
b) Calculamos el área de la base
cuadrangular.
A = L2
Þ = (8 cm)2
A = 64 cm2
c) Calculamos el volumen de la
pirámide.
V = (64 cm2
) × (12 cm)
V = 256 cm3
d) Comunicamos el resultado.
El volumen de la cajita de frugos
es 256 cm3
.
Determina el volumen de la cajita de
frugos de base cuadrada.
Comunica tu respuesta.
FRUGOS frugo
Resolución
a) Sabemos que:
b) Calculamos el área de la base
cuadrangular.
A = L2
Þ = (8 cm)2
A = 64 cm2
c) Calculamos el volumen de la
pirámide.
V = (64 cm2
) × (12 cm)
V = 256 cm3
d) Comunicamos el resultado.
El volumen de la cajita de frugos
es 256 cm3
.
V = 1
3
área de la base × h
V = 1
3
área de la base × h
1
3
Grafica y calcula el volumen de una
pirámide, si el área de la base es
18 cm2
y de altura 10 cm.
Resolución:
a) Graficamos.
b) Resolvemos.
V = (18 cm2
)· 10 cm
V = 60 cm3
10 cm
18 cm2
3
1
3
1
3
V = área de la base × h
1

286. INGENIO
4.° primaria
L U D O M A T I C
286
AUTOEVALUACIÓN
PIENSO Y RESUELVO
1
Indicadores de evaluación
Aplico la fórmula en la resolución de sólidos
geométricos.
Resuelvo problemas sobre volúmenes de sólidos
geométricos.
Grafica y calcula el volumen de un
prisma cuadrangular, cuyo perímetro
de base cuadrada es 16 cm y una
altura de 6 cm.
2
En los siguientes gráficos, ¿cuál de los
depósitos tienen mayor volumen.
1 cm
2 cm
16 cm
4 cm
3 cm
2
c
m
6 cm
3 cm
2
c
m
3
Si el volumen de un prisma es 64 cm3
y el área de su base es de 16 cm2
,
calcula la medida de la altura del
prisma.
4

287. PROYECTO DE APRENDIZAJE N.0
8
1. Situación problemática
Sabemos que todo lo que ocupa un lugar en el espacio se llama cuerpo. Por ejemplo:
un libro, un borrador, etc. La extensión del lugar ocupado por este cuerpo se llama
volumen. La capacidad es lo que cabe dentro de un objeto.
Ejemplo:
1 dm3 1 dm3
2. Finalidad
Aplicar los conocimientos sobre el cálculo de áreas y perímetros en la resolución de
problemas de la vida diaria.
3. Recursos materiales
Hojas cuadriculadas. Lápices.
Borrador.
4. Etapas y actividades
Indicadores de evaluación
Participan en el desarrollo de todas las etapas del
proyecto.
Aceptan con respeto las ideas de sus compañeros.
Cumplen oportunamente con las funciones asignadas.
SÓLIDOS GEOMÉTRICOS
1.ª etapa 2.ª etapa 3.ª etapa
Forman grupos de 4 estudiantes.
Tenemos el siguiente problema:
Un acuario tiene 0.80 m de largo, 0.6
m de ancho y 0.4m de profundidad.
¿Cuántos litros de agua serán
necesarios para llenarla?
¿Cúantospececitospodemoscolocar
como máximo si se recomienda 1
pececito por cada 4 litros de agua?

Plantean y resuelven las
preguntas:
•
¿De qué trata el
problema?
• ¿Qué datos tengo?
•
¿
Qué forma tiene la
piscina y cuáles son
sus dimensiones?
•
¿
Q u é t e p i d e e l
problema?
Elabora unplanderesolución.
Ejecutan el plan de
solución.
Comparan,
discuten y
consolidan
los
resultados
obtenidos.
5. Evaluación
INGENIO