Este documento presenta el plan de estudios del curso de Microeconomía I dictado por el profesor Sergio Monsalve en el semestre II de 2012. El curso tiene como objetivo principal presentar los conceptos básicos de la microeconomía neoclásica y analizar el comportamiento de hogares, empresas y mercados bajo diferentes estructuras como la competencia perfecta, monopolio y oligopolio. El curso consta de 13 clases magistrales y talleres semanales que abordan temas como la teoría del consumidor, producción, costos, equilibrio de mercado y fallas

1. MICROECONOMÍA I
(CÓDIGO 2016017)
GRUPOS 1 Y 3
SERGIO MONSALVE
SEMESTRE
II
DE 2012
1

2. OBJETIVO GENERAL DEL CURSO
EL OBJETIVO DE ESTE CURSO ES PRESENTAR UNA VISIÓN
INTRODUCTORIA A LA MICROECONOMÍA DESDE LA PERSPECTIVA NEOCLÁSICA, ADVIRTIENDO QUE PRESENTAR
UNA TEORÍA NO QUIERE DECIR QUE SE APRUEBA; POR EL
CONTRARIO, EL OBJETIVO BUSCADO EN ESTE CASO, ES
PERMITIR AL ESTUDIANTE EJERCER SU ESPÍRITU CRÍTICO,
CON CONOCIMIENTO DE CAUSA.
2

3. MÁS ESPECÍFICAMENTE, NUESTRO ESTUDIO EN EL
CURSO BUSCA:
I)
EN PRIMER LUGAR,
ENTENDER EL COMPORTAMIENTO DE
LOS HOGARES (CONSUMIDORES) Y LAS EMPRESAS (FIRMAS) EN UN AMBIENTE DE “COMPETENCIA PERFECTA”.
II) EN SEGUNDO LUGAR, ESTUDIAR LA NOCIÓN DE
EQUILIBRIO PARCIAL DE MERCADO Y SU EFICIENCIA.
III) FINALMENTE,
ESTUDIAR LAS “FALLAS DE MERCADO” (ES
DECIR, CUANDO EL EQUILIBRIO PARCIAL YA NO ES
EFICIENTE) DENTRO DE DIFERENTES ESTRUCTURAS DE
MERCADO TALES COMO EL MONOPOLIO, EL OLIGOPOLIO
Y LA COMPETENCIA MONOPOLÍSTICA.
3

4. ES DECIR, EL CURSO DE MICROECONOMÍA I
CONSISTE EN TRATAR DE CONSTRUIR UN
SISTEMA DE REFERENCIA QUE NOS PERMITA
ESTUDIAR LA ECONOMÍA AGREGADA (O,
MÁS ESPECÍFICAMENTE, LOS MERCADOS) A
PARTIR DEL COMPORTAMIENTO INDIVIDUAL
DE LOS AGENTES.
ESTO, EN PRINCIPIO, SE DIFERENCIA DEL
INTENTO DE LA MACROECONOMÍA I , QUE
BUSCA EL MISMO OBJETIVO, PERO MEDIANTE VARIABLES AGREGADAS A PRIORI.
4

5. METODOLOGÍA DEL CURSO
Se dictarán dos clases presenciales semanalmente:
1. La clase magistral del martes dictada por el
profesor titular de la materia.
2. Las clases de taller del miércoles (grupo 03) , del
jueves (grupo 01) y del viernes (grupo 02), cada una
con su correspondiente profesor auxiliar. Los
ejercicios realizados por el profesor auxiliar en el
taller serán previamente asignados por el profesor
titular.
5

6. PROFESORES AUXILIARES Y
MONITORES
Grupo 01 (Ma-Jue): Salomón Bechara.
Grupo 03 (Ma-Mie): Mabel Moreno.
Monitores: Julián Villamil y Adrián
Zuur.
Asistente: Carlos Guisa
6

7. PROGRAMA DEL CURSO
CLASE MAGISTRAL #1: NOCIONES BÁSICAS DE
LA MICROECONOMÍA: SU ORIGEN, OBJETIVOS
Y MÉTODOS.
CLASE
MAGISTRAL #2:
PRINCIPIOS DE
MAXIMIZACIÓN
LA
TEORÍA DEL CONSUMO.
DE
LA UTILIDAD Y MINIMIZACIÓN DEL GASTO.
CLASE MAGISTRAL #3: TIPOS DE MERCANCÍAS Y
LA NOCIÓN DE ELASTICIDAD.
CLASE MAGISTRAL #4:
EFECTO SUSTITUCIÓN.
EFECTO
INGRESO Y
7

8. CLASE MAGISTRAL #5: PRINCIPIOS DE LA TEORÍA
DE LA PRODUCCIÓN. MAXIMIZACIÓN DEL BENEFICIO (I).
CLASE MAGISTRAL #6: MAXIMIZACIÓN DEL
BENEFICIO (II). MINIMIZACIÓN DE COSTOS (I).
CLASE MAGISTRAL #7: MINIMIZACIÓN DE COSTOS
(II). EQUILIBRIO PARCIAL COMPETITIVO.
CLASE
MAGISTRAL #8:
EQUILIBRIO PARCIAL
COMPETITIVO CENTRALIZADO Y ÓPTIMOS DE
PARETO. INTRODUCCIÓN A LA TEORÍA DE
FALLAS DE MERCADO.
8

9. CLASE MAGISTRAL #9: MONOPOLIO Y MONOPSONIO.
CLASE MAGISTRAL #10:
MONOPOLÍSTICA.
OLIGOPOLIO Y COMPETENCIA
CLASE MAGISTRAL #11: INTRODUCCIÓN A LA TEORÍA DE
LOS BIENES PÚBLICOS Y LAS EXTERNALIDADES.
(OPCIONAL).
CLASE MAGISTRAL #12: MERCADO BAJO INCERTIDUMBRE: LA HIPÓTESIS DE LA UTILIDAD ESPERADA.
INFORMACIÓN ASIMÉTRICA.
CLASE MAGISTRAL #13: DOS ESTUDIOS PARCIALES
APLICADOS AL CASO COLOMBIANO.
9

10. BIBLIOGRAFÍA
Textos Básicos
1. Varian, Hal (2007), “Microeconomía Intermedia”. Antoni Bosch Editor.
2. Parkin, Michael, G. Esquivel & M. Ávalos (2006). “Microeconomía. Versión para América Latina” . Editorial
Pearson.
3. Monsalve, Sergio (editor) (2010), “Matemáticas Básicas
para Economistas”, Vol. II (Cálculo). Editorial Universidad Nacional.
4. Artículos que serán entregados oportunamente.
10

11. Textos Complementarios
1. Krugman, Paul & Robin Wells (2006),“Introducción a la
Microeconomía”. Editorial Reverté.
2. Stiglitz, Joseph (1994), “Principios de Microeconomía”.
Editorial Ariel.
3. Nicholson, Walter (2005), “Teoría Microeconómica”. Editorial Thomson.
4. Guerrien, Bernard & Sophie Allais (2009), “Microeconomia:
Una Presentación Crítica”. Maia Ediciones.
5. Marshall, Alfred (1898), “Principles of Economics”, Fourth
Edition, London, MacMillan.
11

12. PRERREQUISITO SUGERIDO
HABER APROBADO EL CURSO
DE CÁLCULO DIFERENCIAL
12

13. EVALUACIÓN
1.
Se realizarán tres parciales conjuntos (25% cada uno) en
las clases de los martes. El primer parcial evaluará
desde la clase magistral #1 hasta la #4; el segundo
parcial evaluará desde la clase magistral #5 hasta la
clase magistral #8; y el tercer parcial evaluará desde la
clase magistral #9 hasta la #12. Los tres parciales
tendrán la modalidad de test (selección múltiple).
2.
Una nota de talleres (25%) (tres talleres), realizados
en las clases de los miércoles (grupo 03), y de los jueves
(grupo 01). Estos talleres se realizarán en grupos
de, máximo, cuatro estudiantes.
13

14. -CORREO ELECTRÓNICO:
smonsalveg@unal.edu.co
-OFICINA: EDIFICIO 311,
CUARTO PISO, 5B.
-HORAS DE OFICINA: JUEVES, DESDE
UN POCO ANTES DE LAS 11 AM. HASTA
LAS 12:30 P.M., O SOLICITAR CITA
POR CORREO ELECTRÓNICO.
14

15. CLASE MAGISTRAL # 1
NOCIONES BÁSICAS DE LA
MICROECONOMÍA NEOCLÁSICA:
SU ORIGEN, SUS OBJETIVOS
Y SUS MÉTODOS
15

16. ¿QUÉ ES ECONOMÍA
NEOCLÁSICA?
ES LA VISIÓN GENERAL DE QUE:
LA ECONOMÍA ES UNA CIENCIA
NATURAL
CON LA MISMA CATEGORÍA DE LA FÍSICA O DE
LA BIOLOGÍA DE LOS SIGLOS XVII, XVIII y XIX.
16

17. Y, POR LO TANTO , LA DEBEN REGIR LOS MISMOS
PRINCIPIOS:
i)
Los sistemas están conformados por partículas.
ii)
Estas partículas se rigen por fuerzas emanadas del
Principio de Mínima Acción que afirma que:
“ La naturaleza es económica en todas sus
acciones"
iii) Las partículas se estabilizan alrededor de ciertos
estados de equilibrio del sistema.
17

18. iv) La metodología de investigación consiste en,
inicialmente, estudiar el sistema “sin rozamientos”, para después incorporar éstos, uno a
uno, y así asimilar el funcionamiento del sistema económico completo.
18

19. Pero… ¿Y por qué es tan importante el
“Principio de Mínima Acción”?
Este principio es una afirmación acerca de la
naturaleza del movimiento que permite
replantear la mecánica clásica de una manera
más general y potente que las mismas leyes
de Newton. Además, ha servido como
principio básico en la teoría de la relatividad,
en la mecánica cuántica y en la física de
partículas. Con ello, el Principio de Mínima
Acción está en el corazón de buena parte de la
física teórica contemporánea.
19

20. Ejemplos y Aplicaciones del “Principio de
Mínima Acción”
a) Pierre de Fermat (1601-1665) mostraba que los
rayos de la luz, en situaciones ópticas tales como la
refracción y la reflexión, seguían un principio de
menor tiempo (Principio de Fermat).
b) La línea recta que forma un rayo de luz en el vacío.
La forma esférica de una burbuja.
d) Eficiencia en los organismos (Darwin). Por
ejemplo, la “simetría” del cuerpo humano, etc.
c)
20

21. Ley de Snell (1627): Minimización del tiempo recorrido por la luz al
pasar
de un medio físico a otro.
Tomado de Wikipedia (DRA)
21

22. Si calculamos la acción de una pelota
moviéndose en el vacío con una velocidad
constante, veremos que la trayectoria que
sigue es la que consume el menor tiempo
posible, la cual coincide con una línea recta.
Velocidad constante en el vacío
Es lo que hacen las partículas de un rayo de luz
en el vacío: un rayo de luz es un ejemplo ideal
de una línea recta.
22

23. Teorema de Plateau:
Minimización de la
cantidad de superficie
jabonosa que contiene
una cantidad de aire
dada.
Tomado de Wikipedia (DRA)
23

24. Teorema de Plateau:
Minimización de la
cantidad de superficie
jabonosa limitada por
una forma específica.
Tomado de Wikipedia (DRA)
24

25. Teorema de Plateau:
Minimización de la
cantidad de
superficie jabonosa
limitada por una
forma específica.
Tomado de Wikipedia (DRA)
25

26. Teorema de Plateau:
Minimización de la
cantidad de superficie
jabonosa limitada por
una forma específica.
Tomado de Wikipedia (DRA).
26

27. Pueden observar muchos más de estos experimentos con burbujas en:
http://www.youtube.com/watch?v=5oRxjO54Zdk
27

28. Simetría en
el cuerpo
humano
como
resultado de
optimización
(adaptación)
de la biología
evolutiva
28

29. Aún más: en los animales, una falta sutil de
simetría puede reflejar un pobre desenvolvimiento dentro del ambiente de vida, y
esto se relaciona con bajo nivel de
sobrevivencia, mala salud y escasa descendencia futura.
29

30. Otro ejemplo de optimización de la biología
evolutiva
La división estable 50%- 50% (aproximadamente) entre hombres y mujeres de una población
grande, se ha demostrado que es el resultado
de la necesidad de adaptación biológica
evolutiva en búsqueda de la sobrevivencia.
30

31. ¿Y DE QUÉ MANERA ADAPTARON LA ECONOMÍA
PARA VERLA COMO UNA CIENCIA NATURAL?
31

32. Esta adaptación se llevó a cabo, fundamentalmente, durante la segunda mitad del siglo
XIX. Es decir,
La economía neoclásica se fundó
durante la segunda mitad del siglo
XIX y se desarrolló durante el siglo
XX.
32

33. Sus más importantes pioneros fueron: Léon Walras
(1834-1910), William Jevons (1835-1882),Carl
Menger (1840-1921) y Alfred Marshall (1842-1924).
Aunque cabe advertir que no todos ellos
coincidían en las mismas premisas de creación
del paradigma neoclásico, ni tampoco todos
fueron conscientes de que estaban facilitando la
creación de un nuevo esquema para pensar la
economía y hacer de ella una ciencia.
33

34. PIONEROS
Carl Menger (1840-1921)
“Principles of
Political Economy” (1871)
Fotos tomadas de Wikipedia (DRA).
William Jevons (1835-1882)
“The Theory of
Political Economy” (1871)
34

35. PIONEROS
Léon Walras (1834-1910)
“Éléments d’Économie Politique Pure” (1874)
Fotos tomadas de Wikipedia (DRA).
Alfred Marshall (1842-1924)
“Principles of Economics” (1890)
35

36. Quizás el más decidido en esto fue Léon
Walras:
“Las matemáticas serán la lengua especial para
hablar de hechos cuantitativos, y en consecuencia la economía será una ciencia matemática con
el mismo título de la mecánica y la astronomía”
(L. Walras, 1909)
36

37. Pero también Jevons así lo creía:
“La Teoría de la Economía (…) muestra una cercana
analogía con la Mecánica Estática, y se encuentra que las
Leyes de Intercambio son semejantes a las Leyes de
Equilibrio de una palanca determinadas por el principio
de las velocidades virtuales. La naturaleza de la Riqueza
y el Valor se explica considerando cantidades infinitamente pequeñas de placer y dolor, así como la Teoría de
la Estática se apoya en la igualdad de cantidades
infinitamente pequeñas de energía”.
(W. S. Jevons, 1871)
37

38. Por su parte, Carl Menger (1871) afirmaba en la Introducción
de sus Principios:
Juzgar los resultados a que nos ha conducido el (…) método de
investigación [[natural]], decidir si hemos logrado exponer
con éxito el hecho de que los fenómenos de la vida económica
se gobiernan por unas leyes estrictas similares a las que
rigen en la naturaleza, es cosa que corresponde a nuestros
lectores. Tan sólo querríamos prevenir aquí contra la
opinión de quienes niegan la regularidad de los fenómenos
económicos aludiendo a la libre voluntad de los
hombres, porque por este camino lo que se niega es que las
teorías de la economía política niegan el rango de ciencia
exacta.
38

39. Si, y bajo qué condiciones, una cosa es útil para mí; si, y
bajo qué condiciones, es un bien; si, y bajo qué
condiciones, es un bien económico; si, y bajo qué
condiciones, tiene valor para mí y cuál es la medida
de este valor; si, y bajo qué condiciones, se produce un
intercambio económico de bienes entre dos agentes
económicos y cuáles son los límites dentro de los
cuales puede llegarse a la formación del precio, todas
estas y otras muchas cuestiones son tan
independientes de mi voluntad como las leyes de la
química son independientes de la voluntad de un
químico práctico.
(Carl Menger, 1871)
39

40. Por su parte, Marshall creía más en la biología como paradigma epistemológico lo que requeriría de que fuera suplementada con investigación sociológica, histórica e institucional: :
“En los últimos estadios de la economía, cuando nos estamos
aproximando a las condiciones de la vida, las analogías biológicas
son preferidas a las mecánicas.” (…)
“La Meca del economista está en la biología económica más que en
dinámica económica. Sin embargo, los conceptos biológicos son más
complejos que los de la mecánica.”
(Alfred Marshall, 1890)
40

41. En el estudio del mercado desde la perspectiva
neoclásica:
1. Las “partículas” (agentes) de una Economía
son:
a) Los consumidores (hogares)
b) Los productores (empresas o firmas)
de bienes y servicios.
Este es el principio básico de lo que se conoce
como “individualismo metodológico”.
41

42. 2. El “Principio de Mínima Acción” (optimización) de una Economía consta de dos partes:
a) Los consumidores maximizan s u satisfacción
en el consumo.
b) Los productores maximizan el beneficio.
42

43. COMO VEREMOS, EL “PRINCIPIO DE MÍNIMA
ACCIÓN” (OPTIMIZACIÓN) EN UNA ECONOMÍA
CONDUCE A LA NOCIÓN DE MARGINALIDAD.
POR ELLO, AL ORIGEN DE LA ECONOMÍA
NEOCLÁSICA TAMBIÉN LO LLAMAN “REVOLUCIÓN MARGINALISTA”.
43

44. 3. POR SU PARTE, EL CONCEPTO BÁSICO DE
EQUILIBRIO DE UNA ECONOMÍA ES:
OFERTA DE BIENES
=
DEMANDA DE BIENES
Dibujo tomado de Wikipedia (DRA).
44

45. En resumen: la ECONOMÍA NEOCLÁSICA
está basada en tres principios:
1.
INDIVIDUALISMO METODOLÓGICO
2. OPTIMIZACIÓN
3. NOCIÓN DE EQUILIBRIO
45

46. Sin embargo, debemos tener en cuenta que:
“Nuestros hechos no son permanentes, ni repetibles, como los hechos de las ciencias naturales;
cambian incesantemente, y cambian sin repetición”.
(J. R. Hicks (1975))
46

47. Las Nociones de Competencia
Perfecta e Imperfecta
La Economía Neoclásica vista como una ciencia
natural, atacó, de manera principal, el problema
del funcionamiento del sistema del mercado de
bienes y servicios. Y lo hizo a la manera de la
Física: primero estudiando el sistema “sin rozamientos” y luego “con rozamientos”.
47

48. Y, en principio, asimiló esto de la siguiente forma:
Sistema sin rozamientos  Mercado bajo
competencia perfecta.
Sistema con rozamientos  Mercado bajo
competencia imperfecta.
48

49. ¿ Y en qué consiste un “Mercado bajo
Competencia Perfecta” ?
Permitamos que Walras, en sus “Elementos de Economía
Política Pura” de 1874, nos lo explique:
“(…) Los mercados mejor organizados desde el punto de
vista de la competencia son aquellos en que las ventas y
las compras se hacen mediante subasta, a través de
agentes tales como los agentes de cambio, corredores de
comercio o voceadores que las centralizan, de tal forma
que ningún cambio tiene lugar sin que las condiciones
sean anunciadas y conocidas y sin que los vendedores
tengan la oportunidad de rebajar sus precios y los compradores de aumentarlos. Así funcionan las bolsas de
valores públicos, las bolsas de comercio, los mercados de
grano, de carne, etc. ”
49

50. “Al lado de estos mercados existen otros donde la
competencia, aunque no tan bien organizada, funciona
todavía de una manera bastante adecuada y satisfactoria:
tales son los mercados de frutas y legumbres, de volatería.
Las calles de una ciudad donde se encuentran almacenes y
panaderías,
carnicerías,
tiendas
de
ultramarinos, sastrerías, zapaterías, constituyen
mercados con una organización un poco más defectuosa
desde el punto de vista de la competencia pero, sin
embargo, ésta se encuentra presente de forma suficiente.
(…)”
50

51. “Supondremos un mercado perfectamente organizado (*) desde el punto de vista de la competencia,
de igual forma que en la mecánica pura se supone que las máquinas se encuentran libres de rozamientos.”
(Walras, Elementos, 41)
(*) Quizás de aquí proviene el término “competencia perfecta”.
51

52. Diremos que un mercado funciona bajo competencia
perfecta si ningún agente, aisladamente, tiene
influencia significativa sobre los precios del mercado.
Para decirlo de manera coloquial, un agente
(consumidor o productor) dentro de un mercado
competitivo es lo que una gota dentro de una gran
piscina: hace parte de ella, pero si retiramos esa
gota, en nada afectará la cantidad de agua en la
piscina.
A un mercado así se le llama “mercado competitivo”
o “mercado bajo competencia perfecta”. Este
tipo de mercado es, en la práctica, un imaginario
teórico; una utopía. Pero, para la economía
neoclásica, una útil utopía.
52

53. Por su parte, si algún agente del mercado sí
tiene influencia sobre algún precio del mercado, entonces el mercado funciona bajo
competencia imperfecta (por ejemplo, monopolios, oligopolios, etc.).
53

54. EL ESTUDIO DE LA INSTITUCIÓN
DEL MERCADO, ES EL CORAZÓN DE LA TEORÍA NEOCLÁSICA.
54

55. EN
RESUMEN:
EN EL CURSO DE MICROECONOMÍA I, ESTUDIAREMOS EL COMPORTAMIENTO DEL
MERCADO A LA LUZ DE LA TEORÍA NEOCLÁSICA.
Y, PARA HACERLO, ESTUDIAREMOS
LAS
UNIDADES BÁSICAS (CONSUMIDORES Y
PRODUCTORES) EN INTERCAMBIO DE BIENES Y SERVICIOS, DENTRO DE LA INSTITUCIÓN DEL MERCADO A TRAVÉS DE LOS
PRECIOS.
55

56. LA INSTITUCIÓN DE MERCADO BAJO
COMPETENCIA PERFECTA CONSISTE EN:
1. UN CONJUNTO DE MERCANCÍAS (BIENES Y
SERVICIOS) QUE SON “ESCASAS”; ES
DECIR,
ESCASAS EN NÚMERO Y DESEADAS. Y TAMBIÉN QUE CADA MERCANCÍA ESTÁ DETERMINADA POR FECHA
Y LUGAR.
56

57. 2. UN MERCADO
ES UN LUGAR GEOGRÁFICO
(O VIRTUAL) EN DONDE LOS AGENTES (CONSUMIDORES Y PRODUCTORES) LLEVAN A
CABO LAS TRANSACCIONES DE LAS MERCANCÍAS. ESTA INSTITUCIÓN DEL MERCADO
SE CREA A TRAVÉS DE LOS DERECHOS
ADQUIRIDOS POR LOS AGENTES (INGRESO
EN LOS CONSUMIDORES Y TECNOLOGÍA EN
LOS PRODUCTORES).
57

58. 3. LOS
PRECIOS SON TOMADOS POR LOS AGENTES
(CONSUMIDORES Y PRODUCTORES) DEL MERCADO, DE MANERA PARAMÉTRICA. ES DECIR, EL
PRECIO ES UN DATO ARROJADO POR EL MERCADO
EN SU FUNCIONAMIENTO AGREGADO, PERO NO
ES DETERMINADO, DE MANERA UNILATERAL, POR
NINGÚN AGENTE DE LA ECONOMÍA.
(COMO HABÍAMOS DICHO ANTES, UN AGENTE
(CONSUMIDOR O PRODUCTOR) DENTRO DE UN
MERCADO COMPETITIVO ES LO QUE UNA GOTA
DENTRO DE UNA PISCINA: HACE PARTE DE ELLA,
PERO SI RETIRAMOS ESA GOTA, EN “NADA”
AFECTARÁ LA CANTIDAD DE AGUA EN LA
PISCINA).
58

59. 4. ESTOS PRECIOS ESTARÁN FORMADOS POR LA IGUALACIÓN DE LA
OFERTA Y LA DEMANDA DEL MERCADO.
59

60. Sin duda, la hipótesis de competencia
perfecta también tiene un criterio moralista:
¡ Todos son iguales ante el
mercado competitivo !
60

61. Tareas para la clase con el profesor
auxiliar
Presentar, de manera sencilla, la noción de
función de dos variables, y las nociones de
derivada parcial y de curva de nivel.
Tareas para la monitoría
Presentar, de manera sencilla, la noción de
derivada de una función de una sola variable, y el
criterio de primer orden para maximizar y
minimizar esa función.
61

62. Sugerencias
1. Hacerme preguntas en la clase magistral.
2. Escribirme al correo para preguntas y comentarios (smonsalveg@unal.edu.co).
3. Ir a la oficina (Cuarto piso, 5B, Edif. 311) en mi
horario de atención a estudiantes (Jueves, 11 a 1
pm), o pedirme cita por correo electrónico.
4. Asistir a las clases (en tablero) con los profesores
auxiliares que consideren conveniente. Ellos
presentan el mismo material, consistente en
ejercicios previamente asignados por el profesor
titular.
62

63. 5. Asistir a las monitorías (se avisarán próximamente los horarios).
6. Leer con antelación la clase magistral en diapositivas que les envío a su correo electrónico
oficial.
7. Traer las diapositivas (impresas o en su
computador personal) a la clase magistral y
sobre ella hacer las anotaciones que consideren pertinentes.
63

64. CLASE MAGISTRAL #2
-PRINCIPIOS DE LA TEORÍA DEL
CONSUMO
-MAXIMIZACIÓN DE LA UTILIDAD
Y MINIMIZACIÓN DEL GASTO
64

65. Un consumidor es una persona, un grupo o una familia con un propósito de consumo unificado.
La teoría neoclásica del consumo (o del consumidor)
bajo competencia perfecta, busca entender el proceso de la formación de la demanda bajo los parámetros
de la economía como ciencia natural; es decir, asumiendo a los consumidores como partículas, y optimizando cierta función para obtener las demandas.
65

66. Y el problema es: ¿cuál es esa función?
Para ello, la teoría neoclásica asume
que, de alguna forma, existe un “deseo
interno” del consumidor hacia las
mercancías, que lo lleva a demandar por
ellas.
Por
ejemplo, Walras (1909)
decía, de manera
parafra-seada, lo
siguiente:
66

67. Los
fenómenos
mecánicos
son
exteriores, pero los fenómenos económicos
(de la demanda) son interiores. Se tienen
instrumentos para determinar la atracción
de los astros los unos hacia los otros, pero
no se tienen para medir la intensidad de
las necesidades en las personas que intercambian. Pero no importa, puesto que cada
individuo que intercambia se encarga de
operar él mismo esta medida, consciente o
inconscientemente, y de decidirlo en interior profundo.
67

68. “Que la medida sea exterior o que sea interior,
en razón de que los hechos que se van a
medir sean físicos o psíquicos, no impide
que exista esta medida; es decir, que sea
posible la comparación cuantitativa.”
Se creyó, entonces, en la existencia de una
“función de utilidad” (cardinal u ordinal) que
medía, de manera comparada, ese deseo por
las mercancías.
68

69. Y agregaba Walras (también de manera para
fraseada):
“Así como las fuerzas serán causa del espacio
recorrido por un objeto, y las masas serán
causa del tiempo empleado en recorrer ese
espacio, las utilidades (y las “raretés” *)
serán la causa de la demanda.”
(*) “La “rareté” es la derivada de la utilidad efectiva respecto a la
cantidad poseída, exactamente como se define la velocidad: la
derivada de la distancia recorrida respecto al tiempo empleado en
recorrerla” (Walras, 1874)
69

70. En adelante trabajaremos, fundamentalmente,
con dos mercancías, x e y, aunque todo es posible
extenderlo, inmediatamente, a tres o más mercancías. Para nuestro enfoque, sin embargo, esto
es suficiente, pues será usual en este curso,
interpretar a x como la mercancía a estudiar, y a
y como el “resto de mercancías”.
En nuestro curso, una función de utilidad U(x , y)
mide, de alguna forma, la “satisfacción” que la canasta (x , y) le produce al consumidor.
70

71. GRÁFICA DE UNA FUNCIÓN DE UTILIDAD EN
DOS DIMENSIONES
z
z=U(x,y)
∙
y
∙(x,y)
x
71

72. 72

73. 73

74. A partir de la función de utilidad U(x,y), es muy
conveniente, desde el punto de vista gráfico,
calcularle sus correspondientes curvas de
nivel de utilidad (o curvas de isoutilidad):
U(x ,y ) = U0
donde U0 es una constante. Se trata de todas las canastas (x,y) que tienen el mismo
nivel de utilidad, es decir, que le producen al
consumidor la misma satisfacción.
74

75. z
Superficie z=U(x,y)
Plano z= U0
y
U(x,y)=U0
x
¿Cómo se forman las curvas de nivel?
75

76. Veamos un par de ejemplos:
i) U(x , y) = x y = U0 (curvas de nivel (o de indiferencia)). De donde, despejando, se obtiene que
y = U0 /x (hipérbolas)
y
U0 =4
U0 =3
U0 =2
U0 =1
E∙
B∙
A∙
C∙
A es menos preferido que
B y que C (es decir, A tiene
menos utilidad (U0 =1)). Por su
parte, B y C son indiferentes
(ambas tienen la misma utilidad
(U0 =2)). Etc.
D∙
x
76

77. Por ejemplo, si U0=1, la curva de nivel es la hipérbola y= 1/x.
77

78. ii) U( x, y) = √x + y = U0 (curvas de indiferencia).
De donde se obtiene que
y = U0 – √x
(parábolas)
y
•
y = 3- √x
U0 =3
U0 =2
y= 2- √x
•
x
78

79. HIPÓTESIS SOBRE LAS CURVAS DE NIVEL DE UTILIDAD
i) Primero, asumiremos que las curvas de nivel satisfacen
la condición de convexidad:
Las combinaciones convexas son
“mejores” que la especialización
(“hipótesis de la dieta balanceada”)
•x
λx + (1- λ)y,
•
0≤ λ ≤1
Combinaciones convexas
•
y
79

80. Otras condiciones que asumiremos son:
ii) Todo el espacio ℝ²₊₊ está cubierto por estas
curvas de nivel. A esta característica la llaman
“completez” de las curvas de indiferencia.
iii) Las curvas de indiferencia son “continuas”.
iv) Un aumento en las cantidades consumidas (de
la mercancía x o de la mercancía y) implica un
aumento de la utilidad. Por lo tanto, las curvas
“más lejanas” al origen son las que tienen
mayor nivel de utilidad. A esta característica la
llaman “monotonicidad” de las curvas de
indiferencia.
v) Las curvas de indiferencia son “transitivas”.
80

81. Completez, Continuidad , Monotonicidad y
Transitividad de las Curvas de Indiferencia
y
Crecimiento de las preferencias:
“más consumo, más satisfacción (utilidad)”
0
x
81

82. Ahora pasamos al segundo instrumento (después de la función
de utilidad) en la teoría del consumidor: la restricción
(o recta) presupuestal:
p₁ x + p₂ y = M
donde:
i) p₁ es el precio por unidad del bien x.
ii) p₂ es el precio por unidad del bien y.
iii) M es el presupuesto (renta) que tiene el consumidor
para gastar en las mercancías x e y. En principio, no
depende de los precios.
82

83. Recta presupuestal
y
Está compuesta por todas las canastas (x,y) que puede
adquirir un consumidor con presupuesto M, a los
precios de mercado p1 y p2.
M/p₂•
∙ (x,y)
p₁x + p₂y = M
(recta presupuestal)
•
M/p₁
x
83

84. Cambio de M en la restricción presupuestal
y
M’/p2
Recta presupuestal con aumento de M
M/p2 •
p₁ x + p₂ y=M
(recta inicial)
•
M/p1
M’/p₁
x
84

85. Cambio de p2 en la restricción presupuestal
Aumento en p2
y
M/p₂•
M/p’₂
Recta presupuestal con aumento de p2
p₁ x + p₂y=M
(recta inicial)
•
x
85

86. Cambio de p1 en restricción presupuestal
y
Recta presupuestal con aumento de p1
M/p2•
p₁ x + p₂ y=M
(recta inicial)
M/p’1
•
M/p₁
Aumento en p₁
x
86

87. Oportunidades de mercado perdidas y ganadas por
variación de parámetros
Recta presupuestal
Canastas ahora imposibles (en amarillo)
por el aumento del precio p1
p1 x + p2 y = M
Canastas ahora imposibles (en amarillo)
por disminución del presupuesto M
87

88. Uniendo las dos piezas claves en la teoría del
consumidor (función de utilidad y restricción
presupuestaria), llegamos al problema básico
de la teoría del consumo:
Maximizar
U(x, y)
sujeta a p₁ x + p₂ y = M
Es decir, maximizar la satisfacción en el
consumo, sujeta al presupuesto que se
tenga disponible y a los precios del
mercado.
88

89. MAXIMIZACIÓN DE LA UTILIDAD
y
U(x , y) = U(x*,y*)
y*
•
p₁ x + p₂ y = M
x*
x
89

90. EJEMPLO TÍPICO DE UN PROBLEMA DE
CONSUMIDOR
Maximizar
xy
sujeta a p₁ x + p₂ y = M
Solución
La restricción p₁ x + p₂ y = M la podemos
reducir a
y= (M - p₁ x)/ p₂
(*)
90

91. Y con esto, reducimos nuestro problema de optimización
a la siguiente forma
Maximizar
x(M- p₁ x )/ p₂
( = (Mx - p₁ x2 )/ p₂)
Derivando esta función con respecto a x, e igualando a cero,
obtenemos que
(M - 2 p₁ x) / p₂ = 0
y así
M - 2 p₁ x=0
o bien,
x = M / 2 p₁
91

92. y, reemplazando en (*) , llegamos a que
y = M / 2 p₂
Y así obtenemos las demandas marshallianas de este consumidor:
x * = M / 2 p₁
;
y* = M / 2 p₂
Noten que estas demandas son directamente proporcionales al presupuesto M, e inversamente proporcionales a su propio precio.
Y que, además, si el presupuesto y los precios se multiplican
por
la
misma cantidad (es decir, se duplican, se
triplican, etc.), las demandas marshallianas no cambian.
92

93. Y la utilidad máxima es:
U(x* , y*)= x* y* = (M / 2 p₁)( M / 2 p₂)
= M² / 4 p₁ p₂
A esta función se le conoce como la función
de utilidad indirecta de este consumidor.
Así,
V(M, p₁, p₂) = M² / 4 p₁ p₂
que es una función (de bienestar) estimable
econométricamente.
93

94. EL PROBLEMA DUAL DEL CONSUMIDOR:
MINIMIZACIÓN DEL GASTO
Paralelo al problema de maximizar la utilidad sujeta a la restricción presupuestaria, el
consumidor tiene otra alternativa: minimizar
el gasto del hogar. Como veremos, este problema tiene un carácter más normativo.
94

95. En lugar del problema básico del consumidor
Maximizar U(x, y)
sujeta a p₁ x + p₂ y = M
el problema de minimización de su gasto es:
Minimizar p₁ x + p₂ y
sujeta a U(x, y) = U₀
donde U₀ es un nivel de utilidad (bienestar)
fijo deseado.
95

96. MINIMIZACIÓN
DEL
GASTO
y
Curva de isocosto
p₁ x + p₂ y = e
Curva de nivel
U(x , y)= U₀
h₂
•
h₁
p₁ x + p₂ y = e (= p₁ h₁ + p₂ h₂)
x
96

97. Para calcular el gasto, no requerimos de llevar
a cabo nuevos cómputos: basta con tener
resuelto el problema central del consumidor.
Veamos cómo.
En el primer ejemplo, donde U(x , y) = x y,
teníamos que las demandas marshallianas eran
x*= M / 2p₁
y* = M / 2p₂
Y la utilidad máxima (o utilidad indirecta) era
U = M² / 4p₁p₂
97

98. En esta última ecuación
U = M² / 4 p₁ p₂
simplemente hacemos U=U₀ y M=e (esta e
proviene del inglés “expenditure” que significa
“gasto”), para obtener:
U₀ = e² / 4 p₁ p₂
y de allí se obtiene:
e = 2 (U₀ p₁ p₂)½
que es la función de gasto de este consumidor.
98

99. Esta función mide, exactamente, cuánto requiere “gastar” una familia para aumentar su
nivel de bienestar.
O de otra forma: ella permite medir en cuánto debe
compensarse a una familia para que recupere su
nivel de bienestar, ante, por ejemplo, un aumento
de precios.
Es muy utilizada en problemas de políticas públicas y
sociales debido a que es estimable econométricamente. Más adelante aclararé un poco más
este punto.
99

100. Ahora: A partir de la función de gasto
e= p₁ x + p₂ y
y derivando parcialmente, obtenemos las demandas
así:
∂e/∂p₁ = x
,
∂e/∂p₂ = y
Pero en este momento, estas demandas cambian de
notación y de nombre: se llaman demandas hicksianas (o demandas compensadas) ( John Hicks (1939))
y satisfacen entonces las ecuaciones:
100

101. ∂e/∂p₁ = h₁
,
∂e/∂p₂ = h₂
(Lema de Shephard)
donde
h₁ = la demanda hicksiana por el bien x
h₂ = la demanda hicksiana por el bien y
Estas ecuaciones muestran que si estimamos econométricamente la función de gasto (lo cual es posible mediante la
Encuesta Nacional de Hogares (DANE)), también podremos
estimar las demandas hicksianas.
101

102. En el caso del ejemplo que venimos discutiendo,
teníamos que:
e = 2 (U₀ p₁ p₂)½
Y, por lo tanto, por el teorema de Shephard,
h₁ = ∂e/∂p₁ = U₀ p₂(U₀ p₁ p₂)-½
h₂ = ∂e/∂p₂ = U₀ p₁(U₀ p₁ p₂)-½
lo que nos lleva, simplificando, a que las demandas
hicksianas de este consumidor son:
h₁ = (U₀ p₂/ p₁)½
h₂ = (U₀ p₁/ p₂)½
102

103. ¿Pero qué es lo que miden las demandas hicksianas?
(h1(p1, p2, U0), h2(p1, p2, U0))
M/p2
M/p’2
∆e
•A
(h1(p1, p’2, U0), h2(p1, p’2, U0))
•B
U(x, y)=U0
M/p1
103

104. Estando en el punto A, sucede un aumento en el precio
p2, y así pasamos de la recta presupuestaria
azul a la morada. Para recuperar el nivel de bienestar
U0, debemos entonces aumentar el gasto en ∆e
(presupuesto) y, al hacerlo, pasamos a la recta presupuestaria amarilla (que es paralela a la morada), y
llegamos al punto B.
En el gráfico, señalamos las correspondientes demandas hicksianas en los puntos A y B, y el gasto (∆e)
necesario para regresar al nivel U0. Las demandas
hicksianas, entonces, miden los cambios del punto A
de consumo al punto B de consumo (debido a un
aumento en el precio p2), pero sin abandonar el nivel de
bienestar U0 .
104

105. EJEMPLO BÁSICO
Maximizar
sujeta a
U(x,y) = x y
3x+2y=45
Si el precio de x aumenta en un 20%, calcule las
demandas hicksianas y el gasto.
Solución
Las demandas marshallianas de este problema son:
x*= (45)/(2)(3)= 7.5 ,
y*= (45)/(2)(2)= 11.25
Y el nivel de utilidad recibido allí es:
U(x*,y*) = (7.5) (11.25) = 84.375
105

106. Si aumenta el precio del bien x en 20%, las nuevas
demandas marshallianas son:
x**= (45)/(2)(3,6) = 6.25
;
y**= (45)/(2)(2) = 11.25
El nivel de utilidad ha bajado a
U(x**, y**) = (6.25) (11.25) = 70.3125
Para regresar al nivel de utilidad original de 84.375,
debemos aumentar el presupuesto; es decir, debemos
“invertir” en el hogar una cantidad que está dada, precisamente, por la función de gasto ya calculada:
e = 2 (U₀ p₁ p₂)½ = 2[(84.375)(3.6)(2) ] ½ = 49.295
106

107. La nueva recta presupuestal es, entonces,
3.6x + 2y = 49.295
que es paralela a la segunda recta presupuestal
3.6x + 2y = 45.
Y las nuevas demandas serán:
h1 = (49.295 )/( 2)(3.6) = 6.8465
h2 = (49.295 )/(2)(2) = 12.3237
Notemos que
U(h1 , h2) = U(6.8465 , 12.3237) = 84.375
es el nivel de utilidad original.
107

108. Ejercicios para la clase en tablero con el
profesor auxiliar (Mabel ó Salomón)
1) A partir de la restricción presupuestal 5x+ 10y=36,
estudie las oportunidades de mercado perdidas y
ganadas por variación de parámetros, si:
i) El precio p=10 cambia a p=9.
ii) El precio p=5 cambia a p=10.
iii) El presupuesto cambia de M=36 a M=16.
iv) Se establece un racionamiento hasta x*=1.
v) Se establece un impuesto de $0.5 a cantidades
superiores a x*=2.
108

109. 2) Una compañía telefónica ofrece unas tarifas
especiales opcionales para las llamadas
nacionales, según las cuales los primeros 50
minutos mensuales son gratuitos, los 100
siguientes cuestan $0,25 el minuto, y el resto se
rige por la tarifa normal de $0,50 el minuto. Trace
la restricción presupuestaria de un usuario que
tiene un ingreso de $400 al mes, entre llamadas
regionales y un bien compuesto (“lo demás” que
consume el usuario).
3) Discutir con ejemplos sencillos (por ejemplo,
con el ejercicio 1) anterior)
ceteris paribus.
la noción de
109

110. 4) Un consumidor tiene una función de utilidad U(x , y) =6x + y,
con restricción presupuestal 5x+2y=45. Recurriendo a
una buena gráfica, responda lo siguiente:
i) ¿Cuál de los dos bienes le gusta más a este consumidor?
ii) ¿Cuáles son sus demandas?
iii) ¿Qué nivel de utilidad (bienestar) máxima alcanza?
5) Calcular las demandas marshallianas, la función de
utilidad indirecta, la función de gasto y las demandas
hicksianas en los siguientes casos, generando una tabla
con estos datos:
i) U(x , y)= xα yβ ( Función Cobb-Douglas)
ii) U( x ,y ) = Min {x , y} (Función Leontief)
110

111. 6) Comprobar la identidad de Roy
x= - ∂v/ ∂p₁ / ∂v/ ∂M
; y= - ∂v/ ∂p2 / ∂v/ ∂M
en el caso de las funciones Cobb-Douglas y Leontief.
Esta identidad permite recuperar las demandas marshallianas a partir de la función de utilidad indirecta.
7) A partir de la función de gasto
e = 2(√p₁√p₂) U₀
deduzca que la función de utilidad de la que se originó
es la Cobb-Douglas
U= √x √y
111

112. [Sugerencia: Muestre que
∂e/∂p₁= (√p₂ / √ p₁)U₀
∂e/∂p2 = (√ p₁ / √p₂) U₀
y como ∂e/∂p₁=x ,
∂e/∂p2=y entonces
(√p₂ / √ p₁)U₀ = x ,
(√ p₁ / √p₂)U₀ = y
Y así, multiplicando término a término estas ecuaciones,
se obtiene que
x y = (U₀)²
Y, por lo tanto,
U₀ = √x √ y
que es una función Cobb-Douglas con α = ½ y β = ½ .]
112

113. 8) (Explicarlo con videobeam si lo consideran adecuado)
En el problema
Maximizar
sujeta a
x 2y
3x + 2y = 45
si el precio de x aumenta en un 20%, calcule las
demandas hicksianas y el gasto.
Solución
Las demandas marshallianas de este problema son:
x*= 2(45)/( 3)(3)= 10 , y*= (45)/(3)(2)= 7.5
Y el nivel de utilidad recibido allí es:
U(x*,y*) = (10)2 (7.5) =750
113

114. Estas son también las primeras demandas hicksianas; es
decir:
h1(3, 2, 750) = 10 ,
h2(3, 2, 750) = 7.5
Si aumenta el precio del bien x en 20%, las nuevas
demandas marshallianas son:
x**= 2(45)/( 3)(3.6) = 8.33
;
y**= (45)/(3)(2) = 7.5
Para regresar al nivel de utilidad original, recurrimos a la
recta presupuestal 3.6x+2y=50.816 (que es paralela a la
segunda recta presupuestal 3.6x+2y = 45).
114

115. Y las nuevas demandas serán:
x*** = 2(50.816)/( 3)(3.6)= 9.41
y*** = (50.816)/(3)(2)= 8.47
Notemos que U(x***,y***) = U(9.41,8.47) = 750. Por lo
tanto,
h1(3.6, 2, 750) = 9.41 , h2(3.6, 2, 750) = 8.47
¿Y cómo calculamos el presupuesto 50.816 de arriba?
Es, precisamente, e(3.6, 2, 750), y se obtiene de
Minimizar e = 3.6x+2y
sujeta a
x2y=750
115

116. Ilustración del problema
45 / 2
Presupuesto inicial
3x + 2y = 45
3.6x + 2y = 50.816
8.47
7.5
∙
∙ ∙
8.33 9.41 10
3.6x + 2y = 45
45 / 3.6
45 / 3
116

117. 9) (Explicar con videobeam, si lo consideran adecuado)
OTRO EJEMPLO TÍPICO DE UN PROBLEMA
DE
CONSUMIDOR
Maximizar √x + y
sujeta a p₁ x + p₂ y = M
Este problema se reduce a:
Maximizar
√x + (M - p₁ x )/ p₂
Y derivando esta función con respecto a x, e igualando
a cero, obtenemos que:
117

118. (1 / 2√x) - (p₁ / p₂) = 0
de donde se obtiene que:
√x = p₂ / 2p₁
Y así,
x* = (p₂/ 2p₁)²
Y por lo tanto,
y* = (M - p₁ x)/ p₂
= (M- p₁ (p₂/ 2p₁)² )/ p₂
= (M/ p₂) – (p₂/4p₁)
118

119. Así, resumiendo, las demandas marshallianas
de este consumidor son:
x* = (p₂/ 2p₁)²
y* = (M/ p₂) – (p₂/ 4p₁)
Nótese que estas demandas dependen del
presupuesto (M) y de ambos precios (esto no
sucedió en el ejemplo anterior) ; y que, además,
si tanto el presupuesto como los precios
aumentan o dismi-nuyen de manera proporcional
(es decir, todos se duplican, se triplican, etc.),
entonces las
demandas marshallianas
son
exactamente las mismas.
119

120. y
Solución: x* = (p₂/ 2p₁)² ;
y* = (M/ p₂) – (p₂/ 4p₁)
p1x+p2y = M
•
∙
Para bajos presupuestos no existe demanda de y
x
120

121. Y la utilidad máxima es
U = √x + y = (p₂/ 2p₁) + [(M/ p₂) – (p₂/ 4p₁)]
= (M/ p₂) + (p₂/ 4p₁)
que es la función de utilidad indirecta
de este consumidor; es decir,
V(M, p₁, p₂) = (M/ p₂) + (p₂/4p₁)
121

122. Y la función de gasto se construye haciendo V=U0 y
M=e en la función de utilidad indirecta
V(M, p₁, p₂) = (M/ p₂) + (p₂/4p₁)
para obtener que:
U0 = (e/ p₂) + (p₂/4p₁)
Es decir,
e = U0 p₂ - ((p2)2/4p₁)
¿Cuáles son las demandas hicksianas?
122

123. 10) Utilidad cardinal y ordinal. Existen dos formas
de aproximación a la teoría de la elección racional de un consumidor: la cardinal y la ordinal.
Nosotros hemos estudiado la aproximación
cardinal mediante la función de utilidad.
Pero, desde aquí, pasar a la aproximación ordinal
es inmediato:
Se dice que una canasta (x, y) es preferida (o más
deseada) a (x’, y’), y lo escribiremos
(x , y) ≻ (x , y’)
si, y sólo si, U(x , y) > U(x’ , y’)
123

124. Y similarmente, diremos que (x,y) es preferida o
indiferente a (x’ , y’), y lo escribiremos
(x, y) ≽ (x’, y’),
si, y sólo si
U(x, y) ≥ U(x’, y’)
Y también se dice que (x, y) es indiferente a (x’,y’),
y escribiremos
(x, y) ∼ (x’, y’),
si, y sólo si,
U(x, y) = U(x’, y’)
124

125. EJERCICIOS
1)
COMPLEMENTARIOS PARA EL
ESTUDIANTE
Mabel consumía 100 unidades de X y 50
unidades de Y. El precio de X aumentó de 2
a 3. El precio de Y permaneció en 4. ¿En
cuánto tendría que aumentar la renta de
Mabel para que pueda permitirse el
continuar adquiriendo exactamente 100
unidades de X y 50 unidades de Y?
125

126. 2)
Salomón tiene como función de utilidad U(xA, xB) = xAxB
para los albaricoques (A) y los bananos (B). Supongamos que
el precio de los albaricoques es 1, el precio de las bananas es 2
y su presupuesto es 40.
(a) En un gráfico, trace la recta presupuestaria de Salomón.
Indique algunos puntos de su curva de indiferencia que
correspondan a un nivel de utilidad de 150. Ahora indique
algunos puntos de la curva de indiferencia correspondientes a
un nivel de utilidad de 300 y dibuje esta curva también.
(b) ¿Puede adquirir Salomón alguna cesta que le permita obtener
una utilidad de 150?
(c) ¿Puede adquirir alguna cesta que le permita obtener una
utilidad de 300?
(d) Indique en el gráfico una cesta que Salomón pueda adquirir y
que corresponda a una utilidad superior a 150?
126

127. 3)
Suponga que la ecuación presupuestaria es p1x + p2y = M. El
Gobierno decide establecer un impuesto de suma fija t al bien x,
y un subsidio de suma fija al bien y de s. Expresar algebraica y
gráficamente la nueva restricción presupuestaria.
4) a) A Jorge Luis le gusta el pan pero es indiferente ante el queso
(bien neutral). Muestre que las curvas de indiferencia son verticales
si en el eje x se colocan las cantidades de pan y, en el eje y, el queso.
b) ¿Podría dibujar curvas de indiferencia que describan el
comportamiento de un consumidor que se sacia con 10 tazas de
agua y 10 cucharaditas de café instantáneo?
c) Julián es un tipo al que le gusta mucho el whisky, pero que
aborrece el agua. Hasta tal punto es así, que solo está dispuesto a
beberse un vaso de agua si le dan también un vaso de whisky.
¿Podría mostrar una función de utilidad que describiera las
preferencias de Julián respecto a los vasos de agua y de whisky?
127

128. 5) Calcular las demandas marshallianas, la función
de utilidad indirecta, la función de gasto y las
demandas hicksianas en los siguientes casos,
generando una tabla con estos datos:
i) U(x , y)= √x + y (Función separable)
ii) U( x ,y ) = ln(1+x) + y (Función separable)
iii) U( x ,y ) = Min {7x ,5 y} +1 (Otra función tipo Leontief)
128

129. 6) (Carrasco, et al.)
Dora, Martha, Esperanza, Elena y Marcela son cinco
funcionarias de la Universidad que acostumbran a comer en el
comedor de la Facultad. El menú está compuesto por platos de
verdura y platos de carne. Las preferencias de las cinco funcionarias
entre verdura (bien x) y carne (bien y), son diferentes. Así, Dora debe
seguir una dieta rigurosa y tiene que comer tanto carne como verdura,
pero siempre en una proporción del triple de verdura que de carne. A
Martha le gusta tanto el carne como la verdura, pero prefiere no
consumir juntos los dos tipos de alimentos. Esperanza, por su parte,
estaría siempre dispuesta a intercambiar un plato de carne por dos de
verduras, aunque ambos alimentos le agradan. A Elena, sin embargo,
no le gusta el carne, aunque sí la verdura, y sólo está dispuesta a
comer algo de carne si a cambio recibe una dosis extra de verdura. Por
último, a Marcela le gusta el carne, mientras que la verdura le es
indiferente. No le importa comerla, pero ello no le reporta ninguna
satisfacción. Para cada una de las funcionarias, caracterice sus
preferencias y defina una función de utilidad (curvas de indiferencia)
que las represente.
129

130. 7) Consideremos un consumidor cuyas preferencias se representan mediante la función de
utilidad
U(x,y) = Min {y+2x, x + 2y}
a) Deduzca las demandas marshallianas.
b) Represente gráficamente la curva de indiferencia correspondiente al nivel de utilidad
U=20.
8) ¿Es la cocaína un “bien” para el consumidor en
el sentido que se estudia en este curso, aún
sabiendo que puede ser dañina al consumidor?
Explique.
130

131. y
9)
M/p’2∙
Confirmar o negar el comportamiento de las
demandas
marshallianas del consumidor con U(x,y)=xy
∙B
M/p2 ∙
A∙
C
∙
∙
M/p1
∙
M/p’ 1
x
131

132. CLASE MAGISTRAL #3
TIPOS DE MERCANCÍAS Y LA
NOCIÓN DE ELASTICIDAD
132

133. ANÁLISIS GENERAL DEL
PROBLEMA DEL CONSUMIDOR
Recobrando inicialmente el problema central del
consumidor:
Maximizar U(x, y)
sujeta a p₁ x + p₂ y = M
ahora lo resolvemos en forma general recurriendo
al método de los multiplicadores de Lagrange.
133

134. Escribimos el lagrangiano
L = U(x, y) + λ(M - p₁ x - p₂ y )
Y derivamos con respecto a x, y, λ:
∂L /∂x = ∂U/∂x - λ p₁ = 0
∂L /∂y = ∂U/∂y - λ p₂ = 0
∂L /∂ λ = M - p₁ x - p₂ y = 0
Lo que nos lleva a las ecuaciones de equilibrio del
consumidor:
(∂U/∂x)/ (∂U/∂y) = p₁/ p₂ ;
p₁ x + p₂ y = M
134

135. Al término
(∂U/∂x) / (∂U/∂y)
se le llama “tasa marginal de sustitución entre las
mercancías x e y”. Y, por lo tanto, la ecuación de
equilibrio
(∂U/∂x)/ (∂U/∂y) = p₁/ p₂
Ecuación de equilibrio (de Jevons)
que se conoce como ecuación de Jevons, se lee:
“tasa marginal de sustitución igual a la relación de
precios”
135

136. Pero…¿qué mide la tasa marginal de sustitución?
Veamos.
La curva de nivel que pasa por el punto de
equilibrio del consumidor (es decir, que pasa por
las demandas marshallianas (x*,y*)), satisface
la ecuación
U(x , y) = U(x*,y*)
siendo U(x*,y*) =U0 una constante.
136

137. Tomando entonces derivadas parciales a ambos lados de la
ecuación U(x , y) = U0 se obtiene que
(∂U/∂x) dx + (∂U/∂y) dy = 0
ó
(∂U/∂x) dx = - (∂U/∂y) dy
Y, de allí, obtenemos que:
(∂U/∂x) / (∂U/∂y) = - d y / d x
Es decir, las tasas marginales de sustitución coinciden con las pendientes de las rectas tangentes a las
curvas de nivel.
137

138. y
U(x,y)=U0
(∂U/∂x) / (∂U/∂y) ≈
1
x
Así, la tasa marginal de sustitución mide la cantidad que debe aumentarse de y al disminuir “una
unidad” de x, pero siempre manteniéndose en la
misma curva de utilidad.
138

139. Lo importante aquí, es que, en equilibrio,
esta tasa marginal de sustitución es,
exactamente, la relación de precios p₁/p₂
dada por el mercado.
139

140. y
En la asignación A puedo ir al mercado y cambiarla
(a los precios corrientes) por la asignación B que me
da más utilidad, etc. Hasta llegar al punto E.
-∂U/∂x / ∂U/∂y
= Pendiente de la
curva de nivel
A∙
B∙
C∙
E
•
F
•
Pendiente de la recta = -p1/p2
x
A este tipo de procesos, Marshall (1920) los reunía bajo el rótulo de “Principio de
sustitución”.
140

141. Por lo tanto, esta ecuación de equilibrio (que
algunos autores la asimilan, para el consumo,
con una “ecuación de calor”, o de “ecuación
termodinámica”) es una igualdad entre una
tasa subjetiva de intercambio con una tasa
real de intercambio en el mercado. Es decir,
es la igualdad entre un “costo de oportunidad
subjetivo” (del consumidor) con un “costo de
oportunidad objetivo” (mercado).
141

142. O en otras palabras:
La tasa marginal de sustitución nos dice cuánto
vale el bien 1 en términos del bien 2 para el
consumidor (tasa subjetiva), mientras que el
precio relativo nos dice cuánto vale el bien 1 en
términos del bien 2 para el mercado (tasa
objetiva).
142

143. Ejemplo
Para resolver
Maximizar xαyβ
sujeta a p1x+ p2y=M
escribimos directamente la ecuación “tasa
marginal de sustitución = relación de precios”:
(∂U/∂x)/ (∂U/∂y) = p₁/ p₂
(Ecuación de equilibrio (de Jevons) )
que en este caso es:
143

144. α xα-1 yβ / β xα yβ-1 = p₁/ p₂
de donde obtenemos, cancelando términos, que
αy/βx = p1/p2
y así,
y = βp1x/αp2
Ahora colocamos esta ecuación en la restricción
presupuestaria p1x+p2y=M, y obtenemos
p1x + p2 (βp1x/αp2) = M
Y despejando x, se llega a que:
144

145. x* = αM/(α+β)p1
Y llevando esto a la restricción presupuestal
y despejando y, obtenemos que
y* = βM/ (α+β)p2
Con ello hemos encontrado las demandas
marshallianas utilizando la ecuación de Jevons.
145

146. COMPORTAMIENTO GENERAL DE LAS
DEMANDAS DE LA FUNCIÓN COBBDOUGLAS
aumenta p2
M/p2
•A
M/p´2
•B
•B
•
A
M/p1
M/p´ 1
disminuye p1
146

147. Un ejemplo importante
Consideremos el caso de la “función cuasilineal”
(donde U(.,.) es una función cóncava estricta)
U(x , y) = U(x) + y
Este tipo de función de utilidad es importante porque
concentra su atención en el comportamiento de la
mercancía x, dejando la variable y (ye) para el “resto”
del consumo.
Escribiendo la ecuación de equilibrio para este caso,
obtenemos que
U’(x) / 1 = p₁/p₂
ó
U’(x) = p₁/p₂
147

148. Si se asume p₂=1 (numerario), entonces se llega a que
U’(x)
=
p₁
(Utilidad marginal = precio)
Ecuación de equilibrio del consumidor
Es decir, para maximizar la utilidad, un hogar consume
una cantidad x, de tal forma que su utilidad marginal
sea igual al precio del mercado. En otras palabras,
consume hasta que al agregar una unidad más, la
diferencia de utilidades coincide con el precio del
mercado. Esta utilidad marginal era lo que Walras
llamaba “rareté”.
148

149. Decisión de consumo de un hogar que solo
demanda un bien
U(x)
Pendiente U´(x*)
•
p₁
1
x*
Función cóncava:
utilidad marginal
decreciente como
típica hipótesis
neoclásica
x
149

150. U(x)
Precio más bajo
Precio más alto
∙
p1
1
∙
X*
x**
x
Note que si p1 crece, entonces, dada la concavidad estricta de la
función de utilidad, la cantidad consumida x, disminuye.
En su momento histórico se consideró, por parte de algunos
economistas, como un descubrimiento de primer nivel científico.
Es corriente utilizar esta condición como la ecuación de equilibrio
en el caso de los hogares que consumen un bien (digamos
“canasta familiar”) con un IPC (Índice de Precios al Consumidor)
dado por el DANE.
150

151. Algunas Críticas al Modelo
Neoclásico del Consumidor
Existencia misma de la función de utilidad.
ii) Racionalidad del consumidor; es
decir, comportamiento optimizador de
este agente económico.
iii) Gustos estáticos: puede haber cambios en
los gustos.
iv) Los precios pueden influir en los gustos:
interacción gustos-precios.
i)
151

152. Metodología General de la
Economía Neoclásica
i)
PLANTEAR EL PROBLEMA DEL AGENTE
OPTIMIZADOR.
ii) ENCONTRAR LOS EQUILIBRIOS DEL
AGENTE OPTIMIZADOR.
iii) HACER ESTÁTICA COMPARATIVA SOBRE
LOS EQUILIBRIOS (ceteris paribus).
152

153. ESTÁTICA COMPARATIVA CON LAS
DEMANDAS MARSHALLIANAS
En nuestro caso del consumidor, ya tenemos el
problema principal, y ahora haremos estática
comparativa con las demandas marshallianas.
Primer Caso. ¿Qué sucede con las demandas
marshallianas si M varía pero los precios
están fijos?
Segundo Caso. ¿Qué sucede con las demandas
marshallianas si los precios varían pero M
queda fijo?
153

154. Análisis parcial del primer caso: Precios fijos y
presupuesto variante
En esta situación tendremos dos posibilidades:
a) ∂x/∂M > 0 : es decir, cuando al aumentar
M, también aumenta la demanda del bien x.
En este caso, diremos que x es un bien normal.
Lo mismo si ∂y/∂M > 0.
b) ∂x/∂M < 0: es decir, cuando al aumentar
M, disminuye la demanda del bien x. En este
caso, diremos que x es un bien inferior.
Lo mismo si ∂y/∂M < 0.
154

155. y
•C
En C, x es un bien
inferior pero y es
un bien normal
•B
En B, ambos
bienes (x e y) son
normales
A•
•D
En D, x es un bien
normal pero y es
inferior
x
155

156. Análisis parcial del segundo caso: Presupuesto
fijo y precios variantes
En esta situación tendremos dos posibilidades típicas:
a) ∂x/∂p₂ > 0, ∂y/∂p₁ > 0 : es decir, cuando al
aumentar p₂, aumenta la demanda del bien x; y
cuando al aumentar p₁, aumenta la demanda del
bien y. En este caso, diremos que x e y son bienes
sustitutos (brutos).
b) ∂x/∂p₂ < 0, ∂y/∂p₁ < 0 : es decir, cuando al aumentar
p₂, disminuye la demanda del bien x; y cuando al
aumentar p₁, disminuye la demanda del bien y.
En este caso, diremos que x e y son bienes
complementarios (brutos).
156

157. y
x e y son bienes
sustitutos brutos
M/p₂ •
•B
p₂’ >p₂
•A
M/p₂’•
•
C
•
M/p₁’
•
p₁’ > p₁
M/p₁
x
157

158. y
M/p₂ •
p₂’> p₂
M/p₂’
•
•A
B
•
x e y son bienes
complementarios
brutos
C •
•
•
M/p’₁
M/p₁
p’₁ > p₁
x
158

159. Ejemplos
La función Cobb-Douglas
U(x , y) = xα yβ
tiene como demandas marshallianas
x= αM/(α+β)p₁ ,
y = βM/ /(α+β)p₂
Y puesto que
∂x/∂M= α/(α+β)p₁ > 0 , ∂y/∂M= = β/ /(α+β)p₂ > 0
Entonces ambos, x e y, son bienes normales.
Sin embargo, puesto que ∂x/∂p₂ =0 y ∂x/∂p₁ =0, estos
bienes no son sustitutos ni complementarios brutos.
1.
159

160. Nota. Esto ha dado origen a que se estudie más
detenidamente este problema. Por ello, en lugar de
estudiar bienes sustitutos y complementarios con
las demandas marshallianas (x, y), se hace con
las demandas hicksianas (h1,h2) (es decir, sobre la
misma curva de utilidad). En tal caso, los bienes
se llamarán sustitutos y complementarios netos,
en lugar de sustitutos y complementarios brutos,
que son los que hemos definido anteriormente.
160

161. 2. La función de utilidad Leontief
U(x , y ) = Min {x , y }
tiene como demandas marshallianas
x* = M/(p₁+p₂) = y*
y
y=x
•
x*=y*= M/(p1+p2)
x
161

162. Y puesto que
∂x/∂M= 1/(p₁+p₂) > 0 , ∂y/∂M= 1/(p₁+p₂) > 0
entonces ambos, x e y, son bienes normales.
Además, puesto que
∂x/∂p₂ =-M/(p₁+p₂)² <0
∂y/∂p₁ = -M/(p₁+p₂)² <0
estos son bienes complementarios brutos.
¿Serán bienes complementarios netos?
162

163. LA NOCIÓN DE ELASTICIDAD
Continuando con el análisis de estática comparativa
con
las
demandas
marshallianas, ahora introducimos la noción
de elasticidad.
Ya estudiamos una clasificación de los bienes
(normal, inferior, complementario o sustituto)
de acuerdo al signo (positivo o negativo) de
las derivadas de las demandas marshallianas
(con respecto al ingreso y al precio).
163

164. Lo que ahora estudiaremos es exactamente cuánto es esa variación mediante porcentajes, es decir, mediante la
noción de elasticidad de la demanda:
“La elasticidad de la demanda en un mercado es
mayor o menor dependiendo de si la cantidad
demandada aumenta mucho o poco ante una
caida en el precio, y disminuye mucho o poco
para un aumento dado en el precio”.
(Marshall (1920))
164

165. En general, la elasticidad de una variable a con
respecto a otra variable b, es la siguiente:
Є=
= (variación porcentual de a) / (variación porcentual de b)
= (∆a/a) / (∆b/b)
O bien,
Є = (∆a/∆b) / (a/b) = (∆a/∆b) (b/a)
Y que, en el caso diferenciable, se escribe como
Є = (∂a/∂b) / (a/b) = (∂a/∂b)(b/a)
165

166. En nuestro caso, en que estamos haciendo estática comparativa
con las demandas marshallianas, distinguiremos dos tipos de
elasticidades:
1. Elasticidades-ingreso (o renta) de la demanda:
(∂x/∂M) / (x/M)
;
(∂y/∂M) / (y/M)
2. Elasticidades-precio de la demanda:
(∂x/∂p1) / (x/p1)
(∂x/∂p₂) / (x/p₂)
;
;
(∂y/∂p₂) / (y/p₂)
(∂y/∂p1) / (y/p1)
A estas dos últimas elasticidades se les llama “elasticidades- precio
cruzadas”. A las dos primeras, en ocasiones, se les llama “elasticidades del
propio precio”.
166

167. CLASIFICACIÓN DE LAS ELASTICIDADES
1. Si la elasticidad (precio o ingreso) es cero, diremos que
2.
3.
4.
5.
la demanda es perfectamente inelástica.
Si la elasticidad (precio o ingreso) es mayor que 1 en
valor absoluto, diremos que la demanda es elástica.
Si la elasticidad (precio o ingreso) es menor que 1 en
valor absoluto, diremos que la demanda es inelástica.
Si la elasticidad (precio o ingreso) es igual a 1 en valor
absoluto , diremos que la demanda tiene elasticidad
unitaria.
Si la elasticidad (precio o ingreso) es infinita en valor
absoluto, diremos que la demanda es perfectamente
elástica.
167

168. Determinar la elasticidad de la demanda es de gran
importancia para el sector empresarial y también para el
Estado, puesto que permite anticipar el comportamiento
del mercado ante una variación de factores como el precio
de los bienes y servicios.
Por ejemplo, con el incremento del precio de los combustibles,
es posible que el precio de muchos productos se
incremente también, por lo que es necesario que las
empresas puedan medir con exactitud cuánto afectará a
sus ventas esa situación y así realizar los ajustes y
correcciones necesarios para evitar el menor impacto
negativo posible.
Para una empresa de turismo por ejemplo, si se incrementa el
precio de los combustibles se incrementará el precio de los
pasajes, situación que posiblemente hará que muchas
personas decidan no ir de vacaciones, lo cual afectará
directamente a las empresas relacionadas con el turismo.
168

169. En los siguientes ejemplos, asumiremos que, de
manera
agregada,
o,
más
específicamente, sumando las demandas
individuales, logramos conseguir la demanda
agregada de un país o de un sector económico, y
que, mediante encuestas cuidadosamente
realizadas y análisis econo-métricos, se consigue
estimar estas elasticida-des. Cabe advertir
que, en muchas ocasiones, las agencias del
gobierno (DNP, DANE, etc.) son resistentes a
hacer públicos algunos de estos datos, por
razones que entenderemos un poco más
adelante.
169

170. ELASTICIDAD-RENTA DE LA DEMANDA DE CIERTO PAÍS
170

171. ELASTICIDAD-PRECIO DE LA DEMANDA DE CIERTO PAÍS
171

172. Ejemplo
Se estima que la demanda de petróleo tiene una elasticidadprecio de 0.05. Si el precio inicial del petróleo fuera US$108
el barril, y las cantidades iniciales de petróleo producidas
fueran de 50 millones de barriles, ¿cómo afectaría al precio
y a la cantidad de petróleo un embargo que redujera la
oferta mundial de petróleo en un 5 %?
Solución
Hay una reducción del 5% de la producción a 47.5 millones de
barriles, y, por lo tanto, habrá un alza en el precio por barril.
Pero como la elasticidad es de 0.05 y la reducción en la
producción fue del 5% entonces el precio tendrá que variar
100% (porque, por definición de elasticidad, a un 1% de
cambio en el precio le corresponde un 0.05% de cambio en
la producción; y el cambio que ocurrió fue del 5%, es decir,
100 veces 0.05). Por todo lo anterior, el nuevo precio, al
variar 100%, será de 216 dólares por barril.
172

173. Cuadro comparativo de elasticidades-precio de la demanda
Precio
•
1%
Elasticidad cero
Elasticidad infinita
•
1%
Curva de demanda más elástica
Curva de demanda menos elástica
•
X*
Demanda
173

174. Cuadro comparativo de elasticidades-ingreso de la demanda
para un bien normal
Ingreso
Demanda menos elástica
1%
Demanda con
elasticidadingreso cero
Demanda más elástica
1%
Demanda con elasticidad-ingreso infinita
Demanda
174

175. ¡¡Note que estas últimas elasticidades pueden depender del nivel
de precios vigente en el mercado, y así, las curvas de
demanda podrían tener una elasticidad diferente en cada
estado precio-demanda de la economía!! Por ello es que se
recurren a conceptos como “elasticidades de corto plazo” y
“elasticidades de largo plazo”.
Por lo tanto, debemos ser muy cuidadosos al momento de hacer
inferencias con resultados de elasticidades de demandas
agregadas: debemos entender si éstas son de corto o largo
plazo.
Aún así, las elasticidades son una herramienta de análisis muy
recurrida en el diseño de políticas macroeconómicas y microeconómicas.
175

176. Ejercicios para la clase en tablero con el
profesor auxiliar (Mabel ó Salomón)
1) CÁLCULO
TEÓRICO DE ELASTICIDADES
a) En
el caso de las demandas marshallianas
de las funciones Cobb-Douglas
x= αM/(α+β)p₁ , y = βM/ /(α+β)p₂
tenemos que sus elasticidades-ingreso
son unitarias:
(∂x/∂M) / (x/M) = (α/(α+β)p₁) / (αM/(α+β)p₁)/M = 1
(∂y/∂M) / (y/M) = (β /(α+β)p₂) / (βM/(α+β)p₂)/M = 1
176

177. b) Pero también las elasticidades-precio (propias)
de la demanda son unitarias:
•
(∂x/∂p₁) / (x/p₁) =
-(αM/(α+β)(p₁)²) / (αM/(α+β)p₁)/p₁ = - 1
•
(∂y/∂p₂) / (y/p₂) =
-(βM /(α+β)(p₂)²) / (βM/(α+β)p₂)/p₂ = - 1
Y las elasticidades cruzadas son cero:
•
(∂x/∂p₂) / (x/p₂) = 0 ;
(∂y/∂p₁) / (y/p₁) = 0
177

178. c) En el caso de las demandas marshallianas de
la función Leontief
x = M/(p₁+p₂) = y
tenemos que sus elasticidades-ingreso también
tienen elasticidad unitaria:
(∂x/∂M) / (x/M)
=(1/(p₁+p₂)) / (M/(p₁+ p₂)/M
= 1
= (∂y/∂M) / (y/M)
178

179. d)
•
•
Pero las elasticidades-precio (propias) de la demanda
son:
(∂x/∂p₁) / (x/p₁) =
-(M/(p₁+p₂)²) / ((M/(p₁+p₂))/p₁ = - p₁/ (p₁+p₂)
(∂y/∂p₂) / (y/p₂) =
-(M/(p₁+p₂)²) / ((M/(p₁+p₂))/p₂ = - p₂/ (p₁+p₂)
Y, similarmente, las elasticidades cruzadas :
•
(∂x/∂p₂) / (x/p₂) = - p₂/ (p₁+p₂)
•
(∂y/∂p₁) / (y/p₁) = - p₁/ (p₁+p₂)
179

180. Comparación de elasticidades-precio de la
demanda
180

181. Comparación de elasticidades-ingreso de la
demanda
181

182. 2. Sin trabajar mucho y utilizando el resultado de las demandas
marshallianas de la función Cobb-Douglas, encuentre las
correspondientes demandas marshallianas en el problema del
consumidor
Maximizar (x-1)2(y-2)3
sujeta a 3x+ 4y =18
¿Por qué este problema involucra “niveles mínimos de subsistencia” ? [Sugerencia: Haga X=x-1, Y=y-2 y escriba el
problema completo en términos de X y Y. Luego utilice las
fórmulas de las demandas para utilidades tipo Cobb-Douglas.]
182

183. 4) a) Definir la noción de curva de Engel y calcular estas
curvas para la función Cobb-Douglas, la función Leontief, y
la función U(x , y) = √x + y.
b) Definir las “trayectorias de expansión del ingreso”.
5) A partir de la trayectoria de expansión del ingreso, dar la
definición de bien de lujo y de bien necesario. También
definir lo que es un bien Giffen.
Solución
La "trayectoria de expansión del ingreso“ puede torcerse más
hacia un bien que hacia otro; es decir, en la medida que aumenta
el ingreso se consume, proporcionalmente, más de un bien
(bien de lujo) que de otro (bien necesario). Recordemos que la
"trayectoria de expansión del ingreso" se calcula tomando
las demandas marshallianas como ecuaciones paramétricas que
dependen del parámetro de ingreso (M).
183

184. Por ejemplo, en la Cobb-Douglas U=x y, la trayectoria está
determinada por los puntos (x,y) tales que x= M/2p1, y =M/2p2.
Y para dibujarla, notemos que esa trayectoria está determinada por la ecuación y= (p1/p2)x.
y
Trayectoria de expansión
del ingreso y= (p1/p2)x
x
184

185. Por su parte, un bien Giffen (Robert Giffen
(1837-1910)) está definido para M fijo, pero
precios variables. Si el precio de un bien baja y la
demanda por ese bien también baja, entonces ese
bien es Giffen. Así, si ∂x/∂p1 > 0 entonces x es
bien Giffen, y si ∂y/∂p2 > 0 entonces y es un bien
Giffen. Por consiguiente, un bien Giffen viola la ley
de la oferta y la demanda. Cabe advertir que los
bienes Giffen no son comunes.
185

186. x es bien Giffen:
p1 disminuye y
x disminuye
•
•
x disminuye
p1 disminuye
186

187. “Como ha señalado Mr. Giffen, un aumento en el
precio del pan genera una pérdida de recursos en
las familias trabajadoras más pobres, y provoca
un aumento en la utilidad marginal del dinero
tales que obligan a dichas familias a recortar su
consumo de carne y alimentos más caros. Siendo
el pan todavía el alimento más barato al cual
pueden acceder, las familias consumirán más del
mismo. ”
Alfred Marshall- Principles of Economics (1895)
187

188. 6. Completar la tabla de abajo:
188

189. Interpretar los coeficientes α y β de la
función de utilidad Cobb-Douglas
U(x , y) = xαyβ
en términos de elasticidades. [Sugerencia:
muestre que α= ∂U/∂x / U/x ].
8) Calcular la elasticidad-precio de la demanda
X=3-2p en diferentes puntos y observar que no
coinciden. Ahora calcular lo mismo con la demanda X=p-α y comprobar que la elasticidad es
siempre la misma (es decir, -α ).
7)
189

190. 8) Definimos las proporciones de la renta gastada por un consumidor, así:
s1= p1x/M
;
s2 = p2 y/M
Calcule estas proporciones para:
a) U(x, y) = xαyβ [Respuesta: s1= α/(α+β), s2= β/(α+β)]
b) U(x, y) = Min {x, y} [Respuesta: s1= p1/(p1+p2), s2=p2/(p1+p2)]
c) U(x, y) = x + y
d) U(x, y) = √x + y
Nota: Note que s1+s 2=1, y observe que para ciertas funciones de utilidad,
estas proporciones son constantes e independientes del mercado. Y, en cambio,
para otras dependen de los precios; es decir, sí dependen del mercado.
190

191. ¿Existirá alguna función de utilidad entre las descritas en a),b),
c) ó d), que permita estudiar cierto hecho empírico que
afirma que a mayor ingreso menor el porcentaje gastado en
alimentos?
Noticia Portafolio del 29 de julio de 2012: Voceros del Grupo
Éxito indican que el gasto mensual de los hogares de clase
media en Colombia se distribuye así: 52% es para
alimentos; 16% para textiles; 25% en durables y 6% en
hogar.
9. Calcular las demandas marshallianas, la utilidad indirecta,
la función de gasto y de las demandas hicksianas de
U( x, y) = (x-1)2(y-3)4 sujeta a p1x + p2y= M. [Sugerencia:
Haga X=x-1, Y=y-3 en la función de utilidad y escriba
la restricción presupuestaria así: p1X + p2Y = M - p1 -3p2.
Haga entonces m=M-p1-3p2 (asuma que esta m es
positiva) , y proceda a resolver el problema típico CobbDouglas que resultó.]
191

192. Solución
X = 2m/6p1 = m/3p1 ,
Y = 4m/6p2 = 2m/3p2
Es decir,
x-1 = m/3p1
;
y-3 = 2m/3p2
y así, utilizando que m=M-p1-3p2, llegamos a que
las demandas marshallianas son:
x* = 1 + (M-p1-3p2)/3p1
y* = 3 + 2(M-p1-3p2 )/3p2
192

193. Ahora calculamos la función de utilidad indirecta
reemplazando las demandas marshallianas en la
función de utilidad, para obtener:
V= (x*-1)2(y*-3)4 = [(M-p1-3p2)/3p1]2 [2(M-p1-3p2)/3p2 ]4
Después obtenemos la función de gasto haciendo, en la
utilidad indirecta, V=U0 y M=e:
U0 = 24(e- p1-3p2)6 /36 (p1)2 (p2)4
Y despejando
e de aquí, llegamos a la función de gasto:
e- p1-3p2 = 2 – 2/3[36 (p1)2 (p2)4 U0] 1/6
= 3 (2 – 2/3)(p1)1/3(p2)2/3(U0)1/6
193

194. o bien, la función de gastos es:
e = 3(2 – 2/3) (p1)1/3(p2)2/3(U0)1/6 + p 1 + 3p2
Y derivando el gasto con respecto a p1 y a p2, obtenemos las dos demandas hicksianas:
h1 = (2 – 2/3) (p1) -2/3 (p2)2/3 (U0)1/6 + 1
h2 = (2 1/3) (p1) 1/3 (p2)-1/3 (U0)1/6 + 3
194

195. 10) Cuál es el signo (positivo o negativo) de la
elasticidad-ingreso de un bien normal? ¿y la
de un bien inferior?
11) Falso o verdadero: “Si una curva de demanda es
elástica en el precio, el gasto en ese bien cae
cuando el precio sube”.
12) Discutir mediante gráficas la noción de concavidad estricta en una y varias variables.
195

196. EJERCICIOS
COMPLEMENTARIOS PARA EL
ESTUDIANTE
1) Un consumidor tiene un presupuesto de $90 para la
compra de dos bienes (x e y). El bien x cuesta $7 por
unidad y el bien y cuesta $3 por unidad. Sin embargo,
el Gobierno ha decidido subsidiar la compra de las dos
primeras unidades del bien.
i) Dibujar la restricción presupuestaria.
ii) Ahora suponga que el consumidor tiene una función de
utilidad U(x , y)=Min{2x, y} y encuentre, gráficamente,
las demandas marshallianas.
iii) Imagine una situación “real” que se adapte a este tipo
de problema (una distinta al de los zapatos derechos e
izquierdos, o al del café con una cucharadita de azúcar).
196

197. 2) Encuentre las demandas marshallianas de un consumidor
que tiene como función de utilidad U(x, y)= 2ln(1+x)
+ 3ln(1+y) bajo la restricción presupuestaria 3x+2y
=70.
3) Encuentre las demandas marshallianas de un consumidor
que tiene como función de utilidad U(x,y)=
(1+x)2(1+y)3 bajo la restricción presupuestaria 3x+2y
=70.
4) Compare las soluciones en 2) y 3). Explique su respuesta.
5) En los ejercicios 2) y 3) anteriores, resuelva el mismo
problema pero con restricción presupuestaria
p1x+p2y=M. Después calcule las funciones de gasto y
las demandas hicksianas.
197

198. Interpretar los exponentes de la función
de utilidad Cobb-Douglas
U(x , y) = x2y3
en términos de elasticidades.
6)
198

199. CLASE MAGISTRAL #4
- EFECTO INGRESO Y EFECTO
SUSTITUCIÓN
- EXCEDENTE DEL CONSUMIDOR
199

200. Ya sabemos que la demanda de un consumidor bajo
competencia perfecta depende de su ingreso (renta)
y de los precios.
Ahora: hemos estudiado una medida de la demanda
ante variaciones porcentuales de la renta o de los
precios: es la noción de elasticidad.
Sin embargo, aún no conectamos, simultáneamente,
ambos efectos, es decir, ¿cuál es la relación de un
cambio de precios con un cambio en la renta? El
efecto renta y el efecto sustitución (Hicks (1939))
son dos medidas de la demanda que nos ayudarán
a responder completamente a esta pregunta.
200

201. (Vector de) Efecto sustitución (sobre la
misma curva de nivel)
M/p₂ •
(Vector de) Efecto ingreso
• A
•
C
M/p₂’ •
Presupuesto original
B•
( Vector de) Efecto precio
•
M/p₁
M’/p₁
201

202. En la gráfica anterior se ilustra el caso en
que, inicialmente, surge un aumento del precio p₂
, dando origen a una disminución en el consumo del
bien y, y a un aumento en el consumo del bien x.
Sin embargo, esto dio origen a un descenso en el
“nivel de vida” (bienestar).
Luego tratamos de compensar este descenso de
bienestar, mediante un aumento en la renta.
Pero, una vez allí, en el nivel de bienestar original, se
hace necesario sustituir cierta cantidad del bien x
por cierta cantidad de y (sin perder el nivel de
bienestar) para regresar al estado de consumo inicial
que se había afectado por el alza inicial en el precio
del bien y. El consumidor sustituye x por y porque
este último aumentó su precio relativo.
202

203. Para medir exactamente el valor de estas variaciones
(vectores), se tiene una colección de ecuaciones
fundamentales en la teoría del consumidor que se llaman
las ecuaciones de Slutsky (del economista ruso
Eugene Slutsky (1880-1948)):
Efecto precio (o total)
∂x/∂p₁
Efecto sustitución
=
∂h₁/∂p₁
Efecto ingreso
+ (-∂x/∂M)x
∂y/∂p₁ = ∂h₂/∂p₁ + (-∂y/∂M)x
∂x/∂p₂ = ∂h₁/∂p₂ + (-∂x/∂M)y
∂y/∂p₂ = ∂h₂/∂p₂ + (-∂y/∂M)y
(1)
(2)
(3)
(4)
En particular, con ellas se pueden obtener las demandas
hicksianas a partir de las demandas marshallianas.
203

204. Ilustración de la ecuación de Slutsky
∂x/∂p₂ = ∂h₁/∂p₂ + (-∂x/∂M)y
(+)
(+)
M/p₂ •
(-)
Efecto sustitución
∂h₁/∂p₂
A(x , y)
•
C
•
Efecto renta
(-∂x/∂M)y
M/p₂’ •
•
B
Efecto precio
∂x/∂p₂
•
M/p₁
M’/p₁

205. Ilustración de otra ecuación de Slutsky:
∂y/∂p₂ = ∂h₂/∂p₂ + (-∂y/∂M)y
(-)
(-)
(-)
M/p₂ •
Efecto sustitución
∂h₂/∂p₂
A(x , y)
•
C
•
Efecto renta
(-∂y/∂M)y
M/p₂’ •
•
B
Efecto precio
∂y/∂p₂
•
M/p₁
M’/p₁
205

206. Un ejercicio sencillo
En el problema
Maximizar
Sujeta a
x2y
3x+2y=45
Y si el precio de x aumenta en un 20%, calcule los efectos precio,
ingreso y sustitución.
Solución
Las demandas marshallianas iniciales de este problema son:
x*= 2(45)/( 3)(3)= 10 ,
y*= (45)/(3)(2)= 7.5
Si aumenta el precio del bien x en 20%, las nuevas demandas
marshallianas son
x**= 2(45)/( 3)(3.6)= 8.33 , y**= (45)/(3)(2)= 7.5
206

207. Para regresar al nivel de utilidad original, recurrimos a
la recta presupuestal 3.6x+2y=50.816 (que es paralela a
la segunda recta presupuestal 3.6x+2y=45). Y las nuevas
demandas serán:
x*** = 2(50.816)/( 3)(3.6) = 9.41
y*** = (50.816)/(3)(2) = 8.47
Chequeemos que, efectivamente, tienen el mismo nivel
de utilidad:
U(x*,y*) = U(10,7.5) = 750
U(x***,y***) = U(9.41,8.47) = 750
207

208. Por lo tanto, el efecto precio (0 total) EP está dado por la diferencia entre las segundas y las primeras demandas marshallianas:
EP = ( 8.33 - 10, 7.5 - 7.5) = (-1.67, 0)
El efecto ingreso (o renta) EI es la diferencia entre las segundas y
las terceras demandas marshallianas:
EI = (8.33 - 9.41, 7.5 - 8.47) = (-1.08, -0.97)
El efecto sustitución ES es la diferencia entre las terceras y las
primeras demandas marshallianas:
ES = (9.41 - 10, 8.47 - 7.5) = (-0.59, 0,97)
Note que:
EP = ES + EI
Pregunta: ¿Cómo calculé el presupuesto M= 50.816 de arriba?
R/ Calculando el gasto e(3.6, 2, 750). Aquí se ve que la función de
gasto es una función de “compensación presupuestal” de los
hogares ante cambios en los precios.
208

209. Efecto ingreso y efecto sustitución en el
ejemplo anterior
Efecto total
(9.41, 8.47)
∙
Demanda inicial
∙
(8.33, 7.5)
∙
(10, 7.5)
Efecto
ingreso
Efecto
sustitución
3x+2y =45
Demanda inicial
3.6x+2y =45
∙
∙ ∙
3.6x+2y = 50.816
209

210. Algunas ecuaciones de Slutsky en nuestras funciones
de utilidad
1. En la función de utilidad de Cobb-Douglas
U(x ,y ) = x y
Comprobaremos una de las cuatro ecuaciones de Slutsky:
∂x/∂p₁ = ∂h₁/∂p₁ + (-∂x/∂M)x
(Efecto precio = Efecto sustitución + Efecto ingreso)
En primer lugar, se tiene que
x = M/2p1 ,
y = M/2p2
210

211. Y, por lo tanto,
∂x/∂p1= -M/2(p1)²
(Efecto precio)
Además, como la función de utilidad indirecta es
V= M²/4p1p2
Entonces la función de gasto (haciendo V=U, M=e)
es
e= 2√U√p1√p2
y como
h1= ∂e/∂p1= (√U√p2) / √p1
211

212. entonces
∂h1/∂p1= - ½ √U√p2 (p1)(-3/2)
Pero como
U = M²/4p1p2
entonces
∂h1/∂p1 = -½ √ U√p2 (p1)(-3/2)=
= (- ½) √(M²/4p1p2) √p2 (p1)(-3/2)
= - M/(4 (p1)2)
(Efecto Sustitución)
212

213. De otro lado,
-(∂x/∂M)x = -(1/2p1)(M/2p1)= -M/(4(p1)2)
(Efecto ingreso)
Por lo tanto,
Efecto precio =
Efecto sustitución + Efecto ingreso
213

214. Efectos ingreso y sustitución en la función
Cobb-Douglas
∂y/∂p₁
=
∂x/∂p₁
=
Efecto precio (o total) =
∂h₂/∂p₁
∂h₁/∂p₁
Efecto sustitución
+
+
+
(-∂y/∂M)x
(-∂x/∂M)x
Efecto ingreso
214

215. 2. En la función de utilidad Leontief
U(x ,y) = Min{x, y}
comprobaremos una de las cuatro ecuaciones de
Slutsky:
∂y/∂p₁ = ∂h₂/∂p₁ + (-∂y/∂M)x
(Efecto precio = Efecto sustitución + Efecto ingreso)
215

216. Pero antes, analicemos gráficamente el problema de dos bienes que no
pueden sustituirse entre sí, y en donde vemos que un aumento en
precio puede compensarse solo con presupuesto:
No existe efecto
sustitución
M/p2•
A=C
•A
M/p2’•
•
B
A partir de la línea
amarilla, este es el
presupuesto después
de un aumento en el
ingreso
Presupuesto inicial
Presupuesto después de un aumento en p₂
en el presupuesto inicial
216

217. Mostraremos entonces que, efectivamente, el
efecto sustitución es nulo en la función de
utilidad Leontief (recuérdese que los bienes
aquí son complementarios).
Partiendo de las demandas marshallianas
x = M/(p₁+p₂) = y
Obtenemos la función de utilidad indirecta
V= min{M/(p₁+p₂), M/(p₁+p₂)}= M/(p₁+p₂)
217

218. Y haciendo allí V=U₀ y M=e, tendremos que
U₀ = e/(p₁+p₂)
O bien,
e= (p₁+p₂) U₀
Y por el Lema de Shephard,
h₂=∂e/∂p₂= U₀
de donde
∂h₂/∂p1=0
(efecto sustitución)
218

219. Por su parte,
∂y/∂p₁ = -M(p₁+p₂)² (efecto precio (o total))
-(∂y/∂M)x = -(1/ (p₁+p₂))(M/(p₁+p₂))= -M(p₁+p₂)²
(efecto ingreso)
Por lo tanto,
Efecto precio =
Efecto sustitución + Efecto ingreso
219

220. Otro ejemplo gráfico: Función de utilidad lineal
U(x , y) = x + y con p2>p1: efecto sustitución nulo
y
A partir de la recta amarilla,
esta es la recta presupuestal
después de un aumento de ingreso
Recta presupuestal original
Recta presupuestal después
de un aumento de p₁
•B
•A
Aumento de p₁ pero todavía con p2 > p1
Efecto ingreso
x
220

221. EXCEDENTE DEL CONSUMIDOR
En palabras simples, el excedente de consumidor
(Dupuit (1844), Marshall (1890)) es una medida
de bienestar que consiste en la diferencia entre
lo que un consumidor está “dispuesto a pagar”
por una mercancía, y lo que realmente paga,
al precio del mercado.
221

222. Ya sabemos que, bajo utilidad marginal decreciente (concavidad estricta de la función de utilidad), un consumidor que solo consume una mercancía, demanda una cantidad x tal que
U’(x) = p
donde p es el precio por unidad de la mercancía
x. Por lo tanto, su demanda marshalliana es:
x= (U´)-1(p)
222

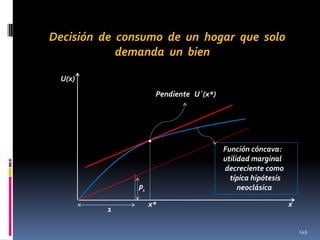
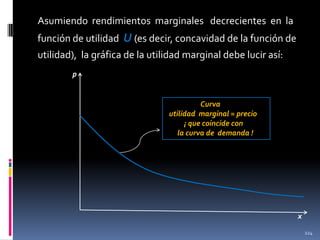
223. Ejemplo
Si U(x)=√x entonces de la ecuación
U’(x)=p
se obtiene que
1/(2√x) = p
(*)
[utilidad marginal = precio]
Y así la demanda marshalliana es:
x= 1/4p²
(**)
¡¡ Las curvas (*) y (**) son las mismas !!
223

224. Asumiendo rendimientos marginales decrecientes en la
función de utilidad U (es decir, concavidad de la función de
utilidad), la gráfica de la utilidad marginal debe lucir así:
p
Curva
utilidad marginal = precio
¡ que coincide con
la curva de demanda !
x
224

225. U´(x)=utilidad
marginal
=p=precio
dispuesto a
pagar por
el consumidor
Excedente del consumidor
Lo que se paga por la compra de x₀ unidades
al precio p₀ de mercado
•
p₀ = precio del
mercado
por unidad
(exógeno al
consumidor)
x₀
x
225

226. Ejemplo simple de excedente del consumidor
p
Excedente del consumidor = $ 4
5
Lo que se paga por la compra de 4 unidades
al precio $3 por unidad = $ 12
precio de mercado
= 3•
Curva de demanda
x = 10 - 2p
4
10
x
226

227. OBSERVACIONES FINALES DE LA
TEORÍA DEL CONSUMO
En primer lugar, analizaremos cómo es que se puede
utilizar todo el sistema del modelo de consumo que
hemos estudiado en clase, para hacer comparaciones
de bienestar de hogares y, por lo tanto, políticas
públicas y sociales centralizadas.
Todo, como es de esperarse, depende de que nuestras
funciones sean implementables econométricamente
basándonos en datos observables.
227

228. 1.
1 Analicemos el siguiente cuadro:
Problema principal del consumidor
Maximizar U(x , y)
sujeta a p1x+p2y=M
Demandas marshallianas
x*(p1,p2,M), y*(p1,p2,M)
Implementables
econométricamente
Roy
Función de utilidad indirecta
V(p1,p2,M)
Implementable
Econométricamente
(si se conoce la
función de utilidad)
228

229. 2. Y ahora analicemos este otro cuadro:
Problema dual del consumidor
Minimizar p1x+p2y (gasto)
sujeta a U(x , y)= U0
Demandas hicksianas
(h1)*(p1,p2,U0),
(h2)*(p1,p2,U0)
Shephard
Función de gasto
e(p1,p2,U0)= p1(h1)* + p2(h2)*
229

230. Ahora: Si la función de utilidad indirecta es
observable (es decir, implementable econométricamente a partir de datos observables
(por ejemplo, encuestas)), podemos, según
hemos hecho en el curso, calcular la función
de gasto y, por lo tanto, esta función también es observable (aunque de manera indirecta).
230

231. Una vez tengamos construida la función de gasto e(p1,p2, U0), se
especifican diversas medidas de bienestar de los hogares. Por
ejemplo, una a la que se recurre es el índice de costo de vida (ICV):
I = [e(p1’,p2’, U0) / e(p1, p2,U0)] x 100
que es el cociente de gastos de los hogares ante un cambio de
precios de mercado de (p1,p2) a (p1’, p2’). Si este índice es
mayor que 100, se requiere de mayor ingreso para mantener el
mismo nivel de vida U0. Pero si es menor que 100, es posible
ahorrar y aún mantener el mismo nivel de vida U0. Es usual recurrir
a e(p1, p2,U0) como el gasto en el año base. Actualmente, en
Colombia, este año base es el 2008.
 -----------------------------------------------------------------------------------(*) El índice de precios al consumidor (IPC) mide la variación de los precios de un mes con respecto a
otro mes de referencia, para un conjunto de bienes y servicios representativos del consumo de
los hogares colombianos. El cálculo del IPC para Colombia lo hace mensualmente el Departamento Administrativo Nacional de Estadística (DANE).
231

232. Ejemplo del cálculo de índice de nivel de vida
Recordemos que si el consumidor tiene una función de
utilidad U(x , y)= x y, entonces la función de gasto es
e = 2(U₀ p₁ p₂)½
Así, si p1 = p2 = 1, y hay un alza de 20% en el precio del
bien 1 (p1=1.2) pero no en el bien 2, entonces el índice
de vida será
I = [2 (U₀ (1.2) (1))½ / 2 (U₀ (1)( 1))½] x 100
= √1.2 x 100 = 109 > 100
Por lo tanto, se requiere de un mayor ingreso para recuperar el nivel de vida anterior (U0). ¿Cuánto es ese ingreso? Esto lo responde el efecto-ingreso a través de la
ecuación de Slutsky.
232

233. Índices de Precios al Consumidor (IPC) en Colombia (2009-2012)
Período base: Diciembre de 2008 (100,00)
Fuente: DANE
233

234. Finalizamos esta introducción a la teoría del consumo mediante
un cuadro conceptual que muestra que, en general (es decir, en
muchas ocasiones, aunque no siempre), podemos deducir cualquiera
de nuestras funciones a partir de una sola de las otras.
Función de
utilidad
Demandas
marshallianas
Si conocemos la
función de utilidad
Utilidad
indirecta
Identidad de Roy
Ecuaciones
de
Slutsky
Mecanismo del ejemplo 7
Magistral 2. No siempre
efectivo
Hacer
V=U0, M=e
Definición de gasto
Demandas
hicksianas
Funciones de gasto
Lema de Shephard
234

235. Tareas para la clase con el profesor asistente
1) Un consumidor tiene la misma función de utilidad
U(x , y) = x + y
pero con restricción presupuestal 2x+3y=18.
Mediante una buena gráfica, responda lo siguiente:
a) ¿Cuáles son las demandas? ¿Qué nivel de utilidad
(bienestar) máxima alcanza?
b) Si el precio del bien x aumenta 25%, ¿cuál será el
ingreso adicional necesario para mantenerse en el
mismo nivel de bienestar anterior? ¿Se requiere de un
efecto sustitución para regresar a las demandas
originales antes del aumento de precio?
c) Las mismas preguntas que en b), pero ahora lo que
sucede es un aumento del 10% en el bien y.
235

236. 2) Comprobar una de las cuatro ecuaciones de Slutsky
cuando el consumidor tiene la función de utilidad
U(x , y) = x½y½
3) Falso o verdadero:
a) En general, el efecto sustitución es negativo o cero.
b) Si un bien es normal, el efecto ingreso “refuerza” el
efecto sustitución.
c) Para que un bien sea Giffen es necesario que sea un
bien inferior. Más aún, el efecto ingreso debe “dominar” al efecto sustitución.
(Sugerencia: Podría requerirse observar la ecuación
de Slutsky).
4) Explicar brevemente la noción de “Preferencias
Reveladas”.
236

237. 5) Mostrar
que una curva de demanda tal como x=M/p
se puede “linealizar” tomando logaritmos a ambos lados
de la ecuación, y escribiéndola de la forma
X= a - b P
para ciertas constantes a y b con b >0. Recurriendo a esto último, “linealizar” las demandas marshallianas de la función
Cobb-Douglas.
6) Convénzase de la siguiente afirmación del profesor titular:
“Ya habíamos discutido que, en general, la ecuación de
equilibrio del consumidor U’(x)=p se tiene para funciones de
utilidad cuasilineales de la forma U(x) + y, en donde nuestra
preocupación se centra en el bien x y el bien y (ye) es “el resto
de las mercancías”; además de que colocamos el precio del bien
y (ye) como numerario.
237

238. Esto implica que cuando calculamos el excedente del
consumidor, éste es una buena medida del bienestar del
consumidor debido a que coincide con la utilidad del mismo.
Además, debemos notar que al construir una curva de
demanda (cantidad x versus precio p) ignoramos el
presupuesto, y esto se debe a que el efecto ingreso para el bien
x, en una función cuasilineal, es nulo. Todo lo anterior se hace
convenientemente, pues el propósito fundamental del curso es
el estudio del equilibrio parcial (oferta = demanda) de un
sólo bien (el bien x), sin explicitar los cambios en el ingreso de
los consumidores (aunque, como veremos, es tenido en cuenta
de una forma distinta).”
238

239. 7) Comentar sobre la existencia de diferentes índices
de precios al consumidor (Laspeyres, Paasche y
Fisher, etc.).
8) Definir Funciones de utilidad homotéticas y probar
que tienen demandas con elasticidad-ingreso igual a
1, lo cual implica que cambios en el ingreso no
afectan la composición del consumo.
9) (*)Definir la noción de elasticidad de susti-
tución, explicar por qué es útil, y estudiar este
concepto en el caso CES, Leontief y CobbDouglas, partiendo de la primera, y llegando a
la segunda y a la tercera como casos límite.
10) (*) Estudiar dos etapas en el consumo (elección
intertemporal). (Sugerencia: Texto Varian intermedio, Cap. 10)).
239

240. 11)
Estudiar la elección del consumidor cuando su presupuesto
incluye renta y un salario:
(El problema de la decisión de oferta de trabajo: el ocio como
un “bien”). Supongamos que un consumidor escoge entre dos
opciones, consumo c (que es un bien) y mano de obra L (que es
un “mal”), y que además tiene un ingreso (renta) m que no
depende de los salarios devengados. Sus gustos por el
consumo y el trabajo están determinados por una función de
utilidad U de la siguiente forma: puesto que la mano de obra es
un “mal”, recurrimos a un “bien” que llamaremos “ocio” y que
podremos describir así: Si Ľ es el número de horas disponibles
en el período de estudio, y l es el número de horas trabajadas
en el mismo período, entonces L= Ľ - l es el número de horas
de ocio que “disfruta” el consumidor; por lo tanto, según lo que
aprendimos en el curso, planteamos el problema de este
consumidor así:
Maximizar U(c , L)
sujeta a pc + wL= wĽ + m
240

241. donde p es un índice de precios al consumidor y w
es el salario por hora. Haga ahora M= wĽ + m , y
estudie las condiciones de equilibrio a la manera
usual enseñada en clase.
Ahora, como un ejemplo, escoja la función de
utilidad Cobb-Douglas
U= c1/2L1/2 y
resuelva, encontrando la oferta laboral l de este
tra-bajador. Decida si, bajo estas hipótesis, un
au-mento en el salario aumenta la demanda por
ocio (pues el aumento en el salario lo hace más
“rico”).
241

242. EJERCICIOS
COMPLEMENTARIOS PARA EL
ESTUDIANTE
1) ¿Por qué dos curvas de nivel de utilidad no
pueden intersectarse?
2) ¿Puede ser que la restricción presupuestaria sea
la misma, incluso en el caso de hogares cuyas
preferencias son diferentes?
3) a) Supongamos que usted desea modelar el
comportamiento de un grupo homogéneo de
consumidores que solo consumen dos bienes complementarios brutos. ¿Cuál función de las
estudiadas en el curso le ayudaría a modelar
mejor la utilidad de este grupo?
b) ¿Y si los bienes fueran sustitutos brutos?
242

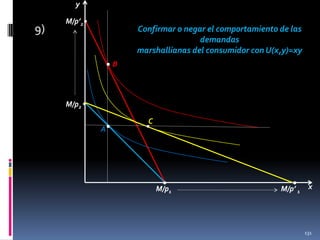
243. 4) [Confirmar o negar los siguientes cálculos]
Encontrar las demandas
marshallianas, la función de utilidad indirecta, la función de gasto y las
demandas hicksianas para la función de utilidad U(x,y) = Min{3x, 2y}
con restricción presupuestaria p1 x+ p2y=M. Ilustre con una gráfica el
problema básico de este consumidor (maximizar la utilidad sujeta a
restricción presupuestaria).
Solución
A partir de 3x=2y se obtiene y= 3x/2. Llevando esto a la restricción
presupuestal obtenemos que p1 x+ p2 (3x/2 )=M. Despejando x, obtenemos que x = 2M/ (2p1+3p2) y, por lo tanto, de y= 3x/2 se obtiene que
y= 3[2M/ (2p1+3p2)]/2 = 3M/(2p1+3p2)
Así llegamos a que las demandas marshallianas son:
x* = 2M/ (2p1+3p2)
;
y* = 3M/(2p1+3p2)
243

244. Ahora calculamos la función de utilidad indirecta reemplazando las
demandas marshallianas en la función de utilidad, para obtener:
V= Min {x*,y*} = Min{3(2M/ (2p1+3p2)), 2(3M/(2p1+3p2))]
= 6M/ (2p1+3p2)
Después obtenemos la función de gasto haciendo, en la utilidad indirecta,
V=U0 y M=e:
U0 = 6e/ (2p1+3p2)
Despejando e de aquí, llegamos a la función de gasto:
e = (1/6)(2p1+3p2) U0
Y derivando el gasto con respecto a p1 y a p2, obtenemos las dos demandas hicksianas:
h1 = (1/3) U0
,
h2 = (1/2) U0
Es decir, los cambios en precios no afectan las demandas , pues los bienes
son complementarios; sólo las afectan los niveles de utilidad Uo.
244

245. 5)
a) Dada su función de utilidad U(x,y)= Min{x, y} + 1, el consumidor
se enfrenta inicialmente a los precios p1=5, p2=2, y tiene una renta de
M=200. Si p1 sube en dos unidades, permaneciendo todo lo demás
constante, ¿cuál es la renta que habría que entregarle en subsidio para
que mantenga intacto su nivel de bienestar? b) Describa las curvas de
Engel de este consumidor. Explique por qué es importante evaluar
estas curvas.
SOLUCIÓN
a) Las demandas marshallianas de esta función de utilidad
Leontief son X=M/(p1+p2) , Y=M/(p1+p2). Y, por lo tanto,
la función de utilidad indirecta es V= M/(p1+p2) + 1.
Haciendo aquí V=Uo y M=e obtenemos la función de
gasto: e = (Uo - 1)(p1+p2) .Y con esto podemos responder
nuestro problema: Puesto que el consumidor se enfrenta
inicialmente a los precios p1=5, p2=2, y tiene una renta de
M=200, entonces
X= 200 /7 = 28,57 ; Y=200 / 7 = 28,57 ; U = 207 / 7 = 29,57
245

246. Después el consumidor se enfrenta a los precios p1=7, p2=2, y
continúa con una renta de M=200. Entonces, X= 200 / 9 =
22,22,
Y= 200 / 9 = 22,22
y U= 209 /9 = 23,22. Recurrimos
ahora a la función de gasto (*) para buscar el ingreso que, a los
nuevos precios, coloque al consumidor en el anterior nivel de
bienestar:
e = (207 /7 - 1)(9) = (200 / 7)(9) = 257, 14
Por lo tanto, se requiere de $57,14 adicionales para regresar al nivel
de bienestar original.
b) Las curvas de Engel de un bien relaciona la variación de la demanda
de ese bien, ante cambios en el presupuesto. Esto, a nivel
agregado, y en principio, permite comparar las demandas entre
distintos “estratos” socioeconómicos. En general, las curvas de
Engel son las mismas demandas marshallianas, cuando los precios
son constantes. En nuestro caso, dada la complementariedad de
los bienes, las curvas de Engel son rectas que pasan por el origen y
tienen pendiente (p1+p2); es decir, las curvas de Engel son:
246
M=(p1+p2)x , M=(p1+p2)y.

247. 6)
Discutir la siguiente nota sobre el mercado del trabajo (muy
importante):
“Conviene no obstante hacer notar que, aunque se pueda asimilar
formalmente a otros bienes, el trabajo tiene la particularidad de ocupar
un sitio importante, y hasta único, en el ingreso de los hogares. En tales
condiciones, toda variación en la tasa de salario provoca un efecto
ingreso no del todo despreciable, que acaba por obstaculizar el efecto
substitución. En esta forma, un incremento salarial incita a disminuir el
tiempo de descanso, ya que éste cuesta más caro, como “tiempo
perdido” por no trabajar, y en consecuencia por la oferta de trabajo, ya
que el consumo se sustituye por descanso. Pero, al mismo
tiempo, como el aumento de salario implica el aumento del poder de
compra, puede ser racional tomar la decisión de consagrar más tiempo
al descanso y trabajar menos; este efecto ingreso actúa en el sentido
opuesto al efecto sustitución, de tal manera que no se puede afirmar a
priori cuál es el efecto de una variación del salario sobre la oferta de
trabajo, incluso si se retienen las hipótesis usuales de la microeconomía. Digamos que los marginalistas ya habían efectuado tal
constatación; por lo demás, admitieron que la curva de la oferta de
trabajo podría ser decreciente, al menos en algunas partes”.
7) Falso o verdader0: “El excedente del consumidor también puede
interpretarse como la cantidad de dinero que sería preciso dar al
consumidor para que renunciara a todo el consumo de un bien”.
247

248. 8) ¿Cuál es la composición actual (año
2012), según el DANE, de la canasta básica
del IPC (Canasta Familiar)?
9) Leer Varian intermedia (capítulos del 2 hasta
el 8).
248

249. Una significativa aplicación: ¿impuesto a las
ventas o impuesto a la renta?
Supongamos que el gobierno desea recaudar una
cierta cantidad colocando un impuesto t a las
ventas (en cierto producto) o su equivalente en
un impuesto a la renta. El problema a decidir
es cuál de los dos tipos de impuesto incide
menos negativamente en el bienestar de los
hogares.
249

250. Para ello, asume que, inicialmente, la restricción presupuestal del
hogar es
p₁ x + p₂ y = M
Por lo tanto, después del impuesto a las ventas para el bien 2, la
restricción presupuestal del hogar es
p₁ x + (p₂+t)y = M
Si (x*,y*) es el nivel de consumo después del impuesto a las ventas,
entonces lo recaudado es t y*. Así, la restricción bajo impuesto a la
renta será
p₁ x + p₂ y = M - t y*
250

251. Con impuesto a la renta (punto C) se
reduce menos el bienestar que con el
impuesto a las ventas (punto B): el efecto
ingreso impacta menos en el bienestar que
el efecto precio (efecto total).
p₁ x + p₂ y =M
M/p₂ •
p₁ x + (p₂ +t) y = M
(con impuesto a las ventas)
A
•
C
M / (p₂+t) •
•
•
B(x*, y*)
•
p₁ x + p₂ y = M - t y*
(con impuesto a la renta)
(M - t y*)/p₁
M/p₁
251

252. NOTA
SI
E L P R O F E S O R A U X I L I A R N O H A LO G R A D O
DESARROLLAR, DENTRO DE LAS SESIONES
DE
S U C L A S E , TO D O S LO S
EJERCICIOS
ASIGNADOS A LA CLASE AUXILIAR, SE LES
E N V I A R Á A S U S C O R R E O S , O S E C O LO CARÁN
EN
LA
F OTO C O P I A D O R A
DE
E D G A R , YA R E S U E LTO S , A Q U E L LO S E J E R C I C I O S Q U E Q U E D E N P E N D I E N T E S . E S TO
N O I N C L U Y E LO S E J E R C I C I O S C O M P L E M E N TA R I O S , Q U E Q U E D A N B A J O L A R E S PONSABILIDAD DE CADA ESTUDIANTE.
252

253. ANUNCIOS
IMPORTANTES
TALLER OFICIAL #1: SE REALIZARÁ EN LAS CLASES DEL 5
y 6 DE SEPTIEMBRE CON SUS CORRESPONDIENTES GRUPOS
Y PROFESORES AUXILIARES. SERÁ TOMADO DE LOS EJERCICIOS COMPLEMENTARIOS (QUE DEJÉ AL FINAL DE CADA
CLASE MAGISTRAL EN LAS DIAPOSITIVAS), Y/O DE EJERCICIOS SIMILARES A LOS ESTUDIADOS EN CLASE (MAGISTRAL O CON LOS PROFESORES AUXILIARES).
PARCIAL #1: SE REALIZARÁ EL MARTES 11 DE SEPTIEMBRE
EN CLASE. INCLUYE LO ESTUDIADO EN LAS PRIMERAS
CUATRO CLASES MAGISTRALES; ES DECIR, LA “TEORÍA DEL
CONSUMO”.
253

254. CLASE MAGISTRAL # 5
PRINCIPIOS
DE LA
TEORÍA DE LA PRODUCCIÓN
Y
MAXIMIZACIÓN DEL BENEFICIO
254

255. Así como la teoría neoclásica del consumidor se basa
en la función de utilidad, también la teoría
neoclásica de la producción se basa en su propia
función: la función de producción.
Una función de producción es una función explícita
que transforma insumos en productos. Es la “caja
negra” de la teoría de la producción, pues resume
de una manera “reduccionista”, todo el proceso
productivo interno de la empresa o firma.
Se sugiere que la aparición de la primera función de
producción en la literatura económica es en Knut
Wicksell (1895).
255

256. En nuestro curso, estudiaremos funciones de producción de solo uno o dos insumos y un producto. La generalización a más de dos insumos es directa e inmediata;
sin embargo, la generalización a varios productos es
mucho más complicada (economías de alcance). Resumiendo, en nuestro curso una función de producción es
una función de la forma
ℝ+
x
o de la forma
ℝ+
f(x)
ℝ²+
ℝ+
( x, y)
f(x , y)
256

257. Allí, x e y nos indican las respectivas cantidades de
esos insumos, y z= f(x , y) es la cantidad producida
con esos insumos. Asumiremos que tanto y= f(x) como
z=f(x , y) son funciones diferenciables, y que, además:
i) En el primer caso,
f’(x) > 0
(producción marginal positiva)
ii) Y en el segundo caso,
∂f/ ∂x > 0
,
∂f/∂y > 0
(producciones marginales positivas)
257

258. Tabla de producción con solo un insumo
Número de horas
trabajadas
5.000
Cantidad de maíz
producido
(en quintales= 46 kg)
95.000
6.000
120.000
7.000
140.000
8.000
155.000
9.000
165.000
10.000
170.000
11.000
171.000
258

259. Gráfica de la función de producción anterior
Miles
de
quintales
171
95
•
5
•
•
•
•
•
11
Miles de
horas trabajadas
259

260. Tabla de producción con dos insumos
f(x , y)= x½ y1/3
Insumo x
Insumo y
Producción
f(x , y) = x½ y1/3
1
1
1
1
2
21/3
2
2
2 1/2 2 1/3
5
3
5 ½ 3 1/3
6
3
7
4
6 ½ 3 1/3
7 ½ 4 1/3
8
5
8½ 5
1/3
260

261. Función de producción con dos insumos
z
z = f(x ,y)
f(x , y)
•
(x , y)
x
261

262. Funciones de producción con dos insumos
y sus curvas de nivel
Un requerimiento esencial en la teoría del
consumidor es que las curvas de nivel tengan la
forma típica ya discutida en el curso (convexas al
origen), y, por lo tanto, el requerimiento general
(excepto en casos muy especiales) sobre las
funciones de utilidad es que sean “cuasicóncavas estrictas”.
262

263. Y aunque las curvas de nivel de las funciones
de producción típicas serán similares a las de
las funciones de utilidad, la justificación para que
ello sea así, es completamente distinta a la que
planteábamos para el caso del consumo (es decir,
que los agentes preferían “combinar” a “especializarse”).
263

264. La razón de esto es, en principio, que
dentro de la epistemología neoclásica de
que tenga que existir un principio optimizador (“principio de mínima acción”), se deciden porque ese principio sea el de la
maximización del beneficio de la empresa
(ingresos por ventas menos costos de
producción), y para que esto sea posible, en
general, se requerirá que las funciones de
producción (con uno y dos insumos) tengan
una característica que estudiaremos más
adelante: rendimientos decrecientes a
escala.
264

265. Es decir, que si duplico los insumos, la producción
aumenta en menos del doble; si triplico los insumos,
la producción aumenta menos del triple; etc.
En particular, se sabe (aunque no lo probaremos aquí) que, en el caso de dos insumos, las
funciones con rendimientos decrecientes a
escala forman curvas de nivel convexas
(estrictas) al origen, similares a las que
conocemos en la teoría del consumidor.
265

266. Función de producción con rendimientos
decrecientes a escala (dos insumos)
z
z = f(x ,y)
f(x , y)
•
y
Curva de isoproducto
(x , y)
x
266

267. Un criterio tecnológico de clasificación de las
funciones de producción: los rendimientos a
escala de una función de producción
1. Rendimientos decrecientes a escala (o
deseconomías de escala)
f(t x, t y) < t f(x , y)
t>1
Ejemplos: Producción
agrícola no tecnificada,
etc.
tf(x*)
y = t f(x)
•
f(tx*)
x*
•
y = f(x)
tx*
Ilustración para una función con un solo insumo
267

268. Es corriente asociar los rendimientos decrecientes
a escala con:
1. Un factor fijo: por ejemplo, la tierra.
2. Ineficiencia tecnológica.
3. Ineficiencia administrativa: dificultades en la organización, coordinación e integración que surgen en la administración de una empresa.
4. Número grande de trabajadores: puede no funcionar tan bien como los pequeños equipos.
268

269. 2. Rendimientos constantes a escala
f( t x, t y ) = t f(x ,y)
t>0
y=t f(x)
t f(x*)= f(tx*) •
•
•
f(tx*)
t f(x*)
x*
y=f(x)
tx*
Ilustración para una función con un solo insumo
269

270. 3. Rendimientos crecientes a escala (o economías
de escala)
f(t x, t y) > t f(x , y)
t>1
Ejemplos: Telecomunicaciones, Internet,
Formación de capital
humano, etc.
y = t f(x)
y=f(x)
•
f(tx*)
tf(x*)
•
x*
tx*
Ilustración para una función con un solo insumo
270

271. Sin embargo, debido a costos fijos (por ejemplo,
arriendos, instalación, etc.) y a otras razones, es
posible que una función de producción luzca así:
f(x)
Etapa con rendimientos
crecientes a escala
•
Etapa con rendimientos
constantes a escala
x
271

272. Ejemplos sencillos
1. f(x)= √x es una función con rendimientos
decrecientes a escala: Si t > 1,
f(t x) = (t x)½ = t½ x½ < t x½= t f(x)
2. f(x)= k x (k es constante) es una función con
rendimientos constantes a escala: Si t > 0,
f(t x) = k(t x) = t(k x) = t f(x)
3. f(x)= x² es una función con rendimientos
crecientes a escala: Si t > 1,
f(t x) = (t x)² = t² x² > tx² =t f(x)
272

273. Un resultado muy útil para saber cuándo una función de producción
de un solo insumo tiene rendimientos decrecientes a escala, es el
siguiente:
“Toda función de producción f(.) cóncava estricta, con
f(0)=0, tiene rendimientos decrecientes a escala”
Con él se puede demostrar que, por ejemplo, las funciones f(x)= xα
para 0<α<1 y f(x) = ln (1+x) tienen rendimientos decrecientes
a escala, pues basta recordar un resultado del cálculo diferencial que
afirma que una función de producción es estrictamente cóncava
si, y sólo si, la segunda derivada es estrictamente negativa.
273

274. 4. f(x , y)= Min{x , y} es una función de producción
con rendimientos constantes a escala, pues si t > 0
entonces
f(t x, t y) = Min{t x , t y} = t Min{x , y}
= t f(x , y)
5. f(x , y) = √x + √y
es una función de producción
con rendimientos decrecientes a escala pues si t >1,
entonces
f(t x, t y) = (t x)½ + (t y)½
f(t)=t1/2
= (t½) (x½) + (t½) ( y½)
= (t½)(x½ + y½)
< t(x½ + y½)
= t f(x , y)
1
f(t)=t
274

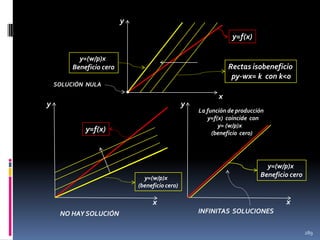
275. 7) Un caso muy importante: la función Cobb-Douglas
f(x , y) = xα yβ.
Aquí,
f(t x, t y) = [t x]α [t y]β
= [tα+β] xα yβ
= [tα+β] f(x , y)
Por lo tanto,
i) Si α+β<1 entonces tα+β < t si t > 1, y así f(x , y)
tiene rendimientos decrecientes a escala.
ii) Si α+β=1 entonces tα+β = t si t > 0, y así f(x , y)
tiene rendimientos constantes a escala.
iii) Si α+β>1 entonces tα+β > t si t > 1, y así f(x , y)
tiene rendimientos crecientes a escala.
275

276. Al igual que en la teoría del consumo, los exponentes α
y β de la función Cobb-Douglas f(x , y)= xαyβ son también elasticidades:
∂f/∂x / (f / x) = α [xα-1y β] / [xα-1 yβ]
= α = elasticidad de la producción con
respecto al insumo x
A esta elasticidad también la llaman la “intensidad”
del insumo x en la producción. Así, si el insumo x
aumenta en 1% entonces la producción aumentará
en α%.
276

277. Similarmente, se muestra (ejercicio) que
β = (∂f/∂y) / (f/y)
= elasticidad de la producción con respecto
al insumo y.
También a esta elasticidad la llaman la “intensidad” del insumo y en la producción. Así, si el
insumo y aumenta en 1%, entonces la producción aumentará en β%.
277

278. Por ejemplo, en el caso de la función de producción
con rendimientos decrecientes a escala Cobb-Douglas
f(L,K)= L½ K ¼ donde
L = horas-hombre
K = unidades de capital (horas de uso de
maquinarias, etc.)
se tiene que esta empresa es más intensiva en mano
de obra (1/2) que en capital (1/4).
278

279. Rendimientos a escala de diversas actividades del sector manufacturero
canadiense 2000-2010 estimadas mediante una función Cobb-Douglas
f(L,K)=LαKβ con L= mano de obra y K = capital.
Mano de obra (α)
Capital (β)
Escala (α+β)
Máquinas de ejercicio
estático
o.64
0.18
0.82
Fábricas de tejido de
punto
0.55
0.36
0.91
Fábricas de zapatos
0.82
0.18
1.00
Fábricas de medias
0.55
0.46
1.01
Fábricas de bloques y
ladrillos
0.93
0.40
1.33
Fábricas de pinturas de
pared
0.71
0.61
1.32
279

280. 8) Otro caso importante: La función CES (Constant
Elasticity of Substitution)
f(x , y)= [x ρ + y ρ] 1/ρ , ρ < 1, ρ ≠0
tiene rendimientos constantes a escala, pues si
t>0, entonces
f(t x, t y) = [(t x) ρ + (t y) ρ)] (1/ ρ)
= [t ρ (xρ + yρ)] (1/ ρ)
= t [xρ + yρ] (1/ρ)
= t f(x , y)
Honrando el nombre de esta función, el parámetro
ρ mide una elasticidad de sustitución que estudiaremos más adelante.
280

281. El problema principal del productor: Maximización del beneficio para funciones de producción
Siguiendo el precepto neoclásico de optimización
de alguna función objetivo sujeta a restricciones,
los productores maximizarán la función beneficio:
∏ = ingresos por ventas
menos
costos de los insumos
Pues, si no maximizan el beneficio, perderán dinero y esto podría llevarlos fuera de la industria.
281

282. Estudiaremos dos casos bajo competencia perfecta:
1) En el caso de una empresa (imaginaria) que
opera con un solo insumo y= f(x), el problema al
que se enfrenta el empresario es:
Maximizar ∏ = p y - w x
sujeta a y = f(x)
donde
p = precio de mercado por unidad del producto
w = costo por unidad del insumo x.
282

283. 2) Y en el caso de una empresa que opera con
dos insumos z= f(x , y), el problema al que se
enfrenta el empresario es:
Maximizar ∏ = p z - w₁ x - w₂ y
sujeta a z = f(x , y)
donde
p = precio de mercado del producto
w₁= costo por unidad del insumo x
w₂= costo por unidad del insumo y
283

284. Profundicemos primero en el primer caso:
Maximizar ∏ = p y - w x
sujeta a y = f(x)
se reduce a
Maximizar p f(x) -w x
Si asumimos que f(x) es cóncava estricta entonces,
derivando e igualando a cero, obtenemos que
p f´(x) – w = 0
o bien,
p f´(x)= w
(ingreso por productividad marginal = costo marginal del
insumo)
o, equivalentemente,
284

285. f´(x*) = w/p
Ecuación de equilibrio del productor
(con sólo un insumo)
que afirma que, para maximizar el beneficio, el productor debe requerir del mercado un nivel de insumos
x* tal que su productividad marginal coincida con el
“costo real” w/p del insumo x.
y
f(x*) = Producción óptima
y=f(x)
•
Rectas isobeneficio
py-wx= k (>0)
y=(w/p)x (beneficio cero)
pues es equivalente a
py-wx=0
x*
x
285

286. Y a partir de la ecuación de equilibrio del productor,
llamaremos en adelante:
x* = demanda de insumo por parte
del productor
f(x*) = oferta de producto al mercado por
parte del productor
∏*=p f(x*) – w x* = beneficio recibido por el
productor
286

287. Y aquí comenzamos a entender que la noción de concavidad
es fundamental al proceso de maximización del beneficio.
Notemos en la gráfica siguiente que si f(x) tiene rendimientos
crecientes a escala, no es posible la maximización del beneficio.
y
y=f(x)
y=(w/p)x
(beneficio cero)
x
287

288. Y también notamos que si la producción tiene
rendimientos constantes a escala, entonces no
existe solución , no se produce absolutamente
nada o, en caso extremo, puede tener múltiples soluciones:
288

289. y
y=f(x)
y=(w/p)x
Beneficio cero
Rectas isobeneficio
py-wx= k con k<0
SOLUCIÓN NULA
•
y
y
y=f(x)
y=(w/p)x
(beneficio cero)
x
La función de producción
y=f(x) coincide con
y= (w/p)x
(beneficio cero)
y=(w/p)x
Beneficio cero
x
x
NO HAY SOLUCIÓN
INFINITAS SOLUCIONES
289

290. Una aplicación “importante”
Si f(L) es una función de producción con rendimientos decrecientes a escala que tiene como único insumo la mano de obra
L, entonces la condición de maximización del beneficio
f´(L*) = w/p
nos asegura que la cantidad óptima de mano de obra a contratar, L*, es tal que su productividad marginal coincida con el
salario real w/p. Es de aquí que parte la teoría neoclásica de
formación de salarios por productividad marginal: esta última te
da, exactamente, cuántas unidades del bien que produces, puede comprar el trabajador con su salario.
290

291. Un ejemplo
Supongamos que nuestra función de producción es de la
forma f(x) = xα para 0<α<1 (recordemos que α, aquí, es
la elasticidad-insumo de la producción). Sus gráficas son
una familia de funciones cóncavas de la forma siguiente:
y=f(x)
y=x
y= x¾
y=x½
y=x¼
y=0
x
291

292. Para maximizar el beneficio de esta empresa
∏ = p xα – w x
hacemos ∂∏/∂x = 0. Es decir,
pαxα-1 – w = 0
o, despejando,
x = (w/pα)1/(α-1)
lo que nos lleva a
x* = (pα/w) (1/ 1- α)
(Demanda por el insumo)
292

293. La oferta de producto al mercado es:
f(x*)= (pα/w) α/ 1- α
Y el beneficio obtenido es:
∏* = p f(x*) - w x* = K p 1/ 1- α w –α/ 1- α
donde
K = (α) α/ 1- α - (α) 1/ 1- α
Y se ve que ambos son directamente proporcionales
al precio de venta del producto, e inversamente
proporcionales al costo por unidad de los insumos.
293

294. Tareas para la clase con el profesor
auxiliar
1. ¿Es un vendedor de dulces a la entrada de la
universidad, un productor de los descritos
por la teoría del curso? Si es así, ¿cuáles son
los insumos? ¿cuáles son los productos?
¿Qué escala podría tener este pequeño
negocio? (Sugerencia: La respuesta es “Sí”)
2. Encontrar la demanda de insumos, la
oferta de producto y el beneficio máximo si la
tecnología es f(x)= ln (1+x), p= $10, w=$2.
3. Definir lo que es una función homogénea de
producción y relacionarlo con los rendimientos a escala.
294

295. 4. Si una función de producción f(K,L) (K=capital,
L=horas-hombre) es homogénea de grado 1
(f(tK,tL)= t f(K,L) para todo t >0), demostrar que
esta función puede ser expresada en términos percápita: F(K,L)= Lf(k,1) donde k=K/L. ¿Por qué es
interesante este resultado?
5. En el ejemplo que aparece en la diapositiva 291, haga
α=1/2 y responda lo siguiente:
a) ¿Qué mide exactamente α ?
b) ¿Cuál es la demanda por el insumo?
c) ¿Cuál es la oferta del producto?
d) ¿Cuál es el beneficio que obtiene la empresa?
e) ¿Podría existir un proceso productivo que opere
con un solo insumo?
295

296. CLASE MAGISTRAL # 6
- MAXIMIZACIÓN DEL
BENEFICIO (CONTINUACIÓN)
- MINIMIZACIÓN DE COSTOS
296

297. Recordemos que la condición para maximizar el beneficio de un
productor con función de producción con un solo insumo, y = f(x),
es
f´(x*) = w/p
que afirma que el productor debe requerir del mercado un nivel
de insumos x* tal que su productividad marginal coincida con
el “costo real” w/p del insumo x.
y
y=f(x)
•
Rectas isobeneficio
y = (w/p)x (beneficio cero)
x*
x
297

298. El problema principal del productor: Maximización
del beneficio para funciones de producción (con dos
insumos)
Vamos a centrarnos ahora en el caso de una empresa
que opera con dos insumos z= f(x , y), y que se
enfrenta a:
Maximizar
sujeta a
∏ = p z - w₁ x - w₂ y
z = f(x , y)
O, lo que es igual, a:
Maximizar
p f(x , y) - w₁ x - w₂ y
298

299. planos de isobeneficio
∏ = p z - w₁ x - w₂ y
= constante
z=f(x , y)
z*=f(x*,y*)
(solución)
z=f(x ,y)
(función de
producción)
•
•
(x*,y*)
x
299

300. plano
tangente
z=f(x , y)
z*=f(x*,y*)
(solución)
z=f(x ,y)
•
(x*,y*)
x
300

301. Para estudiar las características analíticas
de esta solución, derivamos parcialmente
(con respecto a x y con respecto a y) la
función de beneficios
∏ = p f(x , y) - w₁ x - w₂ y
e igualamos a cero, obteniendo que:
p ∂f /∂x = w1 ;
p ∂f /∂y = w2
(Ingreso marginal = costo marginal )
301

302. O bien,
∂f /∂x =w1/p ;
∂f /∂y = w2/p
(productividades marginales
= precios reales de insumos)
Y más allá, dividiendo término a término estas
dos últimas ecuaciones, tendremos que:
302

303. (∂f /∂x) / (∂f /∂y) = w1/w2
Ecuación de equilibrio del productor
(con dos insumos)
Esta ecuación de equilibrio es la condición para que la empresa
maximice el beneficio, y se lee:
“En equilibrio, la tasa marginal de sustitución técnica
((∂f /∂x) / (∂f /∂y) ) es igual a la relación de precios de los
insumos (w1/w2).”
Pero… ¿qué significado tiene aquí la “tasa marginal de sustitución
técnica” ?
303

304. De manera similar a lo hecho para la teoría del
consumidor, si escribimos la curva de nivel de
producción que pasa por el punto de maximización del beneficio (x*,y*) como
f(x , y)= k*
donde k*= f(x*,y*), entonces, derivando implícitamente, se obtiene que
(∂f /∂x) dx + (∂f /∂y) dy = 0
o bien,
(∂f /∂x) / (∂f /∂y) = - dy / dx
304

305. Equilibrio del Productor
y
-∂f/∂x / ∂f/∂y = Pendiente de la
curva de nivel
Curva de nivel de
producción
f(x , y) = f(x*,y*)
recta de costo mínimo
w₁ x - w₂ y = w₁ x* - w₂ y*
≈
1
•
(x*, y*)
Pendiente de la recta = -w1/w2
x
305

306. Y así la tasa marginal de sustitución técnica
mide cuánto del insumo y se requiere para
mantener el mismo nivel de producción, si
reducimos en una unidad el insumo x.
En resumen:
Si el empresario quiere maximizar su beneficio,
entonces debe producir en un nivel tal, que la
tasa marginal de sustitución técnica (dada por
su tecnología), iguale a la relación de precios de
los insumos (dados por el mercado).
306

307. ¡La ecuación de equilibrio del productor es,
entonces, una relación entre un “costo de
oportunidad tecnológico” y un “costo de
oportunidad del mercado”!
Sin embargo, esto solo se da bajo rendimientos decrecientes a escala. Es decir, la maximización del beneficio requiere de rendimientos decrecientes a escala.
307

308. Un ejemplo importante de maximización del
beneficio: la función Cobb-Douglas
El problema es:
Maximizar
sujeta a
∏ = p z - w₁ x - w₂ y
z = xαyβ
Aquí, debemos asumir que α+β <1 para que la
función de producción tenga rendimientos decrecientes
a escala.
Recurriendo directamente a las ecuaciones de equilibrio, tenemos que :
308

309. p ∂f /∂x = w1
, p ∂f /∂y= w2
(1)
Y así,
(∂f/∂x) / (∂f/∂y) = w₁/ w₂
Llegamos, en este caso, a que
pαxα-1 yβ = w₁ ;
pβxα yβ-1 = w2
α xα-1 yβ / β xα yβ-1 = w₁/ w₂
(2)
(1’)
(2’)
De (2’) obtenemos, cancelando términos, que
αy/βx=w1/w2
y así,
y= βw1x/αw2
(3)
309

310. Y colocando esta ecuación (3) en la primera ecuación
de (1’) se llega a que
α xα-1 (βw1x/αw2)β = w₁/p
Y así, después de una confiable manipulación algebraica (confirmarlo por sí mismos), encontramos las demandas por insumos:
x* = p1/(1-α-β) / [(w1/α)(1-β)/ (1-α-β) (w2/β)β / (1-α-β) ]
y* = p1/(1-α-β) / [(w1/α)α / (1-α-β) (w2/β)(1-α)/ (1-α-β) ]
310

311. Además, sabemos que la oferta al mercado es igual a
z*= f(x*,y*)= (x*)α (y*)β. Después de manipulación
algebraica confiable se llega a que la oferta de esta
empresa es:
z*= p(α+β) /(1-α-β) / [(w1/α)α/ (1-α-β) (w2/β)β/ (1-α-β) ]
Y también calculamos el beneficio ∏*= pz* – w1x* - w2y*
que recibe esta empresa si opera a estos niveles:
∏* = pz* -w1x*-w2y*
= (1-α-β) p1/(1-α-β) / [(w1/α)α/ (1-α-β) (w2/β)β/ (1-α-β) ]
311

312. Beneficio nulo bajo rendimientos
constantes a escala
En la clase pasada habíamos mostrado que si la producción tiene
rendimientos constantes a escala, entonces no existe solución,
tiene una solución nula (“no operar”) o, en caso extremo, puede
tener múltiples “soluciones”:
y=f(x)
y=(w/p)x
•
No existe solución
Única solución: No operar
La función de producción y=f(x)
coincide con y= (w/p)x : existen
infinitas soluciones
312

313. En la práctica, es corriente escoger, entre los tres
casos, en el que, en condición extrema e interesante,
existe “maximización” del beneficio; es decir, escogemos x* tal que
f(x*) = (w/p) x*
o, en otra forma,
f(x*)/x* = w/p
(producción media = costo marginal real)
Aunque queda claro que, en tal caso, el beneficio es
nulo pues
∏ =p f(x*)-w x* = 0.
313

314. Lo mismo sucede en funciones de producción
f(x , y) con rendimientos constantes a escala y
con dos insumos: escogemos x*, y* tales que
satisfagan la ecuación
∏ = p f(x*,y*) - w1x* - w2y* = 0
Pero, obviamente, allí no se está llevando a cabo
ningún proceso de maximización de la utilidad,
pues esto es imposible. Sobre esto discutiremos
más adelante un poco más.
314

315. El otro problema del productor: Minimización
de costos
En la teoría de la producción, primero estudiamos
el problema de maximizar su beneficio y hemos
encontrado que la ecuación básica (“tasa marginal de sustitución técnica = relación de costos
de insumos”) se satisface solo cuando la función
de producción tiene rendimientos decrecientes
a escala.
315

316. Por su parte, el otro problema que plantearemos en la producción, es el
de minimización de costos,
Minimizar w1x+w2y
sujeta a f(x , y)= z0
donde z0 >0 fijo, es un nivel de producción dado a priori. Es decir, el
problema del productor es tratar de producir la cantidad z0 al menor
costo posible. Algo que favorece este estudio es que no exige ninguna condición esencial de la función de producción f(x , y) excepto
que sea cuasicóncava. No sobra advertir la similitud de este problema
con el de la construcción de la función de gasto del consumidor: basta con
pensar que el consumidor “produce” utilidad, para que la equivalencia sea exacta.
316

317. Para resolverlo, recurrimos al método de los
multiplicadores de Lagrange:
L = w1x+w2y - λ(f(x , y) – z0)
Y calculamos las correspondientes derivadas:
∂L /∂x=0:
w1 = λ ∂f/∂x
(1)
∂L /∂y=0:
w2
(2)
∂L /∂λ=0:
f(x , y) = z0
= λ ∂f/∂y
(3)
317

318. Dividiendo término a término las ecuaciones (1)
y (2), encontramos, de nuevo, la ecuación de
“tasa marginal de sustitución técnica = cociente
de precios de insumos”:
∂f/∂x / ∂f/∂y = w1/w2
(4)
De manera que las condiciones de equilibrio
para la minimización de costos son la ecuación
(4) anterior y la restricción tecnológica
f(x , y)= z0
(5)
318

319. MINIMIZACIÓN DEL COSTO
y
Curva de nivel f(x , y)= z₀
Curvas de isocosto
y*
•
x*
w₁x + w₂y = w₁x* + w₂y*
x
319

320. Equilibrio del Productor
Dados los costos de los factores
en el mercado, si partimos de A,
podemos disminuir costos, mediante sustitución, hasta alcanzar
el punto de equilibrio E.
y
Curvas de isocosto w₁ x - w₂ y = constante
∙A
Equilibrio del productor
∙B
∙C
∙D
E(x*, y*)
Curva de nivel
de producción
z=f(x,y)
•
Pendiente de la recta = -w1/w2
x
Recordemos que a este tipo de procesos, Marshall (1920) los reunía bajo el rótulo
de “Principio de sustitución”.
320

321. Minimización de costos en la función de
producción Cobb-Douglas
El problema fundamental es
Minimizar w1x + w2y
sujeta a xαyβ= z0
Pero como en la restricción es posible despejar
y= (z0 / xα)1/β , entonces nuestro problema se
reduce a:
321

322. Minimizar w1x + w2(z0 /xα)1/β
Derivando con respecto a x e igualando a cero, llegamos a que
w1 = (α/β) w2(z0)1/β x -(α/β)-1
De donde, despejando x, obtenemos la demanda (condicionada) del insumo 1:
x*= (αw2/βw1)β/α+β (z0)1/α+β
y utilizando la restricción tecnológica
da (condicionada) del insumo 2:
y = (z0 / xα)1/β , conseguimos la
deman-
y* = (βw1/αw2)α/α+β (z0)1/α+β
Observemos que la relación de factores NO es constante: y/x=βw1/αw2.
322

323. Y la función de costo es, entonces,
C(z0) = w1x* + w2y*
= [w1 (αw2/βw1)β/α+β + w2 (βw1/αw2)α /α+β] (z0)1/α+β
Y, por ello, la función de costo de la tecnología Cobb-Douglas se
acostumbra a escribir así:
C(z0)= K (z0)1/α+β
donde
K = [w1 (αw2/βw1)β/α+β + w2 (βw1/αw2)α/α+β]
Y el beneficio (no necesariamente máximo) de producir z0 es:
∏ = p z0 - c(z0) = p z0 - K (z0)1/α+β
323

324. Podemos dibujar las tres formas posibles de
la función de costo de la tecnología CobbDouglas
C(z)= K (z)1/α+β
C(z)
α+β = 1
α+β < 1
C(z)
C(z)
z
Tecnología con
rendimientos
decrecientes a escala
Tecnología con
rendimientos
constantes a escala
z
α+β > 1
Tecnología con
rendimientos
crecientes a escala
z
324

325. Se ve entonces que si la tecnología tiene rendimientos decrecientes a escala, el costo marginal de producir una unidad adicional es más alto que si la
tecnología tiene rendimientos crecientes a escala (es
decir, si es una economía de escala). Así, es más
costoso producir marginalmente en una economía
con rendimientos decrecientes que en una economía de escala.
325

326. Otro ejemplo importante: Minimización de costos en la
función de producción Leontief.
El problema, aquí, es
Minimizar w1 x + w2 y
sujeta a Min {x , y} = z0
Este problema se resuelve de manera semejante al
de la minimización del gasto:
x*= y* = z0
(demandas condicionadas de insumos)
Note que estas demandas no dependen de los precios
de los insumos ni del precio de venta.
326

327. Minimización de costos para la función Leontief
f(x,y)=Min{x,y}
y
w1x+w2y= constante
y=x
Min {x , y} = z0
w1x + w2y= (w1+w2)z0
•
x*=z0, y*= z0
x
Observe que la relación de factores es constante: y/x=1
327

328. Y la función de costos es
C(z0) = w1 x* + w2 y* = (w1 + w2) z0
o bien, de manera general,
C(z) = K z
donde
K = w1 + w2
Así, la función de costos de una tecnología
Leontief es lineal. Por su parte, la función de
beneficios es:
∏ = p z0 - c(z0) = p z0 - K z0 = (p - w1 - w2)z0
328

329. Resumiendo, en general, es posible plantear una
correlación entre las tecnologías y las curvas de
costos:
329

330. Enseguida dibujamos las formas típicas de las
funciones de costo (de largo plazo) (aunque hay
algunas excepciones puntuales), y para ello
nos inspiramos en la conveniente función CobbDouglas:
C(z)= K1 z1/α+β ( Costo total)
C’(z)= K1(1/(α+β) ) z (1- α-β)/ α+β (Costo marginal)
C(z)/z = K1 z (1- α-β)/ α+β (Costo medio)
330

331. Clasificación de las curvas de costo (largo plazo)
Rendimientos decrecientes
a escala
Rendimientos constantes
a escala
Costo total
=C(z)
Costo total
= C(z)
z
Rendimientos crecientes
a escala
Costo total
= C(z)
z
z
Costo
marginal
=C’(z)
Costo
Marginal
= C’(z)
Costo
Marginal
= C’(z)
z
z
z
Costo
medio
= C(z)/z
Costo
medio
=C(z)/z
z
Costo
Medio
= C(z)/z
z
z
331

332. Pero…¿y cómo encontramos la función de oferta? Resulta
que después de resolver el problema de minimización de
costos, debemos pasar por un segundo procedimiento: de
nuevo la maximización del beneficio; es decir, resolver
el problema
Maximizar p z – c(z)
z>0
Derivando con respecto a z, e igualando a cero, se obtiene
otra importante ecuación de equilibrio del productor:
332

333. p = c’(z)
Precio de venta = costo marginal
Esta ecuación de equilibrio del productor nos dice que
el nivel óptimo de producción (es decir, la oferta) z*
debe ser tal que si le agregamos “una unidad adicional”,
La variación del costo de producción coincide con el precio
de venta del mercado.
Sin embargo, para que esta ecuación resuelva el problema
de maximización de esta forma , la función c(z) debe ser
convexa estricta, y, por lo tanto, la función de producción
debe tener rendimientos decrecientes a escala.
333

334. Ejemplo Cobb-Douglas
Consideremos la tecnología f(x , y)= xαyβ con α+β<1.
Entonces su función de costos es c(z)= Kz1/α+β, y la
ecuación de equilibrio es p= c’(z)= (1/α+β) K z(1-α-β)/α+β .
Luego la oferta de este producto al mercado es
z* = [(α+β) p/K](α+β)/(1-α-β)
donde ya sabemos que en la constante K están
implícitos los costos de los insumos. Por lo tanto, el
costo total incurrido por llevar a cabo este nivel z*
de producción es c(z*)= K(z*)1/α+β .
334

335. ¿Y cómo calculamos las demandas de insumos
x* y y*? La respuesta está en el Lema de
Hotelling (Harold Hotelling (1931)):
x*= - ∂∏/∂w1 ;
y* = - ∂∏/∂w2
El cálculo de estas demandas de insumos queda
como ejercicio para la sesión con el profesor
auxiliar.
335

336. Tareas para la clase con el profesor auxiliar
1. En los ejemplos presentados en esta clase magistral,
cambiar letras por números concretos y encontrar las
diferentes variables especificadas.
2. Encontrar el costo mínimo de producir y (ye) unidades
mediante una tecnología con un solo insumo f(x)= x1/2.
Hacer lo mismo para f(x)=x2 y compare las dos
funciones de costo que surgen.
3. Encontrar las demandas condicionadas de insumos
y la función de costo para una empresa que opera con
bienes complementarios de la forma
z = f(x , y) = Min {3x,2y}
¿Es posible asociarle un beneficio máximo a esta
empresa?
336

337. 4. a) Mostrar, fácilmente, que el beneficio de una empresa que
opera bajo y=f(x), es cero cuando produzca a un nivel y*
que satisfaga p=c(y*)/y* (es decir, cuando el costo medio de
producir y* iguale al precio de mercado del producto). Y,
claramente, si el precio es mayor que el costo medio, la empresa
está obteniendo ganancias; pero, por el contrario, si el precio es
menor que el costo medio, estará teniendo pérdidas.
b) Probar que el costo medio es mínimo en el nivel de producción que iguale este costo medio c(y)/y con el costo marginal (∂c/∂y). ¿Es esto generalizable a funciones de producción
con dos insumos?
337

338. 5. Recurriendo a los resultados de esta clase
magistral, comparar las demandas de insumos, la
oferta de producto y el beneficio para la tecnología
z = x1/4 y1/4
mediante los dos métodos:
a) Maximización del beneficio.
b) Minimización de costos y después maximización del
beneficio.
338

339. 6. A partir de la función de gasto de la función de
utilidad Cobb-Douglas, deducir la función de costo
de la función de producción Cobb-Douglas. La idea
central de esta similitud es que el problema de la
minimización del gasto en la teoría del consumidor
es, esencialmente, el mismo de la minimización del
costo de “producir” utilidad.
339

340. 7. Una agencia del gobierno de cierto país, estima
que el número de pasajeros transportados (P) entre
dos ciudades de este mismo país, tiene la forma
P = A xαyβ
donde A, α, β >0 son constantes y, además:
x = número de vuelos nacionales
de aerolíneas de
bajo costo.
y = número de vuelos nacionales de aerolíneas de
precio de regular costo.
340

341. Mediante un ejercicio econométrico la agencia estimó que
A=7, α=0.2389, β=0.5384. Con esta información y con lo
aprendido en el curso, construirle a esta agencia la función de costos del sector, la función de oferta, la función de beneficios y las demandas de vuelos nacionales.
8. Halle la combinación de inputs (insumos o factores) (K, L) que
minimizan el coste de producir 550 unidades de producto, teniendo en cuenta que la función de producción es F(K,L) =
10 K0,6 L0,2 y los precios de los insumos son wK = 20 , wL = 11.
341

342. 9. Definir todas las posibles elasticidades de la curva de oferta de
un productor. Mostrar que la curva de oferta x= Apα (α>0) tiene
elasticidad-precio constante α (aquí, A es una constante mayor que
cero). Dibuje algunas de estas curvas para distintos α’s.
10. Definir la noción de elasticidad de sustitución, explicar por qué
es útil, y estudiar este concepto en el caso CES, Leontief y
Cobb-Douglas, partiendo de la primera, para después llegar a la
segunda y a la tercera como casos límite.
11. Escribir otras ecuaciones tipo Hotelling.
12. Si para la función Cobb-Douglas f(K,L)= KαLβ, aumenta la elasticidad
α, decida si el costo aumenta o disminuye. (Sugerencia: Derive la función de costo con respecto a α, y observe su signo.) ¿Qué significa para el sector productivo, el hecho de que α aumente?
342

343. CLASE MAGISTRAL
# 7
- MINIMIZACIÓN DE COSTOS EN
EL CORTO PLAZO
- NOCIÓN DE EQUILIBRIO PARCIAL
COMPETITIVO
343

344. CURVAS DE COSTO DE CORTO PLAZO
Las curvas de costo se acostumbran a distinguir en
“curvas de corto plazo” y “curvas de largo
plazo” de acuerdo a si incorporan o no los costos
fijos. Se cree que, en el largo plazo (grandes
niveles de producción), las empresas “asimilan”
los costos fijos, y así podrán tomar decisiones
libres sobre la utilización de insumos. Pero
también se distingue entre insumos que, en el
corto plazo, son susceptibles de ser utilizados en
cantidades variables y aquellos que no lo son, como
es el caso de la ampliación de la planta de
producción. De acuerdo con ello, todas las
curvas de costo que hemos estudiado hasta
ahora, son curvas de “largo plazo”.
344

345. Cabe anotar que el hecho de que se haga énfasis en
los factores fijos, es porque la mayoría de
empresas bajo rendimientos decrecientes a
escala incorporan alguno de estos; y ya sabemos que la empresa típica en competencia
perfecta es aquella con rendimientos decrecientes a escala. Por lo tanto, lo usual en equilibrio parcial bajo competencia perfecta, es
estudiar el comportamiento de las empresas en
el corto plazo.
345

346. Clasificación de las curvas de costo (largo plazo)
Rendimientos decrecientes
a escala
Rendimientos constantes
a escala
Costo total
=C(z)
Costo total
= C(z)
z
Rendimientos crecientes
a escala
Costo total
= C(z)
z
z
Costo
marginal
=C’(z)
Costo
Marginal
= C’(z)
Costo
Marginal
= C’(z)
z
z
z
Costo
medio
= C(z)/z
Costo
medio
=C(z)/z
z
Costo
Medio
= C(z)/z
z
z
346

347. Para comenzar el estudio de las curvas de costo de corto
plazo, sea:
CT
=
CT = Costo total de
corto plazo
w1x + w2y
Cv = Costos
variables de
corto plazo
+
w3k
CF = Costos fijos
(o generales)
Es decir,
CT
k = insumos fijos,
= Cv + CF
w3 = “costo por unidad” de
insumos fijos
347

348. Entonces definimos:
i)
ii)
iii)
iv)
v)
Costo total medio de corto plazo
=
Costo variable medio de corto plazo =
Costos fijos medios de corto plazo
=
Costo (total) marginal de corto plazo =
Costo variable marginal de corto plazo
CT / z
Cv / z
CF / z
∂CT / ∂z
= ∂Cv / ∂z
E incluimos también aquí las definiciones con la función
C(w1,w2,z) de largo plazo (es decir, sin costos fijos):
i)
ii)
Costo medio de largo plazo = C / z
Costo marginal de largo plazo = ∂C / ∂z
348

349. Ejemplo: Cómo encontrar las curvas de costo en el
corto plazo.
Consideremos el problema de minimizar el costo de una
función de producción Cobb-Douglas de la forma y = f(x , k) =
=xα k β (para 0<α,β) con un insumo variable (x) y un insumo
fijo (k):
Minimizar
sujeta a
w1x + w2k
xα kβ = y
Problema de minimización de costos
en el corto plazo
Curiosamente, aquí no es necesario llevar a cabo ningún proceso
de optimización, sino que, directamente, se obtiene que:
349

350. x
x = y1/α / kβ/α
0<α<1
α=1
α>1
Demanda de corto plazo
y
C(y)
CT(y) = w1x + w2k
= (w1/kβ/α) y1/α + w2k
Costo total de corto plazo
w 2k •
y
350

351. La curva de costo medio de corto plazo tiene formas muy
particulares:
CT(y)/y = (w1/kβ/α) y(1- α)/α + w2k/y
Costo medio de corto plazo
C(y)/y
α< 1 (rendimientos
decrecientes a escala)
α= 1 (rendimientos
constantes a escala)
α > 1 (rendimientos crecientes a escala)
•
Y*0= (α/1-α)α (w2/w1)α kα+β
y
351

352. La curva de costo marginal de corto plazo:
∂CT / ∂y = [w1/(αkβ/α)] y (1-α)/α
Costo marginal de corto plazo
tiene varias formas diferentes, dependiendo del valor de α:
α<1/2
1>α>1/2
α=1/2
y
α= 1
y
y
α >1
352

353. Resumamos las curvas de costo de corto plazo:
Rendimientos decrecientes
a escala
Rendimientos constantes
a escala
Costo
total
Costo
total
y
Costo
marginal
Costo
total
y
y
Costo
marginal
Costo
marginal
0<α< 1/2
y
y
y
Costo
medio
Costo
medio
Costo
medio
y
Rendimientos crecientes
a escala
y
y
353

354. En este mismo ejemplo Cobb-Douglas, y dado su comportamiento típico, haremos un poco de estática
comparativa:
1) En primer lugar, si en la demanda de corto plazo
x = y1/α / kβ/α
hacemos variar el insumo fijo k, entonces aparecerían
las siguientes figuras:
k crece
x
α <1
α =1
α >1
k
crece
y
y
k
crece
y
354

355. 2) En segundo lugar, si en la curva de costo total de
corto plazo
CT(y) = w1x + w2k
= (w1/kβ/α) y1/α + w2k
hacemos variar el insumo fijo k, entonces aparecerán
las siguientes figuras en colores:
CT(y)
Caso α <1
β=1-α
•
k crece
w2k •
Envolvente:
curva de costo total
de largo plazo
•
Y0
Y1
y
355

356. Notemos que, allí, está una justificación de abrir o
no una “sucursal” de la empresa (entiéndase por
esto “ampliar la capacidad de producción”) .
Supongamos que la empresa está operando sobre la
curva de costo total del extremo izquierdo (roja)
de la figura. La empresa abrirá una “sucursal”
si la demanda del mercado requiere un nivel
de producción más allá del punto (Y0), a partir del
cual trabajaría (totalmente) con la siguiente (a la
derecha) curva de costo total (amarilla).
356

357. Y, si el mercado lo requiere, esto lo hará hasta la cantidad
Y1, momento en el cual construiría una nueva “sucursal”
(es decir, tendría que ampliar la capacidad instalada) y
operaría (totalmente) sobre la curva de costo total
siguiente (verde); etc.
Complementando todo lo anterior, pero ya desde el lado
teórico, notamos que si el cambio en el insumo fijo k es
continuo surge una “envolvente” de puntos que conforman un recta (recta naranja) que pasa por el origen.
¡Esta es la curva de costo total de largo plazo!
357

358. Y esto permite hacer una extrapolación útil a nivel
teórico: Imaginemos un conjunto de empresas
del mismo sector (“sucursales”) , todas idénticas y
con rendimientos decrecientes a escala , dentro de un
mercado competitivo. Entonces ellas podrían verse
como “una sola” empresa del sector que utiliza, en
el largo plazo (pues el factor fijo se ha ido haciendo
variable), la recta envolvente como su curva de
costos.Y así, tendríamos que
cT (y) = (constante) y
De manera que en el largo plazo ¡el sector operaría
con rendimientos constantes a escala!
358

359. En modelos computables, es corriente modelar la industria de
empresas
competitivas
(es decir, que operan como
tomadoras de precios) de un mismo sector, mediante una
función
de producción de largo plazo con rendimientos
constantes a escala, basándose, teóricamente, en resultados
como el que acabamos de presentar. Inclusive, se llega a
afirmar que si el PIB de una economía se estima mediante una
función Cobb-Douglas Y=LαKβ, entonces la diferencia entre α+β y
1, es una medida de qué tan cercana está la economía de una
competitiva. Pero todo esto es muy discutible.
Nota
No sobra decir que, aquí, con este ejemplo que acabamos de
estudiar, hemos dado el primer ejemplo del trascendental
problema en microeconomía del paso de lo individual a lo
agregado. Este es, quizás, el problema central de la microeconomía que pretende buscar respuestas macroeconómicas: se
llama “el problema de la agregación”.
359

360. Note también que esto no asegura que en el corto
plazo la industria también se comporte con
rendimientos constantes a escala. En este caso
es usual asumir que el sector se comporta con
rendimientos decrecientes a escala, de manera
similar a las pequeñas empresas que conforman
esa industria.
360

361. En tercer lugar, si en la curva de costo medio de corto
plazo para β =1- α :
3)
C(y)/y = (w1x + w2k)/y = (w1 (y1/α / k β /α ) + w2k)/y
= (w1/k (1- α)/α) y(1- α)/α + (w2k)/y
variamos el insumo fijo k, entonces aparecerán las siguientes figuras:
C(y)/y
k crece
•
•
•
•
Envolvente: Curva de costo medio de
largo plazo (pues el factor k ha ido
variando).
y*0= (α/1-α)α (w2/w1)α k
y
361

362. Los costos de corto plazo siempre están por encima de los costos de
largo plazo
C(y)/y
Curvas de
costo de corto
plazo
C(y)/y
Y0
Y1
•
•
Y0
Primera
“sucursal”
Envolvente:
Curva de
costo de largo
plazo
y
Y1
Segunda
“sucursal”
Tercera
“sucursal”
362
362

363. La envolvente de puntos mínimos (donde el
costo marginal es igual al coste mínimo) es una
recta constante; es decir,
o bien,
CT(y) / y = constante
CT(y) = (constante) y
De manera que esta constante es la misma de la
envolvente de la función de costo total.
363

364. La curva de costo medio de corto plazo es una
herramienta fundamental de análisis microeconómico de una empresa competitiva (es
decir, con rendimientos decrecientes a escala)
por razones:
1) En
primer lugar, porque, en principio,
es fácilmente calculable por parte del empresario a partir de datos observables.
364

365. 2) Porque el empresario competitivo (es decir, con rendimientos
decrecientes a escala), en el corto plazo, tendrá costo
medio mínimo si produce a un nivel y0 (escala mínima de
eficiencia) que iguale al costo medio con el costo marginal de
corto plazo ( (c(y)/y)’ = (yc´(y) – c(y)) / y2=0 implica yc´(y)=c(y) ):
Curva de costo medio de corto plazo
•
y0
Curva de costo marginal de corto plazo
y
Y si quiere maximizar el beneficio, debe producir en un nivel tal
que el precio de mercado iguale al costo marginal de esa producción.
365

366. 3) Porque si el costo medio mínimo es menor que
el precio de mercado del producto, el empresario
sabrá que percibe ganancias. Y, en caso contrario,
estará incurriendo en pérdidas.
Curva de costo medio de corto plazo
p = precio de mercado
Curva de costo marginal de corto plazo
•
Beneficio
Costo medio
en y0 ( = c(y0)/y0)
•
Beneficio = py - c(y) = y0 (p - c(y0)/y0)
y0
= producción óptima
y
366

367. 4) Y esto da pie a entender, recurriendo a la curva de costo
medio, cuándo una empresa puede entrar o no al mercado:
entra si el precio de mercado es mayor que el costo medio
mínimo:
Esta empresa no
entrará en el mercado
Precio de mercado p0
Esta empresa sí entrará
en el mercado
y
367

368. Repasemos las curvas de costo de corto plazo:
Rendimientos decrecientes
a escala
Rendimientos constantes
a escala
Costo
total
Costo
total
y
Costo
marginal
Costo
total
y
y
Costo
marginal
Costo
marginal
y
y
y
Costo
medio
Costo
medio
Costo
medio
y
Rendimientos crecientes
a escala
y
y
368

369. Clasificación de las curvas de costo (largo plazo)
Rendimientos decrecientes
a escala
Rendimientos constantes
a escala
Costo
Total
Costo
Total
y
Costo
Marginal
Costo
Total
y
Costo
Marginal
Costo
Marginal
Costo
Medio
y
y
y
y
Costo
Medio
Rendimientos crecientes
a escala
Costo
Medio
y
y
369

370. Maximización del beneficio en el corto
plazo
-Se recurre al beneficio con los costos de corto plazo
incorporados.
-Aunque se maximice el beneficio en el largo plazo
con beneficios positivos, en el corto plazo podría
suceder que se maximice el beneficio pero éstos
sean negativos (por ejemplo, si los costos fijos son
muy altos), y así, en ausencia de otros incentivos,
será mejor no operar. ¡Y todo esto aún con
rendimientos decrecientes a escala!
-También las curvas de oferta pueden diferir en el
corto y en el largo plazo.
370

371. LA
NOCIÓN DE EQUILIBRIO
PARCIAL COMPETITIVO
Hasta ahora hemos asumido que los precios de
las mercancías están formados, “de alguna
forma”, por el mercado. En esta sección
explicaremos cómo es que la teoría
neoclásica afirma que se lleva a cabo este
proceso de formación de precios para mercados aislados de una economía competitiva.
371

372. En primer lugar, definimos la demanda agregada
por un bien homogéneo como la sumatoria de las
demandas de los n hogares (Xi (p), i=1,2,…,n) por
ese mismo bien:
X(p) = ∑i=1,…,n Xi (p)
En segundo lugar, y de manera similar, definimos
la oferta agregada de un bien como la sumatoria
de las ofertas de las m empresas (Yj (p), j=1,2,…,m)
que producen ese mismo bien:
Y(p) = ∑j=1,…,m Yj (p)
372

373. La teoría del equilibrio parcial bajo competencia
perfecta (Marshall (1890) “Principles of Economics”)
aísla el mercado de ese bien del resto de la
economía, y asume que el precio p del bien se
determina únicamente, mediante la fórmula de
equilibrio del mercado de él:
X(p) = Y(p)
Oferta = Demanda
Dicho sea de paso, la teoría del equilibrio general
(Walras (1874)) se encarga de estudiar la formación
de precios a través de la interconexión de los
mercados; es decir, sin aislarlos.
373

374. No sobra advertir que la demanda y la oferta agregada de un bien privado se calculan horizontalmente.
Por ejemplo, en el caso de la demanda:
p
p
y1
Demanda agente 1
p
y2
Demanda agente 2
•
y1+y2
Demanda agregada
374

375. Y también es pertinente aclarar aquí que la
demanda y la oferta individual es “infinitesimal” comparada con la demanda agregada. Es por ello que, en lugar de una
sumatoria, la demanda y la oferta agregadas
deberían ser expresadas como integrales de las
demandas y de las ofertas individuales, respectivamente.
375

376. Demanda (u oferta) individual en competencia perfecta
Demanda
(u oferta)
agente i
Agentes económicos
El área debajo de la curva es la demanda (u oferta) agregada. Note que
el aporte de la demanda del agente i (línea roja) a la demanda agregada
(área total) es nula.
376

377. Ejemplo sencillo de formación
de precio de equilibrio
Supongamos que, en cierta economía, la curva
agregada de demanda de cierto bien (X) se estima
que es
X = 90 – P
Y que la curva agregada de oferta del mismo bien se
estima regida por la ecuación
X = P/2
377

378. Entonces el precio de equilibrio del bien X, se determina
igualando la oferta y la demanda agregadas : 90 –P = P/2.
Y así, el precio de mercado, el mismo que los agentes
individuales toman como dado, es P*= 60 y, por lo tanto,
la cantidad de equilibrio en el mercado es X*= 30.
P
X = P/2
90
precio de mercado
60
•
30
A este esquema,
Marshall (1890) lo
llamaba
“la tijera”
X = 90 - P
90
X
Cantidad de equilibrio del
bien X, en el mercado
378

379. Cabe anotar que, en competencia perfecta, el
precio es una “señal limpia” del comportamiento del
mercado de ese bien. Así, un productor que quiera
colocar un pequeño negocio de ese producto, sabe
que, a ese precio, seguro , lo podrá vender (recuerde
que su oferta individual es infinitesimal comparada
con la oferta agregada y, por ello, no afectará el
precio de mercado). En la vida real, sin embargo, las
“fallas” del mercado, no permiten que esa venta sea
tan segura.
379

380. Otro ejemplo sencillo de formación
de precio de equilibrio
Para conectar con el trabajo que hemos hecho hasta ahora,
supongamos que un “hogar representativo” de la economía
(es decir, es el único agente de la economía y sus gustos
“representan” los de todos los demás) tiene una función de
utilidad
U(x) = x1/2
(1)
Entonces su demanda está dada por la ecuación de maximización de la utilidad U´(x) = p, donde p es el precio de
mercado. O, lo que es lo mismo,
1/(2√x) = p
(2)
O bien,
x= 1/4p2
(*)
380

381. Por su parte, el “productor representativo” produce x
mediante la función de producción (de corto plazo)
x = AL½
(3)
donde L= horas-hombre y A>0 es constante. Aquí, la
ecuación que nos da la oferta es a través de la maximización del beneficio
∏= p (AL½ ) - w L:
L = (Ap/2w)2
(4)
Y, reemplazando (4) en (3), obtenemos la ecuación de oferta de x:
x =A2(p/2w)
(**)
381

382. Igualando las ecuaciones (*) y (**) de demanda y oferta
de mercado obtenemos 1/4p2 =A2(p/2w). Lo que nos lleva
a que el precio del mercado es
p* = (w/2A2)1/3
Esto, inmediatamente, nos lleva a una pregunta: ¿Cómo se determina w? Y la respuesta es que habrá que
estudiar el mercado laboral correspondiente para determinarlo, también, mediante igualación de oferta y demanda. Solo que, a su vez, este mercado puede depender de
otros precios, y así sucesivamente. Es esto lo que obliga a
pensar en el equilibrio general, y a encontrar limitantes en
la noción de equilibrio parcial.
382

383. “Malas” Noticias: Discontinuidad de la oferta
en el corto plazo
p
Oferta de corto plazo
Aquí asumimos que la “empresa representativa”
no ha empezado a operar y, por lo tanto, no
incurre en costos fijos cuando decide no operar.
Costo medio de corto plazo
•
Y0
Curva de costo marginal de corto plazo
y
py -c(y) ≥ 0 si y sólo si p ≥ c(y)/y
383

384. Problema: ¡¡En el corto plazo podría no haber
equilibrio!!
p
Oferta de corto plazo
Demanda de corto plazo
•
y
384

385. Un problema más: Si las curvas de indiferencia
no son convexas, la curva de demanda puede
ser discontinua y el equilibrio parcial podría no
existir.
y
p1
Oferta
∙
∙
Demanda
∙
∙
∙
∙
∙
x
∙
x
385

386. Otra “inconsistencia” de la economía neoclásica del equilibrio
parcial
Inclusive, si aceptamos la “visión” presentada antes, de que, en el
largo plazo, una industria de empresas competitivas
(rendimientos decrecientes a escala) idénticas puede asimilarse
a una sola empresa con rendimientos constantes a escala,
entonces se acostumbra a afirmar que el beneficio
∏=py–Ky
se maximiza cuando p=K (beneficio cero), y, por lo tanto, la idea
inicial de la tijera marshalliana, pierde sentido porque la oferta
queda indeterminada, y la demanda es innecesaria para
determinar un precio de equilibrio parcial que ya está definido:
p*=K: solo se requiere la demanda para encontrar la cantidad de
equilibrio pues la “oferta” es infinitamente elástica.
386

387. Equilibrio cuando la industria presenta rendimientos constantes a
escala
Esta no es una curva de oferta típica:
es una curva de ingreso marginal; aún
así , es corriente asumirla como la “curva
de oferta” de la industria competitiva con
entrada libre de empresas.
p=K
•
387

388. Estabilidad del equilibrio competitivo:
formación dinámica de los precio
(Modelo de la telaraña (Kaldor (1934) y otros))
p
p
•
Precios a la baja
Precios al alza
Exceso de oferta
Equilibrio
asintóticamente
estable
Exceso de demanda
y0
p
y
•
Equilibrio
estable
y0
•
y
Equilibrio
inestable
y0
y
388

389. Kaldor (1934) probó que el caso de estabilidad
asintótica ocurre cuando la curva de demanda
es más elástica que la curva de oferta en el
punto de equilibrio. Y el caso de inestabilidad
ocurre cuando la curva de oferta es más elástica
que la curva de demanda, en el punto de
equilibrio.
389

390. Tareas para la clase con el profesor
asistente
De los siguientes ejercicios, hacer: 1, 2, 3, 5,
8, 9 y 12. Los ejercicios restantes quedan
a cargo de cada estudiante para realizarlos con los monitores o consultar las
respectivas soluciones en el dossier de
respuestas dejado en la fotocopiadora.
390

391. 1. Definir la noción de excedente del productor de forma similar a como
hicimos en la clase magistral con el excedente del consumidor.
Mostrar su equivalencia con la “renta económica”.
2.
a)
Si en cierto análisis aparecen las curvas de costo como en
las gráficas de abajo, ¿qué tipo de rendimientos a escala
tiene la tecnología y qué plazo (corto o largo) se estaría
estudiando?
Costo marginal
Costo medio
b)
Costo marginal
Costo medio
c)
Costo total
Costo medio
3.
¿Cuál es la demanda agregada de dos consumidores que demandan
así: p1= 3-2y, p2=7-5y ? Dibuje las tres demandas.
391

392. 4. Dados los resultados de esta clase magistral,
encuentre para qué
nivel de producción(en el corto plazo) son iguales el costo medio y el costo
marginal bajo rendimientos decrecientes a escala. En cada uno de los tres
casos, ¿este nivel corresponde al de mínimo costo medio? ¿Será posible
que el costo marginal y el costo medio se encuentren el punto de mínimo
costo medio bajo rendimientos crecientes o constantes a escala, en el
corto plazo? ¿Y en el largo plazo?
5. Un
fabricante puede producir tufinas a un costo de US$ 40 cada
una. Se estima que si las tufinas se venden a X pesos cada una, los
consumidores comprarán 120 – X de estas al mes. Exprese el
beneficio mensual del fabricante como una función del precio.
¿Cuál es el precio óptimo?
392

393. 6. Suponga que una empresa tiene la posibilidad de elegir entre
dos métodos de producción: uno tiene un costo fijo de $50,000 y
un costo marginal de $2,000; el otro tiene un costo fijo de
$120,000 y un costo marginal de $1,000. Trace las curvas de costo
total y medio, correspondientes a los dos métodos. ¿En qué niveles de
producción utilizará la empresa la tecnología de costo fijo bajo?
¿En cuál utilizará la de costo fijo elevado?
7. (Un ejercicio de recapitulación)
Asuma como cierta la siguiente tabla simplificada de cierta empresa
que produce vestidos de novia regida por una función de producción
Y=f(L,K) donde los costos por unidad de L= horas-hombre y K= unidades
de capital (léase, máquinas, etc.) son wL = 1 y wK =7.
393

394. 394

395. a) De acuerdo con los datos, dibuje la función de
producción (con factor fijo) Y versus L. ¿Qué clase de
rendimientos a escala presenta esta empresa?
Explique.
b) De acuerdo a los datos, dibuje las funciones de costo
total, costo marginal y costo medio, a corto plazo.
c) Explique la forma de la función de costo total; en
especial, el significado económico de su convexidad o
concavidad.
d) ¿Qué significado económico tiene la forma de la
función de costo medio? ¿Tiene forma de U?
e) Identifique el costo medio mínimo. ¿Por qué es igual al
costo marginal? Explique.
f) ¿Para qué precio de venta del producto, la empresa
estaría maximizando el beneficio al nivel de insumos
L=15, K=4?
395

396. g) Si el precio de mercado es p=5.55, ¿qué cantidades (mínima
y máxima) aproximadas de mano de obra permitirán a la
empresa obtener beneficios positivos? ¿Y beneficios máximos?
Explique.
h) Si el precio de mercado es p=5.29, si además nuestra
firma representara a la industria en el mercado, y si
estuviese maximizando el beneficio, ¿a cuánto (aproximadamente) debería ascender la demanda de vestidos
para que el mercado estuviese en equilibrio?
i) Si nuestra empresa representara a la industria en el
mercado, ¿cuál es el precio de entrada a la industria?
396

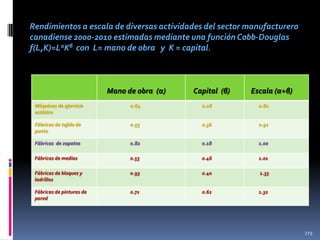
397. 8. a)Si una empresa tiene dos plantas con funciones de
costo C1(y1)= 3(y1)2 y C2(y2)= 2(y2)2 ¿cuál es la función de
costo de la empresa?
[Sugerencia: Primero minimice
el costo total sujeto a y1 + y2= Y.]
b) El mismo problema anterior pero ahora con funciones de
costo C1(y1)= 3(y1)1/2 y C2(y2)= 2(y2)1/2 . [Sugerencia: La
diferencia está en si las empresas tienen costos marginales
crecientes (rendimientos decrecientes a escala) o costos
marginales decrecientes (economías de escala).]
9. En el ejemplo de minimización de costos en el corto
plazo discutida en la clase magistral, muestre que la
función de beneficios (en el corto plazo) es
∏ = p y - [(w1/k(1-α)/α) y1/α + w2k]
397

398. y que la condición de maximización del beneficio es
p = (w1/αk(1-α)/α) y(1- α)/α
Y que, por lo tanto, la función de oferta (corto plazo) es
y = (αα/1-αk/w1α/1-α) pα/1-α
Dibuje las curvas de oferta de corto plazo para α=1/2, α=3/4
y α=1/3.
398

399. 10. Considere la función de producción
f(x , y)= x1/4y3/4
a) Calcule la función de oferta de largo plazo.
b) Calcule la función de oferta de corto plazo haciendo y=k (haga α=1/4 y utilice lo realizado en la clase
magistral).
Dibuje ambas funciones en un gráfico “producción
(eje x) versus precio (eje y)”. ¿Cuál de las dos tiene
mayor elasticidad-precio? Explique la razón de su
respuesta.
399

400. 11. Si la tecnología de una empresa viene
representada por la función
de producción F(L,K) = (K1/2 + L1/2)2, obtenga las demandas condicionadas de factores y la función de costes a largo plazo.
12.Suponga que
la función de producción agregada para la economía
en su conjunto se ha estimado como f(L,K)=L0.75K0.25, donde L= horas
–hombre y K = unidades de capital. Si los mercados fueran perfectamente competitivos, entonces los trabajadores recibirían un 75%
del PIB (producto interno bruto) como ingreso.
[Sugerencia: Aplique la ecuación de Euler que afirma que si f(L,K) es
una función de producción con rendimientos constantes a escala, entonces
f(L,K)= L ∂f(L,K)/∂L + K ∂f(L,K)/∂K .]
400

401. Solución. Puesto que
∂f/∂L = w/p ,
∂f/∂K=r/p
la ecuación de Euler se transforma en
w L + r K = p f(L,K)
(*)
De otro lado, como
(∂f/∂L)(f/L) = 0.75
(elasticidad-trabajo de la producción)
Entonces
(w/p)/(f/L) = 0.75
(**)
y así, wL = o.75pf(L,K).
Comparando (*) y (**) se obtiene el resultado para la mano de obra (L).
Para el capital (K) el procedimiento es similar.
Argumentos como estos se utilizan para el estudio de qué tan apartada
está una economía de la competencia perfecta.
401

402. 13. Un bien tiene las siguientes funciones de oferta y de
demanda:
Qd = 600 -10P ;
Qs = -100 + 10P
a) Encuentre el precio y la cantidad de equilibrio.
b) ¿Cuál es la elasticidad-precio de la oferta y la demanda
en el punto de equilibrio?
14. Dadas las siguientes funciones de oferta y de
demanda:
Qd = 800 -5Pd +5Y -10Py
; Y= 100, Py= 35
Qs = -650 +15Ps +5K +2L
; K= 50, L= 100
donde, Y= ingreso, Py= precio de otro bien, K= capital,
L= empleo:
a) Encuentre el precio y la cantidad de equilibrio.
402

403. b) ¿Cuál es la elasticidad-precio de la oferta y la
demanda en el punto de equilibrio?
c) ¿Cuál es la elasticidad-ingreso de la demanda, allí?
d) El ingreso Y: ¿es sustituto o complementario?
e) ¿Qué sucede con el equilibrio si el ingreso
aumenta en 20%? Efectúe el cálculo y realice un
análisis gráfico.
f) ¿Qué sucede con el equilibrio si el empleo se reduce
en 30%?
15. Análisis de estabilidad del equilibrio competitivo
en el caso de demanda y oferta lineales.
16. Mostrar que, en el corto plazo, una empresa con
rendimientos decrecientes a escala puede tener
pérdidas si los costos fijos son muy altos.
403

404. 17. Discuta la siguiente afirmación: “Partiendo de la oferta, Marshall
definió cuatro períodos puramente artificiales. El período de mercado,
un período de muy corto plazo en el que la oferta es fija, sólo la
demanda influye en la determinación del precio. El período de corto
plazo, en el que la producción puede aumentar porque aumentan los
factores de producción variables de la empresa pero permanece uno
constante (el tamaño de la planta), lo que implica que la tecnología
no varía y que la empresa opera a rendimientos decrecientes y costes
crecientes; estos costes se pueden dividir en costes variables y costes
fijos a corto plazo, costes que determinan simultáneamente con la
demanda, el precio de los bienes. El período de largo plazo en el que la
producción puede aumentar porque aumentan todos los factores y,
por tanto, todos los costes pueden volverse variables de manera que
la curva de oferta a largo plazo puede adoptar la forma de los costes
crecientes, constantes o decrecientes (en el caso de que opere con
costes constantes, los precios de equilibrio a largo plazo sólo estarán
determinados por la oferta). Y el período secular, o de muy largo
plazo, en el que la tecnología y la población varían. Por regla general,
dice Marshall, cuanto más largo sea el período considerado
(excluyendo el período secular) mayor influencia tiene el coste de
producción sobre el valor; al contrario, cuanto más corto sea el
período considerado mayor será la influencia de la demanda.”
404

405. 18. Discutir el equilibrio parcial de bienes intermedios (no sólo
de bienes finales). Por ejemplo, camiones doble-troque,
etc.
19. Si la función de costo de corto plazo es
C(q)= 125 + 2q + q2
determinar el costo fijo, el costo variable, el costo promedio,
el costo fijo promedio y el costo variable promedio.
20. Si una empresa tiene rendimientos decrecientes a escala y
se divide en dos empresas similares, ¿cómo se comportan
los beneficios? Establezca las hipótesis necesarias.
21. Muestre que si la curva de demanda agregada de una
economía es X= a- bP y la oferta agregada es
X= c + dP, donde a, b, c, d son constantes positivas, el
equilibrio parcial del bien X es:
X =(ad+cb)/(b+d)
;
P = (a-c)/(d+b)
405

406. 22. Una función que no tiene un tipo de
rendimientos específico (creciente, constante
o decreciente) es f(x, y)= √x + y . Calcule
su función de costos de largo plazo y
compruebe que no se ajusta a ninguno de
los tres tipos presentados en la tabla de
costos. ¿Será lo mismo en el corto plazo?
Para verlo, asuma que y=k y calcule la
función de costos. Luego asuma x = k > 0 y
haga lo mismo.
406

407. 23. Estudie condiciones sobre la elasticidad de la
oferta y la demanda para que el equilibrio
parcial sea asintóticamente estable. ¿Está esto
relacionado con la sustituibilidad del bien por
“otros bienes”? Explique.
24. Estudiar una función de producción para la
industria del teatro en Colombia. (Cuadernos de
Economía, 2012)
25. En la diapositiva 366, calcular el beneficio de la
industria en términos del salario pagado a sus
trabajadores y que es determinado por el mercado (no por la industria).
407

408. 26. (Teoría cuantitativa del dinero) Discutir sobre la ecuación
cuantitativa del dinero M = kPY (M=masa monetaria nominal
media en circulación (puesta a disposición de la economía por
las autoridades monetarias); P= nivel general de precios; Y=
producción de la economía; k=constante que es la
periodicidad con la que se efectúan l0s pagos de salarios, que
es casi inalterable en el corto plazo) como una ecuación de
equilibrio parcial (igualdad entre oferta y demanda de
dinero). Así, los desequilibrios entre la oferta y demanda de
dinero serían causas de las alteraciones en el nivel general de
precios (P). En numerosas ocasiones, esto es todo lo que se
afirma sobre el papel del dinero en el modelo neoclásico de
equilibrio parcial que estamos estudiando en este curso: el
Banco Central imprimirá dinero de manera proporcional al
valor de la producción de la economía (PIB), para que las
transacciones puedan llevarse a cabo con moneda legal
respaldada por la autoridad monetaria.
408

409. 27. Ilustrar lo siguiente con buenas gráficas:
a. Un aumento de la oferta de un producto
(desplazamiento hacia la derecha de la curva de
oferta) origina un decremento del precio de
equilibrio y un incremento de las cantidades de
equilibrio intercambiadas .
b. Un descenso de la oferta de un producto
(desplazamiento hacia la izquierda de la curva de
oferta) origina un incremento del precio de
equilibrio y un decremento en las cantidades de
equilibrio intercambiadas .
28. Ejercicios CLM.
409

410. CLASE MAGISTRAL #8
- EQUILIBRIO COMPETITIVO CENTRALIZADO Y ÓPTIMOS DE PARETO
-INTRODUCCIÓN A LA TEORÍA DE
FALLAS DE MERCADO
410

411. ¿Por qué es importante encontrar el
equilibrio parcial competitivo de largo
plazo?
Porque es eficiente y, más específicamente, porque es “eficiente en
el sentido de Pareto” ( Vilfredo Pareto (1848-1923)). Veamos.
411

412. Es corriente en la teoría del equilibrio parcial centralizado, construir
una función de bienestar social (o “función de excedente social”
o “surplus social”) del “agente representativo” en el mercado del bien x,
así:
B(x) = U(x) – C(x)
Satisfacción de consumir
x unidades del bien
Costo de producir
x unidades del bien
Pero lo importante aquí es darnos cuenta de cuándo se maximiza esta función
de bienestar, y para ello derivamos e igualamos a cero esta función cóncava
estricta (*) para obtener que:
---------------------------------------------------------------------------------------------------------(*) Aquí, asumimos que las empresas operan con rendimientos decrecientes a escala, que son las empresas
típicas que pueden habitar en competencia perfecta. También asumimos que la función de utilidad tiene
marginalidad estrictamente decreciente.
412

413. U’(x) = C’(x)
Condición de optimalidad social
Pero esta condición de máximo bienestar social se satisface si
recordamos las dos condiciones de optimalidad de los agentes
representativos:
U’(x)= p*
C’(x)= p*
Consumidor
representativo
Productor
representativo
donde p* es el precio de mercado del bien x (que se obtiene
igualando la oferta y la demanda por el bien x). De manera que,
si ambos agentes optimizan, el bienestar social se maximiza. A
esta situación se le llama “óptimo social” en el mercado del bien
x.
413

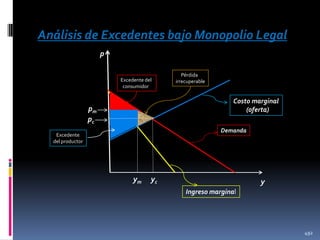
414. Y ahora entenderemos por qué se le conoce
también como un óptimo de Pareto: Podemos
escribir el “excedente social” B(x)= U(x) – C(x),
así:
gasto
ingreso
B(x) = [U(x) – p*x] + [p*x – C(x)]
Excedente del
consumidor
Excedente del
productor
414

415. ¿Y por qué U(x) - p*x es el excedente del consumidor?
Para ello requeriremos de una pizca de matemáticas por
fuera del curso (la integral). Advirtiendo que sólo ocurrirá
aquí, notemos que:
U(x) – p*x = ∫0x (U’(x) – p*)dx
que es el área entre U´(x) y p*, que coincide con el
concepto de excedente del consumidor estudiado en la
clase magistral #4. Aquí asumimos que U(0)=0.
Similarmente para el excedente del productor, p*x – C(x)
con (C(0)=0):
p*x – C(x) = ∫0x (p* – C’(x))dx
415

416. Para entender todo el problema, solo basta
caer en la cuenta de que:
U´(x) = p
Ecuación general de demanda
C´(x) = p
Ecuación general de oferta
y ya la siguiente gráfica aclarará todo:
416

417. Distribución del excedente social
p
C´(x) = p
Excedente del
consumidor
p* = precio de mercado
•
Excedente del
productor
U’(x)=p
x
417

418. De manera que no es posible distribuir de una
manera diferente el excedente social sin que uno
de los dos agentes tome del otro pero llevando
a éste a la ineficiencia.
La distribución realizada por excedentes de esta
manera se llamará un óptimo de Pareto (social). Es
decir, en una distribución del excedente social
que sea óptimo de Pareto (o Pareto-óptima)
ninguno de los dos agentes podrá tomar surplus
del otro sin ocasionarle una pérdida de eficiencia.
418

419. Ejemplo Sencillo
p
$90
p*= $60
$450=
Excedente
del
consumidor
p= 2x
Excedente
del
productor
= $900
p= 90- x
x*=30
90
x
419

420. Frontera Pareto, Frontera de Posibilidades de
Producción y Equilibrio Parcial Centralizado
Es posible extender la noción de óptimo de Pareto a
cualquier número de agentes económicos: una
distribución de riqueza es óptima de Pareto si ninguno puede mejorar su bienestar (medida con la
función de utilidad) redistribuyendo la riqueza, sin
que alguien reduzca su bienestar.
420

421. Por ejemplo, en el caso de dos consumidores,
U1(x) y U2(y), el problema se puede plantear
en dos partes que deben resolverse simultáneamente. Así, (x, y) es un óptimo de Pareto si es
solución a:
Consumidor 1: Maximizar U1(x)
sujeta a U2(y)=Ū2, Ū2 es fijo
x + y = Z, Z fijo
Consumidor 2: Maximizar U2(y)
sujeta a U1(x)=Ū1, Ū1 es fijo
x + y = Z, Y fijo
421

422. Es claro que estos problemas, así planteados,
no requieren de los multiplicadores de Lagrange,
solo de simple sustituciones. Veamos un ejemplo:
Maximizar U1(x) = xα
sujeta a U2(y) = yβ = Ū2
x+y=Z
0< α,β <1
De donde se obtiene, inmediatamente, que
(U1)1/α + (U2)1/β = Z
(*)
que es la frontera Pareto, pues el otro problema
planteado, arroja exactamente la misma ecuación
(*).
422

423. Conjunto y Frontera Pareto
U2
Distribución imposible
para la economía
A•
B •
C •
Distribución posible
y eficiente Pareto
de la economía
Distribución posible
pero ineficiente de
la economía
U1
423

424. En el caso de dos sectores productivos, x=f1(L1)
y y =f2(L2), (con L= mano de obra, y f1, f2, cóncavas
estrictas), el problema también se puede plantear
en dos partes que deben resolverse simultáneamente. Así, (x, y) es un óptimo si es solución a:
Productor 1:
Productor 2:
Maximizar f1(L1)
sujeta a f2(L2)=F2,
L1 + L2 = L,
Maximizar f2(L2)
sujeta a f1(L1)=F1,
L1 + L2 = L,
F2 fijo
L fijo
F1 fijo
L fijo
424

425. Veamos un ejemplo: Para 0< α,β <1,
Maximizar x = (L1 )α
sujeta a y = (L2 )β = F2 (fijo)
L1 + L2 = L
De donde se obtiene, inmediatamente, que
(x)1/α + (y)1/β = L
(*)
que es la Frontera de Posibilidades de Producción
(FPP) (o “Función de Transformación”).
425

426. Conjunto y Frontera de posibilidades de
producción de la economía
y
Producción imposible
para la economía
•
•
Producción posible
pero ineficiente de
la economía
Producción posible
y eficiente
de la economía
•
x
426

427. La FPP es uno de los más sencillos instrumentos de
análisis económico, por cuanto ilustra ideas básicas
de la teoría económica tales como:
i) Eficiencia / Ineficiencia
ii) Pleno empleo de los recursos productivos
iii) Disyuntivas
iv) Costo de oportunidad
v) Crecimiento económico / Retroceso económico
Como todo modelo, se basa en una serie de supuestos:
i) Economía produce dos bienes
ii) Nivel de recursos productivos dado
iii) Nivel tecnológico dado.
427

428. Equilibrio Parcial Centralizado : Frontera
Pareto versus Frontera de Posibilidades de
Producción
y
Frontera de
posibilidades
de producción
Equilibrio parcial
para los bienes x e y
•
Frontera
Pareto
x
428

429. Equilibrio Parcial: Problema de la asignación
eficiente (centralizada) en un mercado competitivo
Isocuantas de utilidad
Maximizar U(x, y)
sujeta a F(x, y)= 0
Vector de precios
de equilibrio
y
Equilibrio parcial
para los bienes x e y
Condición de equilibrio
•
∂U/∂x / ∂U/∂y = ∂F/∂x / ∂F/∂y ( = p1 / p2 )
x
Tasa marginal de sustitución =Tasa marginal
de sustitución técnica
Frontera de posibilidades de
producción
429

430. EXPLICACIÓN:
Maximizar
sujeta a
U(x, y)
F(x, y)= o
Escribimos el lagrangiano
L = U(x, y) + λ F(x, y)
Y derivamos con respecto a
x, y, λ:
∂L /∂x = ∂U/∂x + λ ∂F/∂x = 0
∂L /∂y = ∂U/∂y + λ ∂F/∂y = 0
∂L /∂λ = F(x, y) = 0
Lo que nos lleva a la ecuación de equilibrio centralizado:
(∂U/∂x)/ (∂U/∂y) = (∂F/∂x)/ (∂F/∂y)
430

431. Ejemplo sencillo
Supongamos que la frontera de posibilidades de producción está
dada por
F(x , y) = 3x1/2 + 2y1/2 -1 = 0
donde x= alimentos y y=vivienda. Y supongamos que la economía
tiene una función de bienestar dada por
U(x , y)= x2y
Entonces la asignación óptima la obtenemos igualando la tasa
marginal de sustitución a la tasa marginal de sustitución técnica:
∂U/∂x / ∂U/∂y = ∂F/∂x / ∂F/∂y ( = p1 / p2 )
431

432. Y así obtenemos:
2xy / x2 = 3x-1/2 / 2y-1/2
de donde y= (9/16)x. Y que llevado a la ecuación tecnológica F(x, y) = 3x1/2 + 2y1/2 -1 =0 arroja que:
x* = 4/81
;
y* = 1/36
Por lo que la relación de precios es:
p1/p2 = 2y*/x* = 2(1/36) / (4/81) = 9/8
Así, el precio de mercado del bien x es mayor que el del
bien y.
432

433. Algunas Funciones de Bienestar Social
i) Asignación mediante mercado competitivo.
ii) Función bienestarista: U=λ1U1 + λ2U2
iii) Función rawlsiana: U=Min{λ1U1, λ2U2}
U2
U=Min {λ1U1, λ2U2}
U=λ1U1 + λ2U2
∙
∙
U1
433

434. Justicia versus Eficiencia
El mercado competitivo (ideal, inexistente en la
realidad) es eficiente (en el sentido de Pareto) pero
no incorpora ninguna noción de justicia, excepto, tal
vez una, que es moral: En competencia perfecta
todos los agentes son iguales ante el mercado y
nadie puede sacar ventaja de otro. Hay desigualdad
de posiciones (nacemos en distintas posiciones
socioeconómicas) pero hay igualdad de condiciones
(ante el mercado), decía Walras.
434

435. Competencia Perfecta versus
Libre Mercado
La competencia perfecta no incorpora las categorías de “libre mercado”. La noción de libre
mercado es mucho más general y difusa que la
noción científica de “competencia perfecta”.
435

436. Competencia Perfecta y Capitalismo
Aunque la competencia perfecta incorpora agentes
individuales, propiedad privada y mecanismo de
precios para asignación de recursos, el modelo de
competencia perfecta no es un modelo a escala de
una economía capitalista: en principio, el modelo
de competencia perfecta sólo es un modelo centralizado con “subastador”, que más se parece al
“socialismo de mercado” de Oscar Lange.
436

437. FALLAS DE MERCADO
Algunos casos importantes que rompen con la
condición de competencia perfecta y que conducen, en general, a sub-optimalidad son:
1. Monopolio y Monopsonio
Competencia
2. Oligopolio y Oligopsonio
imperfecta
3. Competencia monopolística
4. Bienes públicos
5. Información asimétrica
6. Impuestos y subsidios del gobierno
7. Etc.
437

438. Competencia según el número de empresas
en el mercado de una mercancía
1 empresa
2 empresas
“Pocas” empresas
(de 3 a 6 aprox.)
“Muchas” empresas
“Infinitas” empresas
•
•
•
•
•
Monopolio
Duopolio
Oligopolio
Competencia
monopolística
Competencia
perfecta
COMPETENCIA IMPERFECTA
438

439. Algunas de las seis fallas de mercado explícitas que
acabamos de mencionar serán estudiadas en
este curso (obviamente, existen “fallas” que no
consideraremos aquí), aunque cada una con
diferente intensidad y profundidad: al fin y al
cabo este es un curso de introducción a la
microeconomía.
Vale la pena resaltar que un alto número de las más
comunes fallas de mercado, están en el sector
productivo de la economía: es más fácil pensar en
consumidores competitivos que en firmas competitivas.
439

440. Por ahora, miremos un ejemplo sencillo de la
ineficiencia que puede causar un impuesto a la luz
de los excedentes del consumidor y del productor.
Imaginemos que, inicialmente, una empresa que
produce tufis mediante la curva de oferta p=2x,
y que además la demanda del mercado por tufis
está compuesta por x=90-p. Luego, el gobierno
decide cargar un impuesto de $20 por unidad.
Veamos los cambios en la situación de equilibrio,
y la aparición de una pérdida de bienestar social (pérdida irrecuperable de eficiencia) conocida
en la literatura como deadweight loss.
440

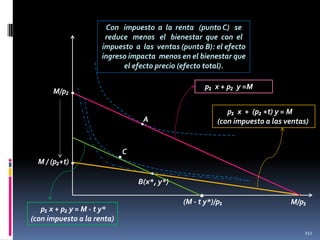
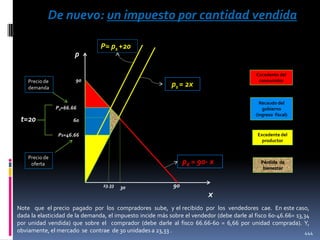
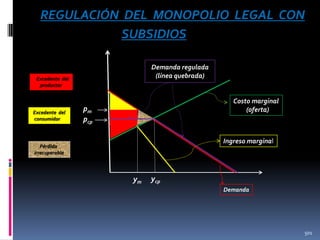
441. p = 2x +20
p
Precio final al
comprador
después del impuesto
Impuesto
20
90
Excedente del
consumidor
p= 2x
Recaudo del
gobierno
(ingreso fiscal)
66.66
60
46.66
Excedente del
productor
Precio de venta
antes de aplicar
el impuesto
al consumidor
p = 90- x
23.33
30
Pérdida
irrecuperable
de eficiencia
90
x
Nota. Recordar que el excedente del productor es igual al ingreso menos los costos variables (Excedente
= ∫[p-C’(y)] dy = py – Cv(y)= py- [C(y) – CF] = beneficio + CF) o, lo que es lo mismo, al beneficio más
los costos fijos . Así, en el largo plazo, el excedente del productor coincide con los beneficios del productor.
441

442. Tipos básicos de impuestos y subsidios
Cuando se impone un impuesto o un subsidio, aparecen
dos precios en el sistema:
i) El precio de demanda (pd), que es el precio pagado
por los compradores del bien.
ii) Y el precio de oferta (ps), que es el precio recibido
por los vendedores.
Existen varios tipos de impuestos y subsidios:
a) Impuesto a la cantidad: pd = ps + t ; ps = pd + t
b) Impuesto al valor:
pd = (1+τ)ps ; pd = (1+τ)ps
c) Subsidio a la cantidad: pd = ps – s ; ps = pd – s
d) Subsidio al valor:
pd = (1-s)ps ; ps = (1-s)pd
442

443. Y las correspondientes condiciones de equilibrio de
mercado son:
i) Impuesto a la cantidad:
D(pd)= S(ps)
pd = ps + t
ii) Impuesto al valor:
D(pd)=S(ps)
pd = (1+τ)ps
etc.
443

444. De nuevo: un impuesto por cantidad vendida
p
Precio de
demanda
P= ps +20
90
Excedente del
consumidor
ps = 2x
Recaudo del
gobierno
(ingreso fiscal)
Pd=66.66
t=20
60
Excedente del
productor
Ps=46.66
Precio de
oferta
pd = 90- x
23.33
30
Pérdida de
bienestar
90
x
Note que el precio pagado por los compradores sube, y el recibido por los vendedores cae. En este caso,
dada la elasticidad de la demanda, el impuesto incide más sobre el vendedor (debe darle al fisco 60-46.66= 13,34
por unidad vendida) que sobre el comprador (debe darle al fisco 66.66-60 = 6,66 por unidad comprada). Y,
obviamente, el mercado se contrae de 30 unidades a 23,33 .
444

445. Pero merece notarse también que si el impuesto
continúa subiendo, el recaudo (ingreso fiscal) cae
debido a que los impuestos altos reducen el tamaño
del mercado. Este es el origen de la curva de
Laffer.
Recaudo
fiscal
Precio
Curva de Laffer
Cantidad
Impuesto
445

446. Incidencia de un impuesto por cantidad
vendida y elasticidad de la demanda
Cuando el la demanda es inelástica (por ejemplo, bienes de primera necesidad sin sustitutos)
es el consumidor ( )quien
paga la mayor parte del
impuesto.
Cuando el la demanda es elástica
(bienes con sustitutos perfectos) es
el productor ( ) quien paga la
mayor parte del impuesto.
446

447. Precios máximos y precios mínimos
1. Precio mínimo: Precio por encima del precio de
equilibrio. Un caso típico es en el mercado
laboral: surge cuando el salario de equilibrio es
inferior al salario de sobrevivencia, justificando así la
existencia del salario mínimo. Sin embargo, ese
objetivo puede generar un exceso de oferta laboral,
es decir, desempleo o informalidad.
2. Precio máximo (o tope): Precio por debajo del precio
de equilibrio. Busca generar un exceso de demanda
que “jalone” el mercado. Un caso típico es el de
precios máximos de arrendamiento.
Qué tan grandes son estos excesos de oferta o de
demanda, dependerá de las elasticidades de estas
curvas.
447

448. Ilustración de precio mínimo: El Problema del
Salario Mínimo
Salario
Demanda de trabajo
por parte de las
empresas
Oferta de trabajo
por parte de los
trabajadores
Salario mínimo
Salario de equilibrio
Mano de obra
Exceso de oferta = desempleo
448

449. Bienestar en el Problema del Salario Mínimo
Salario
Demanda de trabajo por parte de
las empresas
Disminución de
excedente para
las empresas
Oferta de trabajo por parte de
los trabajadores
Salario mínimo
Salario de equilibrio
Aumento de
excedentes para
los trabajadores
Mano de obra
Exceso de oferta = desempleo
449

450. Ilustración de Precio Máximo: El Problema del
Precio de la VIS (Vivienda de Interés Social)
Precio de
vivienda VIS
Demanda de vivienda VIS
Oferta de vivienda VIS
Precio de equilibrio
Precio máximo:
135 SML
Número de viviendas VIS
Exceso de demanda
de viviendas
450

451. El Problema del Precio de la VIS
(Vivienda de Interés Social)
Precio de
vivienda VIS
Excedente del comprador de vivienda
Aumento de
excedente para
los compradores
de VIS
Disminución de
excedente para
el productor
precio máximo
135 SML
Número de viviendas VIS
Excedente del
productor de vivienda VIS
Exceso de demanda
de viviendas
451

452. “Malas” noticias
La noción de excedente del consumidor y del
productor son un buen ejercicio pero sólo para
estudiantes principiantes, pues, en general, es
apenas una medida aproximada (aunque, en
algunos casos, razonable) del bienestar social.
Otras alternativas de medida del bienestar son la
“variación compensada” y la “variación equivalente”, pero ellas están por fuera del alcance
de este curso.
452

453. Tareas para la clase con el profesor
asistente
De los siguientes ejercicios, hacer: 2, 3, 6, 22, 23
y 28. Los ejercicios restantes quedan a
cargo de cada estudiante para realizarlos
con los los monitores También, por
supuesto, el profesor titular y los profesores
auxiliares estamos en disposición de aclarar
las dudas que surjan al realizar estos
ejercicios.
453

454. Tareas para desarrollar con el
profesor auxiliar
1. a) En un mercado competitivo de la papa se establece
el precio de
equilibrio del kilo. Si diez usuales compradores de papa, dejan de
hacerlo, ¿cambiará la curva de demanda? Explique.
b) (Falso o verdader0) Si hay un aumento en la demanda (oferta)
de un mercado competitivo, es porque fue causado por muchos
compradores (vendedores).
c) ¿Podría ser el mercado de obras de arte, un mercado
competitivo? ¿Y el mercado de apartamentos de una zona de la
ciudad? Explique.
d) ¿Podrá darse una figura de oferta-demanda a la manera usual, si
el mercado no es competitivo? ¿O esto es exclusivo de los
mercados competitivos?
e) ¿Se investigarían nuevos fármacos o se produciría nuevo software bajo
competencia perfecta?
f) ¿Nos gustan a los consumidores los bienes homogéneos?
G) ¿En el circuito económico, a dónde van los beneficios obtenidos
por las empresas en el modelo de competencia perfecta?
454

455. 2.
Frente a un equilibrio inicial dado por las curvas
Qd = 200 – 2p y Qs = 60 + 5p, se aplica un impuesto al
consumidor de $5 por unidad vendida. Calcular el
precio y la cantidad de equilibrio previos a la aplicación del impuesto, y graficar la situación inicial en
este mercado. Plantear las nuevas ecuaciones de oferta
y demanda, una vez aplicado el impuesto. Calcular
el nuevo precio y cantidad de equilibrio en el mercado;
aclare cuánto recibirá por unidad el pro-ductor; y
cuánto pagará el consumidor. Calcule la inci-dencia
del impuesto sobre el consumidor y sobre el
productor. Muestre gráficamente y calcule cuál será la
recaudación del gobierno por la aplicación del impuesto.
455

456. 3. Dadas las siguientes funciones de oferta y de demanda:
Qd = 700-5P+5M -10Py
Qs = -550 +15P+5K + 2L
M=110, Py= 30
K=45, L= 120
donde M = ingreso, py= precio de otro bien, K= capital, L=empleo.
a) Encuentre el precio y la cantidad de equilibrio.
b) ¿Cuál es la elasticidad-precio de la oferta y la demanda en
el punto de equilibrio?
c) ¿Cuál es la elasticidad-ingreso de la demanda?
d) El bien “Y”: ¿es un sustituto o complementario?
e) ¿Qué sucede con el equilibrio si el ingreso aumenta en 10%?
Efectúe el cálculo y realice un análisis gráfico.
f) ¿Qué sucede con el equilibrio si el empleo se reduce en 40%?
456

457. 4. Una empresa produce bajo Y=M¼N¼ con precio
inicial p0y utilizando insumos M y N , y con precios
iniciales W0M y W0N , respectivamente. El precio de M
aumentó en un 18% , y el Gobierno quiere evitar que
por esta razón disminuya la cantidad producida de Y.
Por ello, decide dar un subsidio a la firma de z% sobre
el precio inicial de Y , es decir, p1Y = (1 + z%) p0Y. ¿Cuál
debe ser z para que la producción Y no cambie?
5. Considere el caso de una empresa con una tecnología
dada por f(T,L)= T√L donde T , L son el tamaño de la
planta (medido en metros cuadrados) y el número de
trabajadores, respectivamente. El metro cuadrado de
planta cuesta wT y a cada trabajador se le paga wL
por día.
457

458. I) En a), b), c) y d) enseguida, asuma que el
tamaño de la planta no es posible cambiarlo en
el corto plazo; más aún, considérelo fijo en un
nivel de T0. Entonces:
a) ¿Cuántos trabajadores se deben contratar para
producir Q unidades del bien?
b) Muestre que la función de costos de corto
plazo es
C = wLQ2/(T0 )2 + wTT0
c)Dibuje las funciones de costo medio y marginal.
En particular, establezca si son crecientes o
decrecientes, y si una es superior a la otra.
458

459. d) Explique cuánto querría vender el dueño de esta
empresa si pudiese vender la cantidad que quisiera al
precio p , y su motivación fuese únicamente lucrar.
----------------II) Ahora asuma que el tamaño de la planta es variable.
Si el precio p es tal que, en la situación anterior, la
empresa obtiene ganancias, ¿querría el dueño
aumentar el tamaño de la planta?
a) ¿Qué rendimientos tiene esta tecnología?
b) Dibuje las funciones de costo total (de largo plazo),
costo medio y costo marginal.
459

460. c) Explique cuánto querría vender el dueño de esta empresa
si pudiese vender la cantidad que quisiera al precio p , y
su motivación fuese únicamente lucrar.
6. Calcule el nivel de producción óptima que maximice el
beneficio de la empresa con función de costos de corto
plazo c(y)= y2 + (1/y) si el precio de venta es p=2. Haga lo
mismo con la función de costos de largo plazo c(y)= y3/2.
7. Resolver el mismo problema de la diapositiva 419, pero
con un impuesto de $30 al consumidor.
8. Discutir la siguiente afirmación: “Algunos economistas
argumentan que los impuestos al trabajo generan grandes
distorsiones y creen que la oferta de trabajo es muy elástica.
Así, el origen de la curva de Laffer se refiere a la propuesta
de Reagan y Laffer de que una reducción de impuestos
induciría a la gente al trabajo y, en consecuencia, habría
potencial para incrementar los ingresos fiscales”.
460

461. 9. Construir la frontera Pareto si U1(x)=3x1/2 , U2(y)= 2ln y
, x + y =X , donde X es la cantidad fija del bien.
10. Construir la frontera de posibilidades de
producción (FPP) si f1(L1) = (L1)1/4, f2(L2)= (L2)1/2,
L1 +L2= L , donde L es la cantidad (fija) de mano de
obra disponible en la economía.
11. Utilizando la tijera marshalliana oferta-demanda,
decida si es cierta la afirmación de cierto político que
asegura que “un cambio tecnológico reduce el precio
de mercado del producto”.
461

462. 12. Confirmar o negar el ejercicio de la columna derecha.
Impuesto a la cantidad
Subsidio a la cantidad
Impuesto
al comprador
Subsidio
al comprador
p = ps + t
pd
ps
A
B
D
pd
Impuesto al valor
p = (1+τ)ps
ps
C
•
• G
E F •
p = ps - s
H
(Ejercicio)
EC = Excedente del consumidor = A + B + D + E + F
EP = Excedente del productor = B + C+ D + H
Impuesto
al comprador
ps
S= Subsidio = B + C + D + E + F + G
Excedente total = EC+EP –S= A+ B + D + H - G
pd
Pérdida irrecuperable = G
462

463. 13. Con impuesto a las ventas sobre el
comprador, llevar a cabo el mismo ejercicio
que se hizo en la presente clase magistral con
impuesto a la cantidad, incluyendo incidencia,
recaudos y pérdida irrecuperable.
14. La función de transformación (FPP) de una
economía que solo produce los bienes X e Y
con mano de obra mediante X= (L2 )1/4 , Y =
(L1)1/3 donde L1 + L2 = 200 , es X4 + Y3 = 200
Además, si la función de bienestar social es U(X,Y) = Min{X,Y}
(“beneficiar a
quienes tengan menos”) entonces el óptimo
social es X = 3.53 (aprox.)= Y.
463

464. y
x 4 +y 3 = 200
y=x
5.85
U=Min {x,y}
3.53
∙
3.53
3.76
x
Gráfica para el problema 14
464

465. 15. Probar que al resolver el problema:
“Maximizar U(x , y) sujeta a F(x, y) = constante”
se obtiene que:
“Tasa marginal de sustitución = Tasa marginal de
sustitución técnica”
Graficar el problema recurriendo a la frontera de
posibilidades de producción.
16. Encontrar las asignaciones eficientes centralizadas y los precios que permitirían esta asignación de manera descentralizada, si la economía está
regida por
F(x , y) = x1/4 + 5y1/4 ,
U(x , y) = xy3
465

466. 17. ¿Qué sucedería con los precios si en el ejemplo
anterior tuviéramos U(x , y)=Min{x , y}? ¿Son
únicos?
18. Definir y explicar la curva de Lorenz y el coeficiente de Gini como herramientas para medir
la desigualdad en la distribución del ingreso.
466

467. Chile
EE UU
Portugal
Reino Unido
Italia
Canadá
Australia
Japón
España
Corea
Alemania
Holanda
Francia
Suiza
Suecia
Finlandia
Bélgica
Noruega
Dinamarca
COEFICIENTE DE GINI (0=IGUALDAD;
1=DESIGUALDAD)
0.6
0.5
0.4
0.3
0.2
0.1
0
467

468. 19. Evaluar la siguiente afirmación:
“La opinión dominante entre los economistas es que el salario
mínimo es una distorsión de mercado que, de tener
efectos, causa desempleo o informalidad y genera pérdidas de
eficiencia y bienestar social. Por lo menos, a nivel
microeconómico, tiene impactos opuestos sobre los ingresos
de los trabajadores, especialmente no calificados, y sobre las
ganancias de las empresas. Sin embargo, esta posición dista
de tener consenso, debido a que los salarios mínimos pueden
justificarse por razones de eficiencia o como una intervención
orientada a corregir fallas de mercado. De acuerdo con
diferentes estudios, el balance entre los beneficios del mayor
salario y el costo de las menores posibilidades de empleo
tiende a ser positivo y, por lo menos, en el corto plazo, los
aumentos del salario mínimo mejoran la distribución del
ingreso laboral (BID, 2004).”
468

469. 20. Discutir la afirmación que se hace en la clase
magistral: “Asumimos que las empresas operan
con rendimientos constantes o decrecientes a escala, que son las empresas típicas que pueden
habitar en competencia perfecta”. Es decir: ¿Por
qué una empresa con rendimientos crecientes a
escala podría no ser precio-aceptante?
R/ Una respuesta parcial es que una empresa con
rendimientos crecientes a escala, podría tener altos
costos fijos (por I+D y/o patentes, etc.), que le
harían tener algún poder de mercado (por
ejemplo, siendo monopolista, oligopolista, etc.).
469

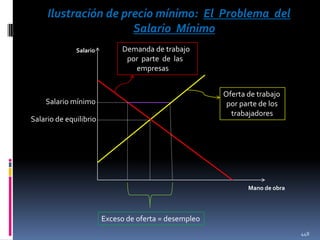
470. 21.
a) Dibujar en un diagrama de posibilidades de producción la
representación del cambio técnico (debido a una nueva invención)
de Y1=f(L,K) a Y2=1.1f(L,K). [Cabe advertir aquí que es usual recurrir al
coeficiente A en Y=Af(x,y) para medir el nivel de cambio tecnológico.]
b) Dibujar en un diagrama de posibilidades de producción, la
representación del cambio técnico (debido a un desastre natural) de
Y1=f(L,K) a Y2=0.8f(L,K).
K
L
470

471. 22. Aplicaciones elementales de la noción de
equilibrio parcial a la teoría del comercio internacional.
Precio
internacional
Oferta
Oferta
Exportaciones
Precio
interno
Precio
interno
Demanda
Precio
internacional
Importaciones
Demanda
Si el precio interno es
menor que el precio
internacional, el país
exportará.
Si el precio interno es
mayor que el precio
internacional, el país
importará.
471

472. Oferta
Oferta
Precio
interno
Precio
interno
Precio
Internacional
con arancel
Precio
internacional
Importaciones
Demanda
Importaciones
Precio
internacional
Demanda
La introducción de un arancel provoca un aumento del precio
internacional y una disminución de las importaciones
472

473. 23. (Falso o verdadero) “La introducción de un
arancel provoca una disminución del excedente
del consumidor y un aumento del excedente del
productor, pero este aumento, junto con los
ingresos recaudados por el Estado, no
compensan la disminución del excedente del
consumidor. En consecuencia, se produce una
pérdida de la eficiencia global de la economía.”
Sugerencia: Recurra a un gráfico como el anterior.
473

474. 24. Sabemos que una empresa competitiva y maximizadora
de beneficios contratará un factor hasta el punto en el que
el valor del producto marginal de ese factor (precio de
mercado del producto multiplicado por el producto
marginal del factor) sea igual a la retribución de ese factor.
a) En el caso del factor tierra, el valor de la productividad
marginal de la tierra deberá igualar a su alquiler:
p (productividad marginal de la tierra) = alquiler
b) En el caso del factor capital, el valor de la productividad
marginal del capital deberá igualar al tipo de interés
p (productividad marginal del capital) = tipo de interés (r)
474

475. 25. (*) “Debido a la reciente revaluación del peso
con respecto al dólar, el Ministerio de Comercio
decidió bajar aranceles a los bienes de capital
importados para que las empresas exportadoras
compren éstos y así disminuyan sus costos (El
Tiempo, Julio 25 de 2012)”. Discuta esta política
a la luz de lo aprendido en el curso.
475

476. 26) Imitando lo hecho en la clase
magistral, estudiar la incidencia de un impuesto
por cantidad vendida para distintas elasticidades
de la oferta.
27) a) Si la curva de demanda es vertical, la oferta
tiene pendiente positiva, y se impone un
impuesto de la forma Pd = Ps + t, ¿Cómo se
distribuye la carga impositiva?
b) Si la curva de oferta es vertical, la demanda
tiene pendiente negativa, y se impone un
impuesto de la forma Pd = Ps + t, ¿Cómo se
distribuye la carga impositiva?
28) Leer del texto de Varian intermedia
(2007, Antoni Bosch) desde el capítulo 14 hasta el
23, exceptuando el 17).
476

477. 29) Discusión sobre cuotas de producción.
30) Falso o verdadero:
a) “La inclusión de costos de transporte obliga a una
subida de la curva de oferta de un producto.”
b) “La inclusión de un centro de producción (es
decir, muchos productores de otra región) obliga a
que la curva de oferta se mueva a la derecha.”
31) A la luz de lo aprendido en clase, intente
explicar la existencia de bienes de precio cero
tales como los sistemas de software abiertos.
32) Describa, mediante gráficas de oferta y
demanda, el mercado de un bien que es ilegal
(por ejemplo, marihuana o cocaína).
477

478. 33) Discutir sobre el IPP (Índice de Precios al
Productor). Ver metodología del DANE.
478

479. CLASE MAGISTRAL #9
MONOPOLIO
479

480. Por definición, un monopolio es una estructura
de mercado de cierto producto homogéneo
(es decir, sin sustitutos “cercanos” y con
idénticos estándares), en el que solo hay un
vendedor y muchos compradores. Es una de
las “fallas de mercado” más estudiada
y, quizás, menos entendida.
El término “monopolio” proviene del griego
“mono”= único y “poleo”= vender, y su
primera referencia podría remontarse a
Aristóteles, aunque los monopolios han aparecido a lo largo de la historia desde la más
remota antigüedad.
480

481.  En la historia económica, los grandes mono-
polios surgieron a finales el siglo XIX con el
desarrollo de la revolución industrial y
comienzos de la era capitalista.
 Las razones principales de la existencia del
monopolio son las patentes (I+D), las licencias de exclusividad, los costos fijos y los
rendimientos crecientes a escala.
481

482. Existen, fundamentalmente, dos clases de monopolio:
i)
Monopolio legal (ordinario): Licencias otorgadas
(normalmente) por el Gobierno. Por ejemplo, la explotación
minera (petróleo, oro, carbón, etc.), las patentes, los
derechos de autor, etc. Aunque en ocasiones con altos costos
fijos, asumiremos aquí que estos operan con rendimientos
decrecientes (y en algunos casos especiales, constantes) a
escala.
ii) Monopolio Natural: Originado por las circunstancias o las
condiciones naturales. En general, operan con costos fijos
altos y rendimientos crecientes a escala. Por
ejemplo,
acueductos,
ferrocarriles,
redes
de
electricidad, gas, etc. Fue Thomas Malthus (1815) el primero
en reconocer, y J.S. Mill (1848) el primero en tratar, el
problema del monopolio natural.
En este curso no trataremos este último tipo de monopolio
debido a que, en general, trata con economías de escala, y
esto requiere un análisis particular con herramientas
formales más allá de los alcances de nuestro curso.
482

483. MOTIVACIÓN BÁSICA SOBRE LA EXISTENCIA DE UN MONOPOLIO
NATURAL
Si una empresa tiene dos plantas con funciones de costo C1(y1)= 3(y1)1/2 y
C2(y2)= 2(y2)1/2 (es decir, ambas con rendimientos crecientes a escala)
entonces el productor producirá en la planta menos costosa, pues debe
resolverse
Minimizar C1 (y1)+C2(y2) sujeta a y1 + y2= Y
y2
•
Producir todo
en la planta 2
que es la menos costosa
y1+y2=Y
y1
483

484. Asumiremos entonces (con algunas excepciones), que nuestro monopolista es de tipo
legal (u ordinario), y que, aunque está en capacidad de colocar el precio de venta de su
producto, también enfrenta un mercado
competitivo de insumos y, por lo tanto, su
función de costos se calcula de la misma
forma que lo hemos hecho para la empresa
competitiva.
484

485. El Problema Básico del Monopolio Legal
Maximizar p y – c(y)
con la condición de que
p = p(y)
(función inversa de demanda)
Asumiendo que c(y) es convexa estricta, es
decir, que la tecnología trabaja con rendimientos
decrecientes a escala, entonces arribamos a que
la condición de primer orden es:
485

486. p(y) + y p’(y) = c’(y)
Ingreso marginal
costo marginal
De donde se desprende (con p’(y)= dp/dy) que:
p(y)[ 1 + (dp/dy)/(p(y)/y) ] = c’(y)
Y así,
p(y)[ 1 + 1/ε(y)] = c’(y)
Ecuación de equilibrio
del monopolista
donde ε(y) = (dy/dp)/(y/p) es la elasticidad-precio
de la demanda del producto.
486

487. Ahora: en equilibrio, la elasticidad-precio de la demanda
ε(y) en el problema del monopolista es menor que -1, pues
si -1 ≤ ε(y) <0, el ingreso marginal
p(y)[ 1 + 1/ε(y)]
sería menor que, o igual a cero, y no podría ser igual al
costo marginal, que es mayor que cero. Es decir, ¡para
maximizar el beneficio, un monopolista (legal) siempre
opera en la parte elástica de la curva de demanda! Es
decir, en la parte “más sensible” a los precios de la curva
de demanda. Esto debido a que en la parte inelástica de la
curva de demanda, el ingreso marginal es negativo.
487

488. Además,
<1
c´(y) = p(y)[ 1 + 1/ε(y)] < p(y)
Y así, en equilibrio del monopolista:
c’(y) < p(y)
Es decir, al maximizar el beneficio, el monopolista coloca
cantidades de su producto en el mercado a un precio
superior que su costo marginal y, por lo tanto, superior al
precio de competencia perfecta. El problema aquí radica
en que, entonces, no todos podrán acceder a ese bien o
servicio.
488

489. Equilibrio de un Monopolista Legal
Zona elástica
de la demanda
Costo marginal = c´(y)
p
Solución del
monopolista
Demanda = p(y)
pm
•
•
ym
Ingreso marginal = p(y) + y p’(y)
= p(y) (1 + 1/ε)
y
Nota: Observemos que la curva de ingreso marginal p(y) + y p’(y) es igual a p(y) cuando y=0;
y, dado que y p’(y)≤ 0 entonces siempre está “por debajo” de la curva de demanda.
Además, asumimos que la curva de ingreso marginal tiene pendiente negativa, es
decir, que (p(y) +y p’(y))’ = 2p’(y) + yp’’(y) <0. Una forma de garantizar esto es que
tengamos la curva de demanda recta (p’’=0), o bien que la curva de demanda no sea
“muy convexa”.
489

490. Beneficio (de corto plazo)de un Monopolista Legal
Solución del
monopolista
Costo medio (corto plazo): tiene la
misma forma que en competencia
perfecta (¿por qué?)
Costo marginal
(oferta de corto plazo)
•
pm= Precio del monopolista
Beneficio del
monopolista
Demanda
(Ingreso medio)
Costo medio del monopolista
ym
Ingreso marginal
490

491. Posible beneficio negativo (de corto plazo) de
un monopolista
Solución del
monopolista
Pérdidas
pm= Precio del monopolista
•
Costo medio (corto plazo)
Costo marginal
(oferta)
Demanda
(Ingreso medio)
ym
Ingreso marginal
Note que el precio competitivo también arroja pérdidas
491

492. Análisis de Excedentes bajo Monopolio Legal
p
Excedente del
consumidor
Pérdida
irrecuperable
Costo marginal
(oferta)
pm
pc
Demanda
Excedente
del productor
ym
yc
y
Ingreso marginal
492

493. 1. ¿Por
qué cuando el monopolista tiene
pérdidas aún puede tener un surplus positivo?
Respuesta: Porque el surplus es una medida
de la eficiencia económica del monopolista
(maximización del beneficio) y no de si ese
beneficio es (o no) positivo. Además, sabemos, el
surplus es igual al beneficio más los costos fijos.
2.
Y si un monopolista va a obtener pérdidas…¿entonces por qué y cómo opera?
493

494. Regulación del monopolista con beneficio
negativo mediante precios tipo Ramsey
Solución del
monopolista
pR= Precio Ramsey (regulado)
Costo medio
(corto plazo)
∙
Pérdidas
pm= Precio del monopolista
•
Costo marginal
(oferta de corto plazo)
Demanda
(Ingreso medio)
yR
ym
Ingreso marginal
1. Note que también el precio competitivo arroja pérdidas.
2. El precio Ramsey (precio donde Demanda = Costo Medio) arroja
ganancias nulas.
494

495. Ejemplo sencillo de monopolio
Un monopolista con una función de costos C(y) = y2 se enfrenta a la
curva de demanda y = 12 - p. ¿Qué precio fijará y qué cantidad venderá ?
Ingreso marginal
Costo marginal
Y así,
p
Costo marginal
12 •
Costo medio
•
p* =9
ganancias
Solución
El problema es:
Maximizar Π = (12-y)(y) - y2
que nos lleva a
12- 2y = 2y
Ingreso marginal
3
y*=3 6
y* = 3 ,
Por lo tanto,
p* = 9
Π* = 18
Demanda
12
y
Notemos que el punto (3,9) está en la
parte elástica de la curva de demanda:
En efecto, la elasticidad-precio de la
demanda allí es:
ε = (dy/dp) / (y/p)= -1 / (y*/p*)= -3 < -1
495

496. El ejemplo anterior en competencia perfecta
En este caso el problema es
Maximizar py –y2
lo que nos lleva a que la curva
de oferta es
y=p/2
Y así, al igualar ésta a la demanda,
obtenemos
p/2= 12 –p
p=Costo marginal
p
(Curva de oferta)
12 •
Costo medio
•
p =8
Ganancias
Ingreso marginal
¿por qué es constante?
4
ó
p*= 8
Y así,
y=4
12
y
y*= 4
Demanda
y
π = p y* – (y*)2 = 16
496

497. Comparación de excedentes en monopolio y
competencia perfecta
p
p
12
12
p=costo marginal
(Curva de oferta)
Costo medio
pm= 9
pCP=8
pCP =8
•
6
Ingreso marginal
12
y m =3
y
yc=4
12
y
Demanda
Excedente
del
consumidor
=4.5
Excedente del
productor
= 18
Pérdida
irrecuperable
= 1.5
Excedente del
consumidor
=8
Excedente del
productor
= 16
497

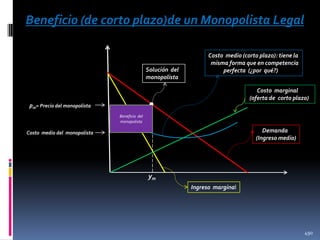
498. Otro ejemplo sencillo de monopolio
Supongamos que la curva de demanda que enfrenta un
monopolista es y = 1/pα (α>1) y que el costo marginal es c (constante). Entonces la ecuación de equilibrio
del monopolista es
p (1 + 1/ε) = c
Pero como ε = -α, entonces
p= c / (1 - 1/ α) = [1 + 1 / (α-1)] c
498

499. En este caso se afirma que el precio tiene un mark-up constante sobre el costo marginal. Es decir, el mark-up (margen) del monopolista mide la diferencia entre el precio y
el costo marginal y, en este caso, esa diferencia es
[1 / (α-1)] c. Notemos que mientras más elástica sea la curva
de demanda (y, por lo tanto, más cercana a la curva de
ingreso marginal competitiva (horizontal)), menor será el
mark-up, y más cercano será el precio monopolista del
precio competitivo.
En ocasiones, se recurre al mark-up como “medida de concentración del monopolio”. Otra de estas medidas es el
“ratio de concentración” que es la participación de las 3 ó 4
empresas más grandes del sector.
499

500. El índice de Lerner (Abba Lerner (1903-1982)) es un indicador del
poder de monopolio basado en el mark-up: A partir de la igualdad
de equilibrio monopólico
pm (1 + 1/ε) = c
se define este índice así:
IL ≡ (pm – c)/pm = -1/ε (< 1 )
Es decir, se define como el (negativo del ) inverso de la
elasticidad de la
demanda en el punto precioproducción monopólico.
Note que si
ε
es
grande, entonces el precio monopólico es muy cercano
al competitivo. Es decir, si IL =0 estamos en competencia
perfecta; mientras que si IL es muy cercano a 1, el mercado
enfrenta un mayor poder monopólico de esta empresa. En
nuestro ejemplo, como ε = -α, entonces la curvatura de la
demanda determinará qué tan competitivo es el precio de la
firma.
500

501. REGULACIÓN DEL MONOPOLIO LEGAL CON
SUBSIDIOS
Demanda regulada
(línea quebrada)
Excedente del
productor
Excedente del
consumidor
Costo marginal
(oferta)
pm
pcp
Ingreso marginal
Pérdida
irrecuperable
ym
ycp
Demanda
501

502. Algunas prácticas del monopolista
1. Discriminación de precios de primer, segundo
y tercer grado.
2. Barreras a la entrada: Fijación depredadora
de los precios, exceso de capacidad y fijación
de precio límite.
502

503. DISCRIMINACIÓN DE PRECIOS
“Discriminar precios” significa cobrar precios distintos a cada
cliente o a cada mercado. Ejemplos de ello, son las líneas aéreas
que tienen el monopolio de una determinada ruta: pueden cobrarle
una tarifa más alta a los clientes que viajan por negocios (pues éstos
no tienen más remedio que viajar) que a los que van de vacaciones
(pues éstos pueden tener otras alternativas). Con estas prácticas, el
monopolista obtiene más beneficios que si cobrara un único precio
en el mercado. Por ello, los vuelos de temprano en la mañana y a
horas altas en la tarde de días regulares, son, normalmente, los más
costosos.
503

504. El economista británico A.C. Pigou (1920) clasificó este fenómeno en tres tipos:

Discriminación de primer grado, que consiste en aplicarle al comprador el
máximo precio que esté dispuesto a pagar por unidad del bien. Aquí se incluyen
negociaciones (y regateos) sobre el precio del bien. Un médico rural es un caso
típico.

Discriminación de segundo grado (o colocación de precios no-lineales
(nonlinear pricing), que consiste en aplicarle al comprador un precio diferente
dependiendo del número de unidades que compre. Por ejemplo, compras en
grandes cantidades, la factura telefónica.

Discriminación de tercer grado, que consiste en aplicarle distintos precios a
distintos compradores. Por ejemplo, promociones tipo “Descuento para los que
cumplan años”; “Los viernes, el aperitivo es gratis para mayores de 60 años”;
“Happy Hour”; etc. Una compañía de teléfonos que cobra diferentes tarifas por
llamadas durante el día o la noche es un buen ejemplo de esta discriminación de
precios. La razón de que los precios sean más altos durante el día es que la
demanda es rígida: algunas llamadas telefónicas tienen que realizarse en
horario laboral.
504

505. Un ejemplo sencillo de
discriminación de tercer grado
Un vendedor monopolista tiene dos tipos de compradores, tipo
1 y tipo 2. Las curvas de demanda correspondientes son
p1= 2 –3y1, p2= 1 – 2y2; y la función de costos es C(Y)= Y2 ,
Y=y1+y2. Entonces el vendedor maximizará su beneficio
π = p1 y 1 +p2 y 2 – (y1+y2)2 = (2-3y1)y1 + (1-2y2)y2 – (y1+y2)2
y obtendrá, derivando con respecto a y1 y y2 , e igualando a
cero:
1- 4y1-y2= 0;
1-6y2-2y1=0
Resolviendo simultáneamente, obtenemos que:
y*2= 2/22, y*1=5/22 y así
p*1= 29/22 , p*2= 18/22
505

506. Por lo tanto, le cobra menos al comprador de primer tipo
que al de segundo tipo. Pero…¿por qué? La clave está en
las elasticidades-precio de la demanda, es decir, le
cobrará más al que tenga menor elasticidad (en valor
absoluto) o, lo que es lo mismo, al tipo de comprador que
sea “menos sensible” a un cambio de precios. En
efecto, la elasticidad-precio de la demanda del tipo 1 es
- [p1/ (2-p1)] = - 29/15
y la elasticidad-precio de la demanda del tipo 2 es
- [p2/(1-p2)] = - 9/2
El beneficio que obtiene el monopolista es
π*= p1 y 1 +p2y 2 – (y1+y2)2 = 0.2973
506

507. Si el monopolista no discrimina, entonces el problema será
Maximizar p Y(p) – Y2(p)
donde Y= y1(p) + y2(p). Es decir,
Maximizar
p[7/6 – 5p/6] - [7/6 – 5p/6]2
Derivando con respecto a p e igualando a cero, obtenemos
que:
p* = 22.4 / 22 ,
Y* = y1 + y2 = 0.318
Y el beneficio será π= p Y* – (Y*)2= 0.223. Así, el beneficio
será mayor si el monopolista discrimina (π =0.2973) que
si no discrimina (π =0.223).
507

508. Discriminación versus No-Discriminación
p1
p2
p
29/22
22.4 / 22
18/22
y1
El monopolista discrimina entre dos tipos
de consumidores
y2
Y=y1+y2
El monopolista no
discrimina
508

509. BARRERAS A LA ENTRADA
Muchas empresas, cuya posición monopolística
inicial posiblemente tuvo su origen en alguna
innovación o patente tecnológica, consiguen
conservar su posición dominante, al menos
durante un tiempo, aún después de haber
expirado las patentes (Kodak, IBM, Polaroid).
509

510. Los tres casos típicos de barreras a la entrada
son:
 i) Fijación depredadora de los precios: bajar los
precios radicalmente (inclusive por debajo del
costo de producción de la nueva empresa) para que
las empresas
competidoras no obtengan
beneficios de la entrada, o
que, si han
entrado, acaben quebrando. Una de estas figuras
es el dumping, que es ilegal en muchos casos pero
difícil de demostrar.
ii) Exceso de capacidad: Construir instalaciones
productivas mayores de lo que es necesario, como
señal de que la empresa ya existente está
dispuesta a una feroz competencia de precios y
que puede hacerlo.
510

511. iii) Fijación de precio límite: Una empresa que esté
considerando la posibilidad de entrar al mercado de un
monopolista, sabe qué precio se cobra en el mercado y
tiene una idea exacta de cuáles son sus propios costos de
producción, pero quizás no de los costos de producción
del monopolista. Así, éste puede tratar de engañarlo
haciendo pensar al potencial competidor de que sus costos
son bajos (por ejemplo, al cobrar un precio inferior al
monopolístico que haga que el volumen de ventas aumente
y se vea como un negocio “próspero”) y que, por
tanto, podría ser rentable entrar en el mercado. Pero
luego de entrar, el competidor notará que ello no era
así, y acabaría quebrando. A tal precio inferior al
monopolístico se le conoce como “precio límite”.
iv) Costes irrecuperables: El monopolista hace una inversión
que no se puede recuperar si desea abandonar el mercado.
Esto aumenta el riesgo de entrada en el mercado.
511

512. Ejemplo Simple de Precio Límite
Ingreso marginal
Solución del
monopolista
p m= Precio del monopolista
•
Costo marginal
•
P L= Precio Límite
(Precio Ramsey)
Costo medio
Demanda
ym
y PL
Cualquier empresa que intente entrar en el mercado y producir una cantidad inferior a YPL tendrá
precio y costos medios mayores que los que está colocando ahora el monopolista y, por lo tanto, nadie le comprará. Y si intenta producir una cantidad mayor a YPL, tampoco podrá vender su
producción a un precio que cubra sus costos medios y tendrá pérdidas. Note que en YPL, el
monopolista baja el beneficio a cero. Note que se asume que la competencia es con la misma
tecnología.
512

513. El ejemplo anterior señala que, en el corto plazo, el
monopolista se comporta con curva de costo medio
descendente y, parecería estar produciendo con
rendimientos crecientes a escala, aunque ello no sea
así. De todas maneras, en este corto plazo, aplica
precios Ramsey que, en general, es una herramienta
para monopolistas multi-producto. Ellos son los
precios que maximizan el excedente del consumidor
sujetos a la restricción de que los ingresos de la firma
apenas cubran los costos. Y encontrarlos en empresas
multi-producto es difícil, como es el caso de empresas
de energía eléctrica que venden electricidad a diferentes horas del día y del año.
513

514. UNA BREVE APROXIMACIÓN AL PROBLEMA DEL
MONOPSONIO
Un monopsonista es un productor que es el único
comprador o demandante de un insumo (bien o
servicio). El término proviene del griego “mono”=
único y “psonio”= comprador.
Un ejemplo de esto lo vemos en la Federación Nacional de Cafeteros que es monopsonista de los productores de café en Colombia . Estos, por lo general, le
venden a la Federación a través de sus cooperativas
de caficultores.
514

515. También la demanda de cacao se concentra principalmente
en dos empresas, Luker y Compañía de Nacional de
Chocolates, quienes adquieren en promedio muy alto de
la producción nacional (84,4%), fundamentalmente a
través de comercializadores. Bajo estas condiciones, el
productor de cacao en Colombia enfrenta una estructura
de demanda prácticamente duopsónica, situación
similar a la que enfrentan los productores en el resto del
mundo. En efecto, si bien en Colombia la mayor parte
del cacao se destina al mercado doméstico, en otros
países como los africanos, que destinan casi la totalidad
de la producción a la exportación, los productores
enfrentan un oligopsonio en el eslabón de comercialización y procesamiento del cacao en el nivel
internacional.
Haremos enseguida un breve análisis del monopsonio
simple.
515

516. El monopsonista es un productor que tiene una función con rendimientos decrecientes a escala f(x) , donde x es la cantidad de insumos que compra al mercado
de manera única. Entonces , del mercado, toma como dada la curva de oferta del
insumo w= S(x) , y después maximiza el beneficio a la manera usual:
Maximizar p f(x) – w x
Bajo condiciones estándar sobre S(.), derivamos e igualamos a cero para obtener
que:
p f´(x)
Ingreso marginal
=
S(x) + x S’(x)
Costo marginal
Es decir, el ingreso marginal es igual al costo marginal, que difiere de la función de
oferta en el término positivo. Y esto lleva a que la cantidad demandada por el
monopsonista sea inferior a la cantidad en competencia perfecta, y que el precio que
paga es también inferior con respecto al precio competitivo, como observamos en
la gráfica siguiente:
516

517. Equilibrio del Monopsonista
Precio de compra = w
Costo marginal (=S(x) + x S’(x))
Curva de oferta (w = S(x))
w cp
w ms
•
•
x ms
x cp
Ingreso marginal (= p f´(x))
(curva de demanda)
Cantidad x (comprada
al mercado)
517

518. Comparación de excedentes entre el monopsonio y
la competencia perfecta
Competencia perfecta
Monopsonio
•
Excedente del
comprador
•
Excedente
del vendedor
Pérdida
irrecuperable
518

519. MONOPOLIO BILATERAL
Un monopolio bilateral es un mercado en donde
cohabitan un monopolio (u oligopolio) de oferta y un
monopsonio de demanda (u oligopsonio), y en dónde
tanto el vendedor como el comprador pueden influir
en los precios. Es decir, existe a la vez por parte de los
vendedores un monopolio (u oligopolio) y por parte de
los compradores un monopsonio (u oligopsonio). Pese
a abarcar las dos formas teóricas de monopolio puro y
monopsonio puro, son bastantes frecuentes pues
representan el intercambio de bienes que no son
comunes o corrientes (negociaciones).
519

520. COMENTARIOS FINALES SOBRE EL
MONOPOLIO
1. El mercado no consigue asignar en forma eficiente los
bienes cuando hay competencia imperfecta, lo cual
hace, por ejemplo, que los precios suban por encima
del costo marginal y que las compras de los
consumidores, por efectos del precio, se reduzcan
hasta niveles ineficientes, lo que genera niveles de
desigualdad en la renta y en el consumo y una
distribución inequitativa de todos los bienes. Para
luchar contra esta situación, algunos consideran
necesaria la intervención del Estado.
520

521. 2. En los últimos años los gobiernos han tomado
medidas
para
frenar
el
poder
del
monopolio,
aprobando
leyes
antimonopolio, regulando sus beneficios, o
prohibiendo algunas prácticas de los mismos. Así
mismo, los gobiernos intervienen a través de la
regulación de los precios, fija y recauda impuestos
por las rentas recibidas por la posesión de los
diversos factores de producción, regula la oferta
monetaria y las condiciones crediticias para
fomentar el crecimiento económico y la productividad y controlar la inflación y el desempleo de
acuerdo con las condiciones macroeconómicas de
cada país.
521

522. 3. Las leyes sobre competencia pueden tener
varios objetivos generales: la promoción y
defensa de la competencia, la promoción de la
eficiencia económica y el bienestar de los
consumidores, la libertad de iniciativa, la
apertura de los mercados, la participación justa
y equitativa de medianas y pequeñas empresas, la desconcentración de poder económico, y la prevención de monopolios y usos
indebidos de posiciones de dominio. A nivel
legal, 12 países occidentales, incluyendo a
Colombia, cuentan con legislaciones e instituciones que defienden la competencia.
522

523. En Colombia se encuentran: La Constitución Política de
1991 (Artículos 333 y 334), el Decreto Ley No. 2153 de
1992 por el cual se reestructura la Superintendencia de
Industria y Comercio, la Ley 1340 de 2009, el Decreto
No. 1302 de 1964 por el cual se reglamenta la Ley
155/59 sobre Prácticas Restrictivas Comerciales, la
Ley No. 155/59 de 1959 sobre Prácticas Restrictivas
Comerciales, la Decisión 285 de la Comisión del Acuerdo
de Cartagena Contentiva de las Normas para Prevenir
o Corregir las Distorsiones en la Competencia Generadas por Prácticas Restrictivas de la Libre Competencia.
523

524. El artículo 333 de la Constitución Nacional establece los principios de
libertad de empresa, libre competencia y libertad económica como
derechos radicados en cabeza de todos los ciudadanos y sometidos a los
límites que establezca la ley. La Constitución indica:
 "La actividad económica y la iniciativa privada son libres, dentro de los
límites del bien común. Nadie podrá exigir permisos previos ni
requisitos, sin autorización de la ley. La libre competencia es un derecho
de todos que supone responsabilidades. La empresa, como base del
desarrollo, tiene una función social que implica obligaciones. El Estado
fortalecerá las organizaciones solidarias y estimulará el desarrollo
empresarial. El Estado, por mandato de la ley, impedirá que se obstruya
o se restrinja la libertad económica y evitará o controlará cualquier
abuso que personas o empresas hagan de su posición dominante en el
mercado nacional.
 "La ley delimitará el alcance de la libertad económica cuando así lo
exijan el interés social, el ambiente y el patrimonio cultural de la
nación."
524

525. Tareas para la clase con el profesor
asistente
De los siguientes ejercicios, hacer: 1, 2, 3, 4
y 7. Y, por supuesto, el profesor titular y
los profesores auxiliares estamos en
dispo-sición de aclarar las dudas que
surjan al realizar los otros ejercicios.
525

526. 1. Muestre,
en el problema del monopolista
legal, que el ingreso marginal I’(x) es igual a
I’(x)=p(1+1/ε) donde ε es la elasticidad-precio de la
demanda. Así, ε=-1 si, y solo si, I’(x)=0; ε<-1 si, y
solo si, I’(x)>0; ε>-1 si, y sólo si, I’(x)<0. Ilustre esto con
una gráfica apropiada.
2. Un monopolista presenta una función de costos
marginales constantes e iguales a $5 y enfrenta la
demanda de mercado Q=53–P.Determine el equilibrio
de mercado (cantidad, precio y utilidades del
monopolio). Grafique la pérdida irrecuperable del
monopolio.
526

527. 3. Suponga que una única empresa produce
cigarrillos y que el coste marginal de
producirlos es constante. Suponga que se
establece un impuesto de $100 sobre cada
paquete de cigarrillos. Si la curva de demanda
de cigarrillos es lineal, ¿subirá el precio en una
cuantía superior o inferior a la del impuesto?
[Sugerencia: Asuma c’(y)=c , p =a - by + 100,
π =(a–by+100)y - cy. Si π’ =0 entonces y*=
(a-c+100)/2b. Así, p*=(a+c)/2+ 50. Por lo
tanto, sube el precio en una cuantía inferior a la
del impuesto.]
527

528. 4. La demanda de un producto está dada por Q= 250(P/2). El bien es producido por una empresa cuyo costo
total está dado por CT= 200 + 20Q + 5Q2 . Calcule la
cantidad y el precio de equilibrio si el competidor actúa
como monopolista.
5. Una empresa produce bajo la función de producción
Q=6K0.5L0.5 y enfrenta la demanda de mercado
Q=100-5p, y paga precios de insumos por unidad de
wL=18, wK=8. Calcule el precio y la cantidad de equilibrio
si actúa como un monopolista.
6. Una empresa tiene un costo variable medio constante de
$5. La empresa estima su curva de demanda en P = 24 0.027Y. Su costo fijo es de $1,700. Si le consultaran a
usted, ¿qué precio recomendaría? ¿Cuánto beneficio se
espera que alcance la empresa?
528

529. 7. Si las funciones de costo total y de demanda (en
dólares) son, respectivamente, CT(Q) = 50 + 15Q +
Q2/100; P = 215,4 - 5Q, indique el precio y la cantidad de equilibrio, en los siguientes casos:
a) La empresa se comporta como una industria perfectamente competitiva.
b) La empresa se comporta como un monopolio maximizador de beneficios.
c) La empresa se comporta como un maximizador de
ventas sujeto a una restricción de generar un beneficio de $1,933.
8. Hacer una pequeña nota sobre la Escala Mínima
Eficiente del costo medio y su relación con el tipo de
competencia en el mercado (competitiva, monopolista, etc.).
529

530. 9. Un monopsonista tiene una función con rendimientos
decrecientes a escala f(x) = x1/2 , donde x es la cantidad de
insumos que compra al mercado de manera única. Del
mercado toma como dada la curva de oferta del insumo w=
S(x)=5x2 . Encuentre la cantidad comprada por el monopsonista y el precio por unidad al que compra.
10. Un vendedor monopolista tiene dos tipos de
compradores, tipo 1 y tipo 2. Las curvas de demanda
correspondientes son p1= 7-2y1, p2= 4-y2; y la función de
costos es C(Y)= Y2 , Y=y1+y2. ¿Le convendrá (en términos
de maximizar beneficios) a este monopolista discriminar
precios entre los compradores?
11. Presentar el problema de las tarifas de dos tramos.
530

531. CLASE MAGISTRAL # 10
OLIGOPOLIO
Y
COMPETENCIA MONOPOLÍSTICA
531

532. DUOPOLIO
Por definición, un duopolio es una estructura de
mercado de cierto producto homogéneo (sin
sustitutos “cercanos”), en el que sólo hay dos
vendedores y muchos compradores. Es una “falla
de mercado” muy estudiada y, quizás, mejor
entendida que el monopolio.
El término “duopolio” proviene del griego (“duo”=
dos, “poleo”= vendedor) y su primera referencia
formal se remonta a Augustin Cournot
(1838), aunque, obviamente, esta estructura de
mercado ha aparecido, aquí y allá, desde tiempos
remotos en la antigüedad.
532

533. El Problema Básico del Duopolio Cournot
El modelo básico de Cournot sobre esta estructura
de mercado presenta dos empresas, 1 y 2, que
producen un mismo bien homogéneo (cemento, cubos
de caldo de gallina, azúcar, etc.) con costos marginales constantes (c >0), y que enfrentan una
cur-va de demanda de la forma p= a- (y1+y2) donde
y1 es la producción de la empresa 1 y y2 es la producción de la empresa 2. Asumiremos aquí que a >
c; es decir, que el precio inicial de mercado es mayor
que el costo marginal, que es el mismo que el costo
de la primera unidad de producción.
533

534. Toda la información anterior la saben ambos
productores. Ahora: si ellos se involucran en una
competencia por maximizar sus beneficios, ¿qué
precio de mercado colocarán, y qué cantidades del
producto pondrán cada uno en el mercado? Inicialmente, cada una intentará maximizar sus beneficios:
Π1 = py1-cy1 = (a-(y1+y2))y1 – c y1 (1)
Π2 = py2-cy2 = (a-(y1+y2))y2 – c y2 (2)
534

535. Derivando π1 con respecto a y1 e igualando a cero,
obtenemos
a - 2y1 - y2 – c =0
Y así,
y1 = (a - c - y2)/2
(Curva de reacción de 1)
(3)
Entonces la empresa 1 nota que la maximización
de su beneficio no depende de sí misma y del
mercado, sino que también depende de la
producción y2 que coloque su competidor en el
mercado.
535

536. Por su parte, la empresa 2 debe haber hecho lo mismo:
Deriva π2 con respecto a y2 e iguala a cero, obteniendo
a - 2y2 - y1 – c = 0
Y así obtiene que:
y2 = (a-y1 - c)/2 (Curva de reacción de 2)
(4)
Obviamente, la empresa 2 también nota que la
maximización de su beneficio no dependerá de sí
misma y del mercado, sino que también dependerá
de la producción y1 que coloque su competidor en
el mercado.
536

537. Así las cosas, la empresa 1 va a incorporar la
producción óptima de la empresa 2 dentro de
sus cálculos, es decir, toma la ecuación (4) y la
incorpora en su ecuación de producción óptima
(3):
y1 = (a – c – y2)/2
= [a – c – [(a – c – y1)/2 ]/2
Y despejando obtiene que:
y1* = (a-c)/3
(5)
537

538. Pero como la empresa 2 debió haber hecho el
mismo cálculo, entonces, por simetría, también
va a obtener:
y2*= (a-c)/3
(6)
Y así, a estas cantidades, el precio de equilibrio
de mercado será:
p= a –(y1+y2) = a –(2(a-c)/3)
O bien,
p*= (a+2c)/3
(7)
538

539. Y el beneficio (que es el mismo para ambos, por
simetría) será:
Π = (a-(y1+y2))y1 – cy1
= (a-c) 2/9
Lo primero que se nota es que el precio de equilibrio de este duopolio es mayor que el costo marginal:
p*= (a+2c)/3 > c
pues, por hipótesis, a > c. Y, por lo tanto, debe haber ineficiencia. Veamos esto.
539

540. Duopolio Cournot versus Equilibrio Competitivo
P
a
Costo marginal = c
Excedente
del consumidor
Pd=(a+2c)/3
Demanda agregada
P = a-Y
Excedente
del productor
Pcp=c
Ingreso marginal
de los duopolistas
(Img=a-(3/2)Y)
Yd=
Y cp=
2(a-c)/3 a-c
Y=y1+y2
(Producción
agregada)
540

541. Estabilidad del equilibrio de Cournot
y2
y1 = (a-c-y2)/2
(Curva de reacción de 1)
Equilibrio
de Cournot
•
y2 = (a-c-y1)/2 (Curva de reacción de 2)
y1
541

542. ¿Y qué tal si los duopolistas se repartieran la
cantidad monopolista en partes iguales? Es
decir, ¿será posible que los productores hagan
colusión en un cartel? Veamos:
La función de beneficios es, en ese caso,
Πm = p y – c y = (a – y) y – c y
Derivando e igualando a cero, obtenemos:
y m= (a - c)/2 y así
pm = (a + c)/2
542

543. La colusión en cartel consistiría, en este caso,
que ambas empresas produjeran la mitad de la
cantidad de monopolio:
ym /2= (a – c)/4
Obteniendo, ambos , un beneficio
Π = p (ym/2) – c (ym/2) = (p - c) (ym/2)
= ((a + c)/2 - c)((a-c)/4)
= (a – c)2 / 8 = Π
543

544. Duopolio Cournot versus Monopolio
P
Ingreso marginal
del monopolista
(P= a- 2Y)
a
Costo marginal = c
Pm=(a+c)/2
Demanda P = a-Y
PCournot=(a+2c)/3
Pcp= c
Ingreso marginal
de los duopolistas
(P=a-(3/2)Y)
•
Y m=
(a-c)/2
•
•
YCournot= Y cp=
a-c
2(a-c)/3
Y=y1+y2
544

545. Resumimos lo anterior en el siguiente juego:
Empresa 2
yd
Empresa 1
yd
ym /2
ym /2
(a-c)2/9 , (a-c)2/9
5(a-c)2/48 , 5(a-c)2/36
5(a-c)2/36 , 5(a-c)2/48
(a-c)2/8 ,
(a-c)2/8
O bien, haciendo (a-c)2=1 :
Empresa 2
yd
yd
Empresa 1
ym /2
0.111 ,
ym /2
0.111
0.104 , 0.138
0.138 ,
0.104
0.125 ,
0.125
545

546. Aquí notamos que, en este modelo estático, los
empresarios no alcanzan el acuerdo (colusión (o
pacto entre dos para hacerle daño a un tercero) en
un cartel) de dividirse la producción de monopolio, a pesar de que para ambos es mejor
con respecto al acuerdo de duopolio. Y esto
sucede porque si llegaran a ese acuerdo, entonces
ambos tendrían incentivos a cambiar de
estrategia unilateralmente, pues esto les da más
beneficios. Y como ninguno va a respetar el
pacto, entonces llegarán, nuevamente, a la
estrategia de duopolio.
546

547. DUOPOLIO STACKELBERG
En el caso del duopolio de Cournot, ambas empresas
compiten de manera simultánea, solo evaluando, cada
una, lo que la otra empresa podría hacer, e incorporando esa evaluación dentro de sus propios cálculos.
Ahora supongamos que la empresa 1 es “líder” y que
coloca primero una cantidad en el mercado (imagínense una empresa ya instalada en el mercado como
monopolista y que no puede evitar la entrada de un
competidor) a lo que la firma 2 (la “seguidora”),
sabiendo esta cantidad, va a responder colocando otra
cantidad. Veamos en detalle, qué sucede en este caso.
547

548. Heinrich von Stackelberg (1905 – 1946) propuso en
1934, en “Estructura de Mercado y Equilibrio”, un modelo parecido al de Cournot en sus fundamentales:
El precio de mercado es
p = a - y1 - y2
y las funciones de beneficio de ambas empresas son
Π1 = py1 – cy1 = (a –(y1+y2))y1 – cy1
Π2 = py2 – cy2 = (a –(y1+y2))y2 – cy2
(1)
(2)
548

549. Como la empresa 1 es la que coloca primero su cantidad en
el mercado, es muy probable que opere así: “Si yo coloco
la cantidad y1 en el mercado, ¿qué hará la empresa 2?”.
Dada la información que hay en este modelo, el empresario 1 puede hacer ese cálculo: toma la función de beneficios
del empresario 2 y la maximiza, derivando con respecto a
y2 e igualando a cero, para obtener que:
a – y1 – 2y2 – c = 0
Y así,
y2 = (a – c – y1)/2
Es decir, si el empresario 1 coloca en el mercado una
cantidad y1, el empresario 2 le colocará una cantidad
y2= (a-c-y1)/2.
549

550. Entonces, incorpora esta información dentro de su
función de utilidad
Π1 = (a –(y1+y2))y1 – cy1
= (a –(y1+[(a – c – y1)/2]))y1 – cy1
Y deriva (con respecto a y1) e iguala a cero, para
obtener su producción óptima:
y1* = (a – c)/2
Y así,
y2* = (a – c)/4
y
p* = a – y1* – y2* = (a+3c)/4
Y los pagos que reciben son
Π1= (a-c)2 / 8 ; Π2 = (a-c)2 /16
550

551. Ahora comparemos los tres modelos:
Cartel
Duopolio
Cournot
Duopolio
Stackelberg
Precio del
producto
(a+c)/2
(a+2c)/3
(a+3c)/4
Cantidad y1
(a-c)/4
(a-c)/3
(a-c)/2
Cantidad y2
(a-c)/4
(a-c)/3
(a-c)/4
Beneficio π1
(a-c)2/8
(a-c)2/ 9
(a-c)2/8
Beneficio π2
(a-c)2/8
(a-c)2/ 9
(a-c)2/16
551

552. P
a
Demanda del mercado
P = a-Y
PCartel= (a+c)/2
PCournot = (a+2c)/3
PStackelberg = (a+3c)/4
PCompetitivo = c
a
(1/2)(a-c)
2/3(a-c)
¾(a-c)
Y=y1+y2
a-c
Comparación entre las tres estructuras duopolistas
552

553. OLIGOPOLIO COURNOT
En este caso tenemos n empresas con el mismo costo marginal c, y además,
p = a - (y1+y2+y3+…+yn)
Por consiguiente, para cada i=1,2,…,n,
πi = pyi – cyi = (a – (y1+y2+y3+…+yn))yi – c yi
Y derivando e igualando a cero, obtenemos
la curva de reacción de la empresa i:
yi = (a – c – ∑j≠i yj )
i=1,2,…,n
Curva de mejor-respuesta
553

554. Si se resuelven simultáneamente estas n ecuaciones, se obtiene que cada una producirá
yi * = (a-c)/(n+1)
Y así,
p* = a – [n/(n+1)] (a-c)
Por lo tanto,
πi* = [(a-c)/(n+1)]2
554

555. Y haciendo n tender a ∞ (infinito), tendremos un
comportamiento similar al de competencia perfecta:
yi*=0,
p*=c,
πi*=0
Es decir, la producción individual nula (comparada
con la producción agregada de toda la economía; el
precio igual al costo marginal; y el beneficio individual nulo (comparado con el beneficio agregado de
toda la economía). Recordemos que en competencia perfecta, el aporte individual es insignificante
dentro de la operación agregada de toda la economía.
555

556. Sin embargo, esto no es más que consistencia
lógica interna del modelo. Si imaginamos 500
empresas del mercado operando de manera
oligopolista, donde cada una observa con
sumo cuidado a las 499 empresas competidoras, entenderemos que hay mucho de
irreal en el modelo de oligopolio con n
tendiendo a infinito.
556

557. P
a
Demanda del mercado
P = a-Y
P2-Cournot = (a+2c)/3
Pn-Cournot = (a+nc) /(n+1)
PCompetitivo = c
a
2/3(a-c)
(n/n+1)(a-c)
Y=y1+y2
a-c
Oligopolio â la Cournot cuando crece el número (n) de empresas
557

558. Noticia Portafolio (Agosto 27 de 2012)
De los 935.657 barriles por día que en promedio
se extrajeron en la primera mitad del año, un
total de 832.671, Ecopetrol y Pacific Rubiales
tuvieron una presencia de 558.665 barriles
por día (60%). El resto fue extraído por 8
empresas con menores participaciones (Occidental de Colombia, Petrominerales, Petrobras, entre otras).
558

559. COMPETENCIA
MONOPOLÍSTICA
Es una estructura de mercado que asume una gran
cantidad de consumidores y productores, pero menos
que en competencia perfecta (donde se asume que
existe una cantidad infinita de ambos tipos de
agentes). Ellos venden productos diferenciados mediante marcas, calidad, niveles de servicio, etc. No
hay barreras a la entrada y salida del mercado. Ejemplos de ello son la mayoría de negocios que vemos
en el comercio: peluquerías, bombas de gasolina,
na, charcuterías , misceláneas, librerías, almacenes de
artículos eléctricos, papelerías de barrio, etc.
559

560. UNA PRIMERA APROXIMACIÓN AL MERCADO BAJO
COMPETENCIA MONOPOLÍSTICA:
EL DUOPOLIO BERTRAND
Joseph Bertrand (1822-1900 ) en “Teoría de
la Riqueza (…)” de 1883, criticaba los modelos
de duopolio de Cournot (1838) por “irreal”, ya que
consideraba que la verdadera variable estratégica a estudiar era el precio y no las cantidades a
colocar por parte de las empresas. Al fin y al cabo, las cantidades no son un mecanismo efectivo
de mercado, como sí lo son los precios.
560

561. Recordemos, inicialmente, que los modelos de Cournot
y Stackelberg estudian mercados de duopolio para un
bien homogéneo (es decir, sin “sustitutos cercanos”).
El modelo inicial que planteaba Bertrand es para un
bien homogéneo también, pero esto resultaba ser poco
interesante: en cualquier momento, los compradores
demandarían de la empresa que les colocara el menor
precio. Entonces, por competencia, las empresas comenzarían alternativamente a bajar los precios hasta
colocar, ambas, el precio igual al costo medio mínimo,
(y, por tanto, igual al costo marginal)y esto las llevaría,
también a ambas, a un beneficio cero.
561

562. Para que el modelo fuera realmente interesante
(y más real) Bertrand entró a estudiar el mercado
duopólico de un bien “diferenciado” (por ejemplo,
el mismo bien físico, pero que se compra en lugares distintos). Asumiendo, por simplicidad, que el
costo marginal en ambas empresas es constante
c (es decir, producen con rendimientos constantes
a escala), y las cantidades que producen son
y1 = a - p1 + p2
y2 = a - p2 + p1
562

563. Los beneficios respectivos son:
π1 = p1y1-cy1= (p1-c)(a-p1+p2)
π2 = p2y2-cy2= (p2-c)(a+p1-p2)
Derivando π1 con respecto a p1, e igualando a cero; y después derivando π2 con respecto a p2, e igualando también a
cero, obtenemos las “mejor-respuestas”:
(a+p2+c)/2 = p1
(a+p1+c)/2 = p2
Y resolviendo simultáneamente, se obtiene que:
p1*=p2* = a + c (precio)
y1*=y2* = a (cantidad)
π1 = π2 = a2 (beneficio)
563

564. APROXIMACIÓN ESTÁNDAR AL MERCADO BAJO
COMPETENCIA MONOPOLÍSTICA
En el estudio de la competencia monopolística
estándar también se recurre a entenderlo como un
monopolio inicial o de corto plazo, es decir, antes de
que entren competidores. Y, una vez se observen las
ganancias de esta empresa, entrarán otros a
competirle hasta llevar los beneficios de la empresa
inicial a cero (es decir, beneficio cero en el “largo
plazo”). Es por esto que, ocasionalmente, se asimila
la noción de competencia monopolística a la de
“competencia”, pero sin coincidir con la noción de
competencia perfecta.
Algo notable de esta estructura es que, en el largo
plazo, al llevar los beneficios a cero por competencia, el resultado es similar a si cada competidor
actuara como un monopolista ordinario pero
enfrentando la demanda de largo plazo.
564

565. Comportamiento de corto plazo del competidor
monopolista
Solución del
competidor
monopolista
p cm= Precio del competidor
monopolista
Beneficio
del
competidor
monopolista
Costo medio (corto plazo)
Costo marginal
(oferta)
•
Demanda
(Ingreso medio)
de corto plazo
Costo medio del competidor
monopolista
Y cm
Ingreso marginal
565

566. Beneficio cero de largo plazo del competidor
monopolista
p
Solución del
competidor
monopolista
Costo medio
Costo marginal
(oferta)
p cm = Precio del competidor
monopolista
•
Demanda
(Ingreso medio)
de largo plazo
p cp = Precio de competencia
perfecta
ycm
Ingreso marginal
Ej.: p=a-ny
y
Note que el precio del competidor monopolista de largo plazo, no coincide con el de
competencia perfecta mostrando que la idea popular de que “la competencia baja los
precios” es cierta, mas no al nivel de eficiencia. La razón es que la entrada allí es de solo
unas cuantas empresas y no de “infinitas” como requiere la competencia perfecta. 566

567. Ejemplo
Una empresa de competencia monopolística se enfrenta a la siguiente función de demanda P=20 – nQ. La
función de costos de la empresa es CT= Q2 – 4 Q + 5.
a. Determinar su precio y el nivel de producción a corto
plazo. Evalúe si la empresa obtiene beneficios
económicos.
b. ¿Es posible la entrada de otras empresas al
mercado? Encuentre la solución de equilibrio para el
largo plazo.
Solución
a. En el corto plazo el competidor monopolista se
comporta como un monopolista y, por lo tanto, al
maximizar su función de beneficios, debe igualar el
ingreso marginal con el costo marginal. Es decir,
567

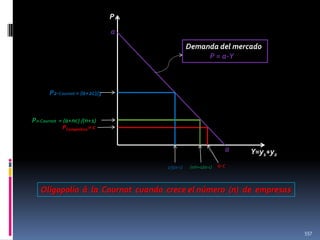
568. Img = d(PQ)/dQ = d[(20-Q)Q]/dQ = 20 – 2Q =
Cmg = d(CT)/dQ= d(Q2 – 4 Q + 5)/dQ = 2Q – 4
Y de allí, se tiene 20-2Q= 2Q-4, y, por tanto,
Q*= 6
Y así, de la función de demanda Q=20 – P, se obtiene
que
P*= 14
Y puesto que el costo medio (Cme= Q - 4 + (5/Q)) a
este nivel precio-producción es
Cme*= 17/6
Entonces esta empresa percibe un beneficio de
π = Q*(P* - Cme*) = 67
568

569. b) En el “largo plazo” buscamos inicialmente el
nivel de producción donde la tangente a la
curva de costo medio es igual a la pendiente
de la curva de demanda p= 20-nQ, donde
n=número de empresas competidoras);
es
decir, donde
1 - (5/Q2)= -n
lo que nos lleva, despejando, a que la
producción de largo plazo Q* está determinada por la igualdad:
Q* = √(5/n+1)
(1)
569

570. La condición de largo plazo de equilibrio monopolista
(ingreso marginal = costo marginal). Y así:
Im = d(PQ)/dQ = d[(20-nQ)Q]/dQ = 20 - 2nQ
= Cmg = 2Q-4
Lo que nos lleva a que (2n+2)Q = 24 y así
Q* = 12/(n+1)
(2)
Igualando las ecuaciones (1) y (2), obtenemos que
√(5/(n+1)) = 12/(n+1)
De donde
n=27,8
Y así,
Q* = 12/(n+1)=0,4166
y, por tanto,
P* = 20-(27,8)(0,4166) = 8,41
570

571. Ilustración del ejemplo del competidor monopolista
Corto plazo
Largo plazo
P
P
20
Cmg = 2Q -4
•
14
Cmg = 2Q -4
20
Cme = Q -4 + (5/Q)
8,41
Cme = Q – 4 + (5/Q)
∙
17/6
P = 20-Q
2.23
6
20
∙
Q
P = 20-(27,8)Q
0,41
Q
Img = 20 –(55,6)Q
Img = 20-2Q
Nótese la posibilidad de exceso de capacidad instalada
al pasar del corto plazo al largo plazo
571

572. Lo estudiado hasta ahora en esta curso es
una breve introducción a un área muy estudiada en la teoría económica: la ORGANIZACIÓN INDUSTRIAL. Es decir, la organización industrial estudia, básicamente, la
competencia perfecta e imperfecta en mercados de diversa índole.
572

573. Tareas para desarrollar con el profesor
asistente
1. El mercado de los tufis de un país muy lejano está formado por dos
firmas, A y B , cuyas funciones de costo son idénticas e iguales a
C(q)= a + c q. La función de demanda por tufis en este mercado es
Q(P)= d-P, donde d > a > c > 0. Dados los siguientes escenarios:
i) Ambas firmas compiten de acuerdo al modelo de Cournot.
ii) Las firmas coluden.
iii) La firma A se comporta como líder, determinando la cantidad a
producir.
iv) La firma B se comporta como líder, determinando la cantidad a
producir.
Encuentre el equilibrio (precios y cantidades) en cada escenario y las
utilidades de las firmas.
573

574. 2. Un monopolista presenta una función de costos marginales constantes e
iguales a 5 y enfrenta la demanda de mercado Q = 53 – P. Determine el
equilibrio de mercado (cantidad, precio y utilidades del monopolio). Grafique el costo social del monopolio.
Debido a la alta demanda, una nueva firma logra entrar al mercado. Su
función de costos es la misma que la original. Suponga que las firmas se
comportan según un duopolio de Cournot, donde cada una maximiza sus
utilidades según lo que produce la otra firma.
a)Determine la función reacción de cada firma.
b) Determine cuál será la combinación de las cantidades producidas por
cada firma para la cual las expectativas de ambas se vean confirmadas
(equilibrio de Nash), determine el precio, cantidades y utilidades de cada
una.
574

575. 3. En el pequeño pueblo hay sólo tres productores de
escopetas, los cuales tienen función de costos (para
las tres la misma) C(q) = 5 + 5q. La demanda por
escopetas está representada por la función P = 30 –
Q. Suponga que se pueden producir “fracciones de
escopetas”.
a) ¿Cuál es el equilibrio si los tres productores deciden
producir simultáneamente y comportarse competitivamente según el modelo de Bertrand?
b) ¿Cuál es el equilibrio si los tres productores deciden
utilizar estrategias de Cournot?
575

576. 4. Considere un duopolio con la función inversa de
demanda P= 400 – 2Q donde Q es el total de la
cantidad producida por las dos empresas. La
empresa 1 tiene un costo marginal de 100 y la
empresa 2 tiene un costo marginal de 40. Calcule
las cantidades á la Cournot. Calcule el precio de
equilibrio. Calcule el beneficio de cada empresa.
5. Si CT1 = Q1 y CT2 = 5Q2 , encuentre el equilibrio a la
Bertrand con productos diferenciados si las funciones de demanda que enfrentan los duopolistas son
Q1 = 1000 – 20P1 + 15P2 y Q2 = 800 -15P2 + 5P1.
6. Llevar a cabo el estudio de excedentes de consumidor y
productor para la competencia Stackelberg y la competencia monopolística.
576

577. 7. Una empresa de competencia monopolística se
enfrenta a la siguiente función de demanda Q=30 –
P. La función de costos total de la empresa es CT=
Q2 – 3Q + 7.
a. Determinar su precio y el nivel de producción a corto
plazo.
b. Evalúe si la empresa obtiene beneficios
económicos.
c. ¿Es posible la entrada de otras empresas al
mercado?
d. Encuentre la solución de equilibrio para el largo
plazo.
8. Estudiar el modelo (simple) de competencia monopolística de Hotelling basado en la diferenciación
por localización.
577

578. 9. Estudiar el modelo Cournot en el que ambas empresas tienen
función de costos C(y) =y2 y con función de costos C(y) = y1/2.
10. ¿Por qué sí surgen los cárteles? Discutir brevemente el duopolio
como un juego repetido.
11. El oligopsonio es una estructura de mercado en
la que hay productores que son los únicos compradores de
un insumo ( bien o servicio) . Por ejemplo, en Colombia el bagazo de la caña de azúcar lo producen muchos
ingenios y sólo lo compran las pocas productoras de papel
del país. Plantear el problema que deben enfrentar dos
duopsonistas que compiten por cantidades de insumos.
12. ¿Si una tienda vende un producto que es proveído por
un monopolista, es él también un monopolista?
578

579. 13. Elaborar el diagrama de excedentes para la
competencia oligopolística á la Bertrand.
14. Estudiar el problema de un líder á la
Stackelberg, y dos seguidores que compiten á la
Cournot.
15. Leer del texto de Varian intermedia (2007, Antoni
Bosch) desde el capítulo 24 hasta el 28.
579

580. CLASE MAGISTRAL
# 11
OTRAS “FALLAS” DE MERCADO:
BREVE APROXIMACIÓN A LA TEORÍA
DE BIENES PÚBLICOS Y
EXTERNALIDADES
580

581. 1. Sobre Bienes Públicos Puros
Las dos características corrientemente asignadas a un bien público
puro son la no-rivalidad y la no-excluibilidad.
La primera significa que el hecho de que un agente disfrute del
bien, no reduce la cantidad de que pueden disfrutar los otros
agentes; y la segunda característica consiste en que ningún agente
puede ser excluido de su disfrute. Sin embargo, la definición
técnica más precisa de un bien público es la dada por Paul Samuelson (1954), en el que afirma que un bien público es un bien que,
una vez producido, puede ser disfrutado por un agente adicional
sin ningún costo !
581

582. Ejemplos de bienes públicos puros son: un parque
público, el aire fresco, un carretera pública, conciertos
al aire libre, el alumbrado público, la defensa nacional
y, también, en mi opinión, la educación pública.
Una parte sustancial de la teoría básica de los bienes
públicos está basada en los artículos de 1954 y 1958
de Paul Samuelson (1915-2009).
Estudiaremos aquí, un modelo simple de provisión de un
bien público puro mediante dos mecanismos: provisión
pública (Estado) y provisión privada (los mismos agentes).
Pero antes, distingamos la forma en que se construyen las
demandas agregadas cuando de un bien público se trata.
582

583. Ya sabemos que la demanda agregada de un
bien privado se calcula horizontalmente:
p
p
y1
Demanda agente 1
p
y2
Demanda agente 2
•
y1+y2
Demanda agregada
583

584. Pero la demanda agregada de un bien público se
calcula verticalmente:
Utilidad
marginal
del agente 1
Demanda agente 1
x0
y
Utilidad
marginal
del agente 2
Demanda agente 2
Utilidad
social
marginal
x0
Demanda agregada
x0
584

585. Ejemplo sencillo de provisión centralizada de un bien público:
maximizar el beneficio social menos el costo de producción
Utilidad marginal
= disposición a pagar
En X*, la suma (Ds) de las dos
disposiciones marginales a pagar =
costo marginal de provisión.
Ds = 2D1
•
Costo marginal
D1
X*
Nivel de provisión
X* = provisión eficiente del bien público; pero no necesariamente proveído por
incentivos individuales: los dos querrán ser “polizones” (free-riders)
585

586. Ejemplo sencillo de provisión privada de un bien público: No
hay suficientes incentivos!
Di = Utilidad marginal de i
= disposición a pagar de i
En X**, disposición marginal
a pagar del agente 1 = costo
marginal
Ds = 2D1
•
Costo marginal
D1
•
X**
X*
X
X**= provisión del bien público por parte de un solo individuo; el otro es “polizón”
(free-rider). Note que X** < X* (sub-provisión)
586

587. Financiación por impuestos
Los individuos no compran bienes públicos (los pueden disfrutar
igual si no pagan), luego el Estado debe financiarlos cobrándoles
impuestos a los individuos. Asumimos, de manera simplificada,
que el precio del bien público es la cantidad de impuestos que
tiene que pagar cada individuo.
Así, este individuo tiene una restricción presupuestaria:
τx+y= Y
La suma de lo que consume en bienes privados y lo que paga
como impuestos para comprar bienes públicos debe ser igual a su
renta.
587

588. El consumidor trata de obtener el máximo bienestar (utilidad) teniendo presente la restricción
presupuestaria.Y resolviendo ese problema, el
consumidor determina qué cantidad de bien pú-
blico que hace máximo su bienestar (en función
del precio). Esto lleva a la curva de demanda que no
es más que la disposición a pagar del individuo por
un bien.
588

589. Di = Utilidad marginal de i
= disposición a pagar de i
Ds = 2D1
τ
•
Costo marginal
D1
X*
X
589

590. Un ejemplo simplificado
Di =
=
Ds = demanda agregada de educación superior
Utilidad marginal de
cada estudiante
lo que paga cada
estudiante por
educación superior
Costo marginal
Con subsidio
a la demanda
τ
τ1
τ2
•
Con subsidio a
la oferta
Di = demanda individual por
educación superior
X*
τ2 = lo que paga cada estudiante con subsidio a la oferta
τ1 = lo que paga cada estudiante con subsidio a la demanda
τ = lo que paga cada estudiante sin estos subsidios
X=#estudiantes en
educación superior
pública
590

591. Teoría más general de bienes públicos puros
i) Provisión eficiente de dos bienes privados
(excluibles, rivales).
y
Curvas de nivel de
U(x,y)
Problema de la asignación
eficiente de bienes privados:
Maximizar U(x, y)
sujeta a F(x, y)= 0
•
Frontera de
posibilidades
de producción
x
La solución satisface:
∂U/∂x/ ∂U/∂y = ∂F/∂x / ∂U/∂y
591

592. ii) Provisión de un bien privado (x) y uno público (y)
(no-excluible, no-rival)
Supongamos dos agentes con funciones de utilidad
U1(x, y) y U2(x, y) donde x es un bien público y y es
un bien privado. Existe, además, una función de
producción entre x e y dada por F(x, y)=0.
El problema es:
Maximizar U1(x, y)
sujeta a U2(x, y) = constante
F(x, y) = 0
592

593. Condición de optimalidad entre un bien público y otro privado
∂F/∂x / ∂F/∂y = (∂U2/∂x / ∂U2/∂y) + (∂U1/∂x /∂U1/∂x)
Bien privado
a
F(x,y)=0
Consumo privado
del consumidor 1
U2(x, y) = constante
y2
b
Bien público
Bien privado
Curva de consumos
privados del consumidor 1
Pendiente de curva de nivel de
U1(x, y) = -∂U1/∂x /∂U1/∂y
•
y1
a
x1
b
Bien público
Pendiente consumo privado de 1 =
(-∂F/∂x / ∂F/∂y) - (-∂U2/∂x / ∂U2/∂y)
593

594. Ejemplo
Supongamos que las funciones de utilidad son
U1(x,y) = b1ln(x) + y
U2(x,y) = b2ln(x) + y
Y la frontera de posibilidades de producción es:
x+y = K
Así, la condición de optimalidad es:
1 = (b1/x) + (b2/x)
o bien:
x* = b1 + b2 (cantidad constante de bien público)
y1+ y2 = w
(restricción presupuestal con w constante)
594

595. Así, la cantidad de bien público que es eficiente producir es aquella cantidad en la
cual la cantidad de bien privado a la que hay
que renunciar para producir una unidad más
de bien público (tasa marginal de sustitución
técnica) es igual a la suma de lo que estarían
dispuestos a pagar los individuos (es decir, la
suma de las tasas marginales de sustitución).
595

596. Mecanismos para construir un bien público
Mecanismos de elección social; en particular, mecanismos
de votación (por ejemplo, la regla del votante medio).
ii) Impuestos Lindahl: precios personalizados.
iii) Mecanismos de revelación de la verdadera disposición a
pagar (información asimétrica). Por ejemplo, los mecanismos
de Vickrey (1961), Clarke (1971), Groves (1973). Note que los
individuos bajo información simétrica, revelan sus preferencias
sobre bienes privados, a través de “votos monetarios” (ofreciendo su dinero para comprar). Los individuos pueden no querer
revelar sus verdaderas disposiciones a pagar para poder pasar
por polizones.
iv) El análisis costo-beneficio.
i)
596

597. Ejemplo de mecanismo para la
construcción de una unidad de un bien público
Dos agentes, A y B, pueden construir un bien público que le
daría a cada uno un pago bruto de 20. Este bien público solo
puede construirse si entre los dos (A y B) reúnen 30 para su
construcción y, en ese caso, el pago neto sería de 20 menos la
contribución de cada agente. Suponga que el agente A dice
primero con cuánto va a contribuir y, después, el agente B
hace su contribución. Si la suma de las contribuciones es 30, el
bien público se construye; pero si está por debajo de 30, el bien
no se construirá y los dos agentes recibirán un pago de cero.
597

598. Una solución de este problema es:
El plan del agente B es que no contribuye si el agente
A contribuye con menos de 10; el agente B contribuye
con la diferencia entre 30 y la contribución de A, pero
si A contribuye con más o igual que 10. Sabiendo esto,
el plan del agente A será contribuir con 10.
Luego el agente B contribuirá con 20.
En efecto: En la primera etapa del juego, el agente A
escoge su contribución; viendo esto, en la segunda
etapa del juego, el agente B escoge su contribución.
598

599. El agente B optimiza en la segunda etapa del juego: Si el
agente A contribuye con menos de 10, el agente B no debe
contribuir, porque si lo hiciera tendría que ser con más de 20 para
construir el bien y esto le daría un pago neto negativo: por lo
tanto es mejor no contribuir y obtener 0 (cero). Si el agente A
contribuye con más que 10 entonces lo mejor que puede hacer el
agente B es contribuir con el resto que falta para completar 30,
pues si no lo hiciera obtendría 0 (cero) en lugar de 20 menos la
contribución, que le da un pago neto mayor que 0 (cero). Si el
agente A contribuye exactamente con 10, el agente B contribuye
con 20 y así el pago neto de B es cero. Este agente B podría
haber escogido no contribuir y también obtener 0 (cero); pero
ambas opciones son indiferentes para B, y escoge la de contribuir
con 20 si el agente A contribuye con 10.
599

600. El agente A optimiza en la primera etapa del
juego: Si el agente A asume que el agente B
optimizará de la manera anterior en la segunda
etapa del juego, el agente A, en la primera etapa,
escogerá contribuir con 10 porque sabe que, en
ese caso, el agente B estará entonces dispuesto a
contribuir con 20, y el pago neto del agente A será
de 10 (=20-10). Ninguna otra opción le da un mejor
pago neto al agente A.
600

601. 2. Sobre Externalidades
(Ver Notas sobre Micro I, UCLM)
Los “efectos externos” o “externalidades”, como
hoy se les llama, hacen su aparición en el “Principles
of Economics” (1890) de A. Marshall en la forma
de “economías externas”; es decir, economías
externas a una firma pero internas al mercado.
Pero fue A. C. Pigou (1877-1959) (el sucesor de
Marshall en Cambridge) quien, en su “Economics of
Welfare” (1920), desarrolló y extendió este concepto,
al ser una de las causas de la diferencia entre el
``producto neto privado'' y su “producto neto social” .
601

602. Los economistas definen una “externalidad” como
“una actividad de una de las partes, que entra
directamente en la función de utilidad o producción
de alguna otra de las partes en el mercado”. Sin
embargo, esta definición no es del todo satisfactoria
pues debemos reconocer que hay casos en los que la
influencia sobre la utilidad y los productos de otros, se
ejercen ``indirectamente'', es decir, vía precios; aunque
también hay casos, obviamente, en donde la influencia
se ejerce “directamente” sobre la utilidad y el producto.
602

603. Diremos que la externalidad y1 afecta al individuo
A, cuando la función de utilidad o de producción
de éste, toma la forma
fA = f A(x1,x2,...,xm ; y1)
donde x1, x2,...,xm son medidas de consumo o
producción que están exclusivamente bajo el
control de A; y donde y1 es una medida de
consumo o producción por parte de otro agente B.
603

604. Cuando cuando un aumento en la externalidad y1
implica un aumento en el bienestar o producción
del agente A, diremos que y1 es una “externalidad positiva” (o, en términos marshallianos,
que tenemos una “economía externa''). Y cuando
un aumento en la externalidad y1 implica una disminución en el bienestar del agente A, diremos
que y1 es una “externalidad negativa” (o una“diseconomía externa”).
604

605. Se asume que el agente A tratará de maximizar su utilidad de
la manera típica, pero sujeta a la externalidad y1. Esto lo
hará encontrando los valores de las x's, cuando y1 cambia, de
tal manera que alcance su equilibrio.
Como era de esperarse, una externalidad puede producir ineficiencias. Algunos de los métodos más conocidos que se
proponen corrientemente para ”corregir” externalidades
son la reasignación de los derechos de propiedad (Teorema de Coase (Ronald Coase (1910-)), la prohibición terminante, los impuestos y los subsidios, la regulación, los
acuerdos voluntarios y los mecanismos preventivos.
605

606. Algunos ejemplos específicos
Externalidades positivas
Externalidades en el
consumo
Externalidades en la
producción
Publicidad verdadera
I+D
Externalidades negativas
Ruido
Contaminación
606

607. Solo a manera de ejemplo de una externalidad
negativa, imaginemos una industria que produce
emisiones que contaminan el agua sin pagar sanción
alguna. Definimos el costo social marginal como
el costo marginal que tienen que soportar todos
los miembros de la economía, debido a la contaminación. Éste supera al costo privado marginal de la
empresa (que es el costo marginal que soporta sólo el
productor), en una cantidad que se llama costo
externo marginal.
607

608. Este costo externo marginal mide los costos marginales derivados de la contaminación por la actividad
productiva/ extractiva del productor. Y su estimación
se basa en la idea de que los costos externos de la
producción se reflejan en los cambios de, por
ejemplo, los precios de las actividades que afecta.
Para ello se requieren mecanismos de valoración
específicos que, normalmente, requieren de información apropiada y claridad sobre el valor de los bienes
afectados.
608

609. La función de bienestar social a optimizar es:
B(y) = BC(Y) - CS (y)
donde
CS(y) = CP(y) + CE(y)
BC(y)
CS(y)
CP(y)
CE(y)
= Beneficio de consumir y unidades
= Costo social de producir y unidades
= Costo privado de producir y unidades
= Costo externo al producir y unidades
609

610.  La condición de optimalidad es:
BCm g (y) = Cmg S (y)
que se lee:
“costo social marginal= beneficio marginal
de consumo”
Y que también puede escribirse como:
B Cm g (y) = CPmg S (y) + CEmg (y)
que se lee:
costo privado marginal más costo externo
marginal = beneficio marginal de consumo
610

611. Comportamiento de una empresa que produce
emisiones contaminantes
p
Costo social marginal
Costo marginal privado
Costo externo marginal
Curva de demanda de mercado
(beneficio marginal del
consumidor)
yext
ycp
y
El nivel de producción de acero (ycp) que genera externalidades negativas
es demasiado elevado en un libre mercado, con respecto al nivel eficiente (yext)
donde ya se ha incorporado la externalidad.
611

612. Para resolver este problema, normalmente se
recurre a intervención pública mediante tres
opciones:
Reasignación de los derechos de propiedad
(Teorema de Coase)
ii. La regulación
iii. Los impuestos (o subvenciones) pigouvianos
i.
612

613. i. Reasignación de los Derechos de Propiedad
(El Teorema de Coase)
La posibilidad de resolver los problemas que plantean
las externalidades reasignando los derechos de propiedad es una afirmación que se conoce como el Teorema de Coase (Ronald Coase (1910-)). El atractivo de
este teorema reside en que asigna un papel mínimo al
Estado, limitándolo a determinar quién tiene los derechos
de propiedad, y luego dejar que operen los mercados
privados.
613

614. Por ejemplo, si la empresa contaminante tuviera
derechos importantes sobre el río (es decir, derechos de propiedad sobre el agua limpia), controlaría las emisiones realizadas aguas arriba.
Sin embargo, este mecanismo de reasignar los
derechos de propiedad tiene problemas por ser,
en ocasiones, costoso por múltiples razones.
Todo esto hace que se requiera una intervención
más activa del Estado.
614

615. ii. La Regulación
Existen, básicamente, dos respuestas del
Estado al problema de la contaminación:
i) Prohibirla.
ii) Establecer límites de contaminación
con multas y sanciones.
615

616. iii. Los Impuestos Pigouvianos
En general, reducen de una manera más eficaz
las externalidades, que l a misma regulación, colocándole un precio al “derecho” de contaminar.
El mecanismo, en nuestro caso, de un monopolista
contaminador del agua, el Estado intenta maximizar
los excedentes del consumidor y del productor, y
minimizar el daño social producido por las emisiones.
616

617. Y aunque las matemáticas requeridas para este fin están
un tanto más allá de los prerrequisitos del curso, la fórmula utilizada para calcular el impuesto pigouviano es:
t* = tc - [P- Cmg] dy/ds
donde:
t c = dD/ds = cambio en la demanda (D) debido a un cambio de emisiones (s). A este lo llaman “el impuesto pigouviano cuando es una empresa competitiva”.
P = precio de monopolista
Cmg = costo marginal del monopolista
dy/ds = cambio en la producción (y) debido al cambio de
emisiones (s)
617

618. Cálculo del nivel eficiente de emisiones
Pesos por unidad
de emisión
Costo social marginal
Costo marginal de reducción
de emisiones
Nivel de emisiones
Nivel “eficiente” de
emisión
618

619. 25.00%
20.00%
15.00%
10.00%
5.00%
Emisiones totales de
dióxido de carbono en
el mundo (2009)
0.00%
619

620. Lo estudiado en esta clase magistral
es apenas una breve introducción a
un área muy estudiada en la teoría
económica: la ECONOMÍA PÚBLICA.
620

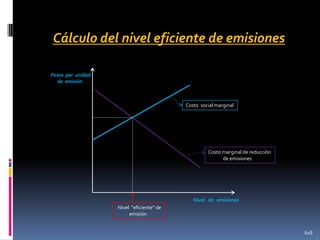
621. Tareas para desarrollar con el profesor
asistente
1. Calcular la óptima provisión de un bien público para
N individuos homogéneos (léase idénticos) con demanda individual Di(X)= a- bX, y donde el costo marginal
de proveer el bien público es Cmg(X)= c +dX. Después
haga n tender a infinito y calcule la provisión óptima e
interprete esto como el nivel de provisión de bien
público en el que el beneficio marginal (disposición a
pagar) de cualquier individual proveerse una unidad
adicional del bien público, es cero. [ Sugerencia: Igualar
nDi(X) con el costo marginal]
621

622. 2. Ahora trate el mismo problema anterior, pero
intentando que la provisión del bien público
sea privada. Luego compare este nivel de
provisión con el obtenido en el ejercicio anterior
y note que la de este ejercicio es menor. ¿Por
qué? [ Sugerencia: Igualar Di(X) con el costo
marginal]
3. Antes de hacer el ejercicio siguiente, asegúrese
de haber entendido las gráficas de la diapositiva
468.
622

623. 4. a) Recurriendo a la ecuación de provisión eficiente
entre un bien público y otro privado, encuentre estos
niveles de provisión cuando las funciones de utilidad
son
U1(x,y) = b1ln(x) + ln(y)
U2(x,y) = b2ln(x) + ln(y)
y la frontera de posibilidades de producción es
x + y = 100
b) Encuentre un mecanismo de provisión de estos
niveles.
5. Discuta la siguiente afirmación: “¿Por
qué es tan
común el impuesto a la gasolina? Porque se trata de un
impuesto Pigou para corregir tres externalidades negativas: Congestión, Accidentes y Polución.”
623

624. 5. a) Describir la “Paradoja de Condorcet” (siglo XVIII)
sobre las votaciones de mayoría simple.
b) Describir, de manera elemental, la inci-dencia de
las votaciones en la provisión de bienes públicos.
6. a)Describir, de manera sencilla, el “Teorema de
Imposibilidad de Arrow” de la elección social.
b) Describir, de manera elemental, la incidencia de
este teorema en la provisión de bienes públicos.
7. Discutir la “La tragedia de los bienes comunales”.
8. Leer los capítulos 32 y 35 del texto de Varian
intermedia (2007, Antoni Bosch).
624

625. CLASE
MAGISTRAL
#12
MERCADO BAJO INCERTIDUMBRE:
LA HIPÓTESIS DE LA UTILIDAD
ESPERADA
625

626. Hasta ahora, todas las decisiones tomadas por los
agentes se han hecho bajo certidumbre: un consumidor sabe, seguro, qué canasta va a consumir; un
productor sabe, seguro, qué cantidad de insumos va
a utilizar y qué cantidad de producto va a colocar en
el mercado, etc.
Ahora comenzaremos a estudiar estas mismas
elecciones pero bajo incertidumbre; es decir, las
acciones de los agentes no son acciones seguras
sino distribuciones sobre acciones.
626

627. Para comenzar, asumamos que usted tiene dos alternativas, L1 y L2, descritas así:
Bajo la alternativa L1, usted tira un dado. Si cae 1 ó 2
usted obtiene 200; pero si cae 3, 4, 5 ó 6, usted debe
pagar 100.
Por su parte, bajo la alternativa L2, usted escoge una
carta de póker. Si la carta es negra, usted paga
50; si es corazón rojo, obtiene un viaje a Cartagena
(con todo pagado) por 300; pero si es cualquier otra
carta roja, tendrá que pagar 100.
627

628. ¿Cuál alternativa escogerá usted? ¿Cómo valorar
cada una de estas?
Si existiera algún criterio que permitiera decidir si
L1> L2 , L2>L1 ó L1=L2 , en el sentido de cuál de las
dos alternativas ofrece mayores pagos, entonces
tendríamos posibilidad, inclusive de hacer teoría de
la elección, de la misma forma que lo hacíamos con la función de utilidad y las canastas
o con los planes de producción y los beneficios (o
el costo), en el caso de certidumbre.
628

629. Y, efectivamente, bajo ciertas condiciones, existe un criterio así y se llama el criterio de la utilidad
esperada. ¿Cómo opera? En el caso anterior de L1
y L2, tendremos lo siguiente:
Lotería L1
Resultado
Pago
Probabilidad
1
2
3
4
5
6
200
200
-100
-100
-100
-100
1/6
1/6
1/6
1/6
1/6
1/6
629

630. Lotería L2
Resultado
Carta negra
Corazón rojo
Otra carta roja
Pago
-50
300
-100
Probabilidad
26/52
13/52
13/52
i) En el caso de la lotería 1, la utilidad esperada es:
U1 = (1/6)(200) + (1/6)(200) + (1/6)(-100) + (1/6)(-100) + (1/6)(-100) + (1/6)(-100)
= 0
ii) Y en el caso de la lotería 2, la utilidad esperada es:
U2 = (26/52)(-50) + (13/52)(300) + (13/52)(-100)= (3900-2600)/52 = 25
De manera que, con este criterio, es preferible escoger la lotería 2 que la lotería
1.
630

631. Sin embargo, en la toma de decisiones con
incertidumbre es insuficiente el criterio de
valor monetario (dinero) esperado. Una
alternativa es el criterio de la utilidad
esperada. Precisamente de esta disyuntiva
surgió la famosa Paradoja de San Petersburgo
(Daniel Bernoulli, 1730), en donde se plantea:
“¿Es erróneo que se venda en 9,000 ducados un
billete de lotería que tiene iguales probabilidades
de obtener cero (0) ó 20,000 ducados?” (Notemos
que el valor monetario esperado de esta lotería
es 0.5(0) + 0.5(20,000) = 10,000 ducados).
Sin embargo, en este tipo de decisiones, aparecen
preferencias subjetivas ante el riesgo, que no
son tenidas en cuenta por el criterio del valor
monetario esperado
631

632. Otro ejemplo: Supongamos que un negocio A tiene tres
eventualidades, que son US$6000, US$4000 ó US$1000
de ganancia con probabilidades 0.3, 0.4 y 0.3 respectivamente. En este caso, el valor monetario esperado es
0.3(6,000) + 0.4(4,000) + 0.3(1,000)= US$3700. De otro
lado, en otro negocio B tiene las eventualidades de
perder US$10,000 ó de ganar US$20,000 ó US$7000
con probabilidades 0.5, 0.4 y 0.1, respectivamente.
También en este caso el valor monetario esperado es
0.5(-10,000) + 0.4(20,000) + 0.1(7,000)= US$3700.
632

633. Sin embargo, en la realidad algunos sujetos se inclinan
por una o por otra, más allá de que tengan el mismo
valor monetario esperado. Es así que se introducen
las preferencias subjetivas ante el riesgo por
parte de John von Neumann y Oskar Morgenstern
(1944): es la hipótesis de la utilidad esperada, que
mediante ciertas funciones de utilidad (llamadas
de von Neumann-Morgenstern), mide el valor
esperado, pero no en términos de ganancia, sino
de satisfacción, incluyendo allí las preferencias y
riesgos subjetivos ante situaciones inciertas.
633

634. La idea central es que la medida de ganancias y
pérdidas en moneda, en modo alguno es la misma
medida de utilidades y desutilidades económicas.
Así, una función de utilidad esperada von Neumann
Morgenstern (1944) es un índice numérico para
comparar situaciones inciertas en las que están
implicados criterios subjetivos importantes como la
disposición al riesgo.
634

635. Pero todo lo anterior lo debemos, en principio,
comenzar a adaptar para que pueda aplicarse bien a
la teoría del consumo y la producción:
i) En el caso de un consumidor con función de utilidad U, tomamos un conjunto de canastas, a1,
a2,…, an y le asignamos probabilidades respectivas
de ocurrencia p1, p2, …, pn, a cada una de ellas, de
tal forma que p1+p2+…+pn=1. Entonces, la utilidad esperada de esta lotería, en este caso, es:
E(U) = p1U(a1) + p2U(a2)+…+pn U(an)
635

636. ii) En el caso de un productor con función de
beneficios (o costos) π, tomamos un conjunto
de planes de producción (insumos-producción),
a1, a2,…, an y le asignamos probabilidades
respectivas de ocurrencia p1, p2, …, pn, a cada una
de ellas, de tal forma que p1+p2+…+pn=1.
Entonces, el beneficio esperado de esta lotería,
en este caso, es:
E(π) = p1π(a1) + p2π(a2)+…+pnπ (an)
636

637. Sin embargo, en general, el hecho de que una canasta
o plan de producción tenga una probabilidad de ser
consumida o llevado a cabo, respectivamente, depende
de circunstancias o eventos externos a los mismos
agentes económicos. Entonces la teoría ha dispuesto
de un nombre para ellos: se llaman “estados de la
naturaleza”. Por ejemplo, las épocas de lluvia o de sequía
son dos estados de la naturaleza que afectan de
manera distinta a los agentes económicos: a un consumidor el exceso de lluvias puede aumentarle su
consumo de bebidas calientes pero a un empresario
hotelero puede disminuirle sus ganancias, debido a la
posible baja ocupación.
637

638. Y así, dependiendo del estado de la naturaleza,
ahora sí, hacen sus planes de consumo y producción. A esto lo llaman un “plan contingente”. Es
decir, un plan contingente es una especificación de
las canastas a consumir o de los planes de producción a ejecutar, en cada estado de la naturaleza. A
este plan contingente también lo llaman una “lotería”. Es a estas loterías o planes contingentes
que se les toma el valor esperado tal como hicimos
antes, y luego podemos decidir cuál lotería es más
conveniente que otra. Demos un ejemplo de esto.
638

639. Dos planes contingentes (loterías) de
consumo y cinco estados de la naturaleza
S=1
S=2
C
2
3
C’
3
p(1)
Probabilidad
S=3
S=4
S=5
4
0
8
2
5
1
7
p(2)
p(3)
p(4)
p(5)
El plan contingente C paga E(U(C))= U(2)p(1)+ U(3)p(2)+ U(4)p(3) + U(0)p(4) + U(8)p(5)
El plan contingente C’ paga E(U(C’))= U(3)p(1)+ U(2)p(2)+ U(5)p(3)+ U(1)p(4) + U(7)p(5)
Para nuestro consumidor, el plan C es mejor que el plan C’ si E(U(C)) > E(U(C´))
639

640. Dos planes contingentes (loterías) de
producción y cinco estados de la naturaleza
S=1
S=2
S=3
S=4
S=5
C
( -1,2)
(-3,5)
(-4,7)
(0,0)
(-8,10)
C´
(-3,3)
(-2,1)
(-5,8)
(-1,1.5)
(-7,9)
p(2)
p(3)
p(4)
p(5)
Probabilidad p(1)
El plan contingente C paga E(π(C))= π(-1,2)p(1)+ π(-3,5)p(2)+ π(-4,7)p(3)
+ π(0,0)p(4) + π(-8,10)p(5)
El plan contingente C’ paga E(π(C’)) = π(-3,3)p(1)+ π(-2,1)p(2)+ π(-5,8)p(3)
+ π(-1,1.5)p(4) + π(-7,9)p(5)
Para nuestro consumidor, el plan C es mejor que el plan C’ si E(π(C))> E(π(C´))
640

641. Otro ejemplo
Suponga que un agricultor tiene una cantidad inicial
de trigo de 1000 Kg, y debe decidir qué cantidad
consumir y qué cantidad plantar para obtener más
trigo el año siguiente. Si llueve obtendrá 10 Kg de
trigo por cada Kg que planta. En cambio, si no llueve
obtendrá solo 5 Kg de trigo por cada Kg plantado.
La probabilidad de que llueva es ½. La función de
utilidad de este individuo es U(c0,c1) donde c0 y c1 son
los consumos en el primer y segundo periodo, respectivamente. El problema que se plantea el agricultor es cuánto trigo plantar.
641

642. Sea q la cantidad de Kgs. de trigo plantada en el
primer período. Entonces:
Consumo en el primer período= 1000 – q
10q
(si llueve)
Consumo en el segundo período
5q
(si no llueve)
Por lo tanto, el problema a resolver por parte del
agricultor es:
Maximizar (1/2)U(1000-q,10q) + (1/2)U(1000-q, 5q)
q≥0
642

643. A partir de todo lo anterior, es claro que para calcular el valor
esperado de un plan contingente de la forma C= (c(si)) (para n
estados de la naturaleza si con i=1,2,…, n), y con probabilidades
respectivas p(si), si vamos a utilizar la hipótesis del valor esperado,
debemos recurrir a la fórmula
E(U(C))= ∑i p(si) U(c(si))
Una función que mide de esta forma, lo dijimos antes, se llama función de utilidad von Neumann-Morgenstern (1944).
Y esto nos lleva a estudiar el comportamiento de la función de
utilidad U(c(si)) con respecto a eventos aleatorios. Advertimos,
de paso, que esto lo estudiaremos únicamente para una sola
variable (normalmente, dinero), entendiendo que es posible
extenderlo a varias variables.
643

644. U
pU(x) + (1-p)U(y )
U(px +(1-p)y)
Prefiere la utilidad
de la lotería
cierta px+(1-p)y,
a la utilidad esperada
p U(x) +(1-p)U(y)
de esa misma lotería
U(y)
•
•
Averso al riesgo
U(px+(1-p)y) > pU(x) +(1-p)U(y)
U(x)
x
px + (1-p)y
y
p=1
U
p=0
U
•
•
x
px+(1-p)y
Prefiere la utilidad
esperada
p U(x) +(1-p)U(y)
de la lotería, a
la utilidad
de la lotería
cierta px+(1-p)y
•
y
x
px+(1-p)y
Neutral al riesgo
Amante al riesgo
U(px+(1-p)y) = pU(x) +(1-p)U(y)
y
U(px+(1-p)y) < pU(x) +(1-p)U(y)
644

645. Medidas de aversión al riesgo
Como vimos en las gráficas anteriores, la concavidad
o convexidad de la función de utilidad nos dice
si un individuo es averso al riesgo o no. Entonces:
¿existe alguna forma de medir esa aversión y poder
decidir cuándo un individuo es más averso al riesgo
que otro? Es claro que si intentamos medir la concavidad, entonces la segunda derivada de la función
de utilidad estará involucrada.
645

646. Estudiaremos aquí, dos medidas de aversión al
riesgo desarrolladas por K. Arrow (1965) y J. Pratt
(1964):
1. La medida de aversión absoluta al riesgo de
Arrow-Pratt:
RA(w)= - U’’(w)/U’(w)
2. La medida de aversión relativa al riesgo de
Arrow- Pratt:
RR(w)= - w U’’(w)/U’(w)
646

647. Tres funciones de utilidad muy utilizadas en
la teoría del riesgo
1. Función Cuadrática:
U(w) = w - (b/2) w2
b>0
2. Función de aversión absoluta al riesgo (CARA):
U(w) = -(1/γ)e-γw
γ>0
3. Función de aversión relativa al riesgo constante
(CRRA):
U(w)= (w1-ς - 1)/(1-ς)
ς≥0
647

648. 1. Para la Función Cuadrática:
U(w)= w- (b/2) w2
se tiene que:
RA(w) = - U’’(w)/U’(w) = b/(1-bw)
b>0
,
w<(1/b)
RR(w) = - w U’’(w)/U’(w) = b w/(1-bw) , w<(1/b)
RA
1/b
w
Cuanto mayor
sea la renta,
mayor será la
aversión
(absoluta y
relativa) a
invertir en un
activo con
riesgo
RR
1/b
w
648

649. 1. Para la Función CARA:
U(w)= -(1/γ)e-γw
γ>0
se tiene que:
RA(w) = - U’’(w)/U’(w) = γ
,
RR(w) = - w U’’(w)/U’(w) = γw ,
RA
γ
w
Cuanto mayor
sea la renta,
mayor será la
aversión
relativa a
invertir en un
activo con
riesgo,
aunque la
aversión
absoluta es
constante
γ>0
γ>0
RR
RR = γw
w
649

650. Para la Función CRRA:
U(w)= ( w1-ς - 1)/(1-ς)
ς≥0
1. se tiene que:
RA(w) = - U’’(w)/U’(w) = ς/w ,
ς>0
RR(w) = - w U’’(w)/U’(w) = ς ,
ς>0
RA
RR = ς/w
w
Cuanto mayor
sea la renta,
menor será la
aversión
absoluta a
invertir en un
activo con
riesgo , y la
aversión
relativa a
invertir será
constante.
RR
RR = ς
w
650

651. Una ilustración simple
Retorno
medido por
utilidad
esperada
Acciones
Bonos corporativos
•
Bonos del Tesoro
•
•
averso
neutral
amante
Nivel de riesgo
Los principales factores de riesgo del mercado son la tasa de interés, la tasa
de cambio y el precio del activo.
651

652. Un caso particular importante
Se puede probar (lo harán en el Taller oficial
#3) que cuando ς tiende a 1, la
función de utilidad CRRA converge a la
función U(w)=ln(w). Por lo tanto, la
función de utilidad logarítmica es un caso
particular (límite) de la función CRRA, en el
que la aversión relativa al riesgo es 1.
652

653. 2. Una aplicación a la Información
Asimétrica
La información asimétrica en un mercado ocurre
cuando algún agente tiene información que los
otros agentes no tienen. Dos de los tipos de información asimétrica que más se estudian en la
literatura son los de “selección adversa” y “riesgo moral”.
653

654. 2. a) Los de selección adversa son, en general
(aunque no exclusivamente), modelos de
mercado, en el que uno de los agentes no
puede observar una característica inalterable
del bien que se comercia, y, así, el precio deja
de ser una señal de mercado perfecta del valor
de un bien, puesto que a un mismo precio se
pueden obtener bienes de diferente calidad;
además, puede dar origen a eliminación de
buenos productos, o incluso a la ausencia de
intercambio, en donde los equilibrios no son
óptimos de Pareto (second-best).
654

655. 2. b) Por su parte, los problemas de riesgo moral
son los que implican una acción o información
oculta. En general, se estructura a través de
modelos principal-agente, donde el principal es
el individuo que ordena al agente efectuar una
tarea estipulada en un contrato, pero que, a la
vez, enfrenta un problema de riesgo moral
cuando observa de manera imperfecta la acción
emprendida por el agente (acción oculta). El
problema del principal reside en encontrar un
incentivo para que el agente actúe de acuerdo
con su interés). Este es el origen de la teoría de
contratos.
655

656. Un ejemplo sencillo de selección adversa: el mercado
de carros usados
Consideremos un muy simple modelo de carros
usados en que todos los compradores son idénticos y
obtienen de su compra una utilidad U=C-P (diferencia
entre calidad y precio), y los vendedores una utilidad
V=P-C (diferencia entre precio y calidad). La mitad de
los automóviles es de buena calidad (C=20) y la otra
mitad es de mala calidad (C=10). Con información simétrica, los buenos carros serían comprados por 20 y
los de mala calidad por 10.
656

657. Con información asimétrica (es decir, los compradores
no conocen la calidad, sólo la información de que la
mitad es buena y la otra mitad es mala, además de los
niveles de C, en cada caso), la utilidad esperada de un
comprador al pagar un precio P es de
0.5(10-P) + 0.5(20-P) = 15-P
y a este nivel de utilidad, los compradores no pagarán
más de 10 por automóvil, y el vendedor, que sabe
esto, solo ofrecerá carros de mala calidad; es decir, los
carros de buena calidad son excluidos del mercado.
¡La selección adversa corresponde a un efecto perverso
que eliminó el producto de buena calidad!
657

658. Crítica a la Hipótesis de la Utilidad Esperada:
La Paradoja de Allais (Maurice Allais (1911-2010)
En 1953, Allais presenta una crítica a la Hipótesis de
la Utilidad Esperada (al principio ignorado, después
reconocido) que, parafraseada (Varian (1984)), es la siguiente:
$1’000,000
A
p=1
$1’000,000
C
$0
$5’000,000
$5’000,000
B
$1’000,000
D
$0
$0
¿En cada caso, cuál lotería preferiría usted?
p = 0.89
658

659. Muchos prefieren A a B y D a C. Pero veremos que
esto es contradictorio con un comportamiento estándar de la utilidad (esperada):
i) Una persona prefiere A a B (bajo utilidad esperada), si
U(1) > 0.1U(5) + 0.89U(1) + 0.01U(0)
Es decir, si
0.11U(1) > 0.1U(5) + 0.01U(0)
Y sumando 0.89U(0) a ambos lados, obtenemos que
0.11U(1) + 0.89U(0) > 0.1U(5) + 0.9U(0)
que significa que C es preferida a D.
659

660. Y…¿Qué sigue?
-Equilibrio general competitivo.
- Profundización en el estudio de las Fallas de
Mercado.
- Teoría de Juegos
- Síntesis neoclásica.
660

661. FINAL
Probablemente ocurra con la joven
microeconomía, lo que en otras disciplinas
maduras como la física o la biología: la
profundización de la incipiente fragmentación
actual, y la consagración de los métodos
experimentales.
661

662. Tareas para desarrollar con el profesor
asistente
1. Pruebe que cuando ς tiende a 1, la función de
utilidad CRRA converge a la función U(w)=ln(w). Por
lo tanto, la función de utilidad logarítmica es una
caso particular (límite) de la función CRRA, en el que
la aversión relativa al riesgo es 1.
2. Un consumidor puede elegir entre dos loterías: i) La
lotería L1 le proporciona 4000 unidades de renta con
probabilidad de 0.8, y 0 (cero) con probabilidad 0.2.
ii) La lotería L2 le proporciona 3000 unidades de renta
en todos los estados. Suponga que el individuo es
neutral al riesgo. ¿Cuál de las dos loterías elegiría? ¿Y
si fuera averso al riesgo con U(x)= ln(1000+x)?
662

663. 3. Un individuo que posee una riqueza W0, puede invertir
exclusivamente en dos activos financieros. Un activo
es seguro y, con independencia de la situación económica, le proporciona una rentabilidad del 20%. El
otro ofrece una rentabilidad del 50% si la economía
está en expansión y conlleva una pérdida del 50% en
situación recesiva. Con probabilidad π la economía se
encuentra en una fase expansiva. El individuo maximiza la utilidad esperada de la riqueza.
a) Si
X es la cantidad invertida en el activo con
riesgo, analice y represente la restricción
presupuestaria del individuo.
b) Si su función de utilidad de la riqueza cierta es
U(w)=ln(w), determine el valor de π de manera que el
individuo invierta la cuarta parte de su riqueza en el
activo seguro.
663

664. 4) Leer del texto de Varian intermedia
(2007, Antoni Bosch) los capítulos 12 y 36.
664