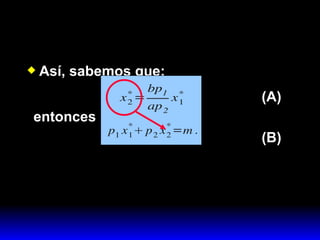
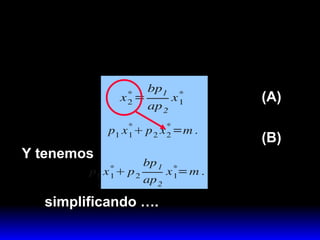
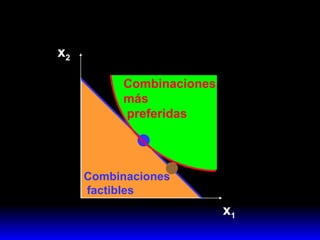
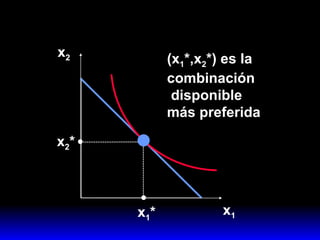
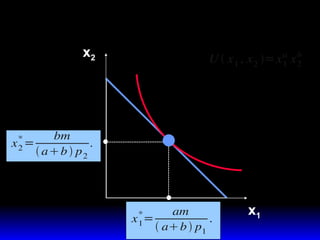
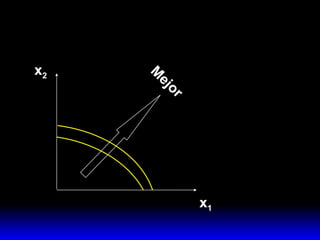
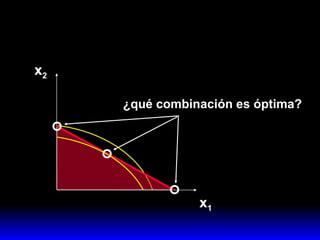
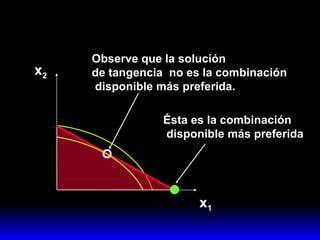
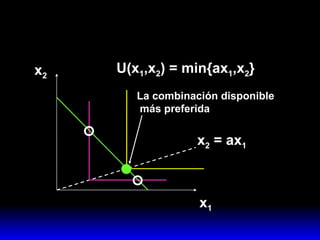
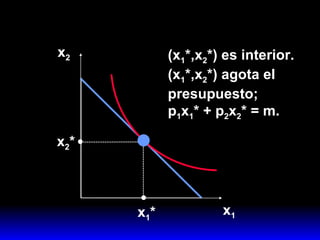
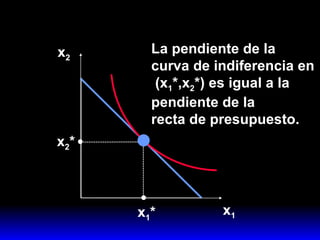
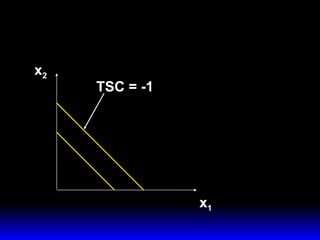
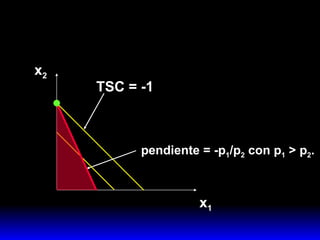
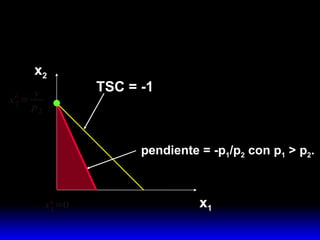
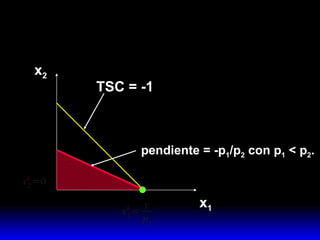
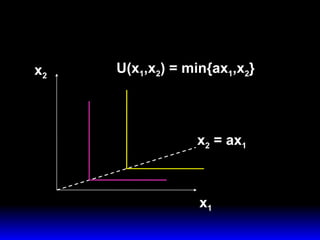
Este documento describe los conceptos fundamentales del óptimo del consumidor, incluyendo: 1) La combinación disponible más preferida por el consumidor que maximiza su satisfacción sujeta a su presupuesto. 2) Esta combinación óptima satisface dos condiciones: agota el presupuesto y iguala la pendiente de la curva de indiferencia a la pendiente de la recta de presupuesto. 3) La demanda ordinaria puede ser una solución interior o de esquina dependiendo de si el consumo de ambos bienes es positivo o si el consumo

1. Capítulo 5 Óptimo del Consumidor

2. Combinaciones factibles x 1 x 2 Combinaciones más preferidas

3. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es la combinación disponible más preferida

4. Cuando x 1 * > 0 y x 2 * > 0 la combinación demandada es INTERIOR . Si al comprar (x 1 *,x 2 *) el costo es $m entonces se agota el presupuesto.

5. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es interior. (x 1 *,x 2 *) agota el presupuesto; p 1 x 1 * + p 2 x 2 * = m.

6. x 1 x 2 x 1 * x 2 * La pendiente de la curva de indiferencia en (x 1 *,x 2 *) es igual a la pendiente de la recta de presupuesto.

7. (x 1 *,x 2 *) satisface dos condiciones: (a) agota el presupuesto: p 1 x 1 * + p 2 x 2 * = m (b) la pendiente de la recta de presupuesto, -p 1 /p 2 , y la pendiente de la curva de indiferencia que contiene a (x 1 *,x 2 *) son iguales en (x 1 *,x 2 *).

8. Estimando la demanda ordinario. Ejemplo Cobb-Douglas

9. Supongamos que las preferencias son del tipoCobb-Douglas

10. Y la TSC es:

11. La TSC es: En (x 1 *,x 2 *), TSC = -p 1 /p 2 entonces (A)‏

12. (x 1 *,x 2 *) agota el presupuesto, es decir: (B)‏

13. So now we know that (A)‏ (B)‏

14. Así, sabemos que: (A)‏ (B)‏ entonces

15. (A)‏ (B)‏ Y tenemos simplificando ….

17. Y siguiendo el mismo procedimiento

18. x 1 x 2

19. Pero ¿y si x 1 * = 0, o si x 2 * = 0?

20. Si x 1 * = 0 ó x 2 * = 0 entonces la demanda ordinaria (x 1 *,x 2 *) es una solución de esquina .

21. x 1 x 2 TSC = -1

22. x 1 x 2 TSC = -1 pendiente = -p 1 /p 2 con p 1 > p 2 .

23. x 1 x 2 TSC = -1 pendiente = -p 1 /p 2 con p 1 > p 2 .

24. x 1 x 2 TSC = -1 pendiente = -p 1 /p 2 con p 1 < p 2 .

25. Ejemplos de soluciones de esquina: el caso de preferencias no convexas

26. x 1 x 2 Mejor

27. x 1 x 2 ¿qué combinación es óptima?

28. x 1 x 2 Ésta es la combinación disponible más preferida Observe que la solución de tangencia no es la combinación disponible más preferida.

29. Ejemplos de soluciones en vértice. El caso de bienes complementarios perfectos

30. x 1 x 2 U(x 1 ,x 2 ) = min{ax 1 ,x 2 } x 2 = ax 1

31. x 1 x 2 U(x 1 ,x 2 ) = min{ax 1 ,x 2 } x 2 = ax 1 La combinación disponible más preferida

32. x 1 x 2 U(x 1 ,x 2 ) = min{ax 1 ,x 2 } x 2 = ax 1 x 1 * x 2 * (a) p 1 x 1 * + p 2 x 2 * = m (b) x 2 * = ax 1 *

33. (a) p 1 x 1 * + p 2 x 2 * = m; (b) x 2 * = ax 1 *. Substituyendo (b) en (a) llegamos a

34. El costo de una combinación de 1 unidad del bien 1 y a unidades del bien 2 es p 1 + a p 2 ; m/(p 1 + a p 2 ) es el máximo número de estas combinaciones.