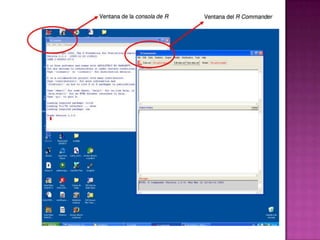
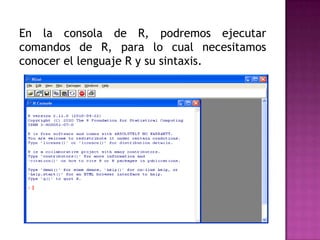
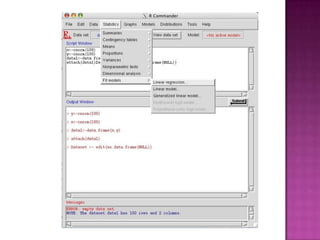
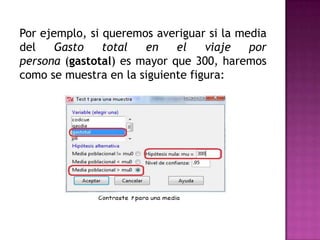
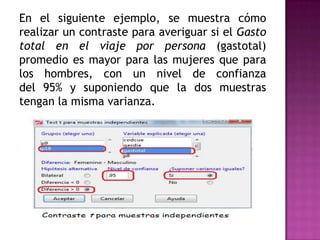
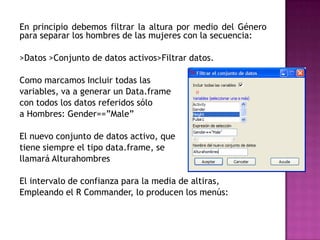
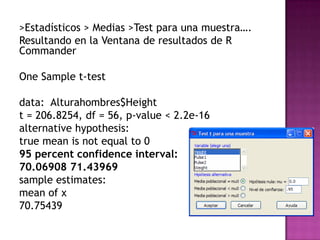
El documento explica la definición de hipótesis y pruebas de hipótesis en estadística, destacando su uso para verificar aseveraciones sobre poblaciones mediante datos muestrales. Se presenta R Commander, una interfaz gráfica que facilita el uso del entorno estadístico R sin necesidad de conocer su lenguaje de comandos. Además, se ejemplifican contrastes de hipótesis, incluidos test t para medias y proporciones, utilizando conjuntos de datos específicos.

1. DOCENTE: Dra. Silvia Haro.
NOMBRE: Daniela Rocío Carrasco Cayambe.

3. Para el desarrollo de nuestro mini manual
empezaremos definiendo que es una hipótesis y
que es una prueba de hipótesis:

Hipótesis es una aseveración de una población
elaborado con el propósito de poner a prueba,
para verificar si la afirmación es razonable, se
usan datos. En el análisis estadístico se hace una
aseveración, es decir, se plantea una hipótesis,
después se hacen las pruebas para verificar la
aseveración o para determinar que no es
verdadera.

Por tanto, diremos que la Prueba de hipótesis es
un procedimiento basado en la evidencia
muestral y la teoría de probabilidad; se emplea
para determinar si la hipótesis es una afirmación
razonable.

4. Se trata de un proyecto de software libre.
R-Commander se denomina como una Interfaz
Gráfica de Usuario (GUI en inglés), creada por
John Fox, que permite acceder a muchas
capacidades del entorno estadístico R sin que el
usuario tenga que conocer el lenguaje de
comandos propio de este entorno. Al iniciar RCommander, se nos presentan dos ventanas:

6. En la consola de R, podremos ejecutar
comandos de R, para lo cual necesitamos
conocer el lenguaje R y su sintaxis.

7. El entorno de R-commander, nos evita precisamente
tener que usar dicho lenguaje de comandos, al menos
para las tareas que se encuentran implementadas
dentro de dicho entorno.
No obstante, R-Commander no pretende ocultar el
lenguaje R. Si observamos de cerca la ventana de RCommander, vemos que se divide en tres subventanas:
script, output y messages. Cada vez que, a través de los
menús de R-commander accedamos a las capacidades
de
R
(gráficos,
procedimientos
estadísticos, modelos, etc.), en la ventana script se
mostrará el comando R que ejecuta la tarea que
hayamos solicitado, y en la ventana output se mostrará
el resultado de dicho comando. De este modo, aunque
el usuario no conozca el lenguaje de comandos de
R, simplemente observando lo que va apareciendo en la
ventana script se irá familiarizando con dicho lenguaje.

10. Test t para una muestra Sirve para hacer
contrastes de hipótesis para la media de una
variable cuantitativa con distribución normal.
En la pantalla de construcción del contraste se
pueden elegir:
tipo
de
contraste
—
bilateral
(igualdad), unilaterales (menor o mayor);
valor de la media bajo la hipótesis nula;
nivel de confianza para el intervalo de
estimación.

11. Por ejemplo, si queremos averiguar si la media
del
Gasto
total
en
el
viaje
por
persona (gastotal) es mayor que 300, haremos
como se muestra en la siguiente figura:

12. Mostraremos su salida:

13. Realiza un contraste de hipótesis de igualdad
de medias entre dos muestras. Se necesita por
un lado una variable cuantitativa y, por
otro, una variable dicotómica (cualitativa o
factor, con sólo dos modalidades) que indique
los dos grupos (por ejemplo, el sexo).

14. En el siguiente ejemplo, se muestra cómo
realizar un contraste para averiguar si el Gasto
total en el viaje por persona (gastotal)
promedio es mayor para las mujeres que para
los hombres, con un nivel de confianza
del 95% y suponiendo que la dos muestras
tengan la misma varianza.

15. Mostraremos su salida:

16. Contraste la hipótesis nula de que la
proporción de respuesta positiva después del
parto (aclact1) es igual a 0,5. Construya el
intervalo de confianza al 95% para la
proporción poblacional de respuesta positiva.

18. Resultados
Deberemos rechazar la hipótesis nula de que la proporción sea 0,5 con
p=0,002304.
Nótese que el estadístico X-squared (ji-cuadrado) es equivalente en
valor de p a la prueba z para una proporción.

20.  Con
el conjunto de datos de Pulsos,
queremos estudiar la altura media de los
hombres solamente, por medio de un
intervalo de confianza al nivel de
significación =0.05, o de confianza del 95%, y
utilizarlo para contrastar la hipótesis de si la
altura media de los hombres es de 171 cms.
Vamos a generar un conjunto de datos con
las alturas de los hombres.

21. En principio debemos filtrar la altura por medio del Género
para separar los hombres de las mujeres con la secuencia:
>Datos >Conjunto de datos activos>Filtrar datos.
Como marcamos Incluir todas las
variables, va a generar un Data.frame
con todos los datos referidos sólo
a Hombres: Gender==”Male”
El nuevo conjunto de datos activo, que
tiene siempre el tipo data.frame, se
llamará Alturahombres
El intervalo de confianza para la media de altiras,
Empleando el R Commander, lo producen los menús:

22. >Estadísticos > Medias >Test para una muestra….
Resultando en la Ventana de resultados de R
Commander
One Sample t-test
data: Alturahombres$Height
t = 206.8254, df = 56, p-value < 2.2e-16
alternative hypothesis:
true mean is not equal to 0
95 percent confidence interval:
70.06908 71.43969
sample estimates:
mean of x
70.75439

23. Basándonos en el intervalo de confianza para
la media de alturas de hombres: (70.06908
71.43969) consideremos ahora el contraste de
hipótesis sobre que la altura media es 171 cms.
Pasando esta altura media a pulgadas, que es
la información extraída de la tabla: 171/2.54=
67.3228 pulgadas.
Se concluye afirmando con el 95% de
confianza que la altura media no es 171
cms, pues 67.3228 pulgadas no está
contenido en el intervalo de confianza
calculado.

24. FIN