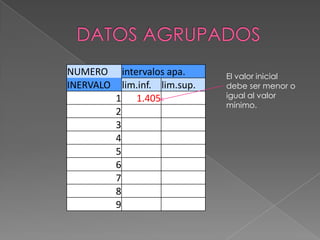
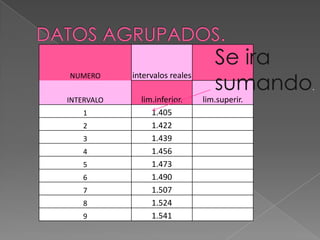
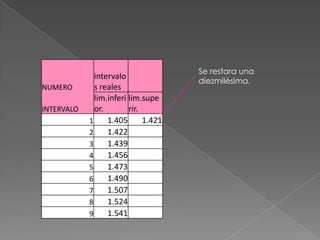
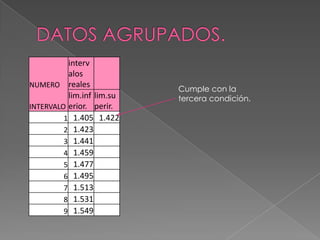
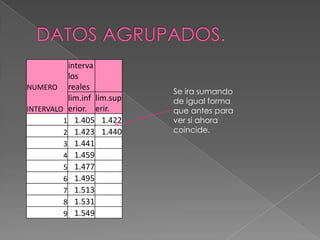
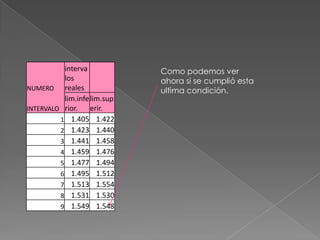
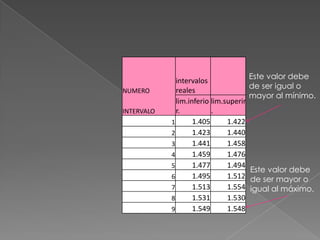
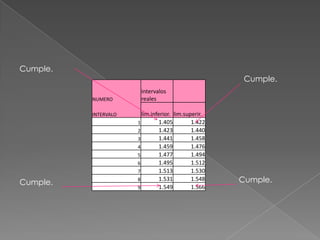
Este documento describe los pasos para calcular intervalos aparentes a partir de un conjunto de datos. Primero se encuentran los valores máximo y mínimo para calcular el rango de los datos. Luego se determina el número de intervalos y el tamaño de cada intervalo dividiendo el rango entre la cantidad de intervalos. Finalmente, se construyen los intervalos aparentes asignando valores a los límites inferior y superior de cada uno.

2.  En el desarrollo de esta presentación se
mostrara e identificara cada uno de los
pasos de cómo poder averiguar lo que
es llamado intervalos aparentes.
 Se mostrara todas las operaciones para
este trabajo de forma clara y detenida
para un mejor entendimiento.

3.  PROCEDIMIENTO.
Se realizara el siguiente ejemplo de
acuerdo a las siguientes
especificaciones.
Se agruparan en 9 intervalos.

4. 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 1,444 1,488 1,51 1,489 1,566 1,545 1,534 1,423 1,488 1,532 1,49 1,544 1,457 1,475 1,563
2 1,413 1,424 1,469 1,524 1,499 1,512 1,487 1,551 1,481 1,502 1,496 1,443 1,463 1,46 1,484
3 1,484 1,547 1,554 1,394 1,471 1,492 1,476 1,508 1,543 1,497 1,486 1,493 1,538 1,518 1,5
6 1,555 1,49 1,456 1,539 1,522 1,576 1,498 1,529 1,494 1,526 1,469 1,488 1,478 1,495 1,521
4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 1.464 1.507 1.582 1.588 1.455 1.447 1.439 1.479 1.506 1.514 1.482 1.519 1.465 1.479 1.508
5 1,467 1,558 1,511 1,515 1,561 1,445 1,515 1,526 1,491 1,523 1,521 1,559 1,482 1,441 1,529
2 1.528 1.514 1.484 1.522 1.500 1.459 1.488 1.540 1.525 1.494 1.536 1.458 1.475 1.487 1.483
3 1.454 1.507 1.445 1.500 1.466 1.452 1.468 1.465 1.505 1.490 1.491 1.512 1.516 1.513 1.505
6 1,516 1,531 1,435 1,48 1,513 1,535 1,469 1,503 1,453 1,535 1,53 1,512 1,499 1,467 1,508
1.463 1.525 1.519 1.497 1.513 1.476 1.494 1.494 1.481 1.505 1.488 1.531 1.456 1.456 1.522
7 1,482 1,577 1,487 1,437 1,44 1,533 1,54 1,481 1,49 1,499 1,496 1,526 1,505 1,512 1,544
6 1.525 1.546 1.497 1.536 1.464 1.492 1.492 1.518 1.444 1.537 1.531 1.494 1.498 1.509 1.509
7 1.562 1.543 1.503 1.545 1.532 1.471 1.468 1.495 1.520 1.467 1.494 1.497 1.515 1.529 1.492
8 1,519 1,484 1,562 1,506 1,529 1,424 1,545 1,45 1,539 1,548 1,51 1,474 1,469 1,469 1,54
8 1.524 1.485 1.513 1.487 1.447 1.451 1.440 1.487 1.532 1.518 1.517 1.505 1.536 1.478 1.525
9 1.461 1.485 1.489 1.423 1.487 1.517 1.491 1.453 1.477 1.499 1.513 1.459 1.528 1.483 1.493
9 1,533 1,545 1,546 1,506 1,487 1,511 1,554 1,494 1,472 1,46 1,479 1,483 1,467 1,528 1,492
10 1.479 1.498 1.536 1.477 1.491 1.504 1.457 1.480 1.518 1.466 1.480 1.469 1.522 1.489 1.542
10 1,53 1,531 1,528 1,449 1,505 1,528 1,466 1,537 1,424 1,518 1,494 1,463 1,554 1,488 1,537

5. 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
1,506 1,571 1,49 1,54 1,507 1,483 1,519 1,528 1,551 1,509 1,434 1,484 1,481 1,498 1,469
1.480 1.490 1.503 1.444 1.502 1.510 1.514 1.482 1.512 1.544 1.450 1.449 1.467 1.550 1.519
1,553 1,494 1,549 1,512 1,481 1,482 1,441 1,515 1,454 1,49 1,474 1,45 1,508 1,454 1,515
1.483 1.512 1.400 1.483 1.501 1.502 1.484 1.481 1.485 1.509 1.462 1.466 1.448 1.527 1.470
1,537 1,496 1,431 1,489 1,532 1,447 1,479 1,503 1,51 1,547 1,458 1,489 1,455 1,411 1,465
1.486 1.449 1.549 1.544 1.492 1.578 1.499 1.489 1.474 1.461 1.530 1.520 1.479 1.541 1.511
1,432 1,473 1,474 1,458 1,448 1,461 1,521 1,49 1,489 1,479 1,484 1,461 1,496 1,491 1,455
1.503 1.539 1.500 1.477 1.515 1.481 1.510 1.526 1.484 1.455 1.494 1.518 1.581 1.488 1.480
1,498 1,467 1,492 1,501 1,468 1,441 1,504 1,569 1,462 1,46 1,502 1,512 1,524 1,473 1,44
1.510 1.500 1.479 1.516 1.506 1.558 1.506 1.523 1.447 1.484 1.514 1.535 1.488 1.546 1.463
1.494 1.484 1.493 1.443 1.536 1.514 1.505 1.498 1.491 1.512 1.481 1.464 1.462 1.493 1.485
1,492 1,49 1,549 1,506 1,479 1,491 1,55 1,501 1,52 1,485 1,459 1,462 1,488 1,501 1,476
1.503 1.497 1.502 1.502 1.521 1.496 1.552 1.532 1.502 1.500 1.562 1.436 1.455 1.494 1.517
1,492 1,483 1,474 1,494 1,515 1,507 1,527 1,551 1,541 1,467 1,48 1,514 1,516 1,508 1,471
1.499 1.527 1.497 1.483 1.472 1.466 1.516 1.526 1.503 1.455 1.534 1.463 1.449 1.467 1.440
1,484 1,504 1,489 1,512 1,564 1,456 1,424 1,482 1,492 1,553 1,485 1,495 1,538 1,515 1,471
1.574 1.534 1.590 1.495 1.528 1.552 1.546 1.472 1.472 1.511 1.552 1.490 1.480 1.500 1.548
1,484 1,528 1,547 1,503 1,501 1,491 1,531 1,578 1,469 1,458 1,496 1,483 1,531 1,492 1,51
1.502 1.481 1.515 1.511 1.513 1.491 1.527 1.495 1.431 1.486 1.494 1.517 1.567 1.528 1.535
1,449 1,491 1,557 1,481 1,483 1,405 1,483 1,46 1,443 1,467 1,491 1,502 1,468 1,499 1,501

6.  PRIMERO.
Se encontraran los valores máximo y
mínimo del ejercicio para poder calcular el
rango.
máximo.= 1.566
mínimo.=1.405
rango.=0.161.
Tamaño del intervalo.=0.017

7.  SEGUNDO.
Determinar el numero de intervalos se
puede determinar por medio de una raíz
cuadrada pero en este caso como
tenemos las especificaciones
(arbitrariamente) serán 9 intervalos.

8.  TERCERO.
Se determinara el tamaño de los intervalos.
Para esto se divide lo que es el resultado del
rango sobre el numero de intervalos.
0.161/9 = 0.017
En este caso como los números son muy
pequeños se recomienda aumentar una
diezmilésima al tamaño del intervalo.

9.  CUARTO.
construiremos enseguida los 9 intervalos
aparentes.
Para esto hay muchas formas pero
seguiremos la siguiente.
Se escoge un numero que sea igual o mayor
al valor mínimo se recomienda usar el valor
mínimo como inicio para una mejor
precisión.
Valor mínimo=1.405.

10. NUMERO intervalos apa. El valor inicial
INERVALO lim.inf. lim.sup. debe ser menor o
1 1.405 igual al valor
mínimo.
2
3
4
5
6
7
8
9

11.  apartar de este valor se crearan los
limites inferiores lo que se tendrá que
hacer será ir sumando el valor del
tamaño del intervalo las veces que se
requiera.
 Pero antes de darle seguimiento al
proceso debemos de comprobar de
que cumpla con lo requerido.
 Como vemos enseguida si se cumplió.

12. Se ira
sumando
NUMERO intervalos reales
.
INTERVALO lim.inferior. lim.superir.
1 1.405
2 1.422
3 1.439
4 1.456
5 1.473
6 1.490
7 1.507
8 1.524
9 1.541

13. interv
alos En este caso se
NUMERO reales cumplió con las
lim.inf lim.su condiciones.
INTERVALO erior. perir.
1 1.405
2 1.422
3 1.439
4 1.456
5 1.473
6 1.490
7 1.507
8 1.524
9 1.541

14.  Ahora proseguiremos con sacar el
primer limite superior.
 En este caso se tendrá que restar una
diezmilésima al segundo valor del limite
inferior.
 Segundo lim. Inferior=1.421
 Menos una diezmilésima=1420
 El primer limite superior será=1420

15. Se restara una
intervalo
diezmilésima.
NUMERO s reales
lim.inferi lim.supe
INTERVALO or. rir.
1 1.405 1.421
2 1.422
3 1.439
4 1.456
5 1.473
6 1.490
7 1.507
8 1.524
9 1.541

16.  Ahora se volverá hacer el mismo
procedimiento que se uso con los limites
inferiores.
 Que será ir sumando el valor del tamaño
del intervalo.

17. interva
los Debe ser igual o
NUMERO reales mayor al valor
lim.inf lim.su mínimo.
INTERVALO erior. perir.
1 1.405 1.421
2 1.422 1.438
Debe de ser igual o
3 1.439 1.455 mayor que el valor
4 1.456 1.472 maximo
5 1.473 1.489
6 1.490 1.506
7 1.507 1.523
8 1.524 1.540
9 1.541 1.557

18. Ahora tendremos que revisar que los limites
cumplan con lo especificado.
Vemos que no se pudo cumplir lo deseado lo
que hace que volvamos a realizarlo otra
vez.
Vemos que solo tres condiciones se llegan a
cumplir pero la ultima no lo logro por lo que
proseguiremos.
Y averiguar cual fue el error.

19. Tendremos que revisar el tamaño del intervalo
para ver si es el adecuado para el problema si
no lo es tendremos que aumentarle una
diezmilésima al valor de este para que se
adecue y pueda cumplir con las condiciones
necesarias.
Si no hubiera sido el caso del problema
tendríamos que cambiar el numero de
intervalos.
Enseguida veremos como queda de forma
adecuada.
Cumpliendo con todas las condiciones.

20. intervalo Cumple con la
NUMERO s reales primera
lim.inferi lim.supe condición
INTERVALO or. rir.
1 1.405
2
3
4
5
6
7
8
9

21. interval
os
NUMERO reales
Cumple con la
lim.infe lim.sup segunda condición.
INTERVALO rior. erir.
1 1.405
2 1.423
3 1.441
4 1.459
5 1.477
6 1.495
7 1.513
8 1.531
9 1.549

22. interv
alos
NUMERO reales
Cumple con la
lim.inf lim.su tercera condición.
INTERVALO erior. perir.
1 1.405 1.422
2 1.423
3 1.441
4 1.459
5 1.477
6 1.495
7 1.513
8 1.531
9 1.549

23. interva
los
NUMERO reales
Se ira sumando
lim.inf lim.sup de igual forma
INTERVALO erior. erir. que antes para
1 1.405 1.422 ver si ahora
2 1.423 1.440 coincide.
3 1.441
4 1.459
5 1.477
6 1.495
7 1.513
8 1.531
9 1.549

24. interva Como podemos ver
los ahora si se cumplió esta
NUMERO reales ultima condición.
lim.infe lim.sup
INTERVALO rior. erir.
1 1.405 1.422
2 1.423 1.440
3 1.441 1.458
4 1.459 1.476
5 1.477 1.494
6 1.495 1.512
7 1.513 1.554
8 1.531 1.530
9 1.549 1.548

25. intervalos Este valor debe
intervalos
NUMERO reales de ser igual o
NUMERO reales
lim.inferi lim.superi mayor al mínimo.
lim.inferio lim.superir
INTERVALO or. r.
INTERVALO r. .
1 1.400 1.421
1 1.405 1.422
2 1.422
1.423 1.443 1.440
2
3
3 1.444
1.441 1.465 1.458
4
4 1.466
1.459 1.487 1.476
5
5 1.487
1.477 1.509 1.494
Este valor debe
6
6 1.510
1.495 1.532 1.512 de ser mayor o
7
7 1.532
1.513 1.554 1.554 igual al máximo.
8
8 1.553
1.531 1.576 1.530
9
9 1.575
1.549 1.597 1.548

26. Cumple.
Cumple.
intervalos
NUMERO reales
INTERVALO lim.inferior. lim.superir.
1 1.405 1.422
2 1.423 1.440
3 1.441 1.458
4 1.459 1.476
5 1.477 1.494
6 1.495 1.512
7 1.513 1.530
Cumple. 8 1.531 1.548 Cumple.
9 1.549 1.566

27.  Como pudimos observar el la tabla anterior
se cumplieron todos los requisitos
necesarios los cuales se usan cuando el
problema será resuelto a mano.
 Aunque lo que hicimos es en realidad para
poder encontrar los intervalos reales.
 Los cuales explicaremos en la siguiente
presentación.