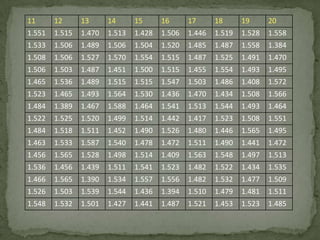
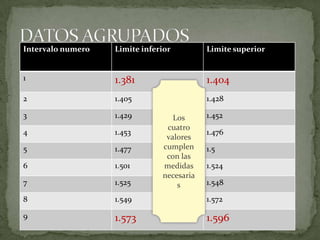
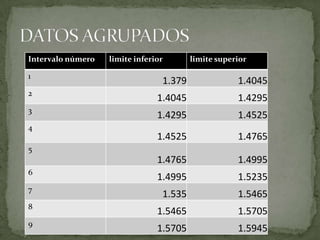
Este documento presenta los pasos para agrupar datos en intervalos, incluyendo calcular las medidas de tendencia central y dispersión para los datos agrupados. Muestra un ejemplo de cómo completar una tabla agrupando datos en 9 intervalos reales, dividiendo la distancia entre cada par de intervalos entre dos para obtener los límites inferiores y superiores precisos. El objetivo es mostrar las operaciones necesarias para reducir datos agrupándolos en intervalos.

1. Alfredo Rosales Vázquez

2.  En esta presentación el objetivo es mostrar las
operaciones aritméticas necesarias para reducir datos
agrupándolos en intervalos.
 Se presenta el calculo de intervalos reales de las
medidas de tendencia central y dispersión ms usadas.

3.  Procedimiento para datos agrupados
 Ejemplo: completar la tabla que se muestra a
continuación agrupándolos en 9 intervalos.

4. 10 1 2 3 4 5 6 7 8 9 10
1 1.457 1.408 1.502 1.501 1.382 1.535 1.518 1.503 1.500 1.565
2 1.461 1.585 1.454 1.502 1.569 1.446 1.455 1.484 1.421 1.514
3 1.477 1.463 1.512 1.479 1.488 1.497 1.452 1.492 1.499 1.504
4 1.533 1.494 1.535 1.529 1.514 1.484 1.511 1.485 1.511 1.522
5 1.503 1.565 1.440 1.558 1.542 1.481 1.422 1.481 1.530 1.458
6 1.512 1.515 1.490 1.594 1.519 1.509 1.486 1.495 1.519 1.528
7 1.527 1.467 1.494 1.515 1.510 1.432 1.501 1.463 1.491 1.489
8 1.481 1.530 1.482 1.502 1.489 1.507 1.547 1.586 1.427 1.454
9 1.496 1.524 1.486 1.404 1.516 1.491 1.500 1.497 1.519 1.502
10 1.540 1.541 1.503 1.561 1.461 1.536 1.536 1.552 1.516 1.529
11 1.469 1.455 1.540 1.478 1.513 1.510 1.559 1.516 1.472 1.527
12 1.493 1.523 1.500 1.547 1.553 1.474 1.440 1.525 1.472 1.545
13 1.475 1.503 1.536 1.505 1.449 1.506 1.541 1.504 1.502 1.558
14 1.521 1.471 1.465 1.441 1.404 1.485 1.552 1.423 1.494 1.471
15 1.452 1.501 1.430 1.464 1.529 1.517 1.472 1.521 1.453 1.495

5. 11 12 13 14 15 16 17 18 19 20
1.551 1.515 1.470 1.513 1.428 1.506 1.446 1.519 1.528 1.558
1.533 1.506 1.489 1.506 1.504 1.520 1.485 1.487 1.558 1.384
1.508 1.506 1.527 1.570 1.554 1.515 1.487 1.525 1.491 1.470
1.506 1.503 1.487 1.451 1.500 1.515 1.455 1.554 1.493 1.495
1.465 1.536 1.489 1.515 1.515 1.547 1.503 1.486 1.408 1.572
1.523 1.465 1.493 1.564 1.530 1.436 1.470 1.434 1.508 1.566
1.484 1.389 1.467 1.588 1.464 1.541 1.513 1.544 1.493 1.464
1.522 1.525 1.520 1.499 1.514 1.442 1.417 1.523 1.508 1.551
1.484 1.518 1.511 1.452 1.490 1.526 1.480 1.446 1.565 1.495
1.463 1.533 1.587 1.540 1.478 1.472 1.511 1.490 1.441 1.472
1.456 1.565 1.528 1.498 1.514 1.409 1.563 1.548 1.497 1.513
1.536 1.456 1.439 1.511 1.541 1.523 1.482 1.522 1.434 1.535
1.466 1.565 1.390 1.534 1.557 1.556 1.482 1.532 1.477 1.509
1.526 1.503 1.539 1.544 1.436 1.394 1.510 1.479 1.481 1.511
1.548 1.532 1.501 1.427 1.441 1.487 1.521 1.453 1.523 1.485

6.  A continuación se llevara acabo los primeros cuatro
pasos para obtener los intervalos aparentes.

7. Intervalo numero Limite inferior Limite superior
1 1.381 1.404
2 1.405 1.428
3 1.429 Los 1.452
cuatro
4 1.453 1.476
valores
5 1.477 cumplen 1.5
con las
6 1.501 medidas 1.524
necesaria
7 1.525 s 1.548
8 1.549 1.572
9 1.573 1.596

8.  Quinto paso:
 Obtener intervalos reales
 Para obtener estos necesitamos calcular la
distancia de un intervalo a otro.
 Primer intervalo tomar cualquier par de intervalos
de1.381 a 1.404
 segundo intervalo de 1.405 a 1.428

9.  Quinto paso:
 Primer intervalo de1.381 a 1.404
 Segundo intervalo de 1.405 a 1.428
 La distancia entre estos intervalos es la diferencia entre
el limite inferior del segundo intervalo(1.405 )y el
limite superior del primero(1.404)
 Ahora restamos 1.405 - 1.404=0.001

10.  Quinto paso obtener intervalos reales restando 1.405 -
1.404=0.001
 Dividimos esta distancia entre dos:
 0.001 / 2= 0.0005
 Este resultado obtenido se le restara a los limites
inferiores, y a los limites superiores se les sumara.

11. Intervalo numero Limite inferior Limite superior
1 1.381- 0.0005 1.404 + 0.0005
2 1.405 - 0.0005 1.428 + 0.0005
3 1.429 -0.0005 1.452 + 0.0005
4 1.453 -0.0005 1.476 + 0.0005
5 1.477 -0.0005 1.5 + 0.0005
6 1.501 -0.0005 1.524+ 0.0005
7 1.525 -0.0005 1.548 + 0.0005
8 1.549 -0.0005 1.572 + 0.0005
9 1.573 -0.0005 1.596 + 0.0005

12. Intervalo número limite inferior limite superior
1
1.379 1.4045
2
1.4045 1.4295
3
1.4295 1.4525
4
1.4525 1.4765
5
1.4765 1.4995
6
1.4995 1.5235
7
1.535 1.5465
8
1.5465 1.5705
9
1.5705 1.5945

13.  Quinto paso.
 Ya que tenemos los intervalos reales se pondrán en una
tabla que se les mostrara despues.

14. Teo_billy_3p@hotmail.com
Probanilidad1.bligoo.com
Gracias por su atención