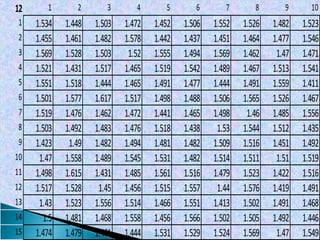
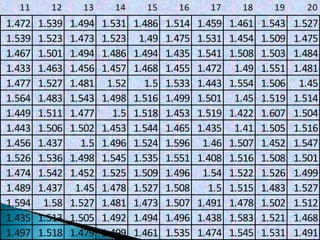
Este documento explica paso a paso cómo calcular intervalos aparentes para un conjunto de 300 datos. Primero se encuentran el valor máximo (1.617), mínimo (1.408) y rango (0.209). Luego se divide el rango entre 12 intervalos para obtener un tamaño de intervalo de 0.017. Finalmente, se generan los 12 intervalos aparentes sumando sucesivamente el tamaño de intervalo al valor inferior.

2.  En esta presentación les explicare como paso a paso, para que
realices los intervalos aparentes
 El objetivo de la presentación es mostrar detalladamente las
operaciones para así lograr terminar los intervalos aparentes.

3.  El ejemplo es el siguiente, son 300 datos que representan las
medidas de unos pernos.
 A continuación muestro la tabla.

4. 12 1 2 3 4 5 6 7 8 9 10
1 1.534 1.448 1.503 1.472 1.452 1.506 1.552 1.526 1.482 1.523
2 1.455 1.461 1.482 1.578 1.442 1.437 1.451 1.464 1.477 1.546
3 1.569 1.528 1.503 1.52 1.555 1.494 1.569 1.462 1.47 1.471
4 1.521 1.431 1.517 1.465 1.519 1.542 1.489 1.467 1.513 1.541
5 1.551 1.518 1.444 1.465 1.491 1.477 1.444 1.491 1.559 1.411
6 1.501 1.577 1.617 1.517 1.498 1.488 1.506 1.565 1.526 1.467
7 1.519 1.476 1.462 1.472 1.441 1.465 1.498 1.46 1.485 1.556
8 1.503 1.492 1.483 1.476 1.518 1.438 1.53 1.544 1.512 1.435
9 1.423 1.49 1.482 1.494 1.481 1.482 1.509 1.516 1.451 1.492
10 1.47 1.558 1.489 1.545 1.531 1.482 1.514 1.511 1.51 1.519
11 1.498 1.615 1.431 1.485 1.561 1.516 1.479 1.523 1.422 1.516
12 1.517 1.528 1.45 1.456 1.515 1.557 1.44 1.576 1.419 1.491
13 1.43 1.523 1.556 1.514 1.466 1.551 1.413 1.502 1.491 1.468
14 1.5 1.481 1.468 1.558 1.456 1.566 1.502 1.505 1.492 1.446
15 1.474 1.479 1.461 1.444 1.531 1.529 1.524 1.569 1.47 1.549

5. 11 12 13 14 15 16 17 18 19 20
1.472 1.539 1.494 1.531 1.486 1.514 1.459 1.461 1.543 1.527
1.539 1.523 1.473 1.523 1.49 1.475 1.531 1.454 1.509 1.475
1.467 1.501 1.494 1.486 1.494 1.435 1.541 1.508 1.503 1.484
1.433 1.463 1.456 1.457 1.468 1.455 1.472 1.49 1.551 1.481
1.477 1.527 1.481 1.52 1.5 1.533 1.443 1.554 1.506 1.45
1.564 1.483 1.543 1.498 1.516 1.499 1.501 1.45 1.519 1.514
1.449 1.511 1.477 1.5 1.518 1.453 1.519 1.422 1.607 1.504
1.443 1.506 1.502 1.453 1.544 1.465 1.435 1.41 1.505 1.516
1.456 1.437 1.5 1.496 1.524 1.596 1.46 1.507 1.452 1.547
1.526 1.536 1.498 1.545 1.535 1.551 1.408 1.516 1.508 1.501
1.474 1.542 1.452 1.525 1.509 1.496 1.54 1.522 1.526 1.499
1.489 1.437 1.45 1.478 1.527 1.508 1.5 1.515 1.483 1.527
1.594 1.58 1.527 1.481 1.473 1.507 1.491 1.478 1.502 1.512
1.435 1.513 1.505 1.492 1.494 1.496 1.438 1.583 1.521 1.468
1.497 1.518 1.479 1.499 1.461 1.535 1.474 1.545 1.531 1.491

6.  Encontrar valor máximo, mínimo y rango.
 Valor máximo: 1.617
 Valor mínimo: 1.408
 Rango: 0.209

7.  Max: 1.617
 Min:1.408
 1.617-1.408= 0.209
 0.209 es el rango.

8.  El numero de intervalos que usaremos será 12.
 Otra forma de sacarlo seria la raíz del numero de datos, que es
igual a 17 o 18.

9. Denominar el tamaño del intervalo, el cual se obtiene de división
de rango entre el numero de intervalos
0.01741667
Lo redondeamos y solo tomamos tres decimales.
0.017

10.  Obtendremos nuestros intervalos aparentes, elegimos el valor
igual o menor al mínimo y se vamos sumando el rango hasta
completar nuestros 12 intervalos.

11. 1 1.408
2 1.425
3 1.442
4 1.459
5 1.476
6 1.493
7 1.510
8 1.527
9 1.544
10 1.561
11 1.578
12 1.595

12. 1.408 1.424
1.425 1.441
1.442 1.458
1.459 1.475
1.476 1.492
1.493 1.509
1.510 1.526
1.527 1.543
1.544 1.560
1.561 1.577
1.578 1.594
1.595 1.611

13.  Ya como ultimo paso nadamas checamos los primeros datos el primer dato tiene que ser menor
que el mínimo.
 el ultimo dato del los inferiores tiene que ser menor o = al máximo para hacer.
 los superiores tenemos restarle una decima al segundo de los inferiores así como les había
explicado antes.
 Para saber si también el limite superior que hice esta bien el ultimo tiene que ser mayor o = al
máximo si da menos no esta bien y tenemos que empezar de nuevo con otra cifra.

14.  Así terminamos con una breve explicación de cómo hacer los
intervalos aparentes
 Espero que les ayude un poco a entender la estadística.

15. laura.anguiano@hotmail.com
http://lau-estadistica.bligoo.com.mx
Gracias por su atención.