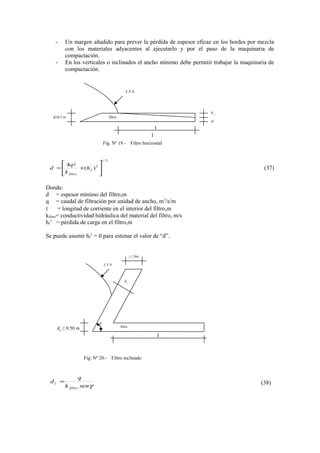
Este documento proporciona información sobre el diseño de presas de tierra. Explica los criterios de diseño geométrico como la altura de la presa, el ancho de la corona, los taludes y las bermas. También cubre los materiales de relleno y la protección del paramento. Proporciona tablas con valores de referencia para los taludes y materiales de relleno según el tipo de presa y embalse. El objetivo es diseñar una presa estable y segura considerando factores geotécnicos, hidrológicos e hidr

1. UNIVERSIDAD NACIONAL DE CAJAMARCA
FACULTAD DE INGENIERIA
CARRERA PROFESIONAL DE INGENIERIA CIVIL
DISEÑO DE PRESAS
MCs. Ing. Francisco Huamàn Vidaurre
Cajamarca, Enero de 2009
Terraplén
(Presa)
Torre de control
Conducto de
descarga
Vertedor
Ràpida
Dren
Conducciòn

2. DISEÑO DE PRESAS DE TIERRA
I. INFORMACION NECESARIA
1.1 Ubicación de la boquilla y del vaso.
Utilizando una carta geogràfica se ubica el eje de la boquilla y el àrea del espejo del
vaso.
1.2 Geologìa de la boquilla y del vaso.
Informe elaborado por un geòlogo acerca de las formaciones geològicas, fallas, napa
freàtica y estabilidad de los taludes tanto del vaso como de la boquilla.
1.3 Topografìa de la boquilla y del vaso.
- Plano topogràfico a curvas de nivel, cada 1.00 m, del vaso y de la boquilla (hasta
300 m aguas abajo del eje).
- Ubicación del eje de la presa en el plano de la boquilla.
1.4 Hidrologìa del proyecto.
- Información climatològica: Velocidad màxima del viento, evaporación diaria o
mensual, temperatura màxima y mìnima.
- Caudales de aporte de la cuenca al 75% y 85% de persistencia.
- Caudales de demanda del proyecto (consumo poblacional, irrigaciòn, pecuario,
hidroenergìa, industrial, etc.)
- Volúmenes del embalse: Volumen muerto, volumen muerto por cota de
derivación, volumen inactivo, volumen ùtil, volumen de super almacenamiento.
1.5 Mecànica de suelos y rocas del material de prèstamo.
El estudio se hace en las canteras en un radio no mayor de 5 km desde la boquilla.
- Clasificaciòn SUCS .
- Pruebas triaxiales (UU, CU, CD)
- Porosidad
- Peso especìfico
- Pruebas de permeabilidad
- Mòdulo de deformaciòn
1.6 Mecànica de suelos y rocas de la boquilla.
- Clasificaciòn SUCS
- Pruebas triaxiales (UU, CU, CD)
- Porosidad
- Peso especìfico
- Pruebas de permeabilidad
- Mòdulo de deformaciòn

3. II. CRITERIOS DE DISEÑO
2.1 DISEÑO GEOMETRICO
2.1.1 Altura de la presa
Inicialmente, la altura de la presa se mide a partir del lecho del cauce en el eje de la
boquilla, tomando en cuenta los niveles caracterìsticos del embalse (cota de derivación,
nivel mìnimo de operación, nivel de aguas màximas ordinarias, nivel de aguas màximas
extraordinarias). Para mayor facilidad se utiliza la gràfica de curvas altura-volumen y
altura-àrea del vaso.
Una vez conocida la cota del NAMO, sobre èsta se incrementa el borde libre. Al fijar la
magnitud total del borde libre de una presa de tierra y enrocamiento han de tenerse en
cuenta el incremento del nivel del embalse por màximas avenidas, el oleaje por viento,
los asentamientos progresivos de la cortina, la pèrdida de altura por deslizamientos o
por rodamiento de partìculas del enrocamiento y el oleaje producido por los sismos.
bl= hm + hv + hr+ ha + hd (1)
Donde:
bl = borde libre, m
hm = altura por marea
D
FV
hm
82.62
2
= (2)
Donde:
V = velocidad del viento, km/h
F = Fetch, km
D = profundidad media del vaso, m
NAMEdelalaenespejodelArea
NAMEdelalahastavol
D
cot
cot.∑=
(3)
hv = altura de la ola por viento, m
hv = 3.22 (V F)1/2
– 26.9 (F)1/4
+ 76 , en cm. (4)
V, en km/h y F, en km.
hr = altura de rodamiento de las olas, producida por el viento, m
)(
3
4
hvhmhr += (5)
ha = asentamiento màximo de la corona, m
El asentamiento de presas de tierra es variable, dependiendo del suelo de sedimentación,
del material del cuerpo de la presa y de su altura. Se han oservado asentamientos desde
25 cm hasta 100 cm durante la construcciòn.

4. hd = altura por màxima avenida probable, m
La altura hd se obtiene del trànsito de avenidas del embalse.
Como referencia, el borde libre en presas es el siguiente:
CUADRO Nº 1.- Valores referenciales de borde libre en presas
Altura de la presa Borde libre
Hasta 15 m 1.5 a 2.0 m
Màs de 15 m hasta 30 m 2.5 a 3.0 m
Màs de 30 m 4.0 a 5.0 m
2.1.2 Ancho de la corona
Se fija este ancho para dar mayor volumen a la presa y aumentar asì su estabilidad, para
tener màs resistencia la coronación contra los deterioros por el oleaje y para establecer
los servicios que sean necesarios sobre la presa.
Es recomendable un ancho mìnimo de 3.0 m para presas de altura inferior a 15.0 m.
Para determinar el ancho de corona, el Bureau of Reclamation sugiere la siguiente
fòrmula:
3
5
+=
H
B (6)
Donde:
B = ancho de la corona, m
H = altura de la presa, m
2.1.3 Taludes
El perfil transversal de una presa de tierra o enrocamiento se determina por los
resultados que proporciona la experiencia, basada en presas existentes y teniendo en
cuenta las otras que fallaron.
El proceso puede ser: dimensionado con arreglo a la experiencia, comprobación de la
estabilidad de sus taludes por las modernas teorìas geotècnicas, previo conocimiento de
los materiales que la van a constituir, y control cuidadoso en la puesta en obra para que
se cumplan las condiciones mìnimas exigidas en la comprobación.
Presas de secciòn homogènea.- Hay materiales que pueden reunir en grado suficiente las
dos condiciones bàsicas de estabilidad e impermeabilidad. El caso màs frecuente lo
constituyen las mezclas bien proporcionadas de gravas y arenas con elementos finos
màs o menos arcillosos (7% - 20% de arcilla). Los suelos de origen morrènico son un
ejemplo tìpico.
Igualmente los limos y ciertos tipos de arcillas, aunque en estos casos se requieren
taludes màs suaves.
CUADRO Nº 2.- Caso de secciòn homogènea, con embalse de regulación o almacenamiento, sin desembalse ràpido.

5. Cortina ubicada en cimentación estable.
Clasificaciòn SUCS Talud aguas arriba Talud aguas abajo
GC, GM, SC, SM 2.5 2
CL, ML 3 2.5
CH, MH 3.5 2.5
CUADRO Nº 3.- Caso de secciòn homogènea, con embalse de regulación o almacenamiento, con desembalse ràpido.
Cortina ubicada en cimentación estable.
Clasificaciòn SUCS Talud aguas arriba Talud aguas abajo
GC, GM, SC, SM 3 2
CL, ML 3.5 2.5
CH, MH 4 2.5
Vaciado ràpido.- Se considera vaciado ràpido al descenso del nivel de agua en el
embalse a razòn de 10 a 15 cm/dìa.
En este caso, el inconveniente en las presas homogèneas el talud de aguas arriba, por ser
poco permeable, no descarga con facilidad las presiones intersticiales remanentes en un
vaciado ràpido y queda trabajando en condiciones peligrosas.
Presas de secciòn zonificada.- Para resolver el inconveniente señalado en las presas
homogèneas y para aprovechar todos los materiales disponibles en la zona de la obra, es
conveniente que las dos zonas exteriores de la secciòn sean suficiente permeables.
CUADRO Nº 4.- Caso de secciòn zonificada, con núcleo mìnimo, embalse para cualquier propòsito,sujeta a
desembalse ràpido no crìtico. Cortina ubicada en cimentación estable.
Clasificaciòn SUCS del
material exterior
Material del núcleo Talud aguas arriba
(H:V)
Talud aguas abajo
(H:V)
No es crìtico; relleno de roca
GW, GP, SW (gravoso) ò SP
(gravoso)
No es crìtico, GC, GM,
SC, SM, CL, ML, CH ò
MH
2:1 2:1
CUADRO Nº 5.- Caso de secciòn zonificada, con núcleo màximo, embalse para regulación o almacenamiento,
no,sujeta a desembalse ràpido . Cortina ubicada en cimentación estable.
Clasificaciòn SUCS del
material exterior
Material del núcleo Talud aguas arriba
(H:V)
Talud aguas abajo
(H:V)
No es crìtico; relleno de roca
GW, GP, SW (gravoso) ò SP
(gravoso)
GC, GM 2:1 2:1
SC, SM 2.25:1 2.25:1
CL, ML 2.5:1 2.5:1
CH, MH 3:1 3.1
CUADRO Nº 6.- Caso de secciòn zonificada, con núcleo màximo, embalse para almacenamiento, sujeta a
desembalse ràpido . Cortina ubicada en cimentación estable.
Clasificaciòn SUCS del
material exterior
Material del núcleo Talud aguas arriba
(H:V)
Talud aguas abajo
(H:V)
No es crìtico; relleno de roca
GW, GP, SW (gravoso) ò SP
(gravoso)
GC, GM 2.5:1 2:1
SC, SM 2.5:1 2.25:1
CL, ML 3:1 2.5:1
CH, MH 3.5:1 3:1
2.1.4 Bermas o banquetas
Tienen por objetivo reducir los efectos de erosión por las lluvias del talud de aguas abajo y en el
talud de aguas arriba para sostener la protecciòn de enrocado.

6. Son útiles para dar acceso a vehìculos, maquinaria y personal tècnico que realizan el
mantenimiento del enrocado y los instrumentos de mediciòn colocados en el cuerpo de la presa.
Pueden tener de 2 a 6 m de ancho y por lo menos debe colocarse una berma bajo el nivel
mìnimo de operación.
2.1.5 Protecciòn del paramento
El paramento de aguas arriba se protege desde el nivel de la corona hasta el nivel mìnimo de
operación. La protecciòn es màs efectiva con rocas durables, grandes y angulares colocadas
sobre un filtro convenientemente graduado. Una regla empìrica para determinar el tamaño de
roca es la siguiente:
M = 103
Hs3
( 7 )
Donde:
M = masa
Hs = altura significativa de la onda, m
Hs = 0.34 F1/2
+ 0.76 – 0.26 F1/4
(8)
Donde:
F = fetch, km
El Bureau of Reclamation ha encontrado que un espesor de 1.0 m del enrocamiento colocado al
volteo es generalmente màs econòmico y satisfactorio para las presas altas (> 30 m). Se usan
espesores menores en las presas bajas.
2.1.6 Materiales de relleno
a) Para el núcleo.- Los materiales deben tener permeabilidad baja ( k < 10 -5
cm/s) y de
forma ideal deben ser de plasticidad intermedia a alta para acomodar la deformación sin
arriesgar el agrietamiento. Ver Tabla 2.5 y Tabla 2.6 del Anexo.
Se ha sugerido que el riesgo de agrietamiento interno severo debido a las
incompatibilidades de deformaciones en las interfaces dentro de la presa sea de
importancia cada vez mayor para rellenos tèrreos, si la razòn entre la sedimentación
màxima después de la construcciòn y H Cotβ, donde H es la altura del relleno y β es el
àngulo del talud, exceda en valores entre 0.003 y 0.005. Es decir:
005.0003.0 y
CotH
>
β
δ
(9)
2
2
Hmv γ
δ =
(10)
Donde:
δ = sedimentación de consolidación primaria
mv = coeficiente de compresibilidad, m2
/kN
γ = peso especìfico del relleno, kN/m3
H = altura de la presa, m
El riesgo de que surjan tales modos de agrietamiento puede moderarse si se efectùa un
cuidadoso y detallado diseño, es decir, evitando grandes irregularidades en las

7. excavaciones de las cimentaciones, el uso de materiales màs hùmedos y màs plàsticos
en el núcleo y la zonificaciòn cuidadosa con transiciones amplias adyacentes al núcleo.
El ancho de la base del núcleo es, en general entre 20 y 40% de la altura del
relleno. En presas < 30 m de altura, un núcleo con ancho del 50% puede ser
insuficiente.
Los suelos màs apropiados para núcleo de presas tienen contenido de arcilla de màs de
25 – 30 %; aunque tambièn pueden utilizarse arenas arcillosas y limos.
b) Para los espaldones.- Los suelos utilizados deben tener una resistencia al corte bastante
grande para permitir una construcción econòmica de taludes estables. Es probable que
el relleno tenga una permeabilidad relativamente alta para ayudar a la disipación de la
presiòn del agua en los poros. Las zonas de los espaldones deben ser de material
progresivamente màs grueso a medida que se aproximan a las caras de los paramentos.
c) Para los filtros.- El material debe estar limpio, permitir el drenaje libre y no ser
propenso a degradaciòn quìmica. Las gravas naturales finas procesadas, rocas trituradas
y arenas gruesas o medias son apropiadas, y se emplean con la secuencia y gradaciòn
determinada por la naturaleza del núcleo y/o los rellenos de los espaldones adyacentes.
El costo de los materiales procesados de filtro es relativamente alto. La permeabilidad
del filtro debe ser, como mìnimo, unas 20 veces superior a la del suelo a proteger y
mejor 50 ò màs.
d) Para los drenes.- Ademàs de los materiales indicados para los filtros, se utilizan gravas
gruesas, rocas, tubos perforados.
Fig. Nº 1.- Presa homogènea con dren chimenea
Fig. Nº 2.- Presa heterogènea con dren chimenea
Fig. Nº 3.- Presa heterogènea con dren horizontal
Fig. Nº4.- Presa heterogènea con transiciones y diafragma
2.2 DISEÑO CONTRA FILTRACION INCONTROLADA
La infiltración dentro y debajo del relleno debe controlarse para prevenir la erosión interna
oculta y la migración de materiales finos. Los gradientes hidràulicos, la presiòn de infiltración y
Filtro-dren
k2
NAMO
L.F.S
Espaldòn de aguas arriba
k1
Espaldòn de aguas
abajo
k1
B/3
B = longitud de la
base
Fundaciòn impermeable ( k << )
H=altura presa
NAMO
B
L.F.S.
Espaldòn
de aguas
arriba
k1
Núcleo
k2
Filtro-dren
k3
Espaldòn de
aguas abajo
k1
Fundaciòn impermeable (k << )NAMO
B
L.F.S.
Espaldòn de aguas
arriba
k1
Núcleo
k2
Espaldòn de
aguas abajo
k3
Fundaciòn impermeable (k << )
NAMO
B
L.F.S.
Espaldòn de
aguas
arriba
k1
>>
Núcleo
k3
Espaldòn
de aguas
abajo
k1
>>
Transición
k2
Transición
k2
Acarreos k4
Nivel
agua
Diafragma
H=altura
presa

8. las velocidades de infiltración dentro y bajo la presa deben, por tanto, restringirse a niveles
aceptables para los materiales empleados.
Fig. Nº5.- Presa heterogènea tubificada
2.2.1 Red de flujo
Uma red de flujo es la soluciòn gràfica de la ecuación de Laplace en dos dimensiones (x,y).
02
2
2
2
=
∂
∂
+
∂
∂
y
h
x
h
(11)
Donde:
h = potencial hidràulico
la que representa la pèrdida de energìa a travès de algun medio resistente, en règimen
permanente.
Cuando un medio tiene las mismas caracterìsticas de conductividad hidràulica en todos sus
puntos se dice que es homogèneo. Si la conductividad hidràulica es la misma en cualquier
direcciòn que se considere, el medio es isòtropo.
Medio homogèneo y anisòtropo: Por ser homogèneo las caracterìsticas de conductividad
hidràulica seràn las mismas en todos sus puntos y por se anisòtropo la conductividad hidràulica
serà distinta segùn la la direcciòn que se considere. Una presa homogènea es anisòtropa debido
a la compactaciòn en capas por lo que su conductividad hidràulica en la direcciòn horizontal es
mayor que en la direcciòn vertical. Una presa heterogènea tiene dos ò màs zonas homogèneas e
isòtropas.
Fig. Nº6.- Red de flujo em uma secciòn de material homogèneo e isòtropo
a
b
Δq
Ψ2
Ψ1
h2
h3
h2
h3
Δh
Lìnea de
filtración
superior
(L.F.S)
Fundaciòn impermeable
Lineas de
corriente (Ψ)
Lineas equipotenciales (h)
Elemento
de una red
de flujo
kx
= ky
NAMO
B
Fundaciòn
impermeable (k << )
Erosión
regresiva

9. En un medio homogèneo e isótropo, líneas de corriente y equipotenciales constituyen una malla
ortogonal que se llama red de flujo. En flujo anisotrópico, sin embargo, la direcciòn de las líneas
de corriente no coincidiràn con la direcciòn normal de las lìneas equipotenciales.
Medio heterogèneo y anisòtropo: Por ser heterogèneo tiene distintas caracterìsticas de
conductividad hidràulica en cada uno de sus puntos, y por ser anisòtropo la conductividad
hidràulica varìa con la direcciòn.
Una presa heterogènea està compuesta por dos ò màs zonas homogèneas y anisotròpicas.
2.2.2 Trazo del la Lìnea de Filtraciòn Superior de una cortina de material homogèneo e
isòtropo
El trazo de la red de flujo requiere conocer previamente la forma y posición de la lìnea de
filtración superior (L.F.S) que atraviesa la cortina, para la geometría propuesta, conociendo las
caracterìsticas de permeabilidad y granulometrìa de los materiales de prèstamo.
Kozeny estudiò el problema de filtración a travès de una cortina homogènea con una cara aguas
arriba parabòlica descansando sobre una superficie impermeable y un dren horizontal
permeable, ambas superficies forman un àngulo α = 180º . Tomando como origen de
coordenadas, de los ejes “x” e “y”, el punto “A” se traza una paràbola B-F-Do, cuya expresión
es :
o
o
y
yy
x
2
22
−
= (12)
La paràbola ingresa al dren formando un àngulo de 90º en el punto “B”

10. Fig. Nº 7.- Paràbola de Kozeny em una presa homogènea e isotrópica com dren hoizontal
La paràbola se corrige, segùn Casagrande, en el punto de entrada “D” por el cual la lìnea ingresa
haciendo un àngulo de 90º con el talud de la cortina, unièndose suavemente en el punto “F”. Ver
la figura Nº7.
El parámetro yo se obtiene segùn:
dhdyo −+= 22
(13)
El dren puede tener otras formas (triangular, exagonal, tipo chimenea, etc.), formando un àngulo
α < 180º entre la superficie impermeable y la permeable.
Fig. Nº 8.- Lìnea de filtración en una presa homogènea e isotrópica con dren inclinado triangular
h
0.3 Δ
Do D
Δ
F
d
A B
yo
= 2 ao
x = (y2
– yo
2
)/2yo
y
x
C
α = 180º
ao
Fundaciòn impermeable Dren
h
0.3 Δ
Do D
Δ
F
d
A
Paràbola de Kozeny
x = (y2
– yo
2
)/2yo
y
x
Fundaciòn impermeable
Filtro dren
triangular
a
Δa
Paràbola
modificada
Vertical
α > 90º

11. En vista de las ventajas de las secciones conformadas de materiales graduados, y de los efectos
benèficos de los filtros-dren al pie del talud de aguas abajo en cortinas homogèneas, las
fronteras de descarga con α > 60º son muy comunes en presas de tierra.
Fig. Nº9.- Lìnea de filtración en una presa homogènea e isotrópica con dren tipo chimenea
Para la modificaciòn de la lìnea de filtración superior (diferentes valores de α ), Casagrande
encontrò la distancia Δa (ver figuras Nº 8 y Nº 9). El valor de a + Δa se conoce trazando la
paràbola de Kozeny.
El valor de Δa se determina conociendo el valor de la relaciòn
aa
a
c
∆+
∆
= (14)
CUADRO Nº 7.- Valores de “c” segùn A. Casagrande
α C Α c α c
30º 0.32 100º 0.24 150º 0.09
60º 0.32 110º 0.21 160º 0.06
70º 0.31 120º 0.18 170º 0.04
80º 0.28 130º 0.16 180º 0.00
90º 0.26 140º 0.13 ----- -----
2.2.3 Trazo de la red de flujo en una cortina homogènea e isòtropa
Una vez definida y dibujada la lìnea de filtración superior se identifican las fronteras, la pèrdida
de carga total (por ejemplo hf de la fig, Nº 10) la cual se divide en cuatro ò màs partes iguales.
A partir de dichas divisiones se trazan lineas horizontales hasta cortar la lìnea de filtración
superior (por ejemplo los punto “P”, “Q”, “R” de la fig. Nº 10). El talud de aguas arriba de la
cortina se considera como la primera lìnea equipotencial y las siguientes se trazan desde los
puntos “P”, “Q” y “R” formando àngulo de 90º tanto con la lìnea de filtración superior como
con las lìneas de corriente.
En la zona de la filtración de trazan dos ò màs tubos de corriente tratando de formar
“cuadrados” con las lìneas equipotenciales.
h
0.3 Δ
Do D
Δ
F
d
A
Paràbola de Kozeny
x = (y2
– yo
2
)/2yo
y
x
Fundaciòn impermeable
Paràbola
modificada
llega tangente a
la frontera
a
Δa
α< 90º

12. Fig. Nº 10.- Red de flujo en una presa homogènea e isotrópica con dren triangular
Después de obtener la red de flujo, es posible determinar el caudal de filtración por unidad de
ancho de cortina (q).
f
d
f
h
N
N
kq = (15)
Donde:
q = caudal de filtración por unidad de ancho, m3
/s/m
k = conductividad hidràulica para material homogèneo e isotròpico, m/s
Nf = nùmero de tubos de corriente
Nd = nùmero de caidas de potencial
hf = pèrdida de carga total, m
El gradiente hidràulico en un elemento de la red de flujo està dado por:
b
h
i
∆
= (16)
Donde:
i = grandiente hidràulico
Δh = caìda de potencial, m
Δh = hf/Nd (17)
b = recorrido mìnimo del agua en el elemento consideraco, m
Ejemplo 1.- En la fig.Nº 10 : k = 2x10-4
m/s, hf = 5.7 m, Nf = 2, Nd = 4. Calcular el caudal de
filtración por metro de cortina y el gradiente hidràulico del “cuadrado” acotado con a= b =
2.52m
Soluciòn:
msmxxq //107.5)7.5(
4
2
)102( 344 −−
=





= (15)
56.0
52.2
4/7.5
==i (16)
hf
Δ h
Δ h
Δ h
Δ h
Dren
k
k
Fundaciòn impermeable
P
Q
R
b
a
1
2
3
4

13. 2.2.4 Transformaciòn de un medio homogèneo y anisòtropo en un medio homogèneo e
isòtropo
En dos dimensiones la conductividad hidràulica en un medio homogèneo y anisòtropo puede
representarse por una elipse de semiejes maxk y mink
Fig. Nº 11.- Conductividad hidràulica en un medio finamente estratificado
En este caso, la variación de la permeabilidad con la direcciòn del flujo sigue la ley elìptica,
indicada en la fig. Nº 11.
Las lìneas de corriente no son ortogonales con las lìneas equipotenciales en un medio
anisòtropo.
La màxima permeabilidad se produce en la direcciòn de la estratificación y està dada por la
siguiente expresión:
∑
∑=
i
ii
màx
d
dk
k (18)
y la mìnima en la direcciòn perpendicular, dada por:
ii
i
kd
d
k
/
min
∑
∑= (19)
La conductividad hidràulica en cualquier direcciòn se expresa segùn:
min
2
max
2
1
k
Sen
k
Cos
k
σσ
σ
+= (20)
(kmax
)1/2
(kmin
)1/2
σ
d1
d2
d3
dn
k1
k2
k3
kn
Suelo finamente estratificado
anisòtropo.
(kσ
)1/2
ψ1
ψ2
h1
h2
Lìneas de corriente y lìneas equipotenciales no
son ortogonales en un medio anisòtropo.
Elipse direccional

14. La mayorìa de los suelos de cimentación son anisotròpicos. Generalmente, en depòsitos
naturales homogèneos, la conductividad hidràulica en la direcciòn horizontal es mayor que la
vertical.
La transformación de este medio en homogèneo e isòtropo exige la conversión de la elipse en
una circunferencia. Es decir, el problema de la transformación de un medio homogèneo y
anisòtropo en su equivalente homogèneo e isòtropo se reduce a un cambio de escala en una sola
direcciòn. Se puede reducir el eje mayor de la elipse o se puede aumentar el eje mayor.
Fig. Nº 12.- Secciòn transformada de presa homogênea y heterogènea
En presas de tierra kmàx = 9 kmin a 10 kmin para núcleo (zonas de baja permeabilidad); kmax = 20kmin
a 25 kmin para los paramentos y depòsitos muy uniformes de materiales gruesos con finos (GC y
GM, segùn la clasificaciòn SUCS). En depòsitos muy erràticos la relaciòn puede alcanzar hasta
un valor de 100.
kmax
= 10 kmin
k
y
x
y
x’
Secciòn real de presa homogènea Secciòn transformada
1
2 1
3
4
kmax
=20kmin
kmax
=10kmin
kmax
=20kmin
kmax
=25kmin
kmax
=50kmin
y
x
Secciòn real de presa heterogènea
k1
k2
k1
k3
k4
y
x’
Secciòn transformada de presa heterogènea
1
2 1 3
4

15. Las dimensiones geomètricas de la secciòn transformada de una presa se halla con cualquiera de
las dos expresiones siguientes:
max
min
'
k
k
xx = (21)
ò
min
max
'
k
k
yy = (22)
Realizada la transformación de escala en la direcciòn X ò en la direcciòn Y, la conductividad
hidràulica global o equivalente para cada medio serà:
minmax .kkk = (23)
Ejemplo 2.- Hallar las acotaciones de la secciòn transformada y la permeabilidad global de
cada medio de la presa heterogènea indicada en la fig.Nº 13, para la siguiente información:
Medio kmax/kmin kmax
(cm/s)
1 20 5x10-4
2 10 7x10-6
3 25 2x10-3
4 50 3x10-2
L1
(m)
L2
(m)
L3
(m)
L4
(m)
L5
(m)
L6
(m)
L7
(m)
L8
(m)
L9
(m)
31.0 24.0 34.2 26.3 17.5 27.1 10.2 10.0 10.0
Soluciòn:
El cambio de escala se harà en la direcciòn horizontal. Las dimensiones verticales no varìan.
L1 = 31.0 m
De acuerdo a la expresión (21) se tiene:
L2 = 24.0 (1/20)1/2
= 5.36 m
L3 = 34.2 (1/20)1/2= 7.65 m
L4 = 26.3 (1/10)1/2
= 8.32 m
L5 = 17.5 (1/20)1/2
= 3.91 m
L6 = 27.1 (1/20)1/2
= 6.06 m
L7 = 10.2 (1/25)1/2
= 2.04 m
L8 = 10.0 m
L9 = 10.0 m
1
2 1
3
4
y
x
Fig. Nº 13.-Secciòn real de la presa heterogènea del ejemplo 2
L1 L2 L3 L4 L6
L9
L5
L8
L7

16. La permeabilidad global para cada material de la presa se determina con la expresión (23).
( ) scmxk /101.110(
20
5
)10(5 2)44
1
−−−
=





=
k2 = 2.2 x 10-3
cm/s
k3 = 1.3 x 10-2
cm/s
k4 = 4.2 x 10-2
cm/s
2.2.5 Trazo de la red de flujo en una cortina heterogènea
Inicialmente, se dibuja la secciòn transformada de la cortina. Luego se traza la lìnea de filtración
superior y se determina la permeabilidad global de cada zona.
Puesto que el dominio de flujo consta de dos ò màs porciones de diferente permeabilidad, la red
de flujo se distorsiona en las fronteras entre los diversos materiales, utilizando la teoría del flujo
en regiones compuestas.
Fig. Nº 14.- Condiciones de transferencia de la lìnea superior de flujo en la frontera de suelos
con permeabilidades diferentes.
Las condiciones de transferencia de la lìnea de filtración superior en la frontera de suelos con
materiales diferentes se indican en la fig. Nº 14.
k1
> k2
k1
ω
β
k2
α k1
< k2
k1
k2
ω
k1
> k2
α
β
ω
k1
k2
k1
< k2
α
β
ω k2
k1
Vertical
ω
k1
k2
α = β α = β = 0
β = 270º - α - ω β = 270º - α - ω (caso excepcional)
Discontinuidad (caso usual)

17. Fig. Nº 15.- Red de flujo en una presa heterogènea
En un tubo de corriente de la fig. Nº 15 el caudal se puede expresar por cualquiera de la dos
formas siguientes:
1
1
1 a
b
h
kq
∆
=∆ (24)
2
2
2 a
b
h
kq
∆
=∆ (25)
Igualando las expresiones (24) y (25) y sabiendo que a1 = b1, se obtiene la relaciòn:
2
2
1
2
a
b
k
k
= (26)
Por ejemplo si k2= 2 k1, entonces b2 = 2 a2. Es decir, los elementos de la red de flujo de la zona 2
son rectàngulos en la relaciòn 1:2.
2.2.6 Resistencia a la Falla por Filtraciòn
La resistencia a la falla por filtración es la capacidad que posee el material o suelo de oponer
resistencia al surgimiento de deformaciones de su componente sòlido debido a la tubificaciòn,
erosión por contacto y reventón.
El agua que fluye a travès de un cuerpo poroso, ejerce sobre las partìculas de èste una fuerza por
unidad de volumen, en la direcciòn del gradiente hidràulico. Dicha fuerza se denomina fuerza
de filtración, que tiene direcciòn perpendicular a las lìnaes equipotenciales de la red de flujo.
La fuerza por unidad de volumen ejercida por el agua en la direcciòn del flujo se expresa por:
ωγ
b
h
j
∆
= (27)
Donde:
j = fuerza por unidad de volumen
i = Δh/b = gradiente hidràulico
γω = peso especìfico del agua
El suelo resiste esta acciòn, por una parte, mediante las fuerzas de cohesión entre partìculas y,
por otra, gracias al soporte que a cada partícula le brindan las que se encuentran aguas abajo de
ella. El componente del peso del suelo en la direcciòn del flujo puede actuar a favor o en contra
del arrastre de pertìculas, segùn la direcciòn de aquel con respecto a la vertical.
En un dominio de flujo homogèneo, las partìculas localizadas sobre la superficie de salida del
flujo se encuentran màs expuestas al arrastre por las fuerzas de filtración. Màs aùn, ciertas
irregularidades, como una pequeña cavidad en la cara de salida, crean concentraciones de flujo
hf
Δ h
Δ h
Δ h
Δ h
k1
k1
Fundaciòn impermeable
b1
a1
1
2
3
4
a2
b2
k2
k2
Δq

18. que aumentan la tendencia a dicho arrastre. Un proceso de erosión iniciado en el lado de aguas
debajo de una presa (sobre el talud o en la cimentación) puede progresar de esta manera hacia el
embalse en la forma de un ducto ò tubo (fenómeno de tubificaciòn).
Los estudios sobre presas tubificadas han demostrado que la propiedad màs importante de un
material en cuanto a su resistencia a la tubificaciòn es el ìndice de plasticidad.
El factor de seguridad (FS)tub contra la tubificaciòn, para material no cohesivo, en cada
“cuadrado” de la red de flujo està dado por:
)1(
1
)(
ei
FS s
tub
+
−
=
γ
(28)
Donde:
(FS)tub = factor de seguridad contra la tubificaciòn de material granular, adimensional
γs = gravedad especìfica de las partìculas minerales del material (2.65 a 2.75), adimensional
e = ìndice de vacìos del material, adimensional
Se acepta generalmente que (FS)tub sea mayor igual que 5.
Los estudios sobre presas tubificadas han demostrado que en los suelos existe un amplìsimo
margen de susceptibilidad al fenómeno; las propiedades de los suelos, especialmente la
plasticidad de sus finos ejercen gran influencia, incluso mayor que la compactaciòn.
CUADRO Nº 8.- Grado de resistencia a la tubificaciòn en diferentes suelos.
Gran resistencia
a la tubificaciòn
1. Arcillas muy plàsticas (Ip > 15%), bien compactadas.
2. Arcillas muy plàsticas (Ip > 15%), con compactaciòn
deficiente.
Resistencia
media a la
tubificaciòn
3. Arenas bien graduadas o mezclas de arena y grava,
con contenido de arcilla de plasticidad media (Ip >
6%), bien compactadas.
4. Arenas bien graduadas o mezclas de arena y grava,
con contenido de arcilla de plasticidad media (Ip >
6%), deficientemente compactadas.
5. Mezclas no plàsticas bien graduadas y bien
compactadas, de grava, arena y limo (Ip < 6%).
Baja resistencia
a la tubificaciòn
6. Mezclas no plàsticas bien graduadas y
deficientemente compactadas, de grava, arena y limo
(Ip < 6%).
7. Arenas limpias, finas, uniformes (Ip < 6%), bien
compactadas.
8. Arenas limpias, finas, uniformes (Ip < 6%),
deficientemente compactadas.
Los filtros graduados son la mejor defensa contra la tubificaciòn sea en la etapa de proyecto o
en la de poner remedio a un mal ya presente.
2.2.7 Filtros
En una presa de tierra, conviene que el paramento de aguas abajo sea lo màs permeable posible,
para que la lìnea de saturación (L.F.S.) después de atravesar el núcleo, baje con rapidez y el
paramento quede libre o casi libre de presiones internas.
Los materiales comunes utilizados en los paramentos son del propio cauce o de las terrazas
fluviales, en donde predominan las gravas y arenas.

19. Basta una relaciòn de permeabilidades de 1/100 para que sea efectivo el drenaje entre dos
medios. Cuando no es asì, habrà que intercalar entre el núcleo y el paramento un dren. Este
deberà estar protegido por filtros, tanto del lado del núcleo como del paramento, salvo que del
lado del paramento se cumpliera la condiciòn de filtro. Cuando el espaldòn es permeable, èl
mismo sirve de drenaje y sòlo falta un filtro entre èl y el núcleo.
Es deseable que el paramento de aguas arriba sea tambièn permeable, para que sus presiones
internas sigan con relativa rapidez las oscilaciones del embalse. Se puede colocar un filtro aguas
arriba del núcleo.
Fig. Nº 16.- Ubicación de un filtro
Un filtro deja pasar el agua sin lavado de los finos de la presa. Su funciòn es darle estabilidad al
núcleo. Los filtros no solo impiden la transmigraciòn de finos, sino que actùan de forma
inducida sobre el núcleo y zonas de finos haciendo que se cierren las fisuras que se forman en
las zonas con materiales cohesivos finos.
Los filtros deben colocarse en toda zona en la que se encuentren en contacto materiales de
granulometrìa muy diferentes y haya riesgo de paso de finos de uno a otro. Los filtros que son
atravesados por lìneas de corriente con componentes que tienden a favorecer la migración de
finos, se llaman crìticos, porque su fallo repercute directamente en la estabilidad de la presa. Se
considera crìtico el que està aguas abajo del núcleo.
La permeabilidad del filtro debe ser, como mìnimo, unas 20 veces superior a la del suelo a
proteger.
2.2.8 Normas para el proyecto de filtros
El parámetro màs significativo es el diámetro D15 de las partìculas del filtro que son iguales o
menores que el 15% del total. Otro parámetro es el diámetro d85 de las partìculas del suelo
base, iguales o menores que el 85% del total. Los porcentajes estàn referidos al peso.
a) Condiciòn de la capacidad de retenciòn:
5
85
15
<
d
D
(varìa de 4 a 9, segùn los suelos) (29)
Cuando los suelos impermeables incluyen gravas, èstas no deben tenerse en cuenta en el
còmputo, y las normas se aplicaràn sòlo a los materiales que pasan por el tamiz 4, excepto para
los suelos del grupo 3.
Para aplicar estas normas se han dividido los suelos en cuatro grupos:
(Granulometrìa
fina)
- Núcleo
Paramento homogèneo
Cimiento
Otra zona cualquiera
FILTRO
Capas progresivas.
Puede ser una sola capa.
Granulometrìa gruesa
Flujo

20. Fig. Nº 17.- Paràmetros filtro - suelo
GRUPO 1 : Arcillas y limos finos.
Son los suelos base que tienen màs del 85% de materiales que pasan por el tamiz 200. El filtro
debe cumplir la condiciòn:
85915 dD ≤ (30)
GRUPO 2 : Arcillas o limos arenosos y arenas arcillosas o limosas.
Son los suelos con un 40% a un 85% màs fino que el tamiz 200. El filtro debe cumplir la
condiciòn:
mmD 7.015 ≤ (31)
En estos suelos predomina la influencia de los finos en las pruebas sobre los filtros, y no
influyen las partìculas de arena.
En los filtros de los grupos 1 y 2 debe predominar la porciòn arenosa sobre la grava.
GRUPO 3 : Arenas y gravas arenosas impermeables con bajo contenido de finos.
Son suelos con menos del 15% màs fino que el tamiz 200 de la norma ASTM (0.074 mm). El
filtro debe cumplir:
85415 dD ≤ (32)
El criterio debe aplicarse a la totalidad del suelo, sin excluir las gravas.
GRUPO 4 : Suelos intermedios entre los grupos 2 y 3.
Son los que dan entre el 15% y el 40% de elementos que pasan por el tamiz 200. El filtro debe
cumplir:
( )mmd
P
D 7.0854
25
40
15 −
−
≤
(33)
Donde P es el porcentaje de elementos que pasan por el tamiz 200.
Los cuatro grupos de suelos incluyen todos los usuales en las partes impermeables de las presas
de materiales sueltos.
Para los grupos 1 y2 las normas se aplican con independencia de la forma de la curva
granulomètrica.
% en peso que pasa
Diàmetro
100
85
15
D85
Filtro
d85
Suelo
D15 d15
5

21. Para los grupos 3 y4 se aplican a suelos con una curva de distribución razonablemente
graduada; cuando èsta presenta fuertes discontinuidades, es aconsejable dimensionar el filtro
para la porciòn màs fina de la curva, o bien hacer ensayos directos en laboratorio.
b) Capacidad de drenaje del filtro:
Debe cumplirse lo siguiente:
k filtro ≥ 50 a 100 veces k suelo (34.1)
El k filtro se puede estimar con la siguiente expresión:
k filtro = 100 (D10 )2
(e min)2
(34.2)
Donde:
D10 = tamaño de partícula correspondiente al 10% em peso del material que pasa el tamiz, cm
e min = relaciòn de vacìos para material compactado
D 15filtro ≥ 5 d15 suelo (35)
2.2.9 Estabilidad interna del filtro
Se hace la siguiente prueba;
- Se elige un diámetro Dx al que corresponde x% de elementos màs finos que èl.
- Dividir la curva de distribución granulomètrica del material en dos partes arbitrarias y
tratarlas cono si la màs fina (F) fuera un suelo base y la màs gruesa (G) un filtro.
- Calcular el coeficiente de estabilidad interna (IR), mediante la siguiente expresión:
5
)15(
)(85
)(15
<
+
==
DY
YD
FD
GD
IR
(36)
Fig. Nº 18.- Granulometrìa para estabilidad interna del filtro
Para obtener DY, primero se obtiene X% y luego se ingresa con 0.85X% para obtener DY.
Luego a Y% se le agrega 15% en la escala vertical dando (Y+15)% con el cual se ingresa para
salir con D(Y+15).
En ensayo se repite para varios puntos X, por ejemplo con intervalos de 5%.
2.2.10 Espesor del filtro
Està determinado por las siguientes condiciones:
- El necesario para cumplir su funciòn, de forma que la interface de penetración inicial
ocupe sòlo una proporción reducida del espesor.
100 %
(Y+15)%
X %
Y=0.85X%
DY D(Y+15)
DX
0%
% en peso que pasa

22. - Un margen añadido para prever la pèrdida de espesor eficaz en los bordes por mezcla
con los materiales adyacentes al ejecutarlo y por el paso de la maquinaria de
compactaciòn.
- En los verticales o inclinados el ancho mìnimo debe permitir trabajar la maquinaria de
compactaciòn.
Fig. Nº 19.- Filtro horizontal
2/1
2'
)(
4








+= f
filtro
h
k
q
d

(37)
Donde:
d = espesor mìnimo del filtro,m
q = caudal de filtración por unidad de ancho, m3
/s/m
‫׀‬ = longitud de corriente en el interior del filtro,m
kfiltro= conductividad hidràulica del material del filtro, m/s
hf’ = pèrdida de carga en el filtro,m
Se puede asumir hf’ = 0 para estimar el valor de “d”.
Fig. Nº 20.- Filtro inclinado
γsenk
q
d
filtro
=1 (38)
L.F.S.
d≥0.5 m
‫׀‬
‫׀‬
h’f
d’
filtro
L.F.S.
d2
≥ 0.50 m filtro
d1
γ
≥ 1.0m
‫׀‬

23. 2/1
2
4








=
filtrok
q
d

(39)
Ejemplo 3.- Dimensionar el espesor de un filtro inclinado γ = 75º , ‫׀‬=35.0 m, q = 0.0085
m3
/s/m, kx = 0.18 m/s, kx/ky = 20.
Soluciòn:
( ) 





=
20
18.0
18.0filtrok = 0.0402 m/s (23)
( )( )
m
sen
d 22.0
º750402.0
0085.0
1 ==
(38)
Se adopta un valor mayor recomendado segùn la fig.Nº 20:
d1 = (1.0) (sen 75º) = 0.97 m
md 44.5
0402.0
)35()0085.0()4(
2 ==
(39)
Ejemplo 4.- Verificar la capacidad de retenciòn y drenaje del filtro de una presa homogènea ,
(suelo Grupo 1) ubicada en un lecho aluvial (suelo Grupo 3). Se cuenta con la siguiente
información:
kxpresa = 6x10-7
m/s
kxcimentaciòn = 10-3
m/s
kxfiltro = 0.18 m/s
D15 filtro = 2.76 cm
d15 presa = 1.25x10-4
cm
d15 cimentaciòn = 0.04 cm
d85 presa = 0.113 cm
d85 cimentaciòn = 1.92 cm
Soluciòn:
a) presa-filtro
- Capacidad de retenciòn
2.76 > 1.017 (no cumple) (30)
- Capacidad de drenaje
0.18 > 3x10-5
a 6x10-5
(cumple) (34)
2.76 > 6.25x10-4
(cumple) (35)
b) cimentación-filtro
- Capacidad de retenciòn
2.76 < 7.68 (cumple) (32)
- Capacidad de drenaje
0.18 > 5x10-2
a 10-1
(cumple) (34)
2.76 > 0.2 (cumple) (35)

24. Entre el material de la presa y el filtro se colocarà una capa de transición que cumpla las
condiciones de retenciòn y drenaje. Lo mismo de debe cumplir entre la transición y el filtro
graduado.