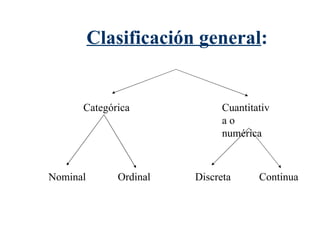
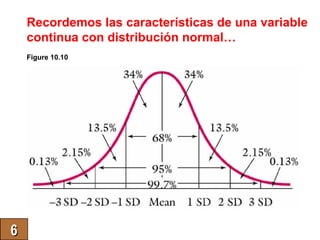
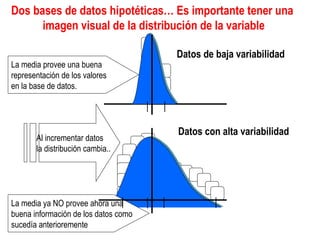
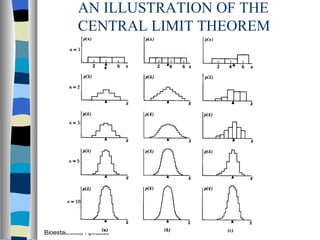
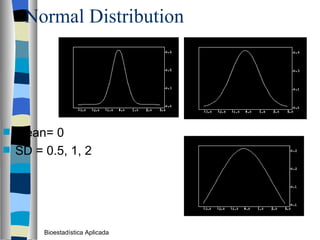
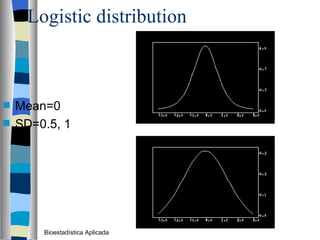
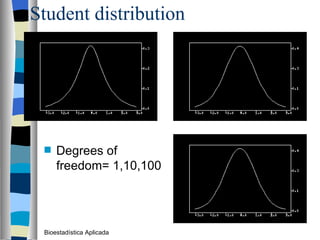
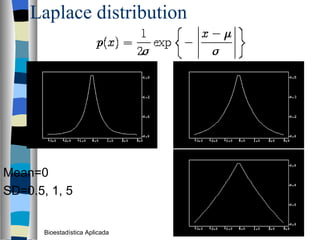
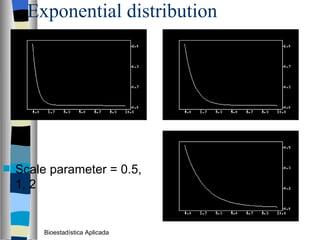
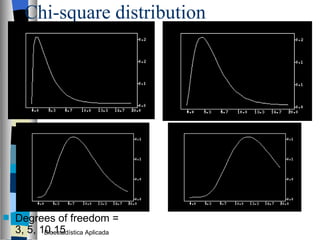
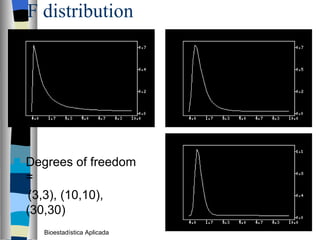
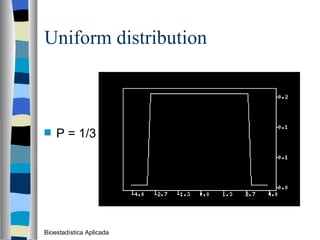
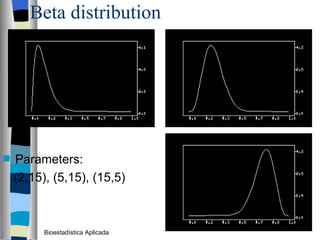
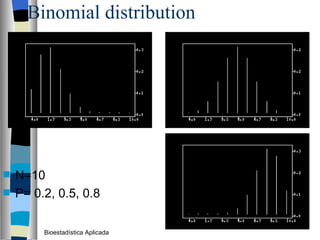
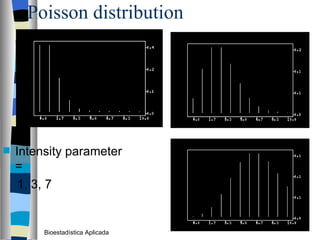
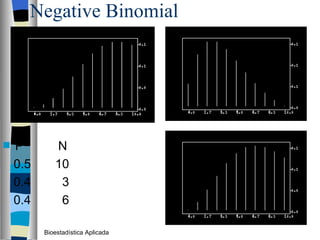
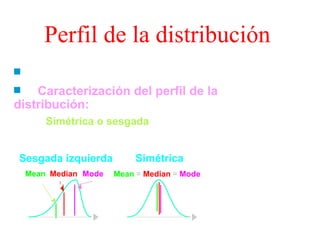
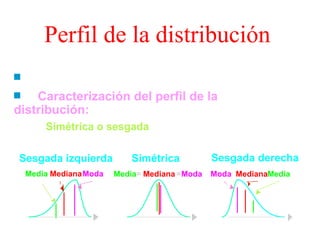
El documento trata sobre conceptos básicos de bioestadística como variables continuas y discretas, distribuciones de probabilidad como la normal y binomial, y el teorema del límite central. Explica que las variables continuas son independientes de cómo se miden y que al discretizar se pierde información. También describe diferentes distribuciones de probabilidad como la normal, exponencial y binomial y sus parámetros.

1. Bioestadística PROGRAMA DE DOCTORADO EN SALUD PÚBLICA

2. Contactos Mirko Zimic Jefe de la Unidad de Bioinformática y Biología Computacional, Facultad de Ciencias, UPCH 3190000 anexo 2604 [email_address] [email_address] http://www.upch.edu.pe/facien/dbmbqf/docentes.htm http://www.abeperu.net/

3. Summarizing The ‘randomness’ of a random variable resides on: The variability of the initial conditions The dynamical instability The perturbation suffered during a measurement

4. Important Conclusion: Determinism and Random Behavior are not actually divorced, but they are connected through the Dynamical Equations. Therefore, Random Behavior is a consequence of determinism under special conditions

5. Clasificación general : Categórica Cuantitativa o numérica Nominal Ordinal Discreta Continua

6. Las variables continuas El carácter continuo de una variable lo da la naturaleza intrínseca del observable físico y es independiente de la manera cómo se mida (i.e. del instrumento utilizado) ó de la manera cómo se reporte la medición

7. Efecto de la manera ‘cómo se mide’ una variable Imaginemos que medimos la induración del PPD en varios pacientes, y para ello utilizamos una regla milimetrada. Las dimensiones medidas para diferentes personas fueron: 5mm, 12mm, 9mm, 32mm, 21mm Aparentemente estamos frente a una variable discreta, aunque en realidad la induración (longitud) es y debe tratarse de manera continua.

8. Categorización/discretización : Las variables continuas pueden ser convertida en variables discretas y hasta en categóricas En este proceso se pierde información (precisión) La información debe obtenerse al mayor nivel de precisión posible y luego agruparse si fuera necesario (discretización)

9. Perfil de la distribución Describe cómo los Datos están Distribuídos Caracterización del perfil de la distribución: Simétrica o sesgada

10. Recordemos las características de una variable continua con distribución normal… Figure 10.10 6

11. Dos bases de datos hipotéticas… Es importante tener una imagen visual de la distribución de la variable La media provee una buena representación de los valores en la base de datos. Datos de baja variabilidad Datos con alta variabilidad La media ya NO provee ahora una buena información de los datos como sucedía anterioremente Al incrementar datos la distribución cambia..

12. El Teorema del Límite Central da validez a los intervalos de confianza La media de una muestra “grande” de datos de cualquier tipo sigue una distribución normal Esto aún se cumple para datos binomiales (sexo, prevalencia, sensibilidad, etc) Qué es una muestra grande? Eso varía según cada tipo de dato (entre otras cosas) A medida que el tamaño de muestra crece, la distribución de la media muestral se hace más normal

13. AN ILLUSTRATION OF THE CENTRAL LIMIT THEOREM Bioestadística Aplicada

14. Continuous Models on the Line Normal Logistic Cauchy Laplace Student Non-central Student Bioestadística Aplicada

15. Normal Distribution Mean= 0 SD = 0.5, 1, 2 Bioestadística Aplicada

16. Logistic distribution Mean=0 SD=0.5, 1 Bioestadística Aplicada

17. Student distribution Degrees of freedom= 1,10,100 Bioestadística Aplicada

18. Laplace distribution Mean=0 SD=0.5, 1, 5 Bioestadística Aplicada

19. Continuous Models on the Half Line Exponential Gama Chi-square Non central Chi-square F Non central F Weibull Bioestadística Aplicada

20. Exponential distribution Scale parameter = 0.5, 1, 2 Bioestadística Aplicada

21. Chi-square distribution Degrees of freedom = 3, 5, 10,15 Bioestadística Aplicada

22. F distribution Degrees of freedom = (3,3), (10,10), (30,30) Bioestadística Aplicada

23. Continuous Models on a Finite Interval Beta Uniform Bioestadística Aplicada

24. Uniform distribution P = 1/3 Bioestadística Aplicada

25. Beta distribution Parameters: (2,15), (5,15), (15,5) Bioestadística Aplicada

26. Discrete Models Binomial Poisson Negative Binomal Uniform Bioestadística Aplicada

27. Binomial distribution N=10 P= 0.2, 0.5, 0.8 Bioestadística Aplicada

28. Poisson distribution Intensity parameter = 1, 3, 7 Bioestadística Aplicada

29. Negative Binomial P N 0.5 10 0.4 3 0.4 6 Bioestadística Aplicada

30. Distribuciones sesgadas

31. Perfil de la distribución (skewness coefficient) Describe cómo los Datos están Distribuídos Caracterización del perfil de la distribución: Simétrica o sesgada

32. Perfil de la distribución Describe cómo los Datos están Distribuídos Caracterización del perfil de la distribución: Simétrica o sesgada Sesgada izquierda Simétrica Mean = Median = Mode Mean Median Mode

33. Perfil de la distribución Describe cómo los Datos están Distribuídos Caracterización del perfil de la distribución: Simétrica o sesgada Sesgada derecha Sesgada izquierda Simétrica Media = Mediana = Moda Media Mediana Moda Mediana Media Moda

34. Análisis de OUTLIERS: Datos sesgados: Valores que se exceden de 3 rangos intercuartiles por debajo del primer cuartil Q1 o por encima del tercer cuartil (Q3) (percentiles 25 y 75 respectivamente) Sesgada izquierda Sesgada Positiva Q 1 – 3(Q 3 – Q 1 ) Q 1 Q 3 Q 1 Q 3 Q 3 + 3(Q 3 – Q 1 ) outlier region outlier region

35. Uso de la Teoría de Propagación Errores Se aplica cuando tenemos una o muy pocas mediciones y deseamos presentar un rango de variabilidad en nuestras conclusiones Bioestadística Aplicada