Este documento presenta ejercicios sobre grafos y dígrafos. Incluye encontrar la matriz de adyacencia y de incidencia de un grafo, determinar si es conexo, regular, completo, euleriano o hamiltoniano. También incluye encontrar una cadena y un ciclo en un grafo y dígrafo, construir un árbol generador, y calcular distancias en un dígrafo usando el algoritmo de Dijkstra.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD FERMIN TORO
FACULTAD DE INGENIERIA
CABUDARE ESTADO LARA
Ejercicios Propuestos
Grafos y Dígrafos
.
Alumno: Jonathan Bastidas
C.I. 17.048.561
Cabudare, Junio 2012

2. Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo?. Justifique su respuesta
d) Es simple?. Justifique su respuesta
e) Es regular?. Justifique su respuesta
f) Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano
v6
v4
v5
v8
v7
a) Matriz de adyacencia
Ma (g)=
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0

3. b) Matriz de incidencia
Mi (g)=
V1 V2 V3 V4 V5 V6 V7 V8
A1 1 1 0 0 0 0 0 0
A2 1 0 1 0 0 0 0 0
A3 0 1 1 0 0 0 0 0
A4 1 0 0 1 0 0 0 0
A5 1 0 0 0 0 0 1 0
A6 1 0 0 0 0 0 0 1
A7 0 0 1 0 0 1 0 0
A8 0 1 0 0 1 0 0 0
A9 0 1 0 0 0 0 0 1
A10 0 1 0 0 0 1 0 0
A11 0 0 1 1 0 0 0 0
A12 0 0 1 0 0 0 1 0
A13 0 0 1 0 1 0 0 0
A14 0 0 0 1 1 0 0 0
A15 0 0 0 1 0 0 1 0
A16 0 0 0 0 1 1 0 0
A17 0 0 0 0 1 0 1 0
A18 0 0 0 0 0 0 1 1
A19 0 0 0 0 1 0 0 1
A20 0 0 0 0 0 1 0 1
c) Es conexo?. Justifique su respuesta
Si es conexo, porque todos los vértices se encuentran conectados por aristas. Están
conectados entre sí. Existe una cadena.
d) Es simple?. Justifique su respuesta
Es simple ya que no contiene lazos a demás entre cada par de vértices no hay más de una
arista que los conecte.
e) Es regular?. Justifique su respuesta
No es regular, porque los vértices tienen distintos grados
V1, V2, V7 y V8 tiene grado 5.
V3 y V5 tienen grado 6.
V4 y V6 tienen grado 4.

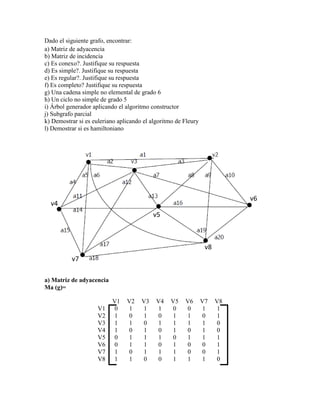
4. f) Es completo? Justifique su respuesta
No es completo, porque posee aristas paralelas y más de una arista por cada par de vértices,
todos no se conectan entre si, Como: v1 y v6, v2 y v4.
g) Una cadena simple no elemental de grado 6
C = [ v3,a7,v6,a16,v5,a14,v4,a15,v7,a17,v5,a8,v2]
h) Un ciclo no simple de grado 5
C= [ v3,a3,v2,a10,v6,a20,v8,a19,v5,a8,v2,a3,v3]
i) Árbol generador aplicando el algoritmo constructor
Paso 1: Seleccionamos el vértice v1, H1= {v1}
Paso 2: Seleccionamos la arista a1 y H2= {v1, v2}
Paso 3: seleccionamos la arista a3 entonces H3= {v1, v2, v3}
Paso 4: seleccionamos la arista a11 entonces H4= {v1, v2, v3, v4}

5. Paso 5: seleccionamos la arista a15 entonces H5= {v1, v2, v3, v4, v7}
Paso 6: seleccionamos la arista a17 entonces H6= {v1, v2, v3, v4, v7, v5}

6. Paso 7: seleccionamos la arista a19 entonces H7= {v1, v2, v3, v4, v7, v5, v8}
Paso 8: seleccionamos la arista a20 entonces H7= {v1, v2, v3, v4, v7, v5, v8, v6}

7. j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
No es eureliano, aplicando el algoritmo de Fleury se puede visualizar que el grafo
no es Eureliano ya que no es posible que no se repitan las aristas en el recorrido.
No existe una trayectoria euleriana porque el grafo tiene más de dos vértices de
orden impar
l) Demostrar si es hamiltoniano
Si es hamiltoniano porque el ciclo toca todos sus vértices.

8. Dado el siguiente dígrafo
a) Encontrar matriz de conexión
b) Es simple?. Justifique su respuesta
c) Encontrar una cadena no simple no elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
a) Encontrar matriz de conexión
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0

9. b) Es simple?. Justifique su respuesta
Si es Simple, debido a que no existen lazos en ningún vértice ni tampoco arcos paralelos.
c) Encontrar una cadena no simple no elemental de grado 5
C= v2, a2, v3, a7, v5, a10, v2, a2, v3, a8, v4
d) Encontrar un ciclo simple
C= v2, a4, v6, a14, v5, a10, v2
e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
M=
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 1 0 1
0 0 0 0 1 0
M2 =
0 0 1 1 1 1
1 0 0 1 1 1
1 1 0 1 0 1
0 1 1 0 1 0
1 0 1 1 1 1
0 1 0 1 0 1
M3 =
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
0 1 1 1 1 1
0 1 1 1 1 1
1 0 1 1 0 1

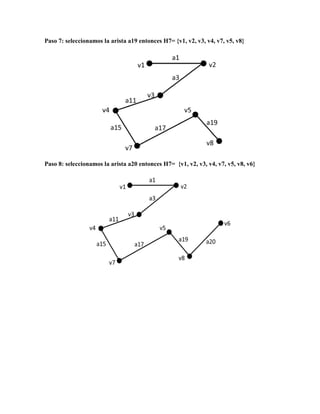
10. M4 =
1 1 1 1 1 1
1 0 1 1 1 1
0 1 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
M5 =
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
In
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Acc= bin [I6+M+M2+M3+M4+M5]
3 4 5 4 5 4
4 2 5 5 5 5
3 4 3 4 4 4
4 4 3 5 4 4
3 4 4 5 4 5
3 3 3 4 1 4
Acc(D)=bin
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
Como se pudo observar el dígrafo es fuertemente conexo.

11. f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
Pasos Vértices Datos para el Calculo de Selección
paso a di + 1 v*i + 1
desarrollar
0 V0= [v2] Vo*=v2 D1(v1)= ∞ V1*=V3
Do (vo*)= 0 D1(v3)= 3
Do (v1)= ∞ D1(v4)= 4
Do (v3)= ∞ D1(v5)= ∞
Do (v4)= ∞ D1(v6)= 3
Do (v5)= ∞
Do (v6)= ∞
1 V1= [v2,v1*] V1*=v3 D2(v1)= ∞ V2*=v4
D1(v1*)=3 D2(v4)=4
D1(v1)= ∞ D2(v5)=7
D1(v4)=4 D2(v6)= ∞
D1(v5)= ∞
D1(v6)=3
2 V2=[v2,v3,v2*] V2*=v4 D3 (v1)=8 V3*=v6
D2(v2*) =4 D3(v5)= ∞
D2(v1)= ∞ D3(v6)=6
D2(v5)= 4
D2(v6)= 7
3 V3=[v2,v3,v4,v3*] V3*=v6 D4(v1)= ∞ V4*=v1
D3(v3*)=6 D4(v5)= ∞
D3(v1)=8
D3(v5)= ∞
4 V4=[v2,v3,v4,v6,v4*] V4*=v5 D5(v1)=15 V5*=v1
D4(V4*)= ∞
D4(v1)= ∞
5 V5=[v2,v3,v4,v6,v5*]
Las distancias son:
Dist (v2, v3)=3
Dist (v2, v4) =4
Dist (v2, v6) =6
Dist (v2, v5) =∞
Dist (v2, v1) =15