Este documento presenta una serie de ejercicios propuestos sobre grafos. En el primer ejercicio, se pide encontrar la matriz de adyacencia y de incidencia de un grafo dado, determinar si es conexo, simple, regular, completo, y encontrar una cadena, ciclo, árbol generador y subgrafo parcial. En el segundo ejercicio, se pide encontrar la matriz de conexión de un dígrafo dado, determinar si es simple, encontrar una cadena y ciclo, y demostrar si es fuertemente conexo.

1. UNIVERSIDAD FERMIN TORO
DECANATO DE INGENIERIA
ESCUELA DE COMPUTACION
CABUDARE – EDO. LARA
Integrante:
-Beatriz Sánchez M CI: 17.196.692
-Profesora: Adriana Barreto
SAIA “A”
Noviembre, 2011

2. Ejercicios Propuestos
1.- Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo? Justifique su respuesta
d) Es simple? Justifique su respuesta
e) Es regular? Justifique su respuesta
f) Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo Parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano
V6 V4
V5
V8
V7

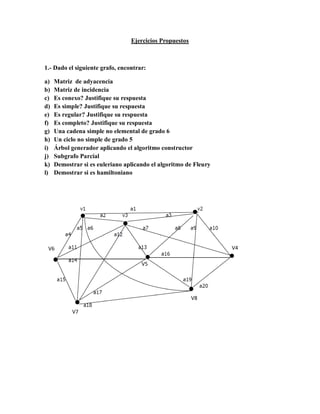
3. a) Matriz de adyacencia
Ma= 0 1 1 0 0 1 1 1
1 0 1 1 1 0 0 1
1 1 0 1 1 1 1 0
0 1 1 0 1 0 0 1
0 1 1 1 0 1 1 1
1 0 1 0 1 0 1 0
1 0 1 0 1 1 0 1
1 1 0 1 1 0 1 0
b) Matriz de incidencia
1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Mi = 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0
0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 1
c) ¿Es conexo? Justifique su respuesta
Sí es conexo ya que se cumple que para todo par de vértices {U, V} se tiene que U y V
están conectados.
d) ¿Es simple? Justifique su respuesta
Sí es Simple, ya que no tiene lazos.
e) ¿Es regular? Justifique su respuesta
No es Regular, ya que no todos los vértices tienen el mismo grado.
f) ¿Es completo? Justifique su respuesta
No es Completo, ya que es un grafo simple que tiene exactamente una arista entre cada
par de vértices distintos.
g) Una cadena simple no elemental de grado 6.
C = [ V7,a18,V8,a9,V2,a8,V5,a13,V3,a12,V7,a15,V6]

4. h) Un ciclo no simple de grado 5.
C= [V1, a4, V6, a11, V3, a13, V5, a14, V6, a4, V1]
i) Árbol generador aplicando el algoritmo constructor.
V2
V1 a3
a5 V3 a10
V5 V4
V6 a19
V7 a12
V8
H1= {1} seleccionamos a5.
H2= {V1, V7} seleccionamos a12.
H3= {V1, V7, V3} seleccionamos a3.
H4= {V1, V7, V3, V2} seleccionamos a10.
H5= {V1, V7, V3, V2, V4} seleccionamos a20.
H6= {V1, V7, V3, V2, V4, V8} seleccionamos a19.
H7= {V1, V7, V3, V2, V4, V8, V5} seleccionamos a12.
H8= {V1, V7, V3, V2, V4, V8, V5, V6} seleccionamos a14.

5. j) Sub-grafo Parcial
V6 V1 V2
a5 V3 a3
a14
a12
V7 V5 V4
a20
a19
V8
k) Demostrar si es eureliano aplicando el algoritmo de Fleury
Se puede concluir, que el grafo no es eureliano, ya que aplicando el algoritmo de
Fleury y partiendo desde cualquier vértice no es posible obtener un ciclo eureliano.
l) Demostrar si es hamiltoniano
Se puede demostrar que si es hamiltoniano, ya que se obtiene una cadena con un ciclo
hamiltoniano:
C=[V1,a1,V2,a3,V3,a11,V6,a14,V5, a16,V4,a20,V8,a18,V7,a5,V1]

6. 2.- Dado el siguiente dígrafo
a) Encontrar matriz de conexión
0 1 1 0 1 0
0 0 1 1 1 0
0 0 0 1 1 0
MC=
1 0 0 0 0 1
0 1 0 1 0 1
0 0 0 0 1 0
b) ¿Es simple? Justifique su respuesta
Si es Simple, debido a que no existen lazos en ningún vértice y tampoco arcos
paralelos.
c) Encontrar una cadena no simple no elemental de grado 5
T= [V1, , V2 ,V3, V4, ,V1, ,V2]
d) Encontrar un ciclo simple
C= [V6, V5, , V4, V6]

7. e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
Se pudo observar que el dígrafo es fuertemente conexo.