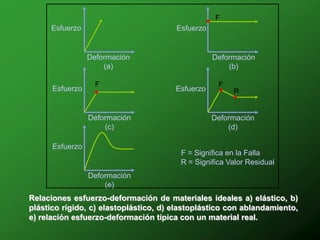
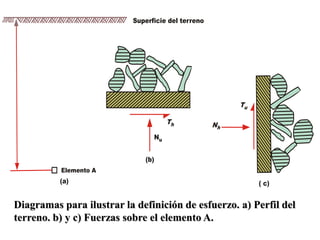
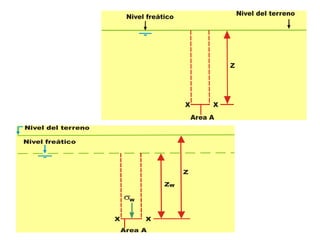
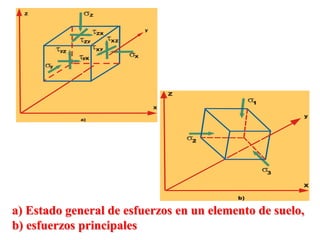
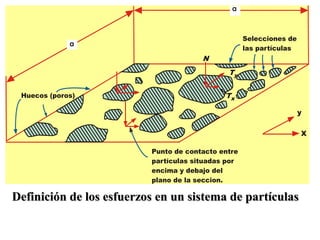
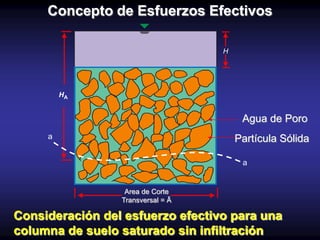
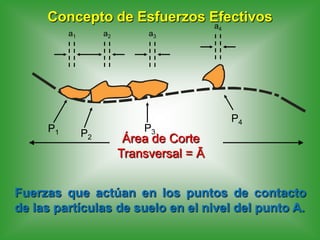
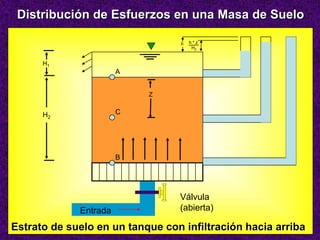
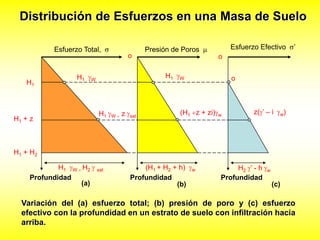
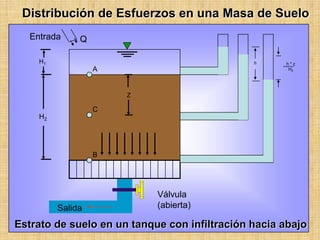
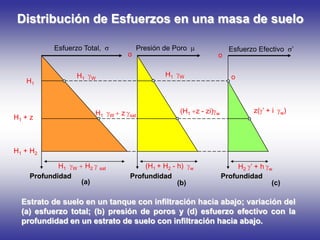
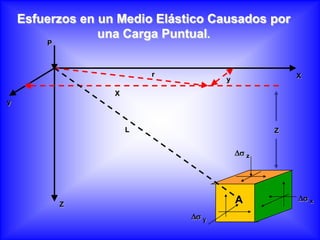
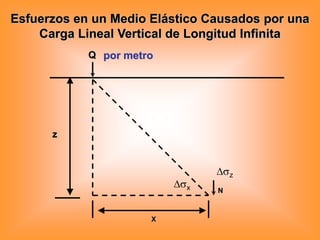
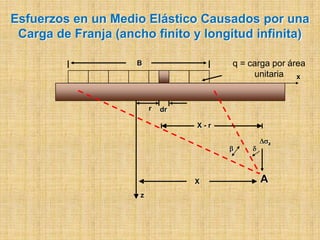
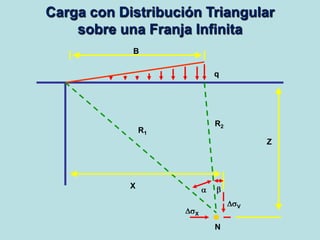
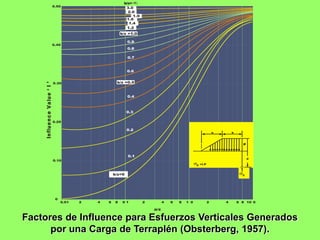
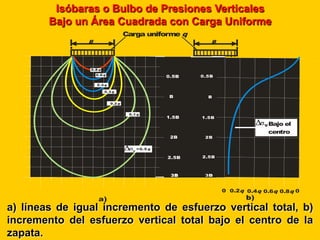
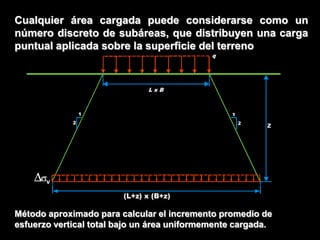
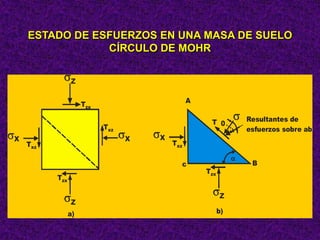
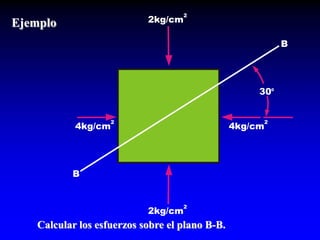
Este documento presenta información sobre esfuerzos geotécnicos. Explica conceptos como esfuerzos efectivos, distribución de esfuerzos en masas de suelo, y esfuerzos causados por cargas puntuales, lineales, de franja y de área. También incluye diagramas y fórmulas para calcular esfuerzos verticales, principales y tangenciales bajo diferentes configuraciones de cargas. Finalmente, muestra factores de influencia y métodos aproximados para calcular incrementos de esfuerzos bajo cargas de áreas circul

1. UNIVERSIDAD NACIONAL MAYOR
DE SAN MARCOS
FACULTAD DE CIENCIAS FISICAS
ESCUELA ACADEMICA DE INGENIERIA
MECANICA DE FUIDOS
ESFUERZOS GEOETÁTICOS
EXPOSITOR: Ing. Flores Talavera A. O.
Lima, c.u. - 2013

2. Problemas de Deformaciones Planas Típicos.
Terraplén
Muro de
Contención
z
z
Y
Y
X
z
X
Y
X
Cimentación Corrida

3. F
Esfuerzo
Esfuerzo
Deformación
(a)
Esfuerzo
F
Deformación
(c)
Esfuerzo
Deformación
(b)
Esfuerzo
F
R
Deformación
(d)
F = Significa en la Falla
R = Significa Valor Residual
Deformación
(e)
Relaciones esfuerzo-deformación de materiales ideales a) elástico, b)
plástico rígido, c) elastoplástico, d) elastoplástico con ablandamiento,
e) relación esfuerzo-deformación típica con un material real.

4. Superficie del terreno
Tu
Th
Nh
Nu
(b)
Elemento A
(a)
( c)
Diagramas para ilustrar la definición de esfuerzo. a) Perfil del
terreno. b) y c) Fuerzas sobre el elemento A.

5. Nivel del terreno
Nivel freático
Z
X
X
Area A
Nivel del terreno
Nivel freático
Z
ZW
W
X
X
Area A

6. Z
Z
y
ZX
XZ
Z
Xy
y
yX
X
y
Z
1
X
y
a)
2
3
X
b)
a) Estado general de esfuerzos en un elemento de suelo,
b) esfuerzos principales

7. a
Selecciones de
las partículas
a
N
Ty
Huecos (poros)
Tx
y
X
Punto de contacto entre
partículas situadas por
encima y debajo del
plano de la seccion.
Definición de los esfuerzos en un sistema de partículas

8. Concepto de Esfuerzos Efectivos
H
HA
Agua de Poro
a
Partícula Sólida
a
Area de Corte
Transversal = Ā
Consideración del esfuerzo efectivo para una
columna de suelo saturado sin infiltración

9. Concepto de Esfuerzos Efectivos
a1
P1
a2
P2
a3
P3
a4
P4
Área de Corte
Transversal = Ā
Fuerzas que actúan en los puntos de contacto
de las partículas de suelo en el nivel del punto A.

10. Distribución de Esfuerzos en una Masa de Suelo
h
h*z
H2
H1
A
Z
C
H2
B
Entrada
Válvula
(abierta)
Estrato de suelo en un tanque con infiltración hacia arriba

11. Distribución de Esfuerzos en una Masa de Suelo
Esfuerzo Total,
H1
H1
H1 + z
o
H1
W
z
sat
’
o
H1
W
Esfuerzo Efectivo
Presión de Poros
o
W
(H1 z + zi)
w
z( ’ – i
w)
H1 + H2
H1 W H2
Profundidad
(a)
sat
(H1 + H2 + h)
Profundidad
(b)
w
H2 ’ - h
Profundidad
w
(c)
Variación del (a) esfuerzo total; (b) presión de poro y (c) esfuerzo
efectivo con la profundidad en un estrato de suelo con infiltración hacia
arriba.

12. Distribución de Esfuerzos en una Masa de Suelo
Entrada
Q
H1
h
A
h*z
H2
Z
C
H2
B
Salida
Válvula
(abierta)
Estrato de suelo en un tanque con infiltración hacia abajo

13. Distribución de Esfuerzos en una masa de suelo
Esfuerzo Total,
H1
H1
o
Presión de Poro
H1
W
H1
H1 + z
o
W
z
sat
Esfuerzo Efectivo
’
o
W
(H1 z - zi)
w
z( ’ + i
w)
H1 + H2
H1 W
Profundidad
H2
(a)
sat
(H1 + H2 - h)
Profundidad
(b)
w
H2 ’ + h
Profundidad
w
(c)
Estrato de suelo en un tanque con infiltración hacia abajo; variación del
(a) esfuerzo total; (b) presión de poros y (d) esfuerzo efectivo con la
profundidad en un estrato de suelo con infiltración hacia abajo.

14. Esfuerzos en un Medio Elástico Causados por
una Carga Puntual.
P
r
X
y
X
y
L
Z
z
A
Z
y
x

15. Esfuerzos causados por un Carga Puntual
Boussinesq (1883) resolvió el problema de los
esfuerzos “producidos en cualquier punto de un
medio homogéneo, elástico e isótropo como
resultado de una carga puntual aplicada sobre la
superficie de un semiespacio infinitamente grande. La
solución de Boussinesq para los esfuerzos normales
en un punto A causado por la carga puntual P es
2
x
2
2
2
P 3x z
x y
y z
(1 2 ) 2
5
2
L
Lr ( L z ) L3r 2

16. Esfuerzos Normales en A causados por
una Carga Puntual
2
y
2
2
2
P 3y z
y x
xz
(1 2 ) 2
5
3 2
2
L
Lr ( L z ) L r
y
z
3Pz 3
5
2 L
donde:
3Pz 3
2
2 5/ 2
2 (r z )
r
x2 y2
L
x2 y 2 z 2
r2 z2
= relación de poisson

17. Esfuerzos en un Medio Elástico Causados por una
Carga Lineal Vertical de Longitud Infinita
Q por metro
z
z
x
X
N

18. Esfuerzos Causados por una Carga
Lineal Vertical de Longitud Infinita
Los incrementos de esfuerzo en N debidos a la
aplicación de una carga lineal Q por metro, son
2Q
z
z
(x
2Q
x
2
2 2
z )
2
x z
2
2 2
(x z )
2Q
xz
3
xz
(x
2
2
2 2
z )

19. Esfuerzos en un Medio Elástico Causados por una
Carga de Franja (ancho finito y longitud infinita)
q = carga por área
unitaria x
B
r
dr
X-r
z
X
z
A

20. Carga Uniformemente Distribuida Sobre
una Franja Infinita
Los incrementos de esfuerzos en el punto A producidos
por una presión uniforme q que actúa sobre un franja
flexible infinitamente larga de ancho B, son los siguientes:
q
z
q
x
q
xz
sen cos(
2 )
sen cos(
2 )
sen sen (
2 )

21. Isóbaras o Bulbo de Presiones Verticales
Bajo una Carga Flexible de Franja
q
B
q
2B
2.5B
= 0.9
0.7
B
0.5
0.06
2B
0.3
0.08
a
Carga de
Franja flexible
a
q
=
0.2
3B
4B
0.1
Planta
0
5B
B
2B

22. Carga con Distribución Triangular
sobre una Franja Infinita
B
q
R2
R1
Z
X
V
X
N

23. Carga con Distribución Triangular
sobre una Franja Infinita
Cuando el esfuerzo aplicado se incrementa linealmente a
través del ancho de la franja, lo cual conduce a una
distribución triangular, los incrementos de esfuerzo en el
punto N están dados por:
q
v
q
x
xz
q
2
x
B
x
B
1
sen 2
2
2
1
2
2
z
R
1n
B
R
1 cos 2
1
sen 2
2
2z
x
B

24. Carga uniformemente distribuida sobre
área circular
una
El incremento del esfuerzo vertical total a una
profundidad z bajo el centro de una área circular
flexible de radio R cargada con una presión uniforme q
esta dado por
v
1
2
1 ( R / z)
q 1
3/ 2
Sin embargo, para puntos diferentes de los situados bajo el
centro de carga, las soluciones tienen una forma extremadamente
complicada (Harr, 1996) y por lo general se presentan en forma
gráfica (Foster y Ahlvin, 1954 ) o en tablas (Ahlvin y Ulery, 1962).
En el punto N , puede escribirse el incremento en el esfuerzo
vertical total como
v
qI

25. Factor influencia l σ
0.001
0
0.004
0.002
0.006 0.01
0.04
0.02
2
0.4
0.8 1
1.5
0
0.5
r
=0.75
R
4
4
0.6
r
=1
R
3
3
5
6
5
7
Carga uniforme q
8
6
7
0.2
2.5
2
R
0.1
0.1
1.25
1
z
E
R
0.06
r
=10
R
R
9
8
V
9
r
V
= q/
10
Valores del factor de influencia /σ para calcular el incremento de esfuerzo
vertical total σv bajo un área circular uniformemente cargada. (Según
Foster y Alhvin, 1954. Reimpresa con la autorización del transportation
Research board).

26. b/z=
3.0
2.0
1.9
1.6
1.4
1.2
0.50
b/z =1.0
0.9
0.40
0.8
0.7
In flu e n c e Va lu e ‘ I ’
0.6
b/z =0.5
0.30
0.4
0.3
0.20
0.2
a
b
P
0.1
Z
0.10
Z =I.P
b/z=0
0
0.01
2
4
6
8
0 1
Z
2
4
6
8
1 0
2
4
6 8 10 0
a/z
Factores de Influence para Esfuerzos Verticales Generados
por una Carga de Terraplén (Obsterberg, 1957).

27. Isóbaras o Bulbo de Presiones Verticales
Bajo un Área Cuadrada con Carga Uniforme
Carga uniforme q
B
B
0.9 q
0.8 q
0 .6 q
0.5B
0.5B
0 .4 q
0 .3 q
B
B
0 .2 q
0 .1 q
1.5B
1.5B
2B
el
centro
2B
2.5B
V
V Bajo
2.5B
= 0.5 q
0 0.2q 0.4q 0.6q 0.8q 0
a)
b)
a) líneas de igual incremento de esfuerzo vertical total, b)
incremento del esfuerzo vertical total bajo el centro de la
zapata.

28. Incremento de Presiones Verticales Bajo
un Área Rectangular con Carga Uniforme
El incremento en el esfuerzo vertical debajo la
esquina de un área
rectangular cargada
uniformemente viene dado por:
v
qI
Donde I es función de m y n, parámetros
definidos como:
m
n
B
z
L
z

29. Presion uniforme q
0.25
0.24
B
0.23
m=3.0
m=2.4
m=2.
m=1.8
m=
m = 1 .6
m = 1 .4
0.22
L
Z
V
N
=ql
Nota: m y n son intercambiables
V
0.18
m=1.2
0.21
m=1.0
0.20
m=0.9
0.19
0.18
m=0.8
m=0.7
0.17
m=0.6
Factor de influencia I
0.16
0.15
0.14
m=0.5
0.13
m=0.4
0.12
0.11
0.10
m=0.3
0.09
0.08
0.07
m=0.2
0.06
0.05
0.04
m=0.1
0.03
0.02
0.01
0.00
0.01 0.02 0.04 0.06
m=0.0
0.1
0.2 0.3 0.4 0.6 0.8 1
n
2
3 456
8
10
Valores del factor de influencia I para calcular el incremento de esfuerzo
vertical total
v bajo la esquina de una área rectangular uniformemente
cargada (Según Fadum, 1948)

30. Cálculo aproximado del incremento de
esfuerzo vertical
Para áreas circulares o rectangulares uniformemente
cargadas, puede hacerse un cálculo aproximado del
incremento de esfuerzo vertical total suponiendo que la
carga aplicada se distribuye dentro de un cono truncado
o una pirámide truncada formados por lados con
pendiente de 2 en la vertical y 1 en la Horizontal, por
ejemplo, si el área cargada es un rectángulo de longitud L
y ancho B, el incremento promedio en el esfuerzo vertical
total a una profundidad z estará dado aproximadamente
por
v
(L
qLB
z )( B
z)

31. Cualquier área cargada puede considerarse como un
número discreto de subáreas, que distribuyen una carga
puntual aplicada sobre la superficie del terreno
q
LxB
1
1
2
2
Z
(L+z) x (B+z)
Método aproximado para calcular el incremento promedio de
esfuerzo vertical total bajo un área uniformemente cargada.

32. Carga puntual
Expresión de Boussinesq
3P
v
3
2 z
P 2 x 2 x 200 800k
Z(m)
V
(KN/M2)
0,25
0,50
1,00 1,50
2,00 2,50 3,00 3,50 4,00
6.111,5 1.527,9 382,0 169,3 95,5 61,1 42,4 31,2 23,9

33. ESTADO DE ESFUERZOS EN UNA MASA DE SUELO
CÍRCULO DE MOHR
Z
A
Tzx
T 0
Txz
X
X
Txz
X
Txz
c
Tzx
Z
a)
Resultantes de
esfuerzos sobre ab
B
Tzx
Z
b)

34. 3
T
Dirección de
REPRESENTACIÓN
DE ESFUERZOS
MEDIANTE EL
CÍRCULO DE MOHR
A
1
C
B
3
Dirección de
(a)
T
A ( Coordenados
1
-
1
,T )
a) estado de esfuerzos en
un punto.
3
2
2
Circulo de Mohr
1
+
2
3
(b)
b) Diagrama de Mohr para
el estado de esfuerzos
en un punto.

35. Representación de los esfuerzos mediante el
círculo de Mohr.
cos2
1
(
1
sen 2
3
3 ) sen cos
1
3
1
2
1
2
3
2
3
cos 2
sen 2
El esfuerzo tangencial máximo en un punto, max es
siempre igual a ( 1- 3)/2; es decir, el esfuerzo tangencial
máximo equivale al radio del círculo de Mohr. Este esfuerzo
tangencial máximo se produce en planos que forman 45
con la dirección del esfuerzo principal mayor.

36. 2kg/cm
Ejemplo
2
B
300
4kg/cm
2
4kg/cm
B
2kg/cm
2
Calcular los esfuerzos sobre el plano B-B.
2

37. 1.
2.
3.
4.
5.
6.
Se representa los puntos (4,0) y (2,0).
Se dibuja el círculo, utilizando estos puntos para definir el diámetro.
Se traza la línea AA’ por el punto (2,0), paralela al plano sobre el cual
actúa el esfuerzo (2,0).
La intersección de A’A’ con el círculo Mohr en el punto (4,0) es el polo.
Se traza la línea B’B’ por Op, paralela a BB.
Se leen las coordenadas del punto X donde B’B’ corta al círculo de
Mohr.
C´
1
Op
Op
B´
B’
A´
A’
A´
0
X
-1
1
2
2
B´
B’
3
3
C´
4

38. Sobre BB
= 2.5 kg/cm2
= -0.87 kg/cm2
2.5 kg/cm
2
Respuesta
4 kg/cm
2
0.87
2 kg/cm2

39. Otra solución. Los pasos 1 y 2 igual que antes.
3. Traza´por el punto (4.0) la línea C’C’ paralela al plano sobre
el que actúa el esfuerzo (4.0). C’C’ es vertical.
4. C’C’ corta al círculo de Mohr solamente en (4.0) de forma
que este punto es el polo Op. Los pasos 5 y 6 análogos al caso
anterior.
Solución por medio de las ecuaciones
1
4kg / cm 2
3
2kg / cm 2
120
4 2 4 2
cos 240 3 cos60 2.5kg / cm2
2
2
4 2
sen 240
sen60
0.866kg / cm2
2
(preguntas para el alumno. ¿Por qué es
habria sido diferente si = 300 ?)
=120 ? ¿El resultado

40. DIAGRAMAS p-q
En muchos problemas conviene representar, sobre un
diagrama único, muchos estados de esfuerzos para una
determinada muestra del suelo. En otros problemas se
representa en un diagrama de este tipo el estado de
esfuerzos de muchas muestras diferentes. En tales casos
resulta muy pesado trazar los círculos de Mohr, e
incluso mas difícil ver lo que se ha representado en el
diagrama después de dibujar todos los círculos .
Otro método para dibujar el estado de esfuerzos puede
ser adoptar un punto representativo de los esfuerzos
cuyas coordenadas son

41. p
q
1
3
2
1
+ si 1 forma un ángulo igual o
menor de 45 con la vertical
3
2
- si 1 forma un ángulo menor de
45 con la horizontal
En la mayoría de los casos en los que se utiliza la
representación puntual, los esfuerzos principales actúan
sobre planos verticales y horizontales. En este caso, la
ecuación se reduce a
p
h
2
,q
h
2

42. Este método equivale a representar un punto único de
un circulo de Mohr: el punto mas alto si q es positivo o
el mas bajo si q es negativo. Numéricamente, q equivale
a la mitad del esfuerzo desviador.
Conociendo los valores de p y q para un cierto estado de
esfuerzos, se posee toda la información necesaria para
dibujar el círculo de Mohr correspondiente. Sin
embargo, el empleo de un diagrama p-q no exime de
utilizar el círculo de Mohr para determinar la magnitud
de los esfuerzos principales a partir de un determinado
estado de esfuerzos.

43. FIN