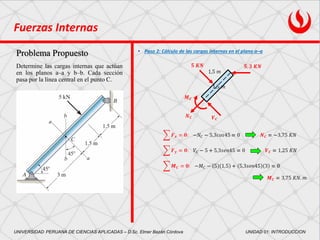
El documento presenta varios problemas de ingeniería estructural que involucran el cálculo de fuerzas internas y esfuerzos. El primer problema implica determinar las cargas internas en dos puntos de una viga. El segundo problema busca determinar las cargas internas en dos secciones de una viga. Finalmente, el tercer problema trata sobre calcular la deformación unitaria normal de un cable sometido a una fuerza.

1. 1
Problema Propuesto
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas
Determine las cargas internas en los puntos D y E. El
punto E está localizado justo a la derecha de la carga
de 3 Kip.
• Paso 1: Cálculo de las reacciones en los apoyos

2. 2
Problema Propuesto
Determine las cargas internas en los puntos D y E. El
punto E está localizado justo a la derecha de la carga
de 3 Kip.
• Paso 1: Cálculo de las reacciones en los apoyos
• Paso 2: Cálculo de las cargas internas en el punto D
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas

3. 3
Problema Propuesto
Determine las cargas internas en los puntos D y E. El
punto E está localizado justo a la derecha de la carga
de 3 Kip.
• Paso 2: Cálculo de las cargas internas en el punto E
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas

4. 4
Problema Propuesto
Determine las cargas internas que actúan
en los planos a–a y b–b. Cada sección
pasa por la línea central en el punto C.
• Paso 1: Cálculo de las reacciones en los apoyos
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas

5. 5
• Paso 2: Cálculo de las cargas internas en el plano a–a
Problema Propuesto
Determine las cargas internas que actúan
en los planos a–a y b–b. Cada sección
pasa por la línea central en el punto C.
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas

6. 6
Problema Propuesto
Determine las cargas internas que actúan en los
planos a–a y b–b. Cada sección pasa por la línea
central en el punto C.
• Paso 2: Cálculo de las cargas internas en el plano b–b
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas

7. 𝑽𝒙 𝑽𝒚
𝑵
𝑴𝒙 𝑴𝒚
𝑻
𝑨
𝒙
𝒚
𝒛
• Para un estado tridimensional de esfuerzos, tenemos las siguientes cargas
internas: una fuerza normal (N), dos fuerzas cortantes (Vx y Vy), un
momento de torsión (T) y dos momentos flectores.
• La representación de los esfuerzos en un punto se realiza a través de un
elemento infinitesimal del cuerpo, donde la cara superior del cubo (color
amarillo) es la única cara visible después de realizar el corte respectivo y las
demás caras no son visibles ya que están incluidas en el interior del cuerpo.
Si suponemos un estado uniaxial de esfuerzos, tenemos la siguiente
representación de los esfuerzos en un punto:
• Recordar que los esfuerzos normales son los mismos en cualquiera de los
puntos de la sección transversal, eso se debe a que consideramos una
deformación uniforme en el cuerpo y, por tanto, el esfuerzo corresponderá
a un esfuerzo normal promedio. De igual manera, consideramos también
un esfuerzo cortante promedio en la sección transversal de análisis.
𝝈
𝝈
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Fuerzas Internas y Esfuerzos

8. 8
Problema Propuesto
perm 29ksi
 
perm 10ksi
 
Determine el espesor requerido del
miembro BC y el diámetro de los pines A
y B si el esfuerzo permisible normal de
BC es y el cortante permisible
• Paso 1: Cálculo de las reacciones en los apoyos
• Paso 2: Cálculo de las cargas internas del elemento BC y de los pasadores
El elemento BC trabaja en tracción (fuerza normal) y los pasadores
trabajan en cortante (fuerza cortante). El pasador B trabaja a cortante
doble y el pasador A a cortante simple.
La fuerza resultante en A es:
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Esfuerzo Permisible y Diseño

9. 9
Problema Propuesto
perm 29ksi
 
perm 10ksi
 
Determine el espesor requerido del
miembro BC y el diámetro de los pines A
y B si el esfuerzo permisible normal de
BC es y el cortante permisible
• Paso 3: Cálculo de los esfuerzos en el elemento BC y en los pasadores
• Paso 4: Cálculo del espesor del elemento BC y el diámetro de los pasadores
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Esfuerzo Permisible y Diseño

10. 10
Problema Propuesto
La fuerza aplicada a la palanca de brazo
rígido causa un giro horario de 3°
alrededor del pasador A. Determine la
deformación normal unitaria
desarrollada en el cable. Originalmente,
el cable se encuentra sin deformar.
• Paso 1: Cálculo de la longitud final del cable
𝐿0
𝐿𝑓
0,6𝑠𝑒𝑛45
0,6𝑐𝑜𝑠45
93°
Para determinar la deformación unitaria debemos trabajar con figuras
geométricas, en particular, triángulos, que nos permitan obtener las
dimensiones finales requeridas para dicho cálculo, utilizando la ley de
senos o cosenos.
𝐿𝑓 = (0,6𝑐𝑜𝑠45)2+(0,6𝑠𝑒𝑛45)2−(2)(0,6𝑐𝑜𝑠45)(0,6𝑠𝑒𝑛45)(𝑐𝑜𝑠93)
𝑳𝒇 = 0,616 𝑚
• Paso 2: Cálculo de la deformación unitaria normal
𝜀 =
𝐿𝑓 − 𝐿0
𝐿0
=
0,616 − 0,6
0,6
𝜺 = 𝟎, 𝟎𝟐𝟕 𝒎/𝒎
UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS – D.Sc. Elmer Bazán Córdova UNIDAD 01: INTRODUCCION
Deformación Unitaria