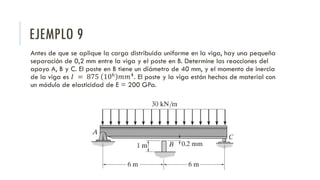
Este documento trata sobre la deflexión en vigas. Explica conceptos como la curva elástica, la relación entre momento y radio de curvatura, y métodos para determinar la curva elástica como la integración directa, el método de momento de área y la superposición. También cubre vigas estáticamente indeterminadas y proporciona varios ejemplos numéricos para ilustrar los diferentes métodos.

1. DEFLEXIÓN EN VIGAS Jhon Fernando Pazos O.

2. INTRODUCCIÓN
La deflexión de una viga o eje a menudo
debe limitarse para proporcionar la
integridad y estabilidad de una estructura o
máquina, y prevenir el agrietamiento de
cualquier material quebradizo adherido
como concreto o vidrio. Además, los códigos
restricciones a menudo requieren que estos
miembros no vibren.

3. CURVA ELÁSTICA
Los apoyos generan restricción del
desplazamiento.
Los empotramientos también generan
restricción de desplazamiento y
adicionalmente hacen que la curva
tenga pendiente cero.
En el lugar del máximo
desplazamiento entre dos apoyos la
pendiente es cero
Donde el momento es positivo la
curva elástica tiene concavidad
positiva y viceversa.

4. RELACIÓN MOMENTO RADIO DE CURVATURA

5. PENDIENTE Y DESPLAZAMIENTO POR
INTEGRACIÓN

6. CONDICIONES DE BORDE

7. EJEMPLO
Para la viga mostrada calcula la curva elástica

8. EJEMPLO 2
Determine la pendiente y la deflexión del extremo A de la viga en voladizo. E = 200 GPa e I =
65,0 (10^6) mm4.

9. EJEMPLO 3
Determinar la deflexión máxima de la viga simplemente apoyada. La viga está
hecha de madera con un módulo de elasticidad de E = 1,5 (10^3) ksi y una sección
transversal rectangular de ancho b = 3 in. y altura h = 6 in.

10. EJEMPLO 3
Determinar la deflexión máxima del piso del avión. Asuma que el fuselaje solo
genera reacciones en la dirección vertical. Asuma EI constante.

11. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DE FUNCIONES DISCONTINUAS
Funciones de Macaulay

12. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DE FUNCIONES DISCONTINUAS
Funciones de singularidad

13. EJEMPLO FUNCIÓN DISCONTINUA

14. EJEMPLO 4
El eje soporta las dos cargas de polea mostradas. Determinar la ecuación de la
curva elástica. Los rodamientos en A y B sólo ejercen reacciones verticales sobre el
eje. EI es constante

15. EJEMPLO 5
La viga soporta las dos cargas mostradas. Determinar la ecuación de la curva
elástica. EI es constante

16. EJEMPLO 6
La viga soporta las dos cargas mostradas. Determinar la ecuación de la curva
elástica. EI es constante

17. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DEL MÉTODO DE MOMENTO DE ÁREA
Primer teorema de momento

18. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DEL MÉTODO DE MOMENTO DE ÁREA
Segundo teorema de momento

19. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DEL MÉTODO DE MOMENTO DE ÁREA
Segundo teorema de momento

20. EJEMPLO 7
La viga soporta las dos cargas mostradas. Determinar la pendiente en A y la
máxima deflexión en la viga. EI es constante

21. DETERMINACIÓN DE LA CURVA ELÁSTICA POR
MEDIO DEL MÉTODO DE SUPERPOSICIÓN
= +

24. EJEMPLO 7
La viga soporta las dos cargas mostradas. Determinar la pendiente en A y la
máxima deflexión en la viga por medio del método de superposición . EI es
constante.

25. VIGAS ESTÁTICAMENTE INDETERMINADAS
Se dice que una viga es estáticamente
indeterminada cuando las reacciones
desconocidas superan las ecuaciones de
equilibrio.
Las reacciones redundantes son aquellas
que no son necesarias para el equilibrio
Se pueden resolver por los métodos usados
anteriormente:
Integración directa
Momento de área
Superposición

26. VIGAS ESTÁTICAMENTE INDETERMINADAS:
MÉTODO DE INTEGRACIÓN DIRECTA
La viga soporta las dos cargas mostradas. Determinar las reacciones en A, B y C.
Luego dibuje los diagramas de cortante y momento. EI es constante.

27. VIGAS ESTÁTICAMENTE INDETERMINADAS:
MÉTODO DE SUPERPOSICIÓN
La viga se considera inicialmente sin las reacciones
redundantes y se halla su deflexión o pendiente.
Luego se considera la reacción sin las cargas
externas y se calcula su deflexión o pendiente .
Se establece una ecuación de continuidad la cual
varia en función del problema

28. VIGAS ESTÁTICAMENTE INDETERMINADAS:
MÉTODO DE SUPERPOSICIÓN
Ecuación de Compatibilidad
Ecuaciones de Compatibilidad

29. EJEMPLO 8
Determine la deflexión en el extremo B de la barra empotrada de acero A-36. El
resorte tiene una rigidez de k = 2 N/mm. La barra tiene una sección rectangular
cuadrada de 5mm de ancho y 10 mm de alto. También, dibuje los diagramas de
momento y cortante para la barra

30. EJEMPLO 9
Antes de que se aplique la carga distribuida uniforme en la viga, hay una pequeña
separación de 0,2 mm entre la viga y el poste en B. Determine las reacciones del
apoyo A, B y C. El poste en B tiene un diámetro de 40 mm, y el momento de inercia
de la viga es 𝐼 = 875 106
𝑚𝑚4
. El poste y la viga están hechos de material con
un módulo de elasticidad de E = 200 GPa.

31. EXTRA
La viga soporta las dos cargas mostradas. Determinar la deflexión en el punto c de
la viga. EI es constante.

32. VIGAS ESTÁTICAMENTE INDETERMINADAS:
MÉTODO DE MOMENTO DE ÁREA
Similar al método de superposición lo ideal
es descomponer la viga en cada una de sus
cargas externas aplicadas y reacciones
redundantes y realizar un diagrama de
M/EI, para cada una de ellas.
Luego empleando alguno de los dos
teoremas visto resolver el problema
despejando la reacción desconocida.

33. EJEMPLO 10
La viga soporta las dos cargas mostradas. Determinar las reacciones en A y B. Luego
dibuje los diagramas de cortante y momento. EI es constante.