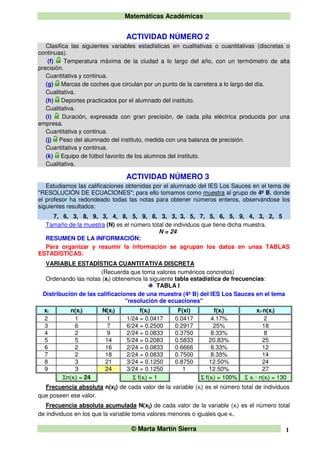
El documento presenta información estadística sobre las calificaciones obtenidas por estudiantes en un tema. Incluye una tabla con las calificaciones de un grupo, clasificadas como variables cuantitativas discretas. La tabla muestra las frecuencias absolutas, relativas y acumuladas de cada calificación, así como el tamaño total de la muestra.

1. Matemáticas Académicas
© Marta Martín Sierra 1
ACTIVIDAD NÚMERO 2
Clasifica las siguientes variables estadísticas en cualitativas o cuantitativas (discretas o
continuas).
(f) Temperatura máxima de la ciudad a lo largo del año, con un termómetro de alta
precisión.
Cuantitativa y continua.
(g) Marcas de coches que circulan por un punto de la carretera a lo largo del día.
Cualitativa.
(h) Deportes practicados por el alumnado del instituto.
Cualitativa.
(i) Duración, expresada con gran precisión, de cada pila eléctrica producida por una
empresa.
Cuantitativa y continua.
(j) Peso del alumnado del instituto, medida con una balanza de precisión.
Cuantitativa y continua.
(k) Equipo de fútbol favorito de los alumnos del instituto.
Cualitativa.
ACTIVIDAD NÚMERO 3
Estudiamos las calificaciones obtenidas por el alumnado del IES Los Sauces en el tema de
"RESOLUCIÓN DE ECUACIONES"; para ello tomamos como muestra al grupo de 4º B, donde
el profesor ha redondeado todas las notas para obtener números enteros, observándose los
siguientes resultados:
7, 6, 3, 8, 9, 3, 4, 8, 5, 9, 8, 3, 3, 3, 5, 7, 5, 6, 5, 9, 4, 3, 2, 5
Tamaño de la muestra (N) es el número total de individuos que tiene dicha muestra.
N = 24
RESUMEN DE LA INFORMACIÓN:
Para organizar y resumir la información se agrupan los datos en unas TABLAS
ESTADÍSTICAS:
VARIABLE ESTADÍSTICA CUANTITATIVA DISCRETA
(Recuerda que toma valores numéricos concretos)
Ordenando las notas (xi) obtenemos la siguiente tabla estadística de frecuencias:
TABLA I
Distribución de las calificaciones de una muestra (4º B) del IES Los Sauces en el tema
"resolución de ecuaciones"
xi n(xi) N(xi) f(xi) F(xi) f(xi) xi·n(xi)
2 1 1 1/24 = 0.0417 0.0417 4.17% 2
3 6 7 6/24 = 0.2500 0.2917 25% 18
4 2 9 2/24 = 0.0833 0.3750 8.33% 8
5 5 14 5/24 = 0.2083 0.5833 20.83% 25
6 2 16 2/24 = 0.0833 0.6666 8.33% 12
7 2 18 2/24 = 0.0833 0.7500 8.33% 14
8 3 21 3/24 = 0.1250 0.8750 12.50% 24
9 3 24 3/24 = 0.1250 1 12.50% 27
Σn(xi) = 24 Σ f(xi) = 1 Σ f(xi) = 100% Σ xi · n(xi) = 130
Frecuencia absoluta n(xi) de cada valor de la variable (xi) es el número total de individuos
que poseen ese valor.
Frecuencia absoluta acumulada N(xi) de cada valor de la variable (xi) es el número total
de individuos en los que la variable toma valores menores o iguales que xi.

2. 2
Frecuencia relativa f(xi) de cada valor de la variable (xi) es el cociente que resulta de dividir
su frecuencia absoluta por el número total de individuos. Nos indica el número de veces que
aparece cada suceso con respecto al número total de observaciones. Es el tanto por uno de la
variable, de modo que si lo multiplicamos por 100, obtendremos el porcentaje con el que
aparece cada valor de la variable en la muestra.
Frecuencia relativa acumulada F(xi) de cada valor de la variable (xi) es el cociente que
resulta de dividir la frecuencia absoluta acumulada por el número total de individuos.
CUESTIONES DIRECTAS
A la vista de la tabla anterior, contesta directamente a las siguientes cuestiones, señalando
el lugar de la tabla y el símbolo matemático correspondiente.
(a) ¿Qué indica que xi = 7 y n(xi) = 2?
Hay 2 alumnos que han obtenido un 7
(b) ¿Cuántas personas obtuvieron un 9?
n(xi) = 3
(c) ¿Cuántas personas obtuvieron un 7 o menos?
N(xi) = 18
(d) ¿Cuántas personas suspendieron?
N(xi) = 9
(e) ¿Qué significa que xi es 5 y f(xi) es 0’2083?
0’2083 lo pasaríamos a porcentaje…
Hay un 20.83% de los alumnos que han obtenido una calificación de 5.
(f) ¿Dónde se expresa, en la tabla, el número total de observaciones que realizamos?
Lo podemos encontrar en varios lugares, por ejemplo:
- En el valor que tiene la expresión Σn(xi)
- En la última celda de la columna N(xi)
(g) ¿Qué quiere decir si la frecuencia relativa acumulada de un dato me da 3?
- Que hemos realizado mal las operaciones pues el valor máximo que puede tener una
frecuencia relativa acumulada es 1.
(h) Justifica qué es más informativa según tu criterio, la frecuencia relativa o la absoluta.
La frecuencia absoluta nos da el número de individuos que toma cada
valor de la variable sobre el total, mientras que la frecuencia relativa nos da
el tanto por uno, que al multiplicarlo por cien nos da porcentaje. Por esto la
frecuencia relativa es más informativa que la absoluta, nos da una mayor
información directa.
(i) ¿Cuál es el máximo valor que puede tomar una frecuencia relativa?
Ya hemos visto que la frecuencia relativa no puede pasar de 1, ya que en el numerador
no puede haber más individuos que en el denominador, donde aparece el número total de los
mismos.