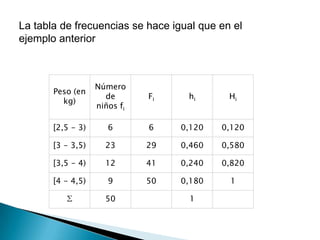
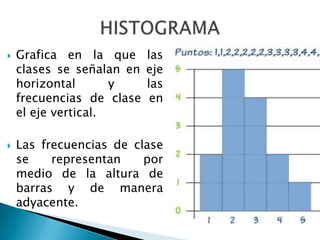
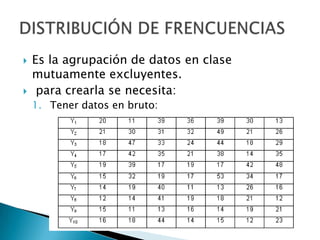
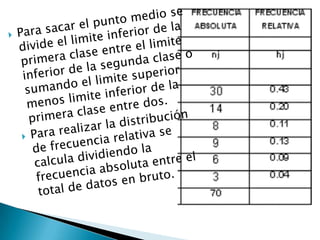
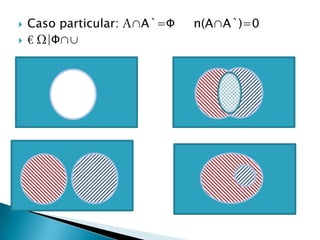
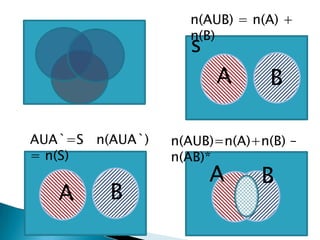
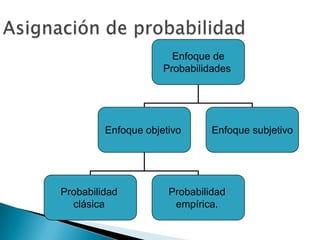
Este documento habla sobre estadística y sus aplicaciones. La estadística se divide en descriptiva e inferencial. La descriptiva organiza y resume datos de forma informativa usando tablas de frecuencia, histograma y polígonos de frecuencia. La inferencial deduce propiedades de poblaciones a partir de muestras. Se describen también conceptos como media, mediana, varianza, desviación estándar y teoría de conjuntos.

1. ESTADISTICA

2. CONSTRUCCIÓN DE FRECUENCIA

3. POLIGONO DE FRECUENCIA E HISTOGRAMA

4. MEDIA DE DATOS AGRUPADOS

5. DESVIACIÓN MEDIA

6. APLICACIONES

7. CONJUNTOS

8. PROBABILIDADESTADÍSTICAS

9. ESTADISTICAHABLAR DE ESTADISTICA ES HABLAR DE DATOS UN FENOMENO

10. ACONTECIMIENTO

11. SITUACIONNOS AYUDAN DE CIERTA FORMA A CONOCER O A ENTENDER Y RECONOCER DIVERSAS SITUACIONES, EN LA VIDA.SI SOMOS FABRICANTES, MAQUILADORES, COCINEROS, PODEMOS OBSERVAR LA FRECUENCIA DE ERRORES EN NUESTRO TRABAJO, LA EFICIENCIA DE NUESTRO NEGOCIO, EL PROMEDIO DE PRODUCTOS FABRICADOS POR DIA, TANTOS FENOMENOS-HECHOS OCURRIDOS EN NUESTRO TRABAJO, LOS PODEMOS VISUALIZAR DE MANERA REREPRESENTATIVA GRACIAS A LA ESTADISTICA.

12. Es la ciencia que recoge, organiza, presenta, analiza e interpreta datos con el fin de proporcionar la toma de decisiones mas eficaz.el estudio de la estadística se divide en dos categorías: la estadística descriptiva y la estadística inferencial.Estadística

13. Método para organizar, resumir y presentar datos de manera informativa (datos concretos).Ejemplos de estadística descriptiva pueden ser: Los datos del censo de población.La cantidad de robos ocurridos en el ultimo mes en una comunidad.La cantidad de pacientes atendidos en un hospital en el ultimo año.Estadística descriptiva

14. Métodos empleados para determinar una propiedad de una población con base en la información de una muestra (sirve para pronosticar).Población: conjunto de individuos u objetos de interés o medias obtenidas a partir de todos los individuos u objetos de interés.Muestra: porción o parte de la población de interés .Estadística inferencial ó Inferencia estadística

15. Ejemplo: una encuesta reciente mostró que solamente el 15% de los estudiantes de secundaria podía resolver problemas que incluyeran fracciones.Ejemplo: una empresa de publicidad solicito a una muestra de 196 consumidores, que probaran un platillo a base de verdura. De las 196 personas de la muestra 117 dijeron que comprarían el alimento si se comercializaba.

16. Cuando la estadística que se estudia es de naturaleza no numérica, recibe el nombre de variable cualitativa o atributo. Ejemplo: filiación religiosa, tipo de automóvil que posee, estado de nacimiento, color de ojos, género.cuando la variable que se estudia aparece en una forma numérica, la variable se denomina variable cuantitativa.Las variables cuantitativas pueden ser discretas o continuas.Tipos de variables

17. El nivel de medición de los datos rige los cálculos que se llevan a cabo con el fin de resumir y presentar los datos. Existen cuatro niveles de medición: nominal, ordinal, de intervalo y de razón.La escala de medida nominal, puede considerarse la escala de nivel más bajo. Se trata de agrupar objetos en clases.Niveles de medición

18. La escala ordinal, por su parte, recurre a la propiedad de orden de los números.La escala de intervalos iguales está caracterizada por una unidad de medida común y constante. Es importante destacar que el punto cero en las escalas de intervalos iguales es arbitrario, y no refleja en ningún momento ausencia de la magnitud que estamos midiendo. La escala de coeficientes o Razones es el nivel de medida más elevado y se diferencia de las escalas de intervalos iguales únicamente por poseer un punto cero propio como origen.A iguales diferencias entre los números asignados corresponden iguales diferencias en el grado de atributo presente en el objeto de estudio.

19. El primer procedimiento a estudiar para organizar y resumir un conjunto de datos es una tabla de frecuencias. Tabla de frecuencias: agrupación de datos cualitativos en clases mutuamente excluyentes que muestran el número de observaciones en clase.Descripción de datos

20. Ejemplo: Se ha controlado el peso de 50 recién nacidos, obteniéndose los siguientes resultados:

21. La tabla de frecuencias se hace igual que en el ejemplo anterior

22. Para representar el histograma, marcamos los intervalos en el eje x, en este caso los intervalos del peso de los niños el nacer.Dibujamos rectángulos de base los intervalos del peso y de altura el número de niños fi que forman parte de ese intervalo.Por ser una distribución continua obtenemos áreas de cada intervalo, no hay separación entre los intervalos.

24. POLIGONO DE FRECUENCIASMuestra la forma que tiene una distribución.Consiste en segmentos de recta que conectan los puntos formados por intersecciones.

25. Grafica en la que las clases se señalan en eje horizontal y las frecuencias de clase en el eje vertical.Las frecuencias de clase se representan por medio de la altura de barras y de manera adyacente. HISTOGRAMA

26. Es la agrupación de datos en clase mutuamente excluyentes. para crearla se necesita:Tener datos en bruto:DISTRIBUCIÓN DE FRENCUENCIAS

27. Definir el numero de clases:Con la formula: Donde K es: total de datos igualar a 2kPor lo tanto seria:K=(log70)/(log2)= 6.12 =6!!!!!Determinar el intervalo de clases:i>H-L/K donde:H=EL MAXIMO VALOR L: MINIMO VALORi=53-11/6= >>7Por lo tanto para indicar la distancia se le suma el dato menor al resultado :11+7= 18

28. Edades y numero de estudiantes (frecuencia absoluta):

29. Para sacar el punto medio se divide el limite inferior de la primera clase entre el limite inferior de la segunda clase o sumando el limite superior menos limite inferior de la primera clase entre dos. Para realizar la distribución de frecuencia relativa se calcula dividiendo la frecuencia absoluta entre el total de datos en bruto.

30. La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.MEDIA GEOMETRICA

31. MEDIA DE DATOS NO AGRUPADOSLa suma de las desviaciones de todas las puntuaciones de una distribución respecto a la media de la misma igual a cero.8 − 7.6 + 3 − 7.6 + 5 − 7.6 + 12 − 7.6 + 10 − 7.6 == 0. 4 − 4.6 − 2.6 + 4. 4 + 2. 4 = 0

33. Es el promedio de los dos elementos de en medio.Ordenar del menor al mayor y tomar el valor que queda en medio. 4.2, 4.3,4.7,4.8,5.0,5.1,9.0=7+1/2=4 o bien 4.8 MEDIANA

34. RANGOREPRESENTA LA DIFERENCIA ENTRE LOS VALORES MAS GRANDES Y MENORES DE UN CONJUNTO DE DATOS.863, 903, 957, 1041 1138, 1204, 1354, RANGO: 1354 – 863 = 491 su utilidad como medida de dispersión

35. Cuartiles, Deciles y percentilesLos cuartiles se dividen a un conjunto de observaciones en cuatro partes iguales Q1 representa el 25 % Q2 el 50% y Q3 el 75% de las observaciones.Los Deciles dividen un conjunto de observaciones en 10 partes iguales.(100/10)Los percentiles en 100 partes iguales.(100/n)Lp representa la ubicación del cierto percentil que se busca. Lp= (n+1) p/ 100.

36. Ejemplo: 0.10, 0.12, 0.23, .32, .45, .48, .50, .51, .53, .58, .59, .66, 0.67, .69, .77, .83, .89, .95, 1.10, 1.20.Mediana= 20Rango= 1.20-0.10= 1.10L25= 20+1(25/100)= 5.25 dif: .45 y .48=.03 (.03)(.25)= .0075L25= .45+.0075=.4575

37. ejemplo24, 28, 32, 32, 38, 40, 42, 44, 46, 54.14, 10, 6, 6 , 0, 2 , 4 , 6 , 8 , 16.Calcular rango: 54-24= 30Calcular la media: 380/10= 38Desviación media: 14+10+6+6+0+2+4+6+8+16= 72/10=7.2

38. Varianza y desviación estándarVarianza de la población=Elemento u observaciòn = XMedia de la población= Número total de elementos de la población= NSuma de los valores(x-m)2 o todos los valores de X 2=

39. ejemploA) Calcule la varianza de la muestraB) determine la desviación estándar78, 80, 87, 88, 97, 101, 101, 103, 106, 110.La suma 951 /10 = 95.195.1-78= 17.1 x2= 29295.1-80=15.1x2= 228.0195.1-87= 8.1x2= 65.6195.1-88=7.1x2= 50.4195.1-97= 1.9x2= 3.6195.1-101= -5.9x2= 34.8195.1-101= -5.9x2= 34.8195.1-103= -7.9x2= 62.4195.1-106= -10.9x2= 118.8195.1-110= -14.9x2= 222.01 + 1112.49 123.61 varianza 11.11 desviación estándar

40. Regla empiricaDe una muestra del pago de energía eléctrica semejante a una distribución simétrica en forma de campana se han obtenido los siguientes datos una madia de la muestra de 500$ y con una desviación de 20$ de acuerdo con la regla empírica indique.A) entre que dos cantidades se encuentra aprox. El 68% de los pagos mensuales de energía.B) entre que dos se encuentran cerca del 95% de los pagos mensuales.C) entre que dos cantidades se encuentran todos los pagos mensuales de energía eléctrica.A) B) C)

41. Teoría de ConjuntosDefinición: Informal de conjunto: un conjunto es una colección bien determinada de elementos.Si un objeto pertenece al conjunto considerado, se dice que es un elemento de eses conjunto.Las letras mayúsculas A,B,C,…, se utilizan generalmente para denotar los conjuntos y las letras minúsculas para denotar elementos de dichos conjuntos.

42. Existen dos métodos usuales para determinar un conjunto:1.- Por enumeración o extensión: se enumeraran todos los elementos de un conjunto y se encierran entre corchetes o llaves.A= {x.y.z} Significa que el conjunto A tiene los elementos x,y,z.

43. Métodos usuales para determinación:2.- Por descripción o compresión: se define al conjunto por la frase descriptiva encerrada entre corchetes, conviniendo en que solo los objetos que satisfacen la descripción son elementos del conjunto.E= {x|x es una vocal}

44. CONJUNTO UNIVERSALEs un conjunto de referencia.Se representa por S, Ω ò U.CONJUNTO VACIO:No posee ningún elemento y se simboliza por Φ (Φse lee: “el conjunto vacío”).

45. CONJUNTO FINITOEs aquel cuyos elementos se pueden listar exhaustivamente, y contar uno por uno hasta el ultimo.CONJUNTO INFINITOEs aquel cuyos elementos no se pueden listar exhaustivamente porque nunca llega el ultimo.

46. DIAGRAMA DE VENNUn conjunto se puede representar por un área delimitada por una línea cerrada, generalmente se utilizan los círculos y los óvalos.Se acostumbra representar un conjunto universal mediante un rectángulo.

47. El complemento de todo conjunto A, con respecto a un determinado conjunto de referencia, es el conjunto de los elementos de dicho conjunto universal que no pertenecen a A.

48. EJEMPLOSi S= {1,2,3,4,5,6,7,8,9,10} y A= {2,4,6,8,10}El complemento de A con respecto a S es el conjunto A`= {1,3,5,7,9}.Se dice que los conjuntos A y A' son mutuamente excluyentes.El complemento del conjunto universal S con respecto a si mismo es el conjunto Φ vacío.

49. INTERSECCION DE DOS CONJUNTOS VACIOSA∩B = { x|x € A y x € B}EJEMPLO:Si A= {1,2,3,4} y B= {3,4,5,6} A∩B= {3,4}Si A= {1,2,3,4} y B= {7,8,9} A∩B=Φ porque A y B no tienen ningún elemento común.A∩B representa un conjunto, mientras que n(A∩B) representa el numero de elementos del conjunto A∩B

50. Caso particular: A∩A`=Φ n(A∩A`)=0€ Ω|Φ∩∪

51. n(AUB) = n(A) + n(B)sABAUA`=S n(AUA`) = n(S)n(AUB)=n(A)+n(B) –n(AB)*ABBA

52. Probabilidad. Valor entre cero y uno, inclusive que describe la probabilidad relativa (oportunidad o casualidad) de que ocurra algún evento.

53. Probabilidad Es común que en la probabilidad aparezcan estos datos como 0.70, 0.27, 0.50, ……….ó tambien en forma fraccional como 7/10, 27/100, ½ ….. La probabilidad de 1 es algo que seguramente sucederá y 0 algo que seguramente no sucederá . Si un valor esta mas cerca del cero es probable que no suceda pero si esta mas cerca del uno es probable que este suceda.