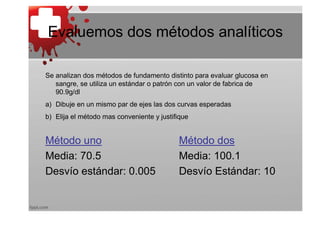
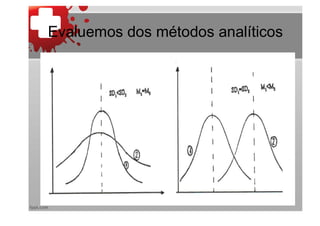
Este documento presenta conceptos básicos de estadística aplicada. Explica que la estadística se ocupa de recopilar y analizar datos para tomar decisiones. Define población, muestra, frecuencia, variable, media, mediana, varianza y desviación estándar. También introduce conceptos como distribución normal, estandarización y probabilidad. El objetivo es proporcionar las bases para realizar análisis estadísticos.

1. Conceptos básicos de
Estadística Aplicada
Mario Ariel Aranda

2. Estadísticas
La recopilación y la interpretación de los
datos obtenidos en un estudio es tarea de la
estadística, considerada como una rama de
la matemática. Las estadísticas (el resultado
de la aplicación de un algoritmo estadístico a un
grupo de datos) permiten la toma de decisiones
dentro del ámbito gubernamental, pero también
en el mundo de los negocios y el comercio.

3. Población
Es el conjunto de todos los elementos
que presentan una característica común
determinada, observable y medible. Por
ejemplo, si el elemento es una persona,
se puede estudiar las características
edad, peso, nacionalidad, sexo, etc.
Las características de la población se
resumen en valores llamados parámetros.

4. Muestra
La mayoría de los estudios estadísticos, se
realizan no sobre la población, sino sobre un
subconjunto o una parte de ella, llamado
muestra, partiendo del supuesto de que este
subconjunto presenta el mismo comportamiento
y características que la población. En general el
tamaño de la muestra es mucho menor al
tamaño de la población.

5. Población y Muestra

6. Frecuencia
• Se llama frecuencia a la cantidad de veces que
se repite un determinado valor de la variable.
• Frecuencia absoluta es el número de veces
que este valor aparece en el estudio. A mayor
tamaño de la muestra aumentará el tamaño de
la frecuencia absoluta.
• Frecuencia relativa (fi), es el cociente entre la
frecuencia absoluta y el tamaño de la muestra
(N). Es decir:

7. Problema
• Se detallan los valores de glucemia obtenidas
en una guardia del Hospital Gandulfo:
110-98-400-130-100-95-85-250-130-200-100-
110-300-130-550-99-130-110-120-89
Se pide:
a) analizar las frecuencias absolutas de cada
resultado
b) analizar las frecuencias absolutas de cada
resultado

8. Variable
Se llama variable a una característica que
se observa en una población o muestra, y
a la cual se desea estudiar.
La variable puede tomar diferentes valores
dependiendo de cada individuo.
Una variable se puede clasificar de la
siguiente manera.

9. Tipos de Variables
• Continua: son valores reales. Pueden
tomar cualquier valor dentro de un
intervalo. Ej. Peso, estatura, sueldos.
• Discreta: toma valores enteros. Ej. N° de
hijos de una familia, n° de alumnos de un
curso.

10. Variable-Población y Muestra
Se pretende averiguar cuantos Alumnos
de los que concurren al instituto de
Formación docencia viven en capital
federal
Población: todos los alumnos que
concurren al instituto
Muestra: alumnos de primer año-
Hemoterapia
Variable: los alumnos que viven en capital
federal

11. Sucesos-Espacio-Tiempo
Al extraer una carta de una baraja, lanzar una
moneda, tirar un dado, y en otros ejemplos análogos,
no podemos saber de antemano el resultado que se
va a obtener. Son experimentos aleatorios, aquellos
en los que no se puede predecir el resultado y de ellos
se trata aquí.
El conjunto de todos los posibles resultados de un
experimento aleatorio se llama espacio muestral, y
cada uno de esos posibles resultados es un suceso
elemental.

12. Definición
Un suceso es cualquier subconjunto del
espacio muestral, se verifica cuando
ocurre cualquiera de los sucesos
elementales que lo forman.

13. Ejemplo
• Se lanza un dado y se observa el
resultado obtenido:
• Espacio muestral: 1-2-3-4-5-6
• Suceso elemental: 1
• Suceso Vacío o imposible: 0-7-8….
• Suceso cierto: es aquel que siempre se
verifica, numero mayor que cero pero
menor que siete

14. Probabilidad
Se dice que un suceso A es más
probable que otro B si al realizar el
experimento muchas veces, A ocurre
significativamente más veces que B.
La probabilidad se mide entre 0
(probabilidad del suceso imposible) y 1 o
100% (probabilidad del suceso seguro).

15. Cuando en un experimento aleatorio todos los
sucesos elementales tienen la misma
probabilidad, equiprobables, para calcular la
probabilidad de un suceso cualquiera A, basta
contar y hacer el cociente entre el nº de sucesos
elementales que componen A (casos
favorables) y el nº de sucesos elementales
del espacio muestral (casos posibles) espacio.

16. Definiciones
• Experimento: se denomina experimento a un
proceso de observación o medición cualquiera.
Por ejemplo, lanzar 2 dados y anotar sus
resultados
• Espacio muestral: es el conjunto de todos los
posibles resultados de un experimento, el
espacio muestral del
lanzamiento de los 2 dados, son todos los pares
ordenados que se pueden formar con los 2
dados, es decir (1,1), (1,2), (1,3),..., (6,6). En
total 36 pares. Se designa por E.

17. Definiendo…
• Evento: es un subconjunto del espacio muestral.
Son elementos del espacio muestral que
cumplen con alguna condición dada. Por
ejemplo, el evento “que los dados sumen7”. Los
pares ordenados que cumplen esta condición
son: (2,5), (5,2), (3,4) y (4,3).
Los eventos se anotan con letras del abecedario
mayúsculas, ejemplo A, B,C,..., etc.

18. Definiendo…
• Probabilidad de un evento: Los eventos
que designaron con las letras A, B,C,...
tienen una probabilidad asociada a cada
uno de ellos y se designa como P(A),
P(B), P(C),..., etc.
• La probabilidad de un evento es un
número real no negativo y no superior a 1,
que mide la posibilidad que suceda dicho
evento

19. Propiedades
• Se cumple que:
• a) P(A) ≥ 0
• b) P(E) =1
• c) 0 ≤ P(A) ≤ 1
• d) P(A) + P(A’)=1 donde A’ es el
complemento de A.
P(A) = Nº de casos posibles del evento A
Nº de casos totales

20. Ejemplo…
• Cual es la probabilidad de que si tiro la
moneda sale" cara ”?

21. Definición
• Eventos mutuamente excluyentes: dos o
más eventos son mutuamente
Excluyentes si y solo si no pueden ocurrir
al mismo tiempo, es decir, la ocurrencia
de un evento A impide automáticamente la
ocurrencia de un evento B.
Ej.: Al extraer una carta de un naipe de 52 cartas. Sea A = sacar un
as. B = sacar un rey.

22. Desvío estándar
• La desviación estándar (σ) mide cuánto se
separan los datos.
• La fórmula: es la raíz cuadrada de
la varianza. Así que, "¿qué es la
varianza?"

23. Varianza
 la varianza ( es el cuadrado de la desviación
estándar: σ2)
 Es la media de las diferencias con la
media elevadas al cuadrado.
En otras palabras, sigue estos pasos:
1. Calcula la media (el promedio de los
números)
2. Ahora, por cada número resta la media y
eleva el resultado al cuadrado (la diferencia
elevada al cuadrado).
3. Ahora calcula la media de esas diferencias al
cuadrado. (¿Por qué al cuadrado?)

24. Varianza
• Esta medida nos permite identificar la
diferencia promedio que hay entre cada
uno de los valores respecto a su punto
central (Media ).

25. Media
• La media aritmética es el promedio de un
conjunto de números, a1, a2, a3, . . ., an,
obtenida sumando todos los números y
dividiéndola entre n. (media aritmética) =
(a1+a2+a3+ . . . +an)/n

26. Formula del desvío estándar

27. Mediana
• Es el valor medio en un conjunto de valores ordenados.
• Sean los datos de una muestra ordenada en orden creciente y
designando la mediana como , distinguimos dos casos:
• a) Si n es impar, la mediana es el valor que ocupa la posición una
vez que los datos han sido ordenados (en orden creciente o
decreciente), porque éste es el valor central.
• b) Si n es par, la mediana es la media aritmética de los dos valores
centrales.

28. Problema
• Los datos representan la edad de los
miembros de un grupo de niños que
asisten a un servicio de pediatría en el
mes de enero del 2013.
4, 1, 11, 13, 2, 7 , 12, 5, 8,
Hallar :
a) La media Respuestas:
b) La Mediana Media: 7 años
c) El desvío estándar Mediana: 7 años
Desvío: 4,36 años

29. Problema
• Las notas de inglés de una clase de 40
alumnos han sido las siguientes:
1 7 9 2 5 4 4 3 7 8
4 5 6 7 6 4 3 1 5 9
2 6 4 6 5 2 2 8 3 6
4 5 2 4 3 5 6 5 2 4
• Calcular: frecuencia, Media, mediana,
Varianza, desvío estándar
• Cual es la probabilidad de obtener un 7?

30. Varianza-Ejemplo
• Hallar la desviación media, la varianza y
la desviación estandar de la series de
números siguientes:
a) 2, 3, 6, 8, 11.
b) 12, 6, 7, 3, 15, 10, 18, 5.
Respuestas: a) Media=6, Var=10.8, σ=3.28
b) Media=9.7, Var=23.75, σ=4.87

31. Coeficiente de Variación
El Coeficiente de variación (CV) es una
medida de la dispersión relativa de un
conjunto de datos, que se obtiene
dividiendo la desviación estándar del
conjunto entre su media aritmética y se
expresa generalmente en términos
porcentuales.

32. Coeficiente de Variación/ Desvío
estándar
• CV: • DS:
El coeficiente de variación es La desviación estándar da una
una medida que indica, qué medida de lo que, en
tan dispersos o separados promedio, se aleja cada dato
están los datos, unos con de la media.
respecto a otros. Un CV
cercano a cero indica que los
datos están muy juntos (o son
muy similares), mientras que
un CV muy grande (cercano a
100% o a 1, o mayor a estos
valores) indica que los datos
están muy dispersos o son
muy diversos.

33. Problema
• Dos Contadores hematológicos
utilizados durante un día registran sobre
las mismas muestras los siguientes
valores de GR
Equipo 1: x(106) 4,5-5,0-3,5-5,3-4,3-3,8-5,2
Equipo 2: x(106) 3,9-4,8-4,2-4,2-4,8-3,3-4,6
Se pide:
a) Analizar el CV para ambos contadores
b) Cual seria el mas apto? fundamente

34. Distribución Normal
La mas utilizada de las distribuciones continuas
es la distribución normal. Esta distribución con
un gráfico como campana se centra en el valor
promedio, denominado μ y su dispersión
respecto a él, se denomina σ, llamada
desviación estándar.
La función normal describe de forma aproximada
muchos fenómenos que suceden en la
naturaleza tales como la estatura de las
personas, el coeficiente intelectual en los niños,
etc.

35. Gráficos
Área bajo la curva = 1

36. Gráficos

37. • Una propiedad importante de la
distribución normal, es que cualquier
función lineal de una variable aleatoria
distribuida normal, también tiene
distribución normal, es decir, si x ∼ N.
Entonces y = ax + b, también y ∼ N.
Se denota x ∼ N (μ, σ2)
Si y = ax + b ⇒ y ∼ N(aμ + b; a2σ2)

38. Puede existir un nº infinito de
distribuciones normales posibles, cada
una con su propia media y su desviación
estándar ya que obviamente no se puede
analizar un nº tan grande de posibilidades,
es necesario convertir todas estas
distribuciones normales a la forma
estándar. Esta conversión se hace a
través de la variable Z.

39. Estandarización
Donde Z es una variable aleatoria normal con media cero
X −μ y varianza 1.
Z= σ La variable Z se define como el nº de desviaciones
estándar a las una observación está de la media.
Ej.: Un curso tiene un promedio de 1,75 m de estatura, con
desviación de 2 m.
Si un alumno tiene una estatura de 1.8 m entonces
Z = 1.80 – 1.75 Z= 0.93
2
esto quiere decir que su estatura esta a 0.93 desviación estándar
por sobre de la media

40. Estandarización
• Estandarizar una distribución normal
permite determinar mas fácilmente la
probabilidad de que ocurra cierto evento.
• La probabilidad de un evento esta
relacionado con el área bajo la curva
normal estándar en el punto Z.

42. Otro ejemplo
• La edad de los estudiantes de Técnico en
hemoterapia de la capital federal sigue
una distribución normal con x ∼ N (25, 10)
• Cual es la probabilidad de que encuentre
a un alumno con 40 años?
Z=40 – 25 = 1.5
10
La probabilidad es el área bajo
la curva desde Z=1.5 hacia la
izquierda

43. Una curva normal queda completamente
determinada una vez que se especifica μ y
σ2

44. Formas de los gráficos
Este gráfico muestra la curva normal manteniendo la misma
variabilidad pero distinta media

45. Formas de los gráficos
A diferencia del anterior se observan distinta curvas
normales con la misma media y diferentes variabilidades.
Mientras más alta es la variabilidad la curva se aplana.

46. Otras formas de curvas

47. Propiedades
• La simetría se da con
la recta vertical x = μ
• El 99,73% de las
observaciones
quedan incluidas en
el intervalo μ - 3σ, μ +
3σ

48. • P(μ − 3σ < x < μ + 3σ ) = 0,9973
• P(μ − 2σ < x < μ + 2σ ) = 0.9594
• P(μ − σ < x < μ + σ ) = 0.6845

49. Utilidad
• El laboratorio debe
realizarla verificación • Linealidad.
de los métodos y • Precisión.
evidenciar si cumplen • Veracidad.
con las características
• Incertidumbre.
de desempeño en las
condiciones del
laboratorio.

50. Linealidad
Evaluar el intervalo
analítico del método
en el laboratorio.
• El comportamiento
lineal.
• La verificación debe
tomar en cuenta los
puntos de decisión
clínica.

51. Exactitud
Expresa la cercanía entre el
valor que es aceptado, sea
como un
valor convencional verdadero
(material de referencia interno
de la firma), sea como un valor
de
referencia aceptado (material
de referencia certificado o
estándar de una farmacopea)
y el valor
encontrado (valor promedio)
obtenido al aplicar el
procedimiento de análisis un
cierto número de
veces.(Sistematico).

52. Precisión
Expresa la cercanía de
coincidencia (grado de
dispersión) entre una
serie de mediciones
obtenidas de múltiples
muestreos de una misma
muestra homogénea bajo
condiciones establecidas.

53. Resumiendo

54. Evaluemos dos métodos analíticos
Se analizan dos métodos de fundamento distinto para evaluar glucosa en
sangre, se utiliza un estándar o patrón con un valor de fabrica de
90.9g/dl
a) Dibuje en un mismo par de ejes las dos curvas esperadas
b) Elija el método mas conveniente y justifique
Método uno Método dos
Media: 70.5 Media: 100.1
Desvío estándar: 0.005 Desvío Estándar: 10

55. Evaluemos dos métodos analíticos